深海采矿系统水平软管水力输送阻力损失规律研究

曹　斌，刘金炜，夏建新

（中央民族大学　环境系，北京　100081）

深海采矿系统水平软管水力输送阻力损失规律研究

曹斌，刘金炜，夏建新

（中央民族大学环境系，北京100081）

目前公认的深海采矿系统是利用管道水力将深海底矿石提升到海面采矿船上。由于受海底破碎条件和废水排放环境要求，输送的深海矿石粒径较粗。粗颗粒具有极易沉积的特点，输送参数也较难确定。通过自行设计的管道水力输送模拟系统，研究了不同浓度、粒径、速度条件下粗颗粒在水平管道中的运动状态及阻力损失的变化规律。研究结果表明：（1）随固液两相流流速的增大，水力坡度呈现规律性变化，且阻力损失的变化规律与粗颗粒运动状态存在一定的关系；（2）通过引入管道附加损失与福氏数，建立了颗粒运动状态与阻力损失之间的定量关系，提出了粗颗粒在水平管道水力输送条件下流态分区的判定标准；（3）分析了管道附加损失的影响因素，提出了管道附加损失的计算公式。研究结果为粗颗粒管道水力输送系统参数设计提供依据。

粗颗粒；水平软管；阻力损失

深海蕴藏着多金属结核、硫化物等丰富的矿产资源，目前开采这些资源可行的方法是利用管道水力输送系统将深海底矿石提升到海面采矿船上。该系统由扬矿硬管、扬矿泵、中间仓、柔性软管等多环节组成［1］。深海矿石输送具有输送颗粒粗、输送距离长、输送条件复杂等特点。为适应海底地形起伏变化和实现按照回采路径采矿，在主提升管道与海底集矿机之间必须有一段柔性软管，该段输送管道浮在海水中，随着集矿机与主管相对位置的变化而出现不同的形态，甚至可能出现接近水平的形态，这种形态不利于粗颗粒矿石的输送［2-4］。同时，受海底破碎条件和废水排放环境要求，输送的深海矿石粒径较粗，粗颗粒与液相无法形成均质浆体，不仅阻力特性复杂，而且容易堵塞管道，可能造成严重的工程事故［1，5-7］。因此，研究粗颗粒在水平软管中输送的阻力损失变化规律尤为重要。

诸多学者针对固液两相流阻力特性进行了研究，如Engelmann和Asakura分别采用试验研究和数值模拟的方法对粗颗粒在垂直管水力提升阻力特性进行了研究［8-9］；杜兰德、PavelVlasak等［10-11］研究了粗颗粒附加损失与福氏数的关系；瓦斯普、费祥俊等［12-13］对煤炭和河沙等细颗粒物料管道水力输送阻力损失进行了大量的试验研究和系统分析等。但对粗颗粒在水平管道输送的研究较少，尤其是粗颗粒运动状态与阻力损失变化规律的定量关系尚不清楚，不能为深海采矿管道输送系统设计提供技术依据。

本文拟利用试验，分析不同粒径、体积浓度和输送速度条件下阻力损失的变化规律，通过引入管道附加损失和福氏数，构建粗颗粒运动状态与阻力损失的定量关系，提出粗颗粒在管道中的附加阻力损失计算公式。

1　试验系统及方法

为模拟柔性软管在深海采矿系统的工作环境，并建立了粗颗粒管道水力输送试验系统，如图1所示。该系统由管道输送系统、动力控制系统、试验测量系统等三部分组成。管道直径50 mm，长度20 m。采用星形叶轮式给料机给料，在固液两相流经固液分离滤网过滤后，物料直接进入给料机料箱，物料不需要过泵，有效地避免了物料破碎；采用清水泵作为流体输送动力，给料机和涡流泵均采用变频调速器可以进行无级调速。在水平管中部安装一段长2 m透明的有机玻璃管，以便于用高速摄影机记录颗粒的运动状态及其速度变化。

图1　管道水力输送试验系统示意图

试验液相为清水，固相以天然石英砂模拟深海矿石，试验物料选取1.5 mm，2.5 mm，3.5 mm以及4.5 mm四组粒径，物料体积浓度设定为10%，15%，20%和25%四组。试验时，先启动泵，再将同一组粒径的物料按照一定浓度均匀投入加料仓，待系统运行稳定后，利用高速摄影机记录颗粒运动状态，测量粗颗粒不同运动状态的高度，以不同运动状态颗粒面积占管道截面面积的百分比作为判定粗颗粒主要运动状态的依据，如图2所示。利用电子压差计测量不同粒径、体积浓度和输送速度条件下阻力损失的变化。输送速度和物料浓度通过取样标定得到。

图2　管道中不同运动状态颗粒比例计算模式

2　矿石在管道中运动状态与输送阻力变化

2.1矿石在水平管道中的运动状态

通过图2所示的方法，通过计算不同运动状态矿石颗粒面积占管道截面积的百分比得到矿石颗粒运动状态示意图，如图3所示。

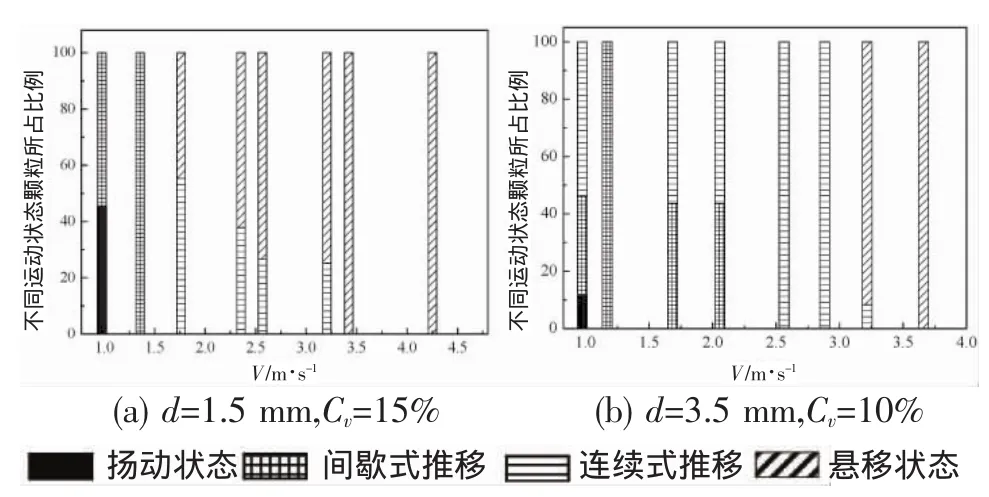
图3　不同运动状态颗粒的百分比

在水平管道中，随着水流强度加大，矿石颗粒出现四种运动状态：扬动、间歇式推移、连续式推移、悬移，且同一断面中不同位置的颗粒会呈现不同的运动状态。

（1）扬动状态。随着水流速度加大，矿石颗粒所受到的拖曳力FD也随之增大，当FD＞f（G'-FL）时，矿石颗粒开始向前滚动，出现扬动。其中FD表示拖曳力，FL表示上举力，G'表示颗粒在水中的有效重量，f表示静摩擦系数。处在扬动状态的颗粒，其速度远远小于水流速度，运动状态不稳定，停滞与滚动交替出现。

（2）间歇式推移。当水流速度继续增加，拖曳力FD也随之增大到满足FD＞G2'，上举力FL=G1'时，更深层的矿石颗粒物开始运动，其运动状态表现为滚动和滑动状态同时出现，此时为间歇式推移状态。间歇式推移呈现出周期性运动的特点，起初底层的矿石颗粒始终与管壁保持接触且静止，表层的矿石颗粒不断堆积，而堆积会导致过流断面逐渐减小，局部水流流速逐渐增加，增加到一定程度后，整个截面的矿石颗粒被水流一起冲走，从而出现“沙丘”式的运动状态。其中G1'、G2'分别表示矿石颗粒水下所受重力的分力。

（3）连续式推移。当流速继续增加，拖曳力FD也随之增大，各层矿石颗粒之间开始形成稳定的运动状态，逐渐达到连续式推移状态。处在连续式推移状态的矿石颗粒，各层之间运动近乎于平行，运动只能成层运动，此时矿石颗粒的运动速度从上至下依次递减，颗粒之间的不断碰撞导致矿石颗粒之间摩擦阻力增加，因此此时水流存在较大坡降维持颗粒运动。

（4）悬移。当水流速度增加到使矿石颗粒的受力满足FL＞G1'时，颗粒物开始脱离床面，悬浮在液相中，出现悬移状态。悬移状态下，矿石颗粒的运动特点为所有颗粒物均悬浮在液相中，随水流运动，矿石颗粒在水平管道中的运动速度与水流速度基本一致。

2.2矿石输送阻力变化

本文绘制阻力损失随流速的变化的趋势，并利用虚线将矿石颗粒运动状态进行分区，如图4所示。

图4　水力坡度随流速增大的变化规律

由图4可知，对于不同粒径，阻力损失随着平均流速的增加呈现先减小后增加的趋势，且随流速增大，各曲线逐渐趋近于清水的水力坡度。

扬动的阻力损失主要来自于液相与颗粒间的摩擦力和通过颗粒间隙产生的渗流导致的能量损失；间歇式推移的阻力损失主要来源于颗粒间的摩擦、颗粒与管壁的摩擦力和部分颗粒与水流产生的摩擦。较扬动状态而言，随水流强度的增加，由于颗粒离散度增加，使得渗流导致的能量损失减小，因此，固液两相流的能量损失逐渐减小并达到最小值；连续式推移的阻力损失主要来自于颗粒间的摩擦力、颗粒与管壁的摩擦力、水流与颗粒间的摩擦力以及通过颗粒间隙而产生的渗流导致的能量损失，因此随着流速的增加，阻力损失从最小值开始逐渐增加；悬移状态是在大尺度紊动的作用下形成的，悬移质的能量来源于水流的紊动动能，其之所以能够悬浮，是因为其从水流的紊动动能中取出一部分能量，其支持力为紊动漩涡，在该运动状态下，阻力损失值较大，且随流速增加阻力损失不断增加。

综上，矿石颗粒在水平管道中处于扬动状态时，其阻力损失较大，产生不必要的能量消耗，且输送量少，效率低，而间歇式推移是一种不稳定的运动状态，没有实际意义；而使矿石颗粒完全处于悬移状态又需要较高流速，经济损失必然上升，因此，可以定性判断连续式推移是矿石颗粒在水平管道中运输的最佳输送形式。

3　管道输送附加阻力影响因素及计算式

为分析矿石颗粒运动状态与阻力损失的定量关系，本文引入了非均质流管道附加损失（im-i0）/（Cv× i0）表征阻力损失的大小（式中im，i0分别表示浆体和清水的水力坡度，Cv表示颗粒的体积浓度）。根据已有研究成果，管道附加损失的主要影响因素有水流速度、颗粒物料粒径，因此又引入两个参数，即：管道流动福氏数Fr=v2/gD（其中，v表示浆体的平均流速，g表示重力加速度，取9.8 m/s2，D表示管道直径）以及粒径与管径的比值d/D（式中d表示颗粒粒径）。

3.1附加阻力与固液两相流速的关系

为分析管道附加损失与流速之间的关系，得到管道附加损失随福氏数变化的曲线，如图5所示。

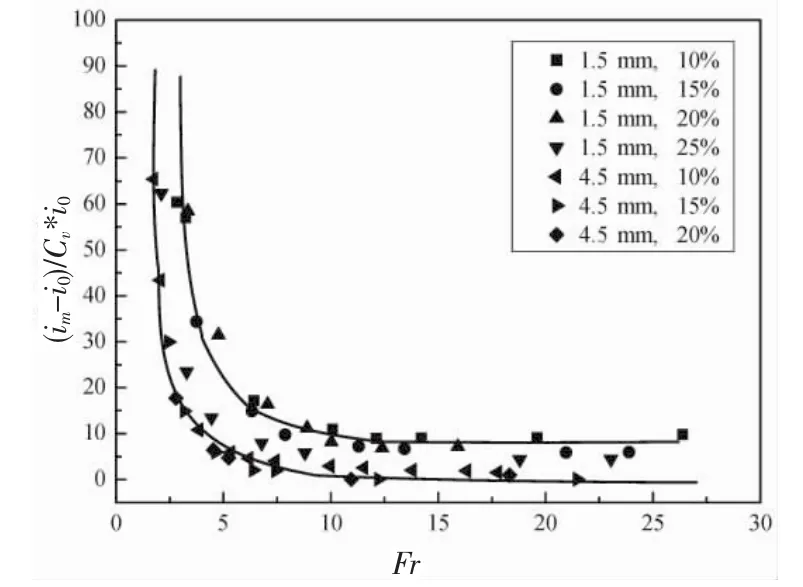
图5　管道附加损失与福氏数间的关系

根据图5对管道附加损失和Fr的关系进行分析可知：

当（im-i0）/（Cv×i0）＞45时，矿石颗粒以扬动和间歇式推移为主，此时（im-i0）/（Cv×i0）的变化随v2/gD的增加急剧减小。颗粒出现间歇式推移时，固液两相流流速低，在该运动状态下，矿石颗粒处于密实接触状态，此时颗粒间的相互摩擦作用力以及渗流起到相当大的影响，因此固液两相流平均流速越小，颗粒间接触越频繁，管道附加能量损失越大。

当10≤（im-i0）/（Cv×i0）≤45时，矿石颗粒以连续式推移为主，此时（im-i0）/（Cv×i0）的变化率随v2/gD的增加逐渐减小。连续式推移是矿石粗颗粒在水平管道中较高流速条件下的运动状态，此时管道内的能量损失主要包括液相与管壁的摩擦力，颗粒与管壁的摩擦力，颗粒间的摩擦力以及液相通过颗粒间隙产生的渗流导致的能量损失。矿石颗粒进行连续式推移时，随着流速的增加，矿石颗粒由密实接触状态转变为松散状态，颗粒间的摩擦力和液相通过颗粒间隙产生的渗流导致的能量损失越小，然而，液相与管壁的摩擦力，颗粒与管壁的摩擦力逐渐增加，且当流速较高时，颗粒可从清水紊动动能中获取一定的能量，趋向于悬移。因此，在连续式推移状态下，管道附加损失随着流速增加呈现先慢后快的趋势。

当（im-i0）/（Cv×i0）＜10时，矿石颗粒以悬移为主，此时（im-i0）/（Cv×i0）的变化随v2/gD的增加变化很小。颗粒出现悬移时，固液两相流流速高，此时管道内的能量损失主要是清水与管壁的摩擦力和颗粒间离散作用力起主要作用。在该运动状态下，矿石颗粒从清水紊动动能中获取能量，使得颗粒悬浮在清水之中，且流速越高，颗粒获得的紊动动能越多，越容易悬浮，越接近清水的流速，而此时由于颗粒悬浮在清水中，颗粒间间隙远大于颗粒粒径，因此在悬移状态下，管道附加损失减小到一定值且接近于这个定值。

综上，利用管道附加损失与福氏数建立了管道阻力损失与矿石颗粒运动状态间的定量关系，因此可将水平管道附加损失作为矿石颗粒在水平管道水力输送条件下流态分区的判定标准。

3.2附加阻力与颗粒粒径间的关系

管道附加损失与输送颗粒粒径大小有关，为分析管道附加损失与颗粒粒径之间的定量关系，得到管道附加损失随d/D变化的曲线，如图6所示。

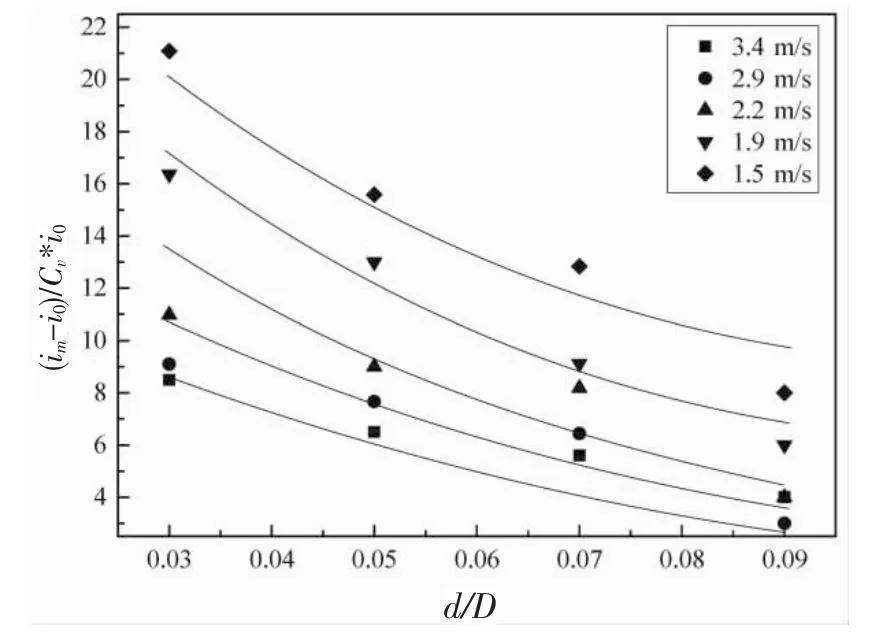
图6　管道附加损失与d/D的关系（Cv=10%）

根据图6对管道附加损失和粒径管径比d/D的关系进行分析，获得两者之间关系如下:

在一定的体积浓度下，随着粒径的增加，管道附加损失呈递减的趋势。分析其原因是由于在体积浓度相同的情况下，颗粒粒径越小，其数量越多，则颗粒摩擦、碰撞的概率越大，固相能量耗散越大。同时，在体积浓度和颗粒粒径一定的条件下，平均流速越低，其管道附加损失越大，这主要是由于在低流速条件下，颗粒主要以扬动和间歇式推移的形式存在，颗粒间摩擦、碰撞作用会使得能量耗散增加，而随着平均流速的增加，颗粒可从液相紊动动能中获取更多的能量使颗粒出现由推移质向悬移质运动的趋势，此时颗粒间的间距增大，其碰撞、摩擦概率以及颗粒与管壁的摩擦降低，从而使得能量耗散减小。

3.3附加阻力与颗粒密度间的关系

颗粒密度是物料固有的物理性质，决定了颗粒在水中的沉降性能及运动能力，从而影响固液两相流的阻力损失。本文结合已有研究成果［14］，采用无量纲数s，其中s=ρs/ρw（式中ρs为粗颗粒的密度，ρw为清水的密度），由于颗粒尺寸对于密度对阻力损失的影响不大，以此确定管道附加损失与密度的关系如式（3）所示：

3.4管道附加阻力计算公式

在上述管道附加阻力影响因素分析基础上，采用量纲分析法，结合式（1）～式（3），得到管道附加阻力的计算式：

式中：K由试验数据拟合，与颗粒形状、粒径不均匀程度等因素等相关的综合系数有关，取值范围为50～80之间。

图7给出了基于式（4）的管道附加损失测量值与计算值的结果比较。经分析，误差范围基本在15%以内。

图7　管道附加损失计算值与实测值比较

4　结论

管道中依次出现扬动、间歇式推移、连续式推移、悬移，且随着水流流速的增加，阻力损失呈现先减小后增加的趋势，且矿石颗粒运动状态与阻力损失存在一定的关系；

（2）引入非均质流管道附加损失与福氏数，提出了矿石颗粒在水平管道水力输送条件下流态分区的定量判定标准，构建了沿程阻力损失与颗粒运动状态间的定量关系；

（3）分析了管道附加损失的影响因素，分析管道附加损失与福氏数、颗粒与管径比以及颗粒比重之间的关系，提出了管道附加损失与输送速度、颗粒粒径、颗粒比重的定量表达式，得到管道附加损失的计算公式。

（1）随着水流流速由小到大，矿石颗粒在水平

［1］阳宁，周知进，唐达生，等.粗颗粒水下管道输送系统振动的实验研究［J］.海洋工程，2014，32（3）：104-109.

［2］徐海良，何清华.深海采矿输送管道内流体对管道的作用力分析［J］.矿业研究与开发，2004，24（6）：46-49.

［3］艾志久，刘锋，赵欣，等.海洋管道浮拖过程力学分析［J］.海洋工程，2007，25（4）：88-91.

［4］金咸定.海洋管道工程的若干力学问题［J］.海洋工程，1984，4：23-30.

［5］赵利安，许振良.倾斜管道水力坡度的研究［J］.辽宁工程技术大学学报，2003，22（增刊）：15-17.

［6］胡寿根，秦宏波，白晓宁，等.固体物料管道水力输送的阻力特性［J］.机械工程学报，2002，38（10）：12-16.

［7］李畅，夏建新.深海矿产资源开发水力提升系统参数预测及优化［J］.矿冶工程，2007，4：23-27.

［8］Engelmann H E.VerticalHydraulic LiftingofLarge-Size Particles—AContribution toMarine Mining［J］.Offshore TechnologyConference，1978.

［9］Asakura K，Asari T，Nakajima I.Simulation of Solid-Liquid Flows in Vertical Pipe by a Collision Model［J］.Powder Technology，1997，145（4）：201-209.

［10］Durand R.The Hydraulic Transportation ofCoal and Other Materials in Pipes［J］.CollogofNational Coal Board，London，1952.

［11］Pavel Vlasak，Bohus Kysela，Zdenek Chara.Flow Structure of Coarse-Grained Slurry in a Horizontal Pipe［J］.J Hydrol Hydromech，2012，60（2）：115-124.

［12］瓦斯普，等.固体物料的浆体管道输送［M］.黄河水利委员会译.北京：水利电力出版社，1980.

［13］费俊祥.浆体与粒状物料输送水力学［M］.北京：清华大学出版社，1994.

［14］叶坚，夏建新，Malczewska Beata.水平管道水力输送粗粒物料的阻力损失研究［J］.金属矿山，2011，7：12-18.

Study on the Resistance Loss of Hydraulic Transport in the Horizontal Pipeline of the Deep Sea Mining System

CAO Bin，LIU Jin-wei，XIA Jian-xin
Department of Environment，Minzu University of China，Beijing 100081，China

This paper studies the motion statements and resistance loss variations of coarse grains in pipelines under different conditions like concentration，diameter and transportation velocity through pipeline hydraulic transportation experiments，and proposes additional loss formula of coarse grains that are safely transported.The main conclusions are as the following:（1）According to the transport velocity from low to high，the hydraulic slope represents regular variation，and the motion statements of coarse grains can be divided into four types:starting movement state，contacting movement state，loading movement state，and suspended movement state.The loading movement state has the lowest resistance loss，which can be qualitatively presumed as the main state for coarse grain movement；（2）This paper introduces two parameters:additional losses and Reynolds，which help to build the quantitative relationship between particle movements and resistance loss，and propose the judgement standard for different states of motion in horizontal pipelines.（3）By analyzing the factors affecting additional losses and building the relations between them，this paper proposes the formula of additional losses.

coarse grain；horizontal pipeline；resistance loss

P744

A

1003-2029（2016）04-0114-06

10.3969/j.issn.1003-2029.2016.04.021

2015-12-05

国家自然科学基金资助项目（51209238，51339008，51434002）

曹斌（1981-），男，博士，讲师，主要从事管道水力输沙研究。E-mail：caobin_erli@163.com