一种用于大场景双目视觉系统摄像机的标定方法
王 剑,王宇胜,刘 峰,李清嘉
(1.中国民航大学a.电子信息工程学院;b.中欧航空工程师学院,天津 300300;2.天津大学精密仪器与光电子工程学院,天津 300072)
一种用于大场景双目视觉系统摄像机的标定方法
王剑1a,王宇胜1a,刘峰2,李清嘉1b
(1.中国民航大学a.电子信息工程学院;b.中欧航空工程师学院,天津300300;2.天津大学精密仪器与光电子工程学院,天津300072)
基于相机成像的针孔模型,通过建立世界坐标系、摄像机坐标系和图像坐标系之间的数学关系,理论上推导了摄像机相关参数显式的表达式,并在此基础上探究了参数与坐标的关系。通过获取实验数据验证了各参数标定结果的准确性。利用标定结果,根据图像坐标系目标图像坐标(u,v)与其对应的大地坐标值(Xw,Zw)之间的关系计算了各个目标的大地坐标,并将计算结果与GPS计算的目标坐标、参数参考值计算的坐标结果相比较,在误差允许的范围内,提出了一种双目视觉条件下的摄像机标定方法。
双目视觉系统;针孔模型;摄像机标定;目标定位;世界坐标系;图像坐标系
image coordinate system
民用机场客流量逐年增加,使机场场面监视的压力与日俱增。现有监视设备造价高、维护成本也较高,且系统存在各自的不足;除了传统的场面雷达、ADS-B和MLAT等监视手段外,需要寻找新的途径来实现机场场面的监视,以满足下一代交通管控[1]的发展。计算机双目视觉系统以其非接触性、速度快和高精度的特点在诸多方面发挥了重要作用[2]。双目视觉的基本任务之一就是通过获取图像中目标的坐标信息来实现世界坐标系中对应目标的准确定位。建立数学模型后,为了实现目标更加准确的定位,首先获取摄像机的参数是不可或缺的一步,即摄像机的标定,标定结果直接影响着坐标的误差[3]大小。文献[4]提出了一种大视场条件下的标定方法;此外文献[2,5~7]中介绍了多种标定的方法,但主要是针对摄像机的镜头畸变实现参数的求解。本文主要是针对大场景条件下提出的一种基于针孔模型计算相机相关参数的方法,并进行了验证。
本文首先推导需标定参数的表达式,分析了这些参数对目标坐标定位误差的影响,通过实验数据进行求解。利用这些参数的参考值和参数的标定值分别求解目标的坐标,与差分GPS(DGPS)计算的坐标结果相比较,验证了标定参数的正确性,因此,可利用本文方法求解摄像机的参数。
1 参数求解及坐标关系
1.1参数求解
根据摄像机针孔成像模型及摄像机图像坐标系、摄像机物理坐标系与大地坐标系的对应关系,可得出如下方程组[8-9]
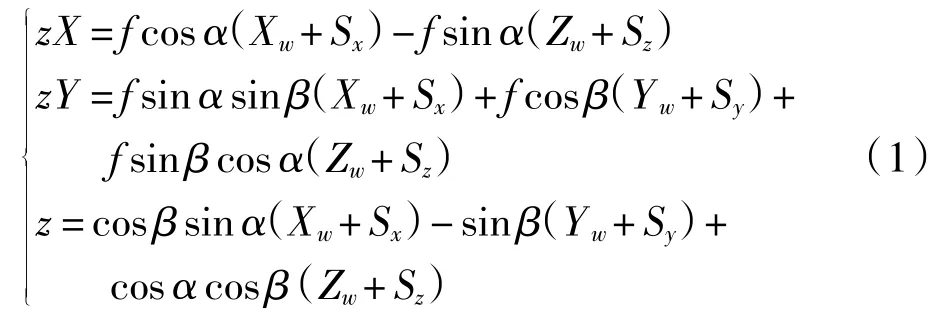
其中:α为相机光轴自转角;β为相机俯仰角;(Xw,Zw)为目标在当前世界坐标系中的大地坐标;(Sx,Sy,Sz)为相机在当前世界坐标系中的大地坐标;(X,Y)为目标的物理坐标;f为相机焦距。
将方程组(1)中第1个和第2个方程左右两端相除,可消去参数f和z,得到如下关系式
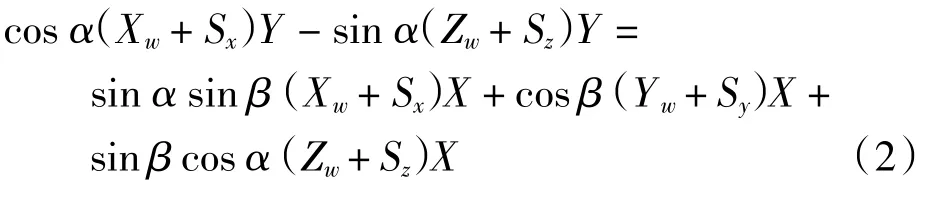
为方便求解,令

则式(2)可写成如下形式
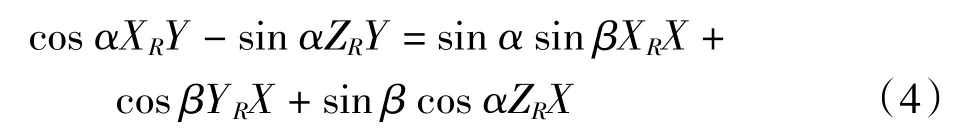
假设场景内存在3个靶标,其世界坐标分别表示为 P1(Xw1,Yw1,Zw1)、P2(Xw2,Yw2,Zw2)、P3(Xw3,Yw3,Zw3),3个靶标对应的图像坐标分别表示为(X1,Y1)、(X2,Y2)、(X3,Y3),则3个靶标都可以按照式(3)写出,下标数字表示对应的靶标,然后将其代入式(4),可写成如下方程组
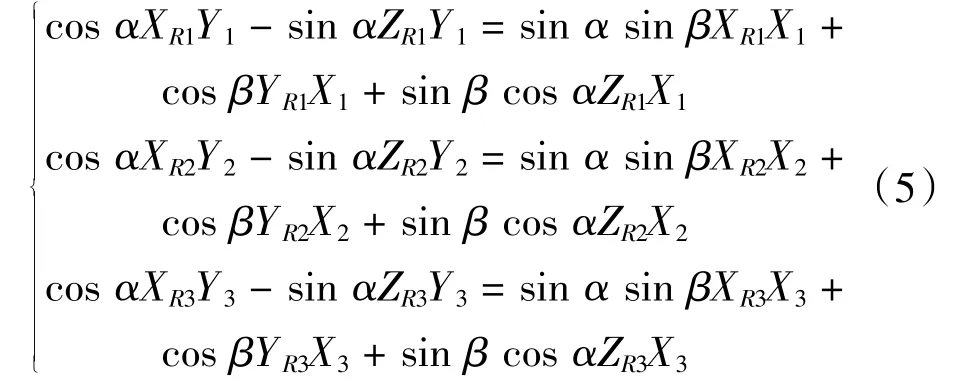
将方程组(5)中第1个方程分别与第2个方程、第3个方程左右两端相除,可得到如下方程组

其中
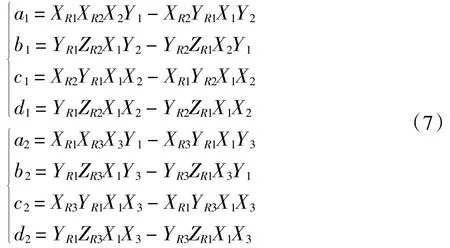
参数β求解如下

参数α、f求解如下
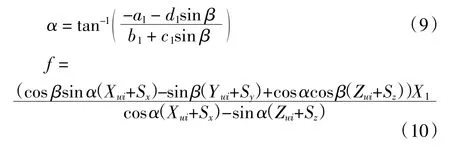
得出3个参数的显式表达式,便于探讨其与坐标的关系和实验参数验证。
1.2参数与坐标的关系
在进行标定前,有必要说明参数与坐标之间的关系,对于双目视觉系统,测站相机焦距与坐标的关系如图1所示。
fl、fr分别表示2个相机的焦距,(Xw,Zw)表示靶标的大地坐标。从图1可以看出,当左右站焦距分别从0.023 8 m变化到0.025 8 m和0.024 3 m到0.026 30 m时,Xw值的变化范围为(-44.081 2,-40.885 8)m,Zw值的变化范围是(-23.252 9,-11.535 8)m,如果焦距不标定或标定结果偏差较大,则坐标偏差较大。显然,如果左右站标定偏大或偏小,焦距对坐标的影响是很显著的。
同样的,参数α与世界坐标的关系如图2所示。
这里,α1和α2分别表示左右站的自转角,二者的变化范围分别是(3.394 665,3.412 118)rad和(2.861 268,2.878 721)rad,相应地,Xw和Zw的变化范围分别为(-43.603 98,-40.908 0)m和(-27.393 7,-6.508 9)m,不难看出,Zw的变化也是较为明显。由于参数对目标坐标的影响较明显,所以,参数求解的准确与否对于求解精确的目标坐标有重要的影响。

图1 坐标与焦距f的关系Fig.1 Relationship between coordinates and focal length f

图2 坐标与α的关系Fig.2 Relationship between coordinates and α
β与坐标的关系如图3所示。

图3 坐标与β的关系Fig.3 Relationship between coordinates and β
从这里可以看出,相对于图1和图2,当左右站β的变化范围从1°~10°时,对坐标的影响相对较小。
从上述坐标与参数α、β、f的关系图来看,参数标定的准确与否对坐标的影响较大,尤其是参数自转角α和焦距f。所以,为使目标定位误差更小,参数的标定结果显得尤为重要。
2 实验及标定结果
2.1实验简介
该实验需要的2个相机可被称为左站和右站,左右站2个网络相机的光轴汇聚于一点,并且左右站的相机适合被放置在当前所建世界坐标系Z轴的两侧。本实验中参数β为0°或者一个较小的角度;左右站通过光纤或微波传输图像到上位机,上位机对其进行相关的处理如获取目标坐标参数,求解相关参数。现场示意图和实验相关设备如图4和图5所示。
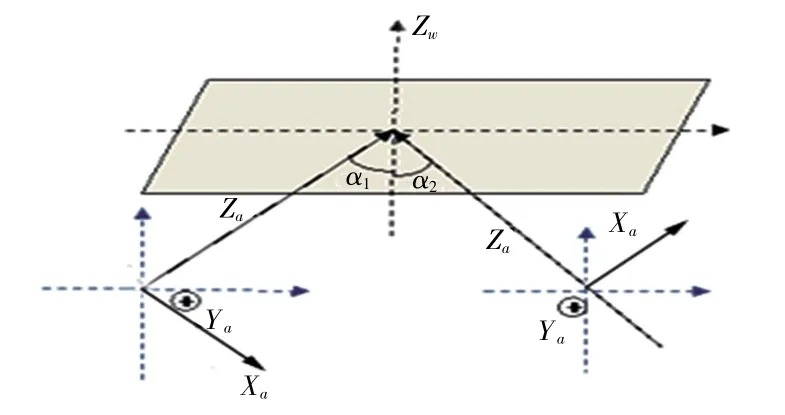
图4 实验示意图Fig.4 Experimental schematic diagram
2.2实验数据
相机内部参数:图像像素dx=dy=0.007 4 mm,图像坐标系中双目视觉2个相机光轴交汇点的像素坐标(u0,v0)=(800,200)。

图5 实验设备Fig.5 Experimental set
相机外部参数:S1、S2分别表示左右测站与原点的距离,S1=345.204 6 m,S2=328.580 0 m;θ1、θ2表示测站和中心点连线与正北方向的夹角,这些数据均可通过差分GPS(DGPS)获取,θ1=160.3395°,θ2=129.7745°。其中,由参数θ1、θ2可计算出左右测站自转角分别为α1=15.000 0°,α2=-16.565 0°。
实验数据如表1所示。
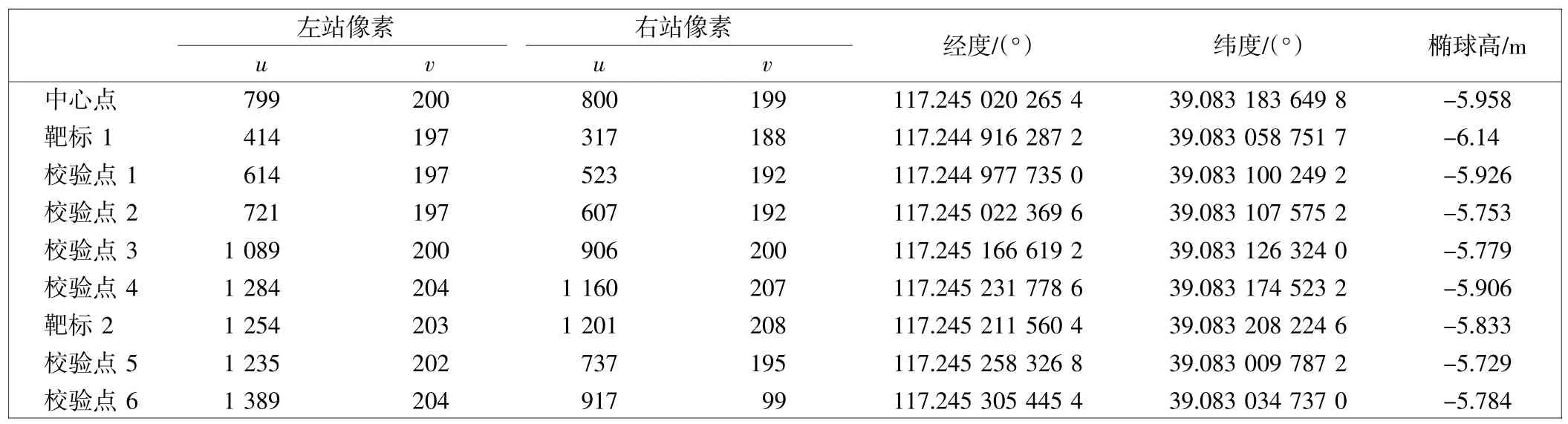
表1 实验数据Tab.1 Experimental data
2.3标定结果
利用表1中的数据和摄像机内外的参数,可计算出参数标定结果如表2和表3所示。

表2 左站参数标定结果Tab.2 Results of left station parameters calibration
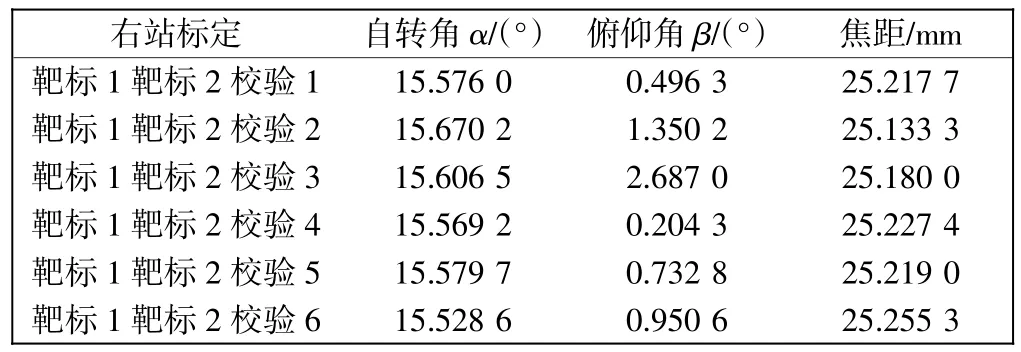
表3 右站参数标定结果Tab.3 Results of right station parameters calibration
为验证该表中参数标定结果的正确性,结合参数的参考值,左右站的自转角分别为αl=15.000°,αr= -15.565°,左右站俯仰角分别为βl=0.3323°,βr=0.524 0°,左右站焦距分别为fl=0.024 785 9 m,fr=0.025 233 8 m。可见,多组标定的结果与参考值均存在微小误差。图6计算了采用以GPS计算为基准的目标坐标,该图显示了各个点的摆放位置。
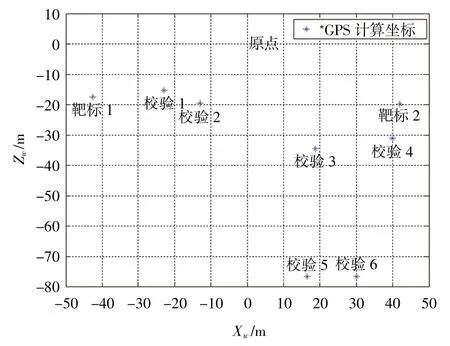
图6 GPS坐标计算Fig.6 Coordinates calculation with GPS
采用参考值和标定值进行坐标的计算,并将其结果分别与采用GPS计算的世界坐标进行比较计算误差,进一步验证标定结果的可靠性。
利用参考值计算坐标和用GPS计算坐标的结果及误差如表4所示。
由于在实验大场景内随机摆放一些目标,所以标定的结果不止一组数据。下面选用一组标定值(靶标1、靶标2和校验点5标定结果)和GPS计算世界坐标结果及误差,如表5所示。
从表4和表5可以看出,以GPS计算的坐标为基准,相对于基准GPS计算的坐标而言,采用标定值计算的坐标与采用参考值计算的坐标误差都在合理范围内。

表4 参数参考值坐标计算Tab.4 Coordinates calculation with referencial parameter values
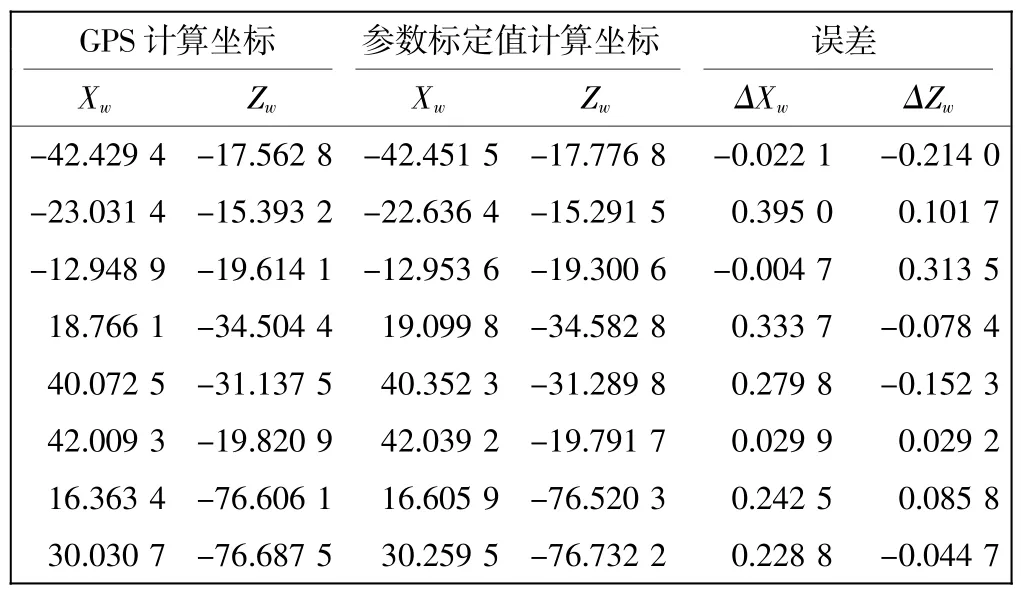
表5 参数标定值坐标计算Tab.5 Coordinates calculation with parameter calibrated values
如图7所示,分别比较表4和表5中ΔXw和ΔZw,可看出二者误差相对较小。在结合参考值的基础上,可运用本文提到的标定方法求取参数,并可将求取的参数用于坐标的求取。
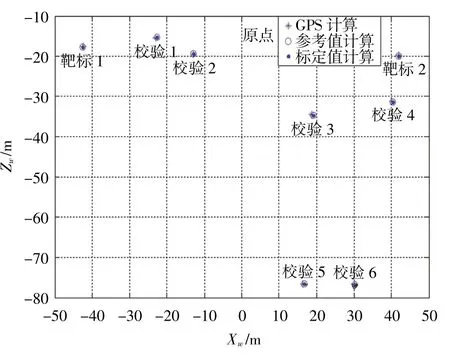
图7 3种方法计算坐标Fig.7 Coordinates calculation with three methods
3 结语
本文实验提出了一种可用于大场景的双目摄像机标定方法。首先分析了参数与坐标的关系,可得出参数的标定结果准确与否对坐标的计算影响显著。由于目标点摆放在多个位置,所以标定结果中不同参数的误差不一致,比较参考值,可看出标定结果的合理性。通过利用标定值求取坐标及误差的对比可看出标定值求取坐标的合理性,实验结果验证了数学模型的正确性,可作为大场景条件下的一种标定方法。
[1]郭昊.几种机场场面监视技术的比较[J].信息科技,2007(15):100,106.
[2]孙红,孙明.机器视觉的标定方法[C]//中国农业工程学会2005年学术年会论文集.广州:中国农业工程学会,2005:358-362.
[3]周薇.基于机器视觉的摄像机标定方法研究[J].电子元器件应用,2008,10(11):70-72.
[4]杨博文,张丽艳,叶南,等.面向大视场视觉测量的摄像机标定技术[J].光学学报,2012,32(9):0915001-1-0915001-9.
[5]寻言言,薛河儒,姜新华.基于MATLAB的相机标定方法[J].内蒙古农业大学学报,2014,35(2):164-168.
[6]陈爱华,高诚辉,何炳蔚.计算机视觉中的摄像机标定方法[J].中国工程机械学报,2006,4(4):498-504.
[7]于泓.摄像机标定算法研究[D].济南:山东大学,2006.
[8]WANG JIAN,WANG XIANG JUN,LIU FENG,et al.A Scheme for Parameter Calibration in Super-Size Two-Dimensional Scale Events Sensing and Positioning System Using Binocular Stereo Vision[C]//The International Society for Optical Engineering,vol 8908,2013.
[9]WANG HUANHUAN,WANG JIAN,LIU FENG,et al.A Verification and Errors Analysis of the Model for Object Positioning Based on Binocular Stereo Vision for Airport Surface Surveillance[C]//Proceedings of SPIE-The International Society for Optical Engineering,vol 9297,2014.
(责任编辑:杨媛媛)
Camera parameters calibration method based on binocular vision system in wide field
WANG Jian1a,WANG Yusheng1a,LIU Feng2,LI Qingjia1b
(1a.College of Electronic Information Engineering;1b.Sino-European Institute of Aviation Engineering,CAUC,Tianjin 300300,China;2.School of Precision Instrument and Optoelectronics Engineering,Tianjin University,Tianjin 300072,China)
A mathematical relationship among world coordinate system,camera coordinate system and image coordinate system is established based on pinhole model of cameras.Explicit expressions of relevant camera parameters are given theoretically,and on this basis,the relationship between parameters and coordinates are investigated. Accuracy of the results for each parameter calibration are verified by obtaining experimental data.According to the relationship between target coordinates(u,v)in the image coordinate system and its corresponding coordinates in the world coordinate system,all coordinates are calculated based on the results of above calibration.Then these coordinates are compared with the coordinates calculated by GPS and parameter reference values respectively.Finally,a method of camera calibration is proposed based on binocular vision within an error permissible range.
binocular vision system;pinhole model;camera calibration;object positioning;world coordinate system;
V355;TP391
A
1674-5590(2016)03-0001-05
2015-07-01;
2015-09-26基金项目:国家自然科学基金项目(61179043)
王剑(1961—),男,江苏徐州人,教授,工学博士,研究方向为通信与信息系统.

