动态轴向载荷下谐振梁振动响应分析*

邢维巍，张硕，樊尚春

（北京航空航天大学仪器科学与光电工程学院，北京100191）

动态轴向载荷下谐振梁振动响应分析*

邢维巍*，张硕，樊尚春

（北京航空航天大学仪器科学与光电工程学院，北京100191）

在航空航天飞行控制中，为实现关键参数的高精度高动态测量，急需发展具有快速响应特性的谐振式传感器。谐振式传感器本质上是输入与谐振器振动状态之间的映射。这种映射一般通过跟随输入的轴向载荷调制谐振梁的固有频率实现。高动态应用中的核心问题是动态轴向载荷下谐振梁的振动响应。利用基本的微元力学平衡关系建立了动态轴向力作用下谐振梁振动行为的数学模型。此模型比Mathieu方程的适用面更广，在一般假设下更难以进行解析或数值求解。为此引入了等效电路方法进行模型求解。通过对等效电路的仿真，得到了谐振梁在多种典型动态载荷下的振动响应。动态轴向载荷对于谐振梁的作用具有强烈的非线性和独特的规律，值得进一步深入研究探讨。

谐振传感器；动态载荷；等效电路；振动响应；Mathieu方程

EEACC：0220；1200；7310Gdoi：10.3969/j.issn.1004-1699.2016.09.013

硅微机械谐振式压力传感器具有高精度、高分辨率、高稳定性的优点［1］，是航空航天高精度压力测量的主要手段之一。随着飞行器技术要求的提高，高精度压力传感器应用场合从普通的飞行状态监测逐渐扩展到飞行控制，成为闭环控制系统的一环。应用的升级对传感器的性能，尤其是动态性能提出了苛刻的要求。

谐振式传感器利用谐振器的固有振动特性进行测量，本质上是输入与谐振器振动状态之间的映射［2］。硅微机械谐振式压力传感器中，这种映射通过跟随输入的轴向载荷调制谐振梁的固有频率实现。高动态应用中的核心问题是动态轴向载荷下谐振梁的振动响应。

关于动态载荷下梁的振动，一类研究主要关注移动力作用下梁的响应问题［3-7］，另一类主要研究微机械谐振式陀螺中的谐振梁，属于动态轴向载荷问题。其中的最新研究将振梁的动力学特性归一到Mathieu方程，利用小参数摄动法得到具有调频特性的稳定近似解，并应用到陀螺的信号解调［8］。这种方法只能解决正弦周期载荷问题。本文试图从理论上探讨动态载荷对欧拉梁振动特性的作用机理，建立更一般形式的动态轴向载荷下梁的振动模型，并给出求解该模型的便捷实用的技术方法。

1　动态轴向载荷下梁的振动模型

假设谐振梁在动态轴向载荷的作用下，各截面的中心惯性轴在同一平面内，谐振梁在该平面内做横向振动，这时梁的主要变形是弯曲变形，可以忽略剪切变形和截面绕中心轴转动惯量的影响，称为伯努利-欧拉梁。受力模型如图1所示。以微段dx为研究对象，受力分析如图2所示。

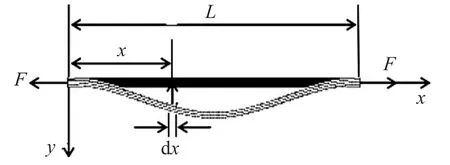
图1　动态轴向载荷作用下双端固支梁弯曲振动示意图

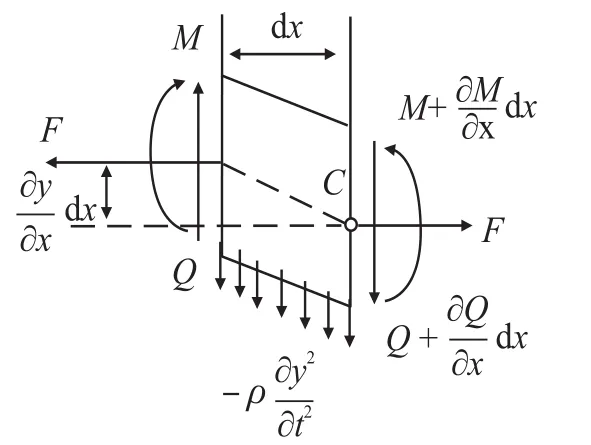
图2　谐振梁微段dx受力分析

图中各项的物理意义：F为梁承受的轴向载荷；ρ为梁的密度；E为梁的弹性模量；I为梁横截面对中性轴的惯性矩；A、L、h、b分别为梁的横截面积、长度、高度、宽度。设y（x，t）是梁上距原点为x处的截面在t时刻的横向位移，由力矩平衡公式与弯矩平衡公式共同联立得梁横向弯曲振动的方程为：

用分离变量法求该方程的解，设方程的解为：

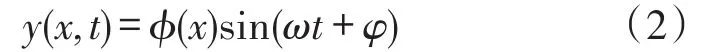
其中ω为梁振动的固有频率，Y（x）为梁振动的模态函数。则式可变形为：

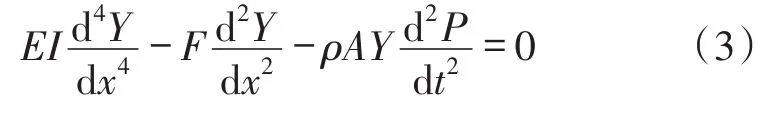
分析谐振梁在不受外力自由振动情况，将双端固支梁的边界条件（固定端梁的挠度和转角均等于零）代入，解得梁自由振动振型公式：

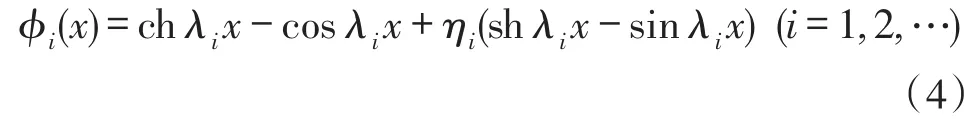
根据文献［9］，可知谐振梁振动的第1阶振型固有频率解为：

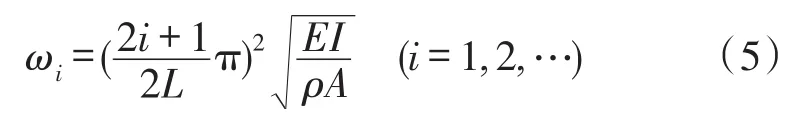
谐振梁以一阶振型为工作模态，根据文献［9］，表6.3查得λL=4.730，对应参数：

得出梁自由振动一阶振型公式：

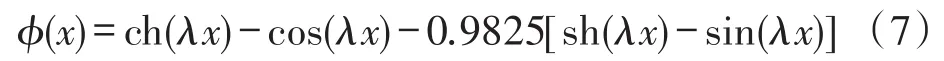
式两边都乘以Y（x），再对x进行积分，由分部积分法以及齐次边界条件可得：

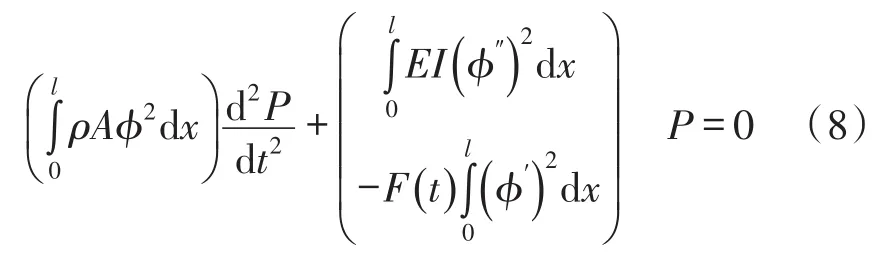
式简化可写为：

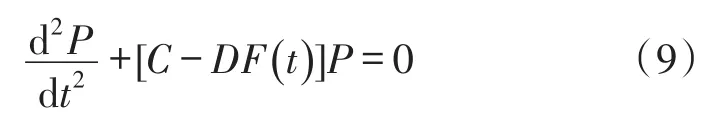
其中C，D为常量。这就是一般载荷形式作用下梁的振动模型。

输入载荷为正弦时，通过如式的变量代换：

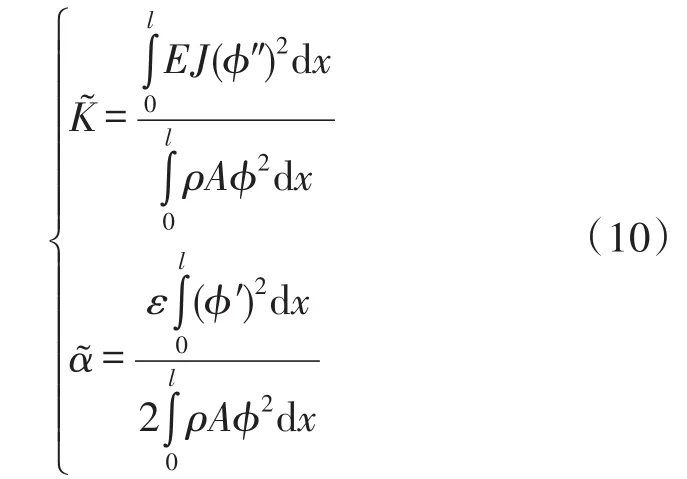
式可转换为式：

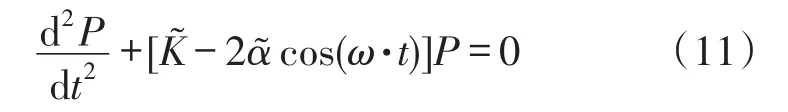
此即标准形式的Mathieu方程［10］。

由公式可得Mathieu方程虽然可以推导出在动态输入载荷下谐振梁的振动模型，但是Mathieu方程要求输入载荷F为正弦信号［10］，因此有局限性。由于该法公式模型的局限性，动态输入载荷F只可以为三角函数的形式，且动态输入载荷F不满足叠加性。故本论文用建立等效电路的方法［11-12］模拟动态轴向载荷下谐振梁振动方程特性，来实现动态输入载荷的普遍性。

2　动态轴向载荷下谐振梁振动模型电路模拟

根据已经建立的动态轴向载荷下谐振梁振动模型建立输出谐振梁振动信号的等效电路，如图3所示。

其中电压源V2即对应系统中的动态轴向载荷，通过改变电压源的输出来模拟动态力的加载模式（在本文中用载荷来表示电压源）。

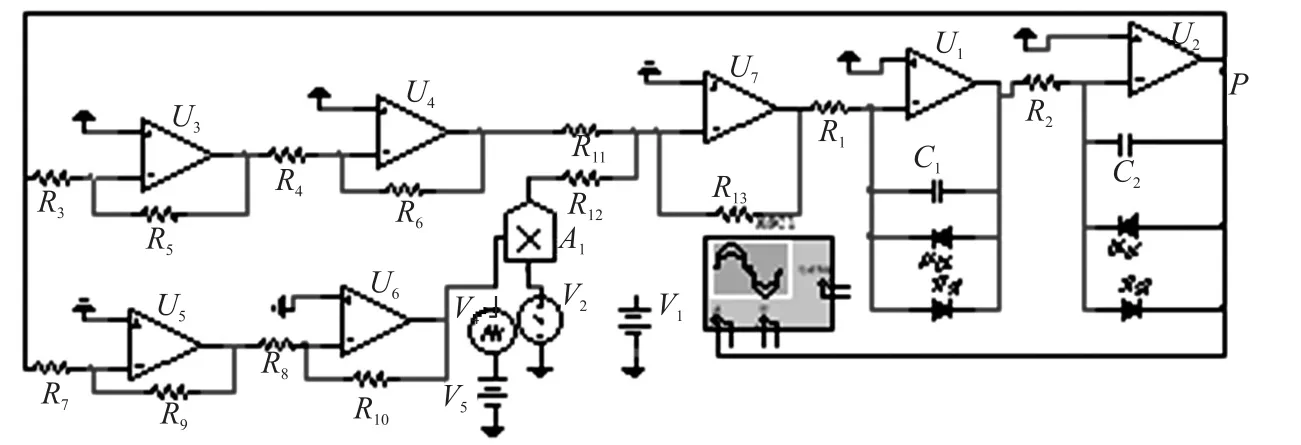
图3　输出谐振梁振动响应的等效电路

取R11=R12=R13，则其输出方程为：

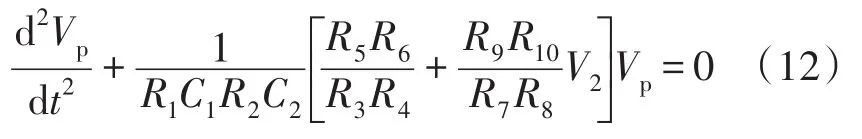
通过调节电阻电容的值，使式与式相对应。对应关系：

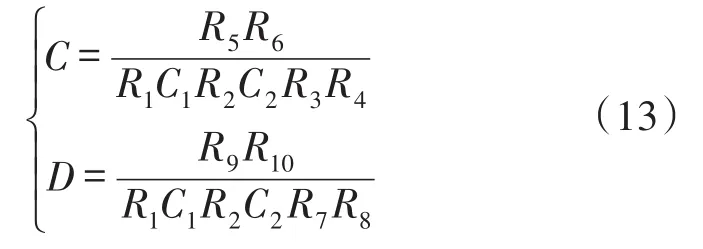
3　动态轴向载荷下谐振梁振动模型等效电路输出结果分析

首先分析固有频率部分，当电压源无输出时，电路自激振荡周期为15 μs，与谐振梁固有频率相符合。输出波形如图（如下无特殊说明，幅值比较小的曲线为电压激励，仿真图横轴标度50 μs/div）。

图4　未加载荷时输出波形

直流电压载荷下，改变载荷的强度对比输出波形。波形如图5（纵轴输出与输入标度比为25∶1）。

图5　直流载荷下的输出波形

由图5输出的波形图，当载荷数值变大时，输出的波形幅值变小，频率变小。对应在谐振系统中，改变轴向载荷的大小能影响谐振梁振动的幅值与频率。轴向载荷越大，谐振梁振幅越小，频率越小。

转换电压载荷模型为具有一定频率交流模型来分析。保持电压值不变，改变电压载荷频率。继续进行仿真（纵轴输出与输入标度比为100∶1）。

从图6仿真结果可以看出，当保持载荷不变，通过调节载荷频率会对输出波形的幅值及频率都有影响，当载荷频率变大时，输出频率以及幅值随之变大。当载荷频率超过一定值时，输出频率及幅值不再随之，变大。因此得出动态轴向载荷大小不变，而频率在变动时，对谐振梁振动频率及幅值都有影响。

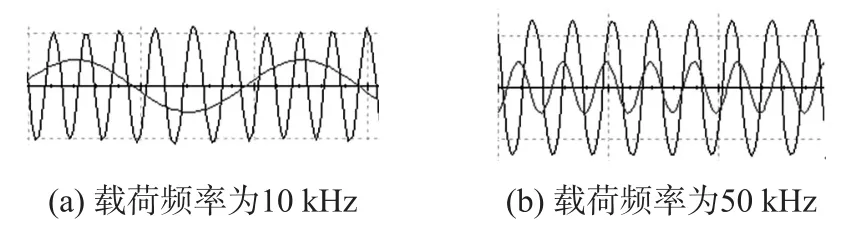
图6　保持载荷幅值10 mV不变改变频率时输出波形

保持载荷频率不变，改变电压载荷幅值。继续进行仿真。

继续增加电压载荷幅值出现输出波形被调制的现象（图8纵轴与图7纵轴坐标比为2∶1）。

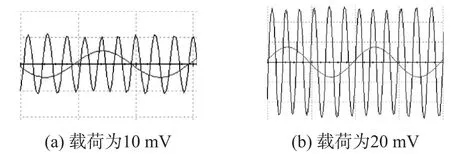
图7　载荷频率10kHz幅值不同时输出波形

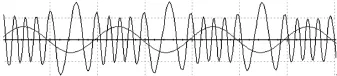
图8　电压载荷为50 mV 10 kHz时的输出波形

从图7、图8可以明显看出，当频率不变而载荷的幅值变大时，输出响应的幅值随之变大，输出响应的频率也随之改变，从图9可以看出此规律同样适用于特殊波形如三角波。而当载荷幅值超过一定数值时（如图8），输出响应的频率被调制的现象比较明显，此时参数的取值在Mathieu方程的稳定范围内，振荡过程同时存在着振幅调制与频率调制。当外载荷达到极大值点时振动系统刚度最大，振荡频率最高，但伴随着有幅度下降的现象出现振幅下降的现象。与文献［8］结论一致。

图9　载荷为60 mV 10 kHz三角波时的输出波形

对比轴向载荷下谐振梁振动的机械系统，当外载荷达到极小值点时振动系统刚度最小，由于刚度的松弛，谐振频率下降的同时可以看出振荡幅度显著上升。这种幅度调制现象随着频率调制力度的增强而增强，属于参数载荷系统固有的现象。

4　结语

本文根据力学平衡建立了动态轴向载荷下谐振梁振动的数学模型，利用等效电路方法获得了该模型在一系列典型载荷下的响应。谐振梁在动态载荷下的响应对于载荷的幅度、频率、相位、占空比都极其敏感，并表现出强烈的非线性特征。可见，谐振梁在动态载荷下的行为是相当丰富的，值得继续深入研究。

［1］樊尚春.传感器技术及应用［M］.北京航空航天大学出版社，2004.

［2］樊尚春，刘广玉.热激励谐振式硅微结构压力传感器［J］.科学技术与工程，2004，21（5）：426-429.

［3］Piccardo G.Dynamic Response of Euler-Bernoulli Beams to Reso⁃nant Harmonic Moving Loads［J］.Structural Engineering&Me⁃chanics，2012，44（5）：681-704.

［4］Piccardo G，Ranzi G.A Complete Dynamic Approach to the Gen⁃eralized Beam Theory Cross-Section Analysis Including Extension and Shear Modes［J］.Mathematics&Mechanics of Solids，2013，19（8）：900-924.

［5］Silvestre N，Camotim D.Shear Deformable Generalized Beam The⁃ory for the Analysis of Thin-Walled Composite Members［J］.Jour⁃nal of Engineering Mechanics，2013，139（8）：1010-1024.

［6］杨甲山.时间模上一类二阶非线性动态方程的振动结果［J］.安徽大学学报（自然科学版），2015，39（1）：1-7.

［7］Greenwood J C，Satchell D W.Miniature Silicon Resonant Pres⁃sure Sensor［J］.Control Theory&Applications Iee Proceedings D，1988，135（5）：369-372.

［8］Fan Shangchun，Li Yan，Guo Zhanshe，et al.Dynamic Character⁃istics of Resonant Gyroscopes Study Based on the Mathieu Equa⁃tion Approximate Solution［J］.Chinese Physics B，2012，21（5）：58-65.

［9］倪振华.振动力学［M］.西安：西安交通大学出版社，1989.

［10］N W.McLACHLAN：Theory and Application of Mathieu Func⁃tions［M］.Dover Publicatons，Inc.USA.1964.

［11］张燕琴，邢维巍，景标.基于V-F变换的硅压阻压力传感器的处理电路［J］.传感技术学报，2016，29（2）：161-165.

［12］王光庆，刘创，张伟，等.悬臂梁式压电双晶片振动能量采集器的模型与实验研究［J］.传感技术学报，2015，28（6）：819-824.

邢维巍（1973-），男，副教授，现于北京航空航天大学仪器科学与光电工程学院任教，主从事谐振式传感器的动态特性及信号处理的研究，xingweiwei@buaa.edu.cn；

张硕（1993-），女，北京航空航天大学仪器仪表工程专业硕士研究生，主要研究方向为谐振式传感器的动态特性及信号处理，xiaoshuo@bupt.edu.cn。

Resonant Beam Vibrating Response under Dynamic Axial Load Analysis*

XING Wewei*，ZHANG Shuo，FAN Shangchun
（School of Instrument Science&Opto-electronics Engineering，Beihang University，Beijing 100191，China）

In the field of aero and space flight control，in order to realize high accuracy and high dynamic measure⁃ment of key parameters，it is urgent to develop resonant transducers with fast response feature.A resonant sensor is essentially a mathematical mapping between the input and the vibration state of the resonator.This mapping is usu⁃ally implemented by modulating the natural frequency of the resonant beam by an axial load following the input.The core issue in high dynamic applications is the vibration response of the resonant beam under dynamic axial load.The mathematical model of resonant beam vibrating behavior under dynamic axial load was established through the basic micro element mechanical balance relationship.This model can be applied in more fields than the Mathieu equation，and it is more difficult to be solved analytically or numerically.Thus the equivalent circuit meth⁃od was introduced to solve the model.By simulation on the equivalent circuit，vibration response of resonant beam under several typical dynamic loads was obtained.Dynamic axial load has a strong nonlinear effect on the resonant beam with unique rules，indicating that this problem is valuable for further research and discuss.

resonant sensor；dynamic load；equivalent circuit；vibration response；Mathieu equations

TP212.1

A

1004-1699（2016）09-1372-04

项目来源：国家重大科学仪器设备开发专项项目（2014YQ350461）；国家自然基金项目（61273060，60804062）；长江学者和创新团队发展计划项目（IRT1203）

2016-03-08修改日期：2016-04-13