盾构施工临近建筑物变形影响因素关联性分析

张立茂，冉连月，吴贤国，覃亚伟

(华中科技大学土木工程与力学学院，武汉　430074)



盾构施工临近建筑物变形影响因素关联性分析

张立茂，冉连月，吴贤国，覃亚伟

(华中科技大学土木工程与力学学院，武汉430074)

基于大量工程实践和资料对建筑物变形安全影响因素进行分析，基于实际数据样本利用粒子群和支持向量机算法，得到影响因素与建筑物变形特征之间的关联模型，并对模型进行验证，利用蒙特卡洛模拟算法仿真模拟得到大量仿真样本，利用卡方关联分析方法和灰色关联算法对各影响因素的关联度进行挖掘，了解各个影响因素与建筑物变形特征之间的关联性程度，进一步得出需要重点控制的建筑物变形的关联影响因素，为临近建筑物的保护控制提供决策参考。

地铁；盾构隧道；施工；建筑物变形；影响因素；关联性分析

城市地铁盾构施工大多位于城市中心地带，将对地面交通和地表建筑物造成重要影响，尤其是对于临近建筑物，如果不能及时发现和控制建筑物变形安全，将对人民群众生命财产造成严重损失。盾构施工对建筑物的破坏主要是变形破坏，变形破坏程度直接决定建筑物的安全状况。盾构施工诱发临近建筑物变形安全受到施工参数、地质条件、建筑物自身特点等多个方面因素的影响，各种影响因素之间既独立作用，又相互约束。因此，有效分析盾构施工对建筑物变形的影响，分析建筑物变形影响因素的关联性，加强重要关联因素的控制，将使得建筑物安全控制达到事半功倍的效果。

国内外学者针对盾构施工中相关地质参数及施工参数与建筑物变形之间的关联关系展开了一系列研究，主要分析研究方法可以归结为以下几类：经验公式法、理论解析法[1]、智能预测分析方法[2]。经验公式法中Peck[3]公式最为经典，“Peck公式”能够快速得到地表的初步变形，由于没有考虑建筑物自身情况等的影响，不能够准确反映建筑物变形的关系[4]，因此不能简单地利用地表变形经验公式来模拟预测建筑物变形情况；理论解析法主要是依据土体力学模型以及建筑物结构力学模型等理论[5]建立建筑物变形机理模型，然后对现场监测数值进行模拟分析[6]。姚爱军等人[7]采用FLAC3D工程分析模型，结合现场监测对盾构施工建筑物变形进行模拟分析，分析得到盾构施工中建筑物变形的关键因素。

随着计算机科学技术的发展，以人工智能、灰色理论等为代表的软科学理论与工程实践结合，催生了一批智能预测方法模型。谭鹏和曹平[8]针对盾构施工中沉降与影响因素之间的关联关系利用支持向量机模型构建出两者的非线性映射关系。如果预测结果能够验证说明智能方法预测的准确性，那么也说明智能算法的黑箱模型能够很好地描述因素与变形特征之间的关联关系。目前的研究未能进一步对黑箱关联模型进行深度挖掘，因此，本文将针对智能算法得到的黑箱关联模型，利用专业的关联分析方法对关联因素的关联度展开深入分析，构建基于最小二乘支持向量机智能算法的建筑物变形关联关系模型，利用模型描述建筑物变形影响因素与变形特征之间的关联关系；然后在蒙特卡洛模拟仿真的基础上利用卡方关联分析方法和灰色关联分析方法分析影响因素与建筑物变形特征之间的关联度。

1　临近建筑物变形影响因素分析

地层变形是盾构施工影响与临近建筑物变形之间传递的主要过程，无论是水平地层变形还是竖向地层变形，都将对临近建筑物基础变形造成严重影响。盾构施工引起地层变形，地层变形大小与盾构施工中隧道相关参数、施工参数相关以及岩土层物理性能参数指标相关。当地层变形传递至建筑物时，建筑物发生变形，如果建筑物自身状态比较好，建筑物抵抗变形的能力就强，变形就小，因此建筑物变形破坏程度也与建筑物自身状态有一定关系。

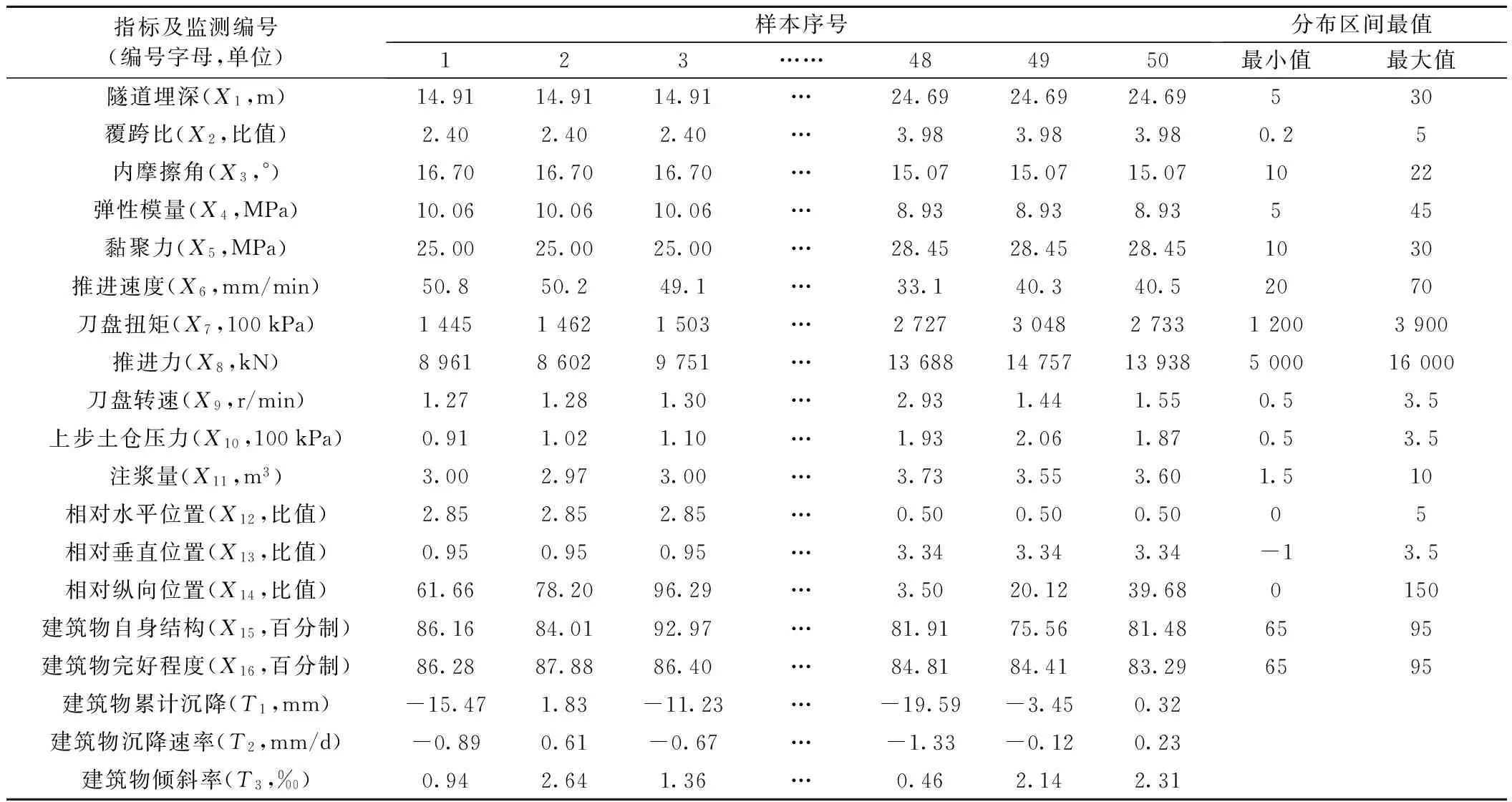
基于大量工程实际经验和查阅大量文献，将建筑物变形影响因素分为隧道相关因素、岩土层物理性能因素[9]、盾构施工因素[10]、建筑物因素4类。其中隧道相关因素中隧道埋深、覆跨比以及隧道直径等因素对周围环境影响最为明显，岩土层物理性能参数指标中内摩擦角、泊松比、黏聚力、弹性模量等参数指标对地层变形有着重要影响[11]，盾构施工因素[12]中本文选取刀盘扭矩、推进速度、推进力、上部土仓压力、刀盘转速、注浆量等重要因素进行分析研究，建筑物因素中一方面和建筑物与隧道相对位置有关，同时也和建筑物自身条件相关。基于此，建立盾构施工引起临近建筑物变形影响因素指标体系如表1所示。

2　建筑物变形实测值与数值模拟分析

在分析盾构施工引起建筑物变形影响因素的基础上，为进一步分析各影响因素的关联性，将对建筑物变形进行实测值与数值模拟分析。首先，利用最小二乘支持向量机构建盾构施工引起建筑物变形分析模型，并验证模型的准确性；然后，利用蒙特卡洛模拟算法仿真模拟得到仿真样本；最后，在模拟仿真的基础上，利用统计方法和曲线拟合方法分别对影响因素进行关联分析。

表1　盾构施工引起临近建筑物变形影响因素指标体系

2.1建筑物变形最小二乘支持向量机关联模型建立

支持向量机(SVM)能够很好地实现对小样本复杂非线性数据的预测分析，有着强大的预测能力，其中最小二乘支持向量机(LSSVM)由常规的支持向量机拓展而来，能够大大提高求解问题的速度和收敛精度[13]，张慧源和顾宏杰等研究利用最小二乘支持向量机完成对载流故障趋势预测分析，并证明其在进行小样本预测中的优势[14]。在进行建筑物变形数值仿真前需建立一个建筑物变形影响因素关联分析模型，在模型被验证有效的前提下才可以进行数值仿真[15]。因此，将选用最小二乘支持向量机来构建监测数据预测分析模型[16]。基于最小二乘支持向量机建筑物变形影响因素关联分析模型构建思路如图1所示。

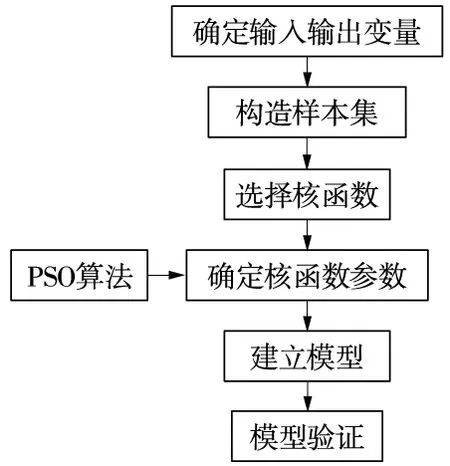
图1　建筑物变形最小二乘支持向量机模型建立

2.2建筑物变形蒙特卡洛数值仿真

蒙特卡洛方法(Monte Carlo method)，是一种以概率统计理论为基础的统计模拟方法。其实质是根据研究对象服从的分布对现实中研究对象可能出现的情况进行模拟。通过对现实情况的大量模拟试验，可以得到更加符合实际的有价值的统计结论。理论上模拟次数越多，其结果越符合实际情况，随着计算机技术的不断发展，模特卡洛方法得到了广泛的应用，故本文采用蒙特洛卡数值仿真。

建筑物变形蒙特洛卡数值仿真就是依据蒙特卡洛模拟思想[17]，在确定建筑物变形支持向量机模型输入变量分布情况的基础上，对模型进行模拟得到建筑物变形特征值，然后利用其他方法分析各输入因素变量与变形特征变量之间的关系。建筑物变形蒙特卡洛仿真模拟的步骤如下。

(1)根据经验和历史数据，利用根据样本数据结合专家群决策方法构造建筑物变形各影响因素指标的概率正态模型。

(2)利用随机数发生器抽样取出因素指标随机值，并代入经过验证的建筑物关联模型得到建筑物变形特征的大量仿真值。

(3)重复步骤(2)，模拟多次得到一系列建筑物变形特征的仿真值。

2.3建筑物变形影响因素关联分析

基于统计学理论的关联分析方法和灰色关联分析方法是目前最为常用的多因素关联分析方法。为能准确分析因素指标的关联性，采取综合关联分析方法，该方法分别利用卡方检验和灰色算法计算得到卡方关联度以及灰色关联度，然后再利用方根法确定最终关联系数。具体内容如下。

(10)

2.3.1统计学关联分析

χ2检验核心是构建Pearsonχ2统计量如下

(1)

式中，E为期望频数；O为观察频数差别之和；χ2值近似服从χ2分布，其自由度为ν。设2个不同的特征变量A与B，基于χ2检验的A与B关联性分析的基本步骤如下。

(1)构建样本数理论值

假设A和B取值均为离散(样本总数为N)：

{a1，a2，…，am-1，am}：A的取值范围；

{b1，b2，…，bm-1，bm}：B的取值范围；

tij：(ai，bi) 的样本数；

pi：ai的样本在A特征变量中的个数

(2)

qj：bj的样本在B特征变量中的个数

(3)

(2)假设检验

(4)

(5)

(3)计算卡方关联度

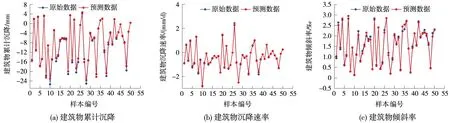
当两者相关时，利用式(6)计算两者的相关程度r1(0

(6)

2.3.2灰色关联分析

基本分析步骤如下。

(1)确定分析数列

确定一个因变量和多个自变量因素，因变量所组成的序列成为参考序列{X0}，自变量所组成的序列成为比较序列{Xi}。

(2)无量纲化处理

无量纲化处理的思路是以变量实际值和参考值之间的比值代替实际值。初值化法以第一个变量值为参考值，可以很好地表现变量序列后续变量值的动态变化趋势，因此本文采用初值化方法。

(3)求最大最小差、差序列

首先利用式(7)计算序列的差序列Δi(k)，然后在差序列的基础上再利用式(8)和式(9)计算最大差a和最小差b

(7)

(8)

(9)

(4)计算灰色关联系数

式中，θ为分辨系数，取值范围(0，1)，一般取θ=0.5。

(5)计算灰色关联度r2(0

(11)

2.3.3综合关联分析

在得到卡方关联分析r1和灰色关联分析r2的结果后，根据方根法利用公式(12)计算得到综合关联度r(0

(12)

3　实证分析

3.1工程概况

武汉地铁7号线是继2号线、4号线后第3条穿越长江的地铁线，一期起于东方马城，经王家墩，沿建设大道、澳门路，从三阳路过长江，然后折向武昌火车站，沿恒安路、李纸路至终点野芷湖，设停车场、车辆段各1处。7号线一期线路全长30.85 km，全为地下线，共设车站19座。

盾构施工于2014年8月24日10时16分从东方马城站—长丰站右线区(东长区间)的东方马城站成功始发，为保证盾构施工过程中建筑物安全，武汉市地铁集团邀请第三方对建筑物累计沉降(T1)、建筑物沉降速率(T2)、建筑物倾斜率(T3)等方面进行监测。从武汉地铁7号线途径附近的建筑群中选取10栋建筑物，并针对每栋建筑物取5个监测时间点构建50个支持向量机模型样本，以及根据模型样本数据结合专家经验构造基于最小二乘支持向量机智能算法的建筑物变形各影响因素指标的均匀分布区间。如表2所示。

表2　建筑物变形支持向量机模型样本以及指标分布区间

图2　PSO-LSSVM建筑物关联模型辨识结果

3.2建筑物变形数值模拟仿真

首先利用PSO-LSSVM(基于最小二乘支持向量机的粒子群优化算法)预测模型公式得到建筑物变形关联模型，模型辨识结果如图2所示。为验证支持向量机模型的有效性和准确性，利用预测检验方法进行检验，检验结果如表3所示。由表3可知，建筑物关联模型单根性检验和正态性检验均满足要求，其有效度均达到0.95，由此证明基于PSO-LSSVM的建筑物关联模型是准确有效的。

表3　建筑物变形关联模型检验结果

3.3建筑物影响因素关系性分析

利用公式(6)对表4中模拟仿真数据进行卡方分布关联性分析，分析结果r1如表4所示。

表4　综合关联系数计算结果

由表4可知，16个因素与3个变形特征存在一定的关联关系，不同的相关系数，表明在样本范围内因素对变形特征的影响程度不同；然后，利用式(11)计算得到灰色关联分析结果r2如表4所示；最后利用式(12)计算综合关联系数r如表4所示，各影响因素关联性对比分析如图3所示。由表4及图3可知，基于武汉地铁7号线样本数据分析，其中对于建筑物累计沉降特征，影响因素X9、X11、X16(X9：刀盘转速，X11：注浆量，X16：建筑物完好程度)为强关联重要影响因素，且关联度大于0.5；对于建筑物沉降速率变形特征，影响因素X9、X11为关联度大于0.5的强关联重要影响因素；对于建筑物倾斜变形特征，影响因素X9、X11为关联度大于0.5的强关联重要影响因素。在施工过程中应该加强对重要影响因素的关注，提前针对重要影响因素制定相应的策略，以确保施工过程中建筑物变形安全。

图3　各因素与建筑物变形特征的关联性对比分析

4　结论

(1)本文将建筑物变形影响因素分为隧道相关因素、岩土层物理性能因素、盾构施工因素、建筑物因素4类，具体细分为16个指标，形成一个建立盾构施工引起临近建筑物变形的影响因素指标体系。

(2)本文构建基于最小二乘支持向量机智能算法的建筑物变形关联关系模型，利用支持向量机黑箱模型描述建筑物变形影响因素与变形特征之间的关联关系，然后在蒙特卡洛模拟仿真得到大量仿真样本的基础上，利用卡方关联分析方法和灰色关联分析方法分析影响因素与建筑物变形特征之间的关联度。

(3)实证分析中将建筑物变形空间影响因素分析方法应用于武汉市地铁7号线东长区间建筑物变形安全控制中，通过分析可知：其中关联度大于0.5的重要影响因素包括盾构施工因素中的刀盘转速X9和注浆量X11，以及建筑物因素中的建筑物完好程度X16，在施工管理过程中通过加强对这些重要因素的关注，能够有效提高建筑物安全管理事中控制的效率。

[1]Miliziano S, Soccodato F M, Burghignoli A. Evaluation of damage in masonry buildings due to tunnelling in clayey soils[Z]. 2002：335-340.

[2]Suwansawat S, Einstein H H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunnelling[J]. Tunnelling and Underground Space Technology, 2006,21(2):133-150.

[3]Peck R B, Peck R B. Deep excavations and tunnelling in soft ground[C]∥Proc. 7th Int. Conf. on SMFE. 1969.

[4]韩煊.隧道施工引起地层位移及建筑物变形预测的实用方法研究[D]. 西安：西安理工大学,2007.

[5]Mroueh H, Shahrour I. Three-dimensional finite element analysis of the interaction between tunneling and pile foundations[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002,26(3):217-230.

[6]姚爱军，向瑞德，侯世伟.地铁盾构施工引起邻近建筑物变形实测与数值模拟分析[J].北京工业大学学报，2009(7):910-914.

[7]于丹丹，双晴.地铁隧道施工邻近建筑物安全风险评价[J].城市轨道交通研究，2013,16(4):32-37,102.

[8]谭鹏，曹平.基于灰色关联支持向量机的地表沉降预测[J].中南大学学报：自然科学版，2012(2):632-637.

[9]张成平，骆建军，张顶立，等.地铁施工对邻近建筑物安全风险管理[J].岩土力学，2007,28(7):1477-1482.

[10]周红波，何锡兴，蒋建军，等.地铁盾构法隧道工程建设风险识别与应对[J].地下空间与工程学报，2006(3):475-479.

[11]张志华，周传波，夏志强，等.地铁隧道土体参数敏感性分析与正交反演[J].中南大学学报：自然科学版，2013(6):2488-2493.

[12]陈秋鑫,李俊才,刘光臣,等.盾构施工安全穿越禄口机场复合地层段的数值模拟与监测分析[J].铁道标准设计，2014(12)：94-98.

[13]辛治运，顾明.基于最小二乘支持向量机的复杂金融时间序列预测[J].清华大学学报：自然科学版，2008(7):1147-1149.

[14]张慧源，顾宏杰，许力，等.基于最小二乘支持向量机的载流故障趋势预测[J].电力系统保护与控制，2012(10):19-23.

[15]ZHANG Limao, WU Xianguo, Miroslaw J. Skibniewski. Dynamic risk analysis for adjacent buildings in tunneling environments: A Bayesian network based approach[J]. Stochastic Environmental Research and Risk Assessment, 2015(29):1447-1461.

[16]ZHANG Limao, WU Xianguo, DING Lieyun, Miroslaw J. Skibniewski. A Novel Model for Risk Assessment of Adjacent Buildings in Tunnelling Environments[J]. Building and Environment, 2013(65):185-194.

[17]宋克志，王梦恕.基于数值模拟的盾构隧道地表变形的可靠度分析[J].铁道标准设计，2004(6):71-73.

Correlation Analysis of Influence Factors of Building Deformation near the Shield Construction

ZHANG Li-mao， RAN Lian-yue， WU Xian-guo， QIN Ya-wei

(School of Civil Engineering & Mechanics， Huazhong University of Science & Technology， Wuhan 430074， China)

This article analyzes the influence factors relating to building deformation based on engineering practices and information. The particle swarm algorithm and support vector machine (SVM) are used to obtain the correlation model between influence factors and deformation characteristics and the model is verified. Finally， the related model simulation samples are obtained by means of Monte Carlo Simulation Algorithm Simulation to define the degree of the correlation between each influence factor and building deformation with chi-square correlation analysis method and gray correlation algorithm．

Metro; Shield tunnel; Construction; Building deformation; Influence factor; Correlation analysis

2015-12-21；

2016-01-15

张立茂(1987—)，男，博士研究生，2009年毕业于华中科技大学工程管理专业。

1004-2954(2016)09-0094-05

U456.3+3

ADOI:10.13238/j.issn.1004-2954.021