采用克里金插值法分析河北地区地磁场变化特征
董 博纪春玲张环曦李 凤周安聘牛淑瑜赵雨晨刘 静刘 檀朱音杰
1)中国石家庄050021河北省地震局
2)中国石家庄050021河北地质大学
采用克里金插值法分析河北地区地磁场变化特征
董 博1),2)纪春玲1)张环曦1)李 凤1)周安聘1)牛淑瑜1)赵雨晨1)刘 静1)刘 檀1)朱音杰1)
1)中国石家庄050021河北省地震局
2)中国石家庄050021河北地质大学
通过克里金插值方法,对河北地区2011—2014年地磁场中总强度F值及垂直分量Z值数据进行计算,分析该区近期地磁场变化特征。结果表明:在地震活动较为平静状态下,河北地区地磁场变化与地理纬度改变具有密切关系,与地理经度变化关系不大;F值与Z值等值线分布与地磁台站分布有关,且随时间增加而增大。
地磁场;克里金插值法;等值线
0 引言
众所周知,地球磁场随时间缓慢变化,对这种地球基本磁场长期变化的研究,是地球物理学的重要课题之一。地磁场由不同磁场叠加,按其性质,可分为来源于地球内部并构成地磁场主要成分的稳定磁场和起源于地球外部的变化磁场。同时,地磁场有各类长期与短期变化,只有研究并充分认识其规律,才能正确提取异常场。因此,分析、研究某一地区地磁场变化特征,可以进一步认识该区地磁场活动规律,排除非震干扰信息,捕获真正有用的地震前兆信息(张小涛等,2008)。
由于地磁场的分布和变化具有空间上的相关性和时间上的延拓性,可以根据时空分布特征,采用物理意义明确的数学方式来描述(薛革等,1995)。本文主要利用精度较高的克里金插值方法,对2011—2014年河北及周边地区质量较好且连续率较高的11个定点地磁台站观测资料进行分析。河北省及周边地区地磁台站分布较合理,地磁观测数据可以反映该区域地磁场时空变化。通过对河北地区地磁场进行时空分布特征的分析计算,得到该地区近期地磁场时空分布演变规律及特征,不仅对了解地磁场变化形态具有意义,且有助于识别地磁异常信号,为提取更有价值的地震地磁异常信息做好准备工作(张小涛等,2008)。
1 资料收集
河北省现有10个地磁观测台站,因黄壁庄台、文安台、顺平台近年才开展数字化观测,观测资料大量缺记,故选用其他7个连续性较好、数据质量可靠的地磁观测资料作为研究对象。为了有效减小边界效应,并考虑地震台站间距及分布,增加河北周边地区4个地震台(辽宁朝阳台、河南浚县台、山西大同台、山东济南台)地磁观测资料参与研究。各台站参数见表1,地震台分布见图1。
大量震例表明,地磁垂直分量Z震前异常比其他分量明显多(解用明,1996),因此本文选取地磁场总强度F及垂直分量Z研究河北地磁场近期变化,并考虑地震活动较为平静时期及最新资料两个因素。统计可知,每年8月地磁暴相对较多,地磁场扰动相对较大,而12月地磁场相对平稳,且2011—2014年每年8月和12月全球地震,尤其大震发生次数相对较少,故选取该时段8月和12月地磁F值、Z值月均值进行分析,见表2、表3。
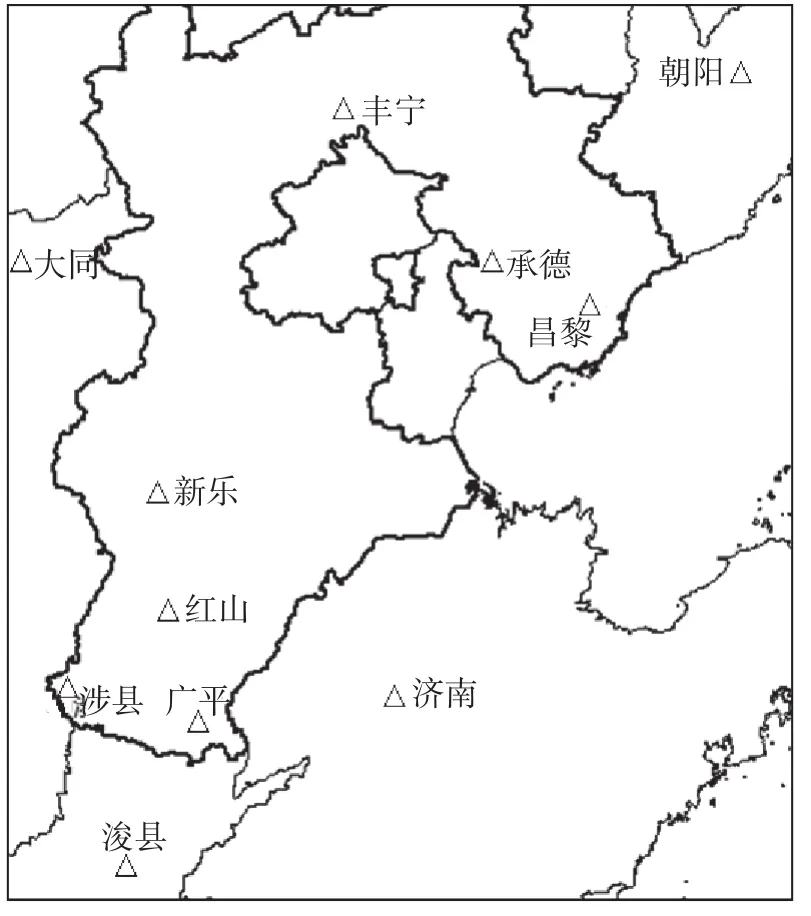
图1 相关地磁台站分布Fig.1 Distribution of related geomagnetic station

表1 台站参数Table 1 The parameters of stations

表2 2011—2014年每年8月地磁数据Table 2 Geomagnetic data of 2011—2014 in August
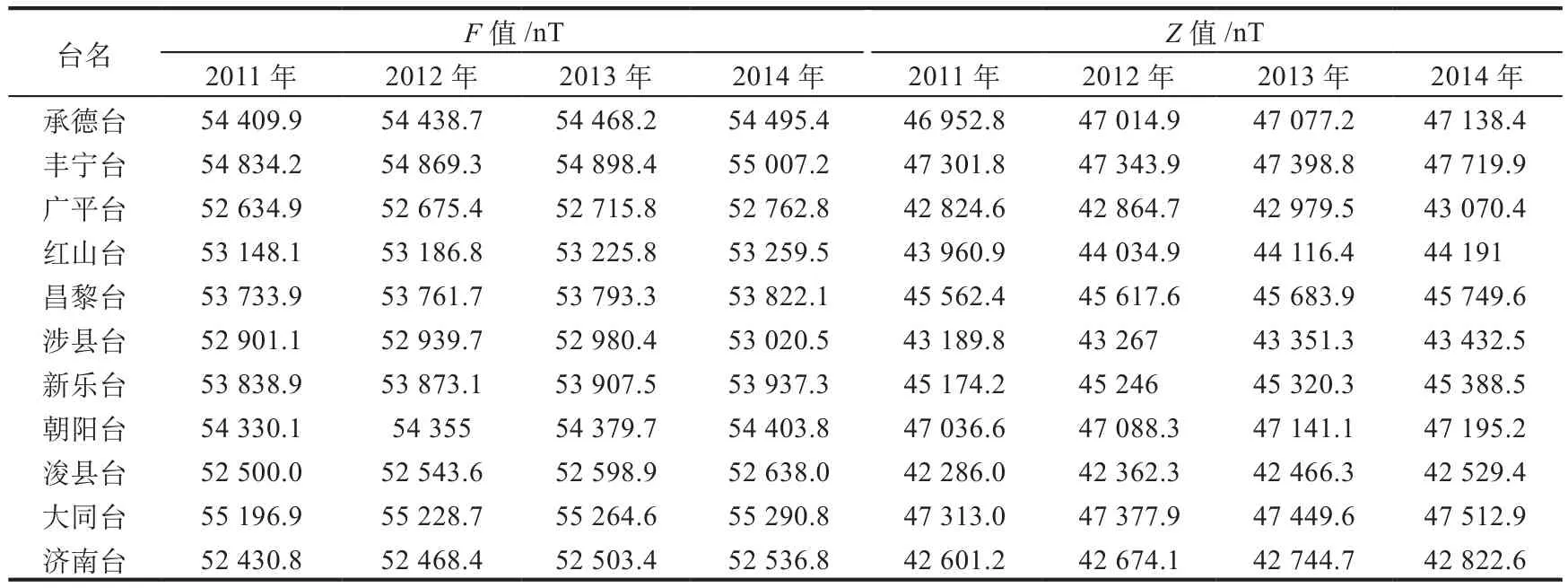
表3 2011—2014年每年12月地磁数据Table 3 Geomagnetic data of 2011—2014 in December
因所选11个地磁台站相距较远,地磁观测数据相差较大,为了直观对比各台数据变化,同轴绘制日均值曲线图。将2011—2014年每年8月和12月F、Z日均值减去该月的月均值,得到图2、图3。
由图2—图3可以看出:①2011—2014年,地磁扰动较大的每年8月,日均值曲线变化幅度较大,最大幅度约300 nT;地磁场相对平静的12月,日均值曲线变化幅度相对较小,变化范围基本在50 nT以内;②承德台、昌黎台地磁观测数据日变化幅度相对较小,其他台站相对较大;各地磁台观测数据变化幅度不同,长期变化趋势一致,能较客观记录并反映河北地区地磁场近期变化特征。
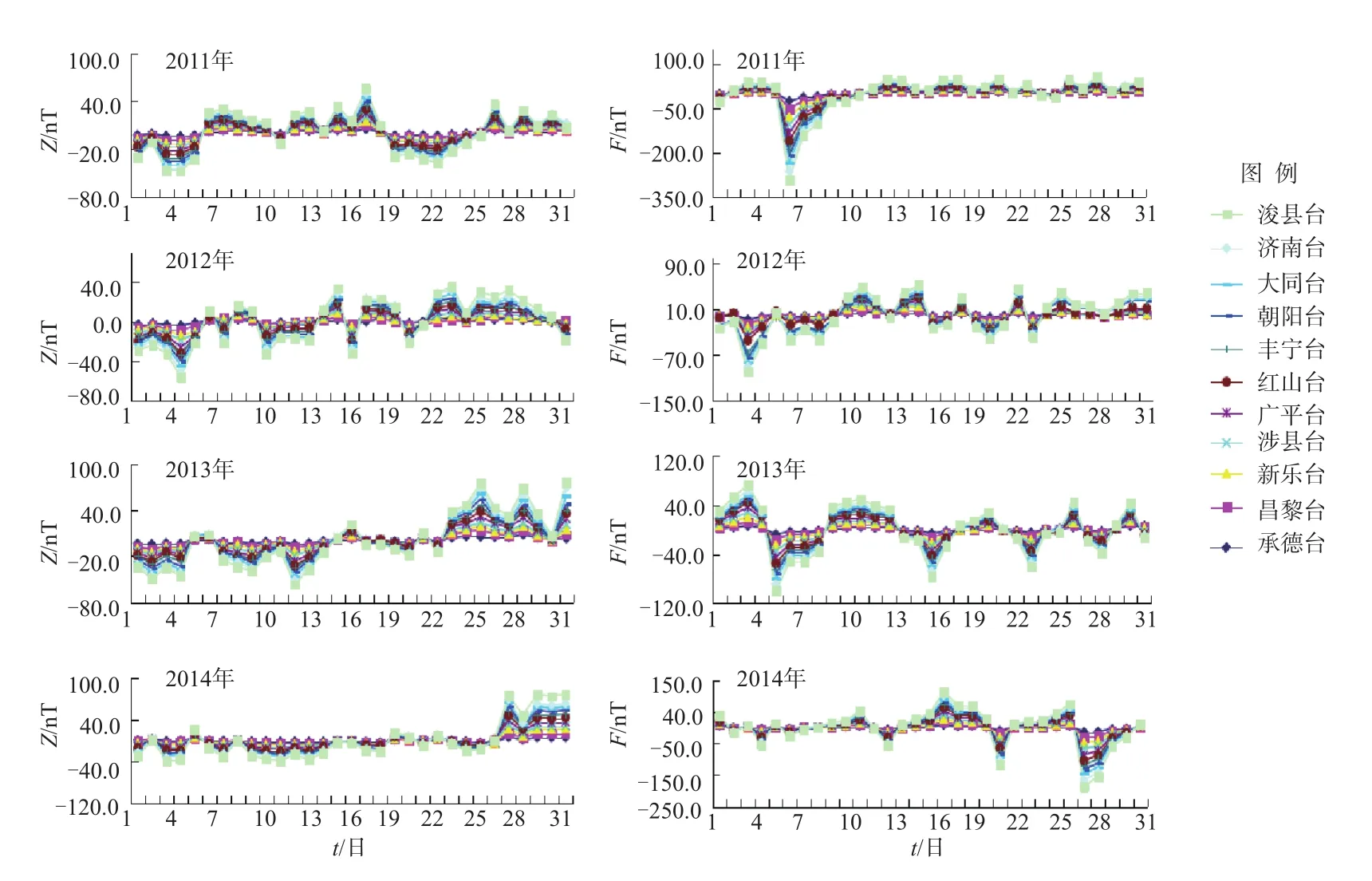
图2 2011—2014年每年8月各台F、Z日均值Fig.2 The daily mean value of F and Z of 2011—2014 in August
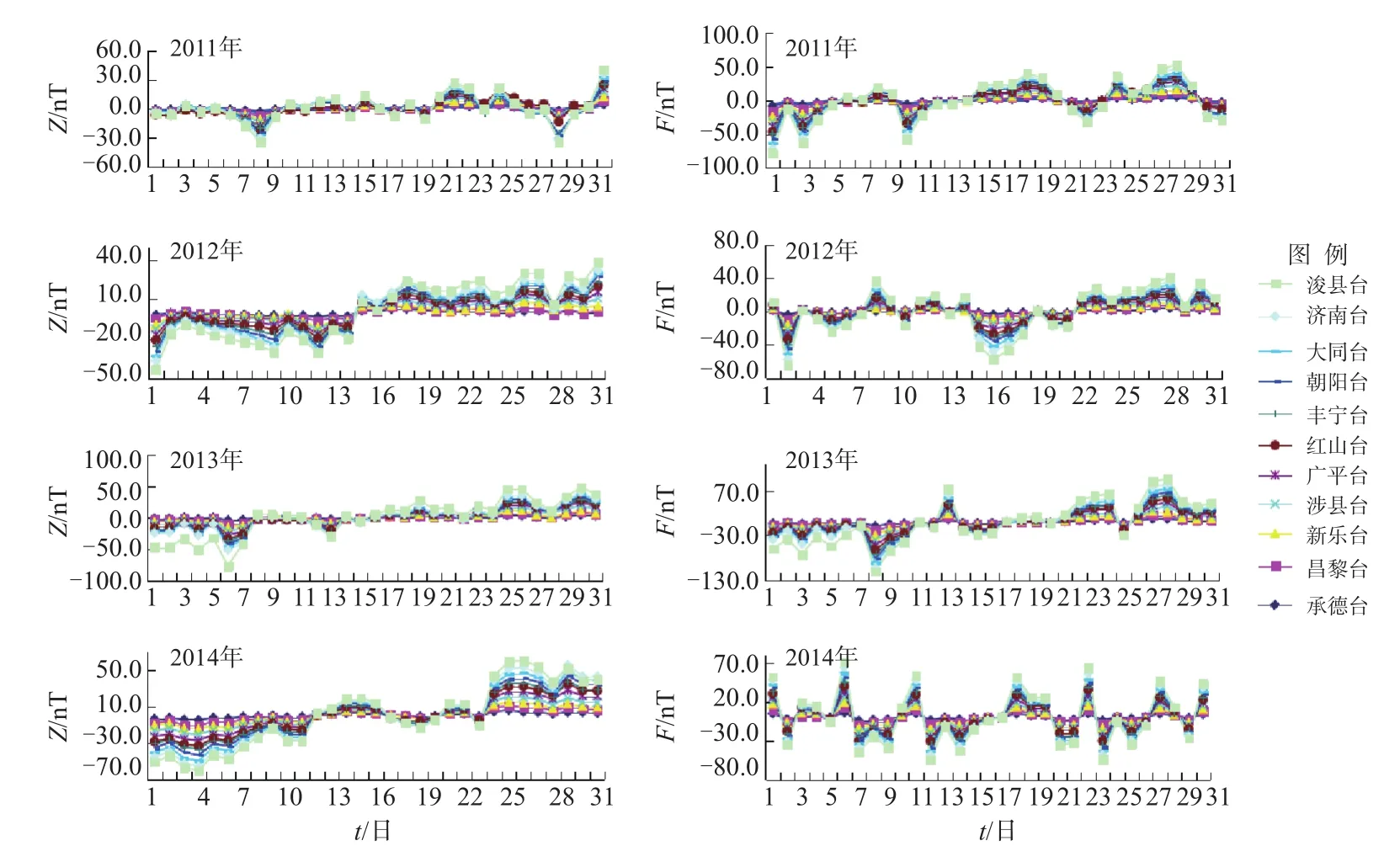
图3 2011—2014年每年12月各台F、Z日均值Fig.3 The daily mean value of F and Z of 2011—2014 in December
2 计算方法
地磁数据的观测和采样往往在不规则且离散的测网(或测线)进行。为合理并正确解释地球物理异常,在保持原有场特征前提下,有必要进行均匀且较密集规则网格的数据插值,形成直观的二维等值线,为进一步异常分析提供依据(刘强等,2013)。
常用格网化插值方法包括三角网线性内插方法、径向基函数法、最小曲率法、克里金法、反距离加权法和多项式拟合法等(唐泽圣,1999;王建等,2004;王广君等,2005)。反距离加权法缺点是,在格网区域内会产生围绕观测点的“牛眼”,给磁法数据解释带来不便(李富等,2009)。三角网线性内插方法仅用三角形的3个顶点线性内插出三角形内所有点的值,观测点分布稀疏情况下很难保证插值精度,一般适合于小比例尺的地层模型和断层(张琚等,2006)。径向基函数法、最小曲率法和多项式拟合法均属于平滑插值,一般不适合具有局部异常的磁法数据插值。当空间连续性变化的属性不规则时,克里金插值法能够在保持原有场特征前提下,更合理地对地球物理异常做出正确的解释(陈欢欢等,2007;江玉乐等,2007)。
局部地磁场中的地球主磁场、地磁异常场及扰动磁场与克里金法的3种成分假设具有一一对应关系:地球主磁场是局部地磁场中与恒定均值或趋势有关的结构性成分;地磁异常场为与空间变化有关的随机变量,而且地磁异常场满足二阶平稳假设;扰动磁场则可以视为与空间无关的随机磁场噪声。因此,克里金法能较为准确地反映局部地磁场的分布空间相关特性规律,可用于局部磁场空间插值(刘强等,2013)。
克里金法(Kriging)是由南非金矿工程师Krige D G 于1951年提出的一种空间插值方法,法国地质学家Dr Mathhemn在1962年加以完善,并以克里金命名,最早应用于矿产资源储量估算。该方法建立在变异函数理论分析基础上,对有限区域内的区域化变量取值进行无偏最优估计(best linear unbiased estimator,BLUE)。克里金法是线性的,因为其估计值是根据已有资料的加权线性结合获得的。与其他估计方法相比,克里金插值法的平均残差或误差接近于零,使误差方差最小是其显著特点。该方法与传统插值方法的不同之处在于,估计原观测样本数值时,不仅考虑待插值点与邻近观测数据点的空间位置,还考虑各邻近点之间的空间位置关系,而且根据已有观测数据空间分布的特点,使其估计比传统方法更加贴近实际。
克里金法的基本原理为:设研究区为A,点承载的区域化变量为Z(x,y)[Z(x,y)∈A]在采样点i(i=1,2,…,n)处的属性值为Zi(i=1,2,…,n),待插值点Z0的属性值插值结果是m个已知采样点属性值的加权和,即

式中:λi(i=1,2,…,m)为待确定权重系数。根据克里金原理,Z(x,y)在研究区内满足二阶平稳假设,即:①Z(x,y)的数学期望存在且等于常数,即E[Z(x,y)]=m;②Z(x,y)的协方差函数存在且相等(即只依赖于空间滞后距离h,而与位置无关),即
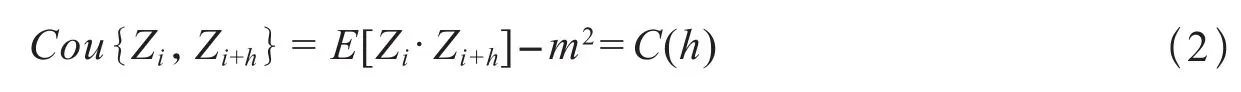
在无偏条件下使估计方差达到最小,经过推导得到权重系数的方程组。
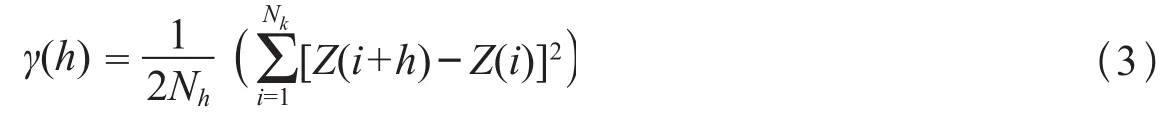
式中:μ为拉格朗日常数;γ(hi-hj)为样本点间的半变异函数值;γ(h0-hi)为已知点与待插值点间的半变异函数值。求出权重系数λi(i=1,2,…,m),即可求得待插值点属性值的估计值Z0。
克里金法的半变异函数定义为
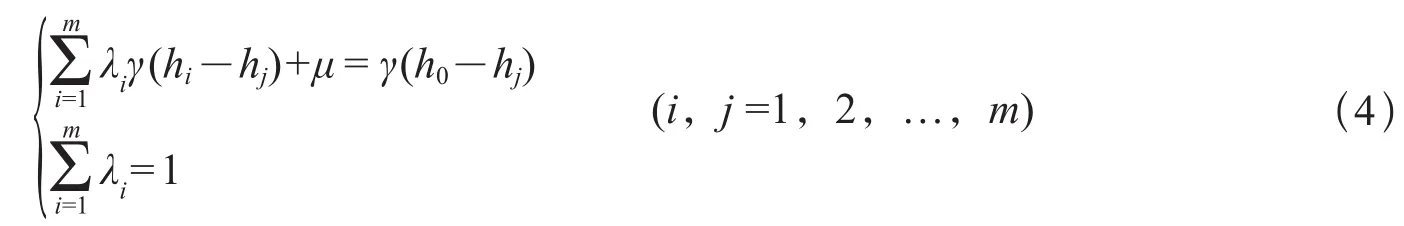
式中:h为上文提到的滞后距离;Nh是滞后距离数量;Nk是用来计算半变异函数值的距离为h的样本对数目;γ(h)表示半变异函数值只与h有关。由于距离为h的样本点对通常有很多个,通过公式(4)得到的半变异函数值与h是一对多的关系,据此拟合半变异函数的实际形式比较困难。通常做法是,选取一定步长来对点分组,分别计算每组的平均半变异值,通过选取合适的拟合模型拟合参数,得出半变异函数的确切函数形式,带入公式(3),求解待插值点的估计值。
3 资料分析
由于11个地磁台站海拔高程差异较大,插值前需对地磁观测数据进行高度改正。具体思路为:选定一个高度作为标准高度,选择相应经纬度作为计算点得出该地正常场,计算不同高度修正值,若台站海拔高于标准点,则实测值需要加上改正值;反之,减去改正值。利用surfer软件,对河北地区2011—2014年地磁资料应用克里金法进行插值计算,插值间隔为0.072×0.072,使x分成100个网格,而y分为82个网格,得到磁场总强度F和垂直分量Z的二维等值线和三维等值线。因2011—2014年地磁场总强度F和垂直分量Z的变化趋势基本一致,在此只给出2014年F、Z等值线图,见图4、图5。
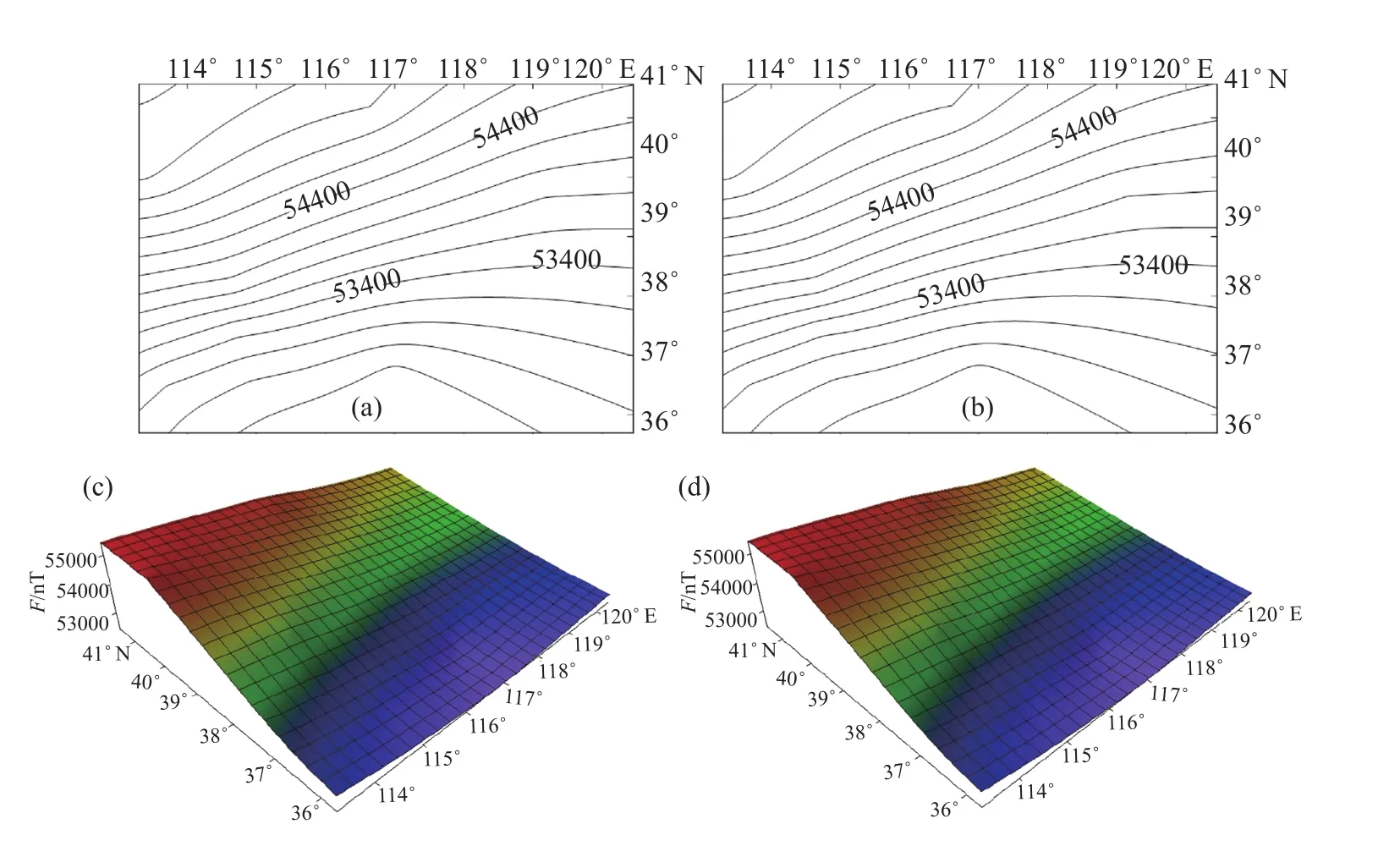
图4 2014年8月和12月地磁场总强度F二维、三维等值线(a) 2014年8月F值二维等值线;(b) 2014年12月F值二维等值线;(c) 2014年8月F值三维等值线;(d) 2014年12月F值三维等值线Fig.4 The 2D and 3D contour map of geomagnetic field total intensity F of 2014 in August and December
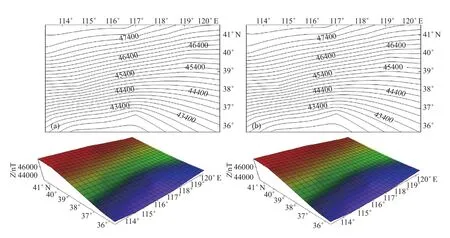
图5 2014年8月和12月地磁场垂直分量Z值二维、三维等值线(a) 2014年8月Z值二维等值线;(b) 2014年12月Z值二维等值线;(c) 2014年8月Z值三维等值线;(d) 2014年12月Z值三维等值线Fig.5 The 2D and 3D contour map of geomagnetic field vertical component Z of 2014 in August and December
为避免边界效应,只分析图形内部等值线变化。由图4可以看出:F值随纬度增加而增加;在(114°—116°E,37°—39°N)F变化率较大,(118°—120°E,36°—41 °N)变化率较小;(117°E,36.5°N)的F值较周围地区偏低,为该区极小值;(116.9°E,41°N)F值较周围地区偏高,为该区极大值;2011—2014年F变化趋势较平稳,由北向南呈减小趋势。
由图5可以看出:地磁场垂直分量Z的变化与F基本一致。Z值等值线与纬度基本平行,且绝对值随纬度的增加而增加。在(114°—116°E,37°—39°N)地磁场垂直分量Z变化率较大,(118°—120°E,36°—39°N)变化率较小;(117°E,36.5°N)的Z值较周围地区偏低,为该区极小值;(116.9°E,41°N)的Z值较周围地区偏高,为该区极大值;2011—2014年Z值变化趋势较平稳,由北向南呈减小趋势。
4 结论
根据上述资料处理结果可知,河北地区近期地磁场总强度F和垂直分量Z的变化具有抑下特征:①F值、Z值变化与纬度密切相关,且随纬度增加而增加,与经度关系较小;二者极大值均出现在(116.9°E,41°N)附近,而极小值出现在(117°E,36.5°N)附近,极大值与极小值经纬度位置经度差异不大,纬度存在较大差异;②F值、Z值随时间增加而增大,且呈逐年增大趋势,年增幅分别约为35 nT和70 nT,未发现趋势性变化;③F值、Z值分布与该区内台站分布状况有关。地磁台站比较集中在河北区的东北部和西南部,其等值线分布比较密集,而地磁台站分布较少的西北部和东南部等值线分布相对较离散;④本文在分析河北地区地磁场变化特征时,只对该区地磁场的日均值和月均值进行了相关研究,在今后工作中将进一步考虑地磁场的日变化、季节变化和年变化等特征。
上述对地磁场特征的讨论主要总结了地震活动较为平静时期的特点,在此基础上如果出现明显的地磁场变化,则应考虑地震发生的可能性。由于研究区域内地磁台站分布较少等原因,分析精度和深度都还不够,有待于今后更进一步工作。
陈欢欢,李星,丁文秀.Surfer 8.0等值线绘制中的十二种插值方法[J].工程地球物理学报,2007,4(1):52-57.
江玉乐,李才明,张朝霞.B样条分层离散插值在磁测异常处理中的应用[J].西南石油大学学报,2007,29(4):12-15.
李富,王永华.10种插值方法在物探数据处理中的对比——以电法和磁法资料中的应用为例[J].四川地质学报,2009,29(4):474-476.
刘强,陶钧,刘旭,等.基于克里金插值的磁法数据格网化研究[J].河南科学,2013,31(7):1 039-1 044.
唐泽圣.三维数据场可视化[M].北京:清华大学出版社,1999.
王广君,房建成.一种星图识别的星体图像高精度内插算法[J].北京航空航天大学学报,2005,31(5):566-569.
王建,白世彪,陈晔.地理信息制图[M].北京:中国地图出版社,2004.
薛革,陶九庆,张继红.山东地区地磁背景场的变化特征[J].高原地震,1995,7(4):50-54.
解用明.河北省近年地磁Z分量长期变特征[J].山西地震,1996,2:47-50.
张琚,李星.利用IDL进行地学数据处理的多种插值法[J].工程地球物理学报,2006,3(1):49-53.
张小涛,王莉森,韩丽萍.河北省近年内地磁场变化规律的初步分析[J].地震地磁观测与研究,2008,29(6):17-21.
Abstract
By using the method of Kriging,the paper analyzed and calculated the total intensity F value and vertical component Z value from the year 2011 to 2014 in Hebei Province,and the authors finally got the variable features of geomagnetic field in Hebei area.The results showed that the variation of the geomagnetic background field closely related to the change of geographic latitude and no relationship with the change of geographic longitude;the distribution of isogram of the F and Z values was relation with the distribution of the geomagnetic stations,the values of F and Z were larger with the time.
The analysis of the variable features of geomagnetic field in Hebei area by using the method of Kriging
Dong Bo1),2),Ji Chunling1),Zhang Huanxi1),Li Feng1),Zhou Anpin1),Niu Shuyu1),Zhao Yuchen1),Liu Jing1),Liu Tan1)and Zhu Yinjie1)
1) Earthquake Administration of Hebei Province,Shijiazhuang 050021,China
2) Hebei GEO University,Shijiazhuang 050021,China
geomagnetic field,Kriging,isogram
10.3969/j.issn.1003-3246.2016.03.025
董博(1986—),男,助理工程师,主要从事地震监测与异常跟踪分析工作。E-mail: dongbo0002@126.com

