基于mexh小波变换的门式框架裂纹识别定位研究
詹化军 朱 检
(1.湖南省第五工程有限公司,湖南 长沙 410000; 2.中建五局装饰幕墙有限公司,湖南 长沙 410000)
基于mexh小波变换的门式框架裂纹识别定位研究
詹化军1朱 检2*
(1.湖南省第五工程有限公司,湖南 长沙 410000; 2.中建五局装饰幕墙有限公司,湖南 长沙 410000)
以杭长铁路客专湖南段站房工程中某平面框架为研究对象,将裂纹模拟为带半椭圆形片状的表面裂纹,计算了三种框架损伤工况模型,通过数值计算,验证了裂纹定位识别方法的正确性与有效性。
平面框架,非贯通表面裂纹,损伤识别,转角模态,小波变换
一直以来,复杂结构的损伤定位是损伤识别领域的热点问题,但多数研究均针对梁或柱的杆件结构,而关于带有非贯通表面裂纹的平面框架损伤定位的文献鲜有报道。Quan Wang[4]比较了在集中荷载作用下无损伤简支梁与含裂纹的简支梁的挠度,并通过小波变换中多尺度分析来识别损伤。Ovanesova等[5]基于动力参数对在支座和梁柱固结节点附近含有损伤的平面框架进行小波变换损伤识别与诊断。Huang等[6]采用基于连续小波变换方法对三层非对称框架结构振动响应识别结构的损伤。Hera等[7]基于动力参数与有限元研究了四层钢框架结构的损伤识别问题,再选取db4小波对研究节点的动力响应信号进行小波变换,进而定位钢框架结构的损伤。蒋欣[8]基于转角模态小波变换识别对铁木辛柯梁损伤定位进行识别。
本文针对平面门式框架中的不均匀非贯通表面裂纹,以杭长铁路客专湖南段站房工程为研究背景,取某单层平面框架为计算对象,分别建立了三种框架损伤工况模型(梁含有一条裂纹、柱各含有一条裂纹、梁和柱各含有一条裂纹),经由mexh小波变换后得到其小波系数模极大值来识别框架损伤位置。并对比转角模态与基本振型小波变换的框架损伤定位识别结果,从而验证了本文方法的有效性与可行性。
1 损伤识别基本理论
1.1 小波奇异性原理

(1)
其中,Ψa,b(t)为小波函数;a,b分别为尺度、平移因子,即小波窗沿时间轴移动过程中其窗口大小、形状固定可以时刻变化。Ψ(t)为母小波满足以下允许条件:
(2)
可见,母小波具有两个特性:1)局部性;2)震荡性。

(3)
可见,小波变换模极大值|Wf(s,u)|为对应信号f的突变点[8]。在信号突变点处小波系数的绝对值比较大,即可通过检测模极大值点来识别信号中奇异点的位置。
为了精确快速地检测损伤信号中的奇异点,所选小波基应满足如下4个特性:1)紧支性;2)消失矩;3)正则性;4)对称性。
本文选取mexh小波(又称为墨西哥帽小波)对门式框架的模态参数(基本振型和转角模态)进行分析。其中,mexh函数为Gauss函数的二阶导数:
(4)
该函数消失矩为2,满足上述4个条件。
1.2 裂纹定位识别方法
以往的研究表明[9]:在研究含横向贯通损伤构件(如梁或柱)的抗弯刚度时,可采用减小构件横截面高度后的刚度来代替损伤所对应截面的抗弯刚度。而本文对于框架中的非贯通表面裂纹的模拟采用有限元实际模拟,为了简化裂纹模型其尽可能与实际相联系,将裂纹外形模拟为半椭圆形片状。
由文献[8]的研究成果表明:损伤位置的转角的相对变化量却很显著且更为连续,对于小波分析可采用转角模态信号则更容易反映出结构的损伤位置,自动过滤几何突变造成的其他参数信号变化,可避免出现损伤误判的问题。
2 数值算例
为了验证以上识别方法的正确性,以杭长铁路客专湖南段站房工程为研究背景,取工程中的A区4号框架结构为研究对象,立柱的支座固结于大地的平面门式框架,横梁BC与立柱AB,CD均为矩形等截面直杆,其中,柱AB,CD与梁BC长度均为1 200 mm,截面尺寸为h×b=(40×30)mm,材料为钢材Q235,弹性模量E=2.07×1011N/m2,密度ρ=7 800 kg/m3,泊松比μ=0.3。框架的尺寸及荷载作用位置如图1所示。框架中裂纹为半椭圆形片状的表面裂纹,裂纹的长短轴的尺寸分别为w=20 mm,v=10 mm,如图2所示。
本文共分析了框架中的三种损伤工况:第一,框架中横梁BC含有一条非贯通裂纹;第二,框架中两根立柱AB,CD均含有一条非贯通裂纹;第三,框架中横梁BC与立柱AB均含有一条非贯通裂纹。
首先,利用通用有限分析软件ANSYS建立梁的三维有限元模型,将框架的横梁与立柱3个杆件各离散为2 400个单元,框架中各单元由A→B→C→D的顺序依次编号为1~7 200,然后运用Lanczos法进行模态分析,求得其模态参数(基本振型与转角模态参数)。

2.1 框架结构含有一条裂缝
在框架节点B上作用x方向荷载100 kN,在梁的跨中作用y方向荷载600 kN,假设在距框架B节点1/3处有一条非贯通裂纹,其参数如上。分别对此工况下的基本振型和转角模态信号进行mexh小波变换,得到尺度为1时的小波系数图(见图3,图4)。

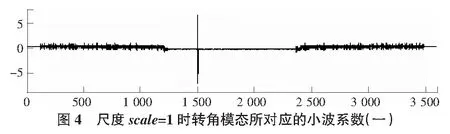
由图3,图4分析可得:以基本振型为损伤判别指标时,在尺度1上的小波系数(见图3)中有许多不规则的凸起,并且出现了两处非常大的小波系数数值,经分析,这两处是框架几何形状突变点,而非裂纹位置,即出现损伤误判现象。同时在距B节点1/3处裂纹位置并未出现明显的突变,说明基本振型小波变换方法难以准确识别框架裂缝所在位置。以转角模态为损伤判别指标时,在梁与柱刚接处小波系数无明显变化(见图4),而在其他位置出现了小波系数的模极大值,经分析表明此处为裂纹所在位置。
2.2 框架结构含有两条裂缝
1)梁BC与柱CD各带有一条裂缝。在框架左柱距A支座2/3处和在框架右柱距B支座1/2处各有一条非贯通裂纹,参数如上,框架受到同样的荷载作用。计算得到尺度为1时的小波系数图(如图5,图6所示)。
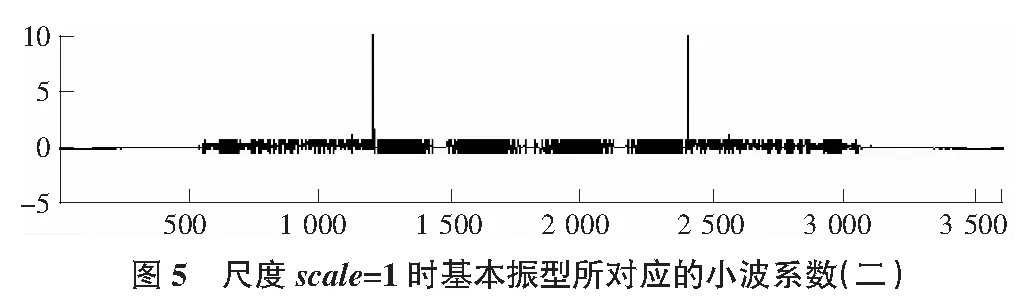

由图5,图6分析可得:图5在尺度1上的基本振型小波系数,在框架几何形状突变点处出现信号奇异点,此处的小波系数大于真实损伤位置的小波系数,即误判为损伤位置,无法定位损伤。而在图6中发现,梁柱固结点没有出现较大的小波系数,而分别在梁与柱的损伤处都出现了小波系数的模极大值,即对应着裂缝所在的位置。
2)梁BC与柱AB各带有一条裂缝。在同一工况下,分别在左柱距A支座2/3处和框架梁距C节点1/3处上各有一条同样几何参数的非贯通裂纹。计算得到尺度为1时的小波系数图(如图7,图8所示)。


由图7,图8分析可得:图7在尺度1上的基本振型小波系数,认为框架的几何形状突变处出现信号奇异点,且该位置的小波系数大于真实损伤位置的小波系数,即出现损伤误判的现象,无法定位框架中的损伤。而图8在尺度1上的转角模态对应的小波系数图中发现了两个明显的奇异点,且与图7中的奇异点位置不一致,说明图8中可找到实际损伤位置。
3 结语
1)建立了通过有限元ANSYS进行模态分析,以转角模态为结构损伤定位的判别指标,经由mexh小波对框架的转角模态信号进行小波变换后,由所得的小波系数模极大值点判别信号的奇异性,根据奇异点定位框架的裂纹,并通过数值算例验证了本文方法的可行性与正确性。
2)当仅以基本振型为损伤判别指标时,通过小波分析对三种损伤工况下平面框架进行损伤识别,发现在几何结构不连续处(即梁与柱固结位置)且无损伤时,出现该位置的小波系数模最大值大于实际损伤位置,即出现损伤位置误判的结果。对比实际损伤位置,可能存在梁柱连接处的小波系数比实际损伤位置明显,说明本文识别平面框架的损伤时存在一定的局限性。
3)为了避免由于几何形状突变导致的奇异性干扰,采用转角模态为损伤判别指标,针对该指标进行小波变换方法识别平面框架的损伤,对损伤的识别非常敏感,且其奇异性特征也十分明显。该判别指标可消除一些几何突变的节点。由于实际工程中非常难以获取转角模态实测值,但针对存在天然不连续的结构损伤定位识别应用具有理论指导意义。
[1] D.Liu,H.Gurgenci,M.Veidt.In Situ Damage Detection in Frame Structures through Coupled Response Measurements[J].Mechanical Systems and Signal Processing,2004,18(3):573-585.
[2] M.F.Elkordy,K.C.Chang,G.C.Lee.A Structural Damage Neural Network Monitoring System[J].Microcomputers in Civil Engineering,1994(9):83-96.
[3] P.G.Nikolakopoulos,D.E.Katsareas,C.A.Papadopoulos.Crack identification in frame structures [J].Computers & Structures,1997,64(14):389-406.
[4] Quan Wang,Xiaomin Deng. Damage Detection with Spatial Wavelets[J].International Journal of Solids and Structures,1999(36):3443-3468.
[5] A.V.Ovanesova,L.E.Suárez.Applications of Wavelet Transforms to Damage Detection in Frame Structures[J].Engineering Structures,2004,26(1):39-49.
[6] C.S.Huang,W.C.Su.Identification of Modal Parameters of a Time Invariant Linear System by Continuous Wavelet Transformation [J].Mechanical Systems and Signal Processing,2007,21(4):1642-1664.
[7] Adriana Hera,Zhikun Hou.Application of Wavelet Approach for ASCE Structural Health Monitoring Benchmark Studies [J].Journal of Engineering Mechanics,2004,130(1):96-104.
[8] 管德清,蒋 欣.基于小波分析的Timoshenko梁裂缝识别研究[J].振动与冲击,2007,26(5):67-70.
[9] 孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005.
Research on portal frame crack identification and localization based on mexh wavelet transform
Zhan Huajun1Zhu Jian2*
(1.HunanFifthEngineeringLimitedCompany,Changsha410000,China; 2.ChinaFifthConstructionGroup,DecorationCurtainWallLimitedCompany,Changsha410000,China)
Taking a plane frame in Hang-Chang railway passenger dedicated Hunan station section engineering as the research object, made the crack simulation of surface crack with semi elliptical, calculated the three damaged frame design model, through the numerical simulation, verified the correctness and effectiveness of crack location and recognition method.
plane frame, non penetrating surface crack, damage identification, corner mode, wavelet transform
1009-6825(2016)24-0043-03
2016-06-12
詹化军(1982- ),男,硕士,工程师
朱 检(1990- ),男,硕士
TU317.5
A

