紫外分光光度法测定陶瓷材料及制品中氧化钛含量的不确定度评价

张永财，朱守丹

（辽宁省轻工产品质量检测院，沈阳　110032）



Research&Discussion
研究与探讨

紫外分光光度法测定陶瓷材料及制品中氧化钛含量的不确定度评价

张永财，朱守丹

（辽宁省轻工产品质量检测院，沈阳110032）

本文利用紫外分光光度法对陶瓷材料及制品化学分析中的氧化钛含量进行了测定，对测量结果进行不确定度分析与评价。通过不确定度分析，找出不确定度的主要来源，计算出合成不确定度及扩展不确定度。

紫外分光光度法；不确定度；陶瓷材料及制品；氧化钛

1　引言

《检测和校准实验室能力的通用要求》规定，检测实验室应开展测量不确定度评定工作，当检测结果临近临界值时，测量不确定度分析评定是检测工作的重要技术组成部分。不确定度表示在实验测量结果中，由于测量误差的存在，而对被测量值不能确定的程度，表示被测量的真值存在于某一个量值范围的评定，它反映了测量结果的可信程度的高低。

检测陶瓷材料及制品中氧化钛含量是陶瓷材料及制品化学分析中的主要检测项目，紫外分光光度法是目前测定陶瓷材料及制品中氧化钛含量的常用方法。本文结合实际工作，依据相关技术标准和文件，对紫外分光光度法测定陶瓷材料及制品中氧化钛含量的不确定度进行了评定，建立数学模型分析不确定度的主要来源，计算出合成不确定度及扩展不确定度。

2　测量方法

2.1主要仪器与试剂

本实验所采用的主要仪器和试剂有：紫外分光光度计，型号：UV-1801（北京瑞丽分析仪器公司）；电子分析天平，型号AEG（日本岛津）精度±0.0001 g；铂皿；50 mL、100 mL、250mL、1000mL等容量瓶；10mL、25mL等移液管；水为二次去离子水；其它试剂均为优级纯或分析纯。

2.2测量步骤

按照GB/T4734陶瓷材料及制品化学分析方法中碱熔试样的方法制备试液。分取试液20.0mL，摇匀，加入盐酸（1+1）7mL，二安替比林甲烷溶液（6%）8 mL，用水稀释到刻度，摇匀。放置1 h后，以试剂空白为参比，在分光光度计上，于波长390 nm处，用2 cm比色皿，测其吸光度。并在标准曲线上查出相应的二氧化钛的浓度。

3　不确定度的来源分析

3.1数学模型

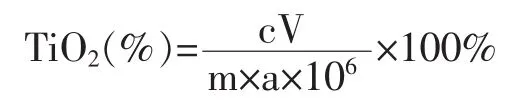
式中：c—在标准曲线上査得氧化钛浓度，mg/mL；

V—试液的体积，mL；

m—试剂质量，g；

a—分取试剂的体积与总体积之比。

3.2不确定度的来源分析

紫外分光光度法测定陶瓷材料及制品中TiO2含量不确定度的来源很多，从实际工作出发，我们主要研究对不确定度影响显著的几个主要因素。

（1）测量重复性引入的相对标准不确定度。

（2）标准曲线最小二乘法拟合引入的不确定度。

（3）配制标准溶液引入的相对标准不确定度。

（4）试样溶液的制备引入的相对标准不确定度。

4　TiO2测量不确定度的评定

4.1测量重复性引入的相对标准不确定度urel（算）

用同一标准溶液校正仪器，对同批陶瓷材料及制品化学分析中氧化钛含量进行6次平行检测，以其检测结果为考察对象，这些数据均符合GB/T176-2008中允许误差范围的要求，测定结果如表1所示。

表1　同批次陶瓷材料试样检测TiO2的测定结果（n=6）

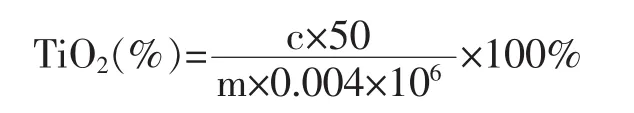
单次测量的不确定度：

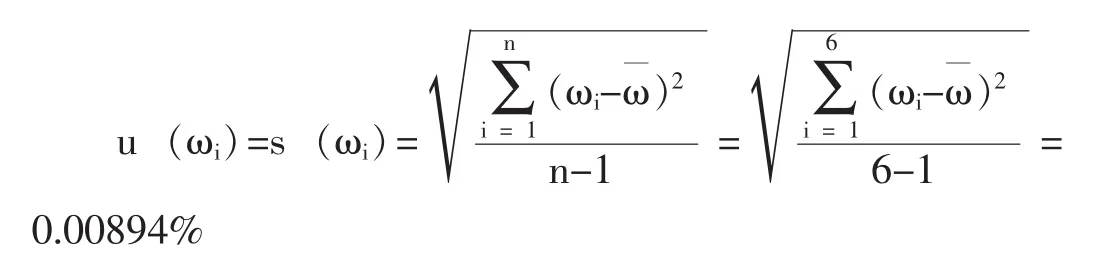
算术平均值的不确定度：

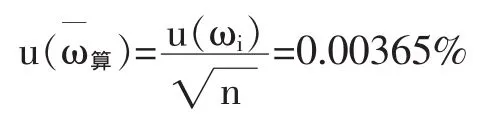
因此，由测量重复性引入的相对标准不确定度为：

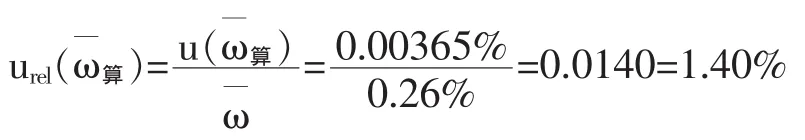
4.2标准曲线最小二乘法拟合引入的不确定度

最小二乘法拟合标准曲线校准产生的不确定度，直线拟合为最常见、最简单的一种，它给出两个变量C、y间的线性关系。通过测量出一组数据（Ci，yi），（i=1,2…n），得到的一条直线y=a+bC，所有这些点（Ci，yi）与这条直线垂直距离之差的平方和为最小，这就是所谓的最小二乘法。

4.2.1拟合过程

采用7个浓度水平的标准溶液，用紫外分光光度计测定，得到相应的吸光度y，用最小二乘法进行拟合，得到直线方程和相关系数。氧化钛质量浓度-吸光度结果如表2所示。

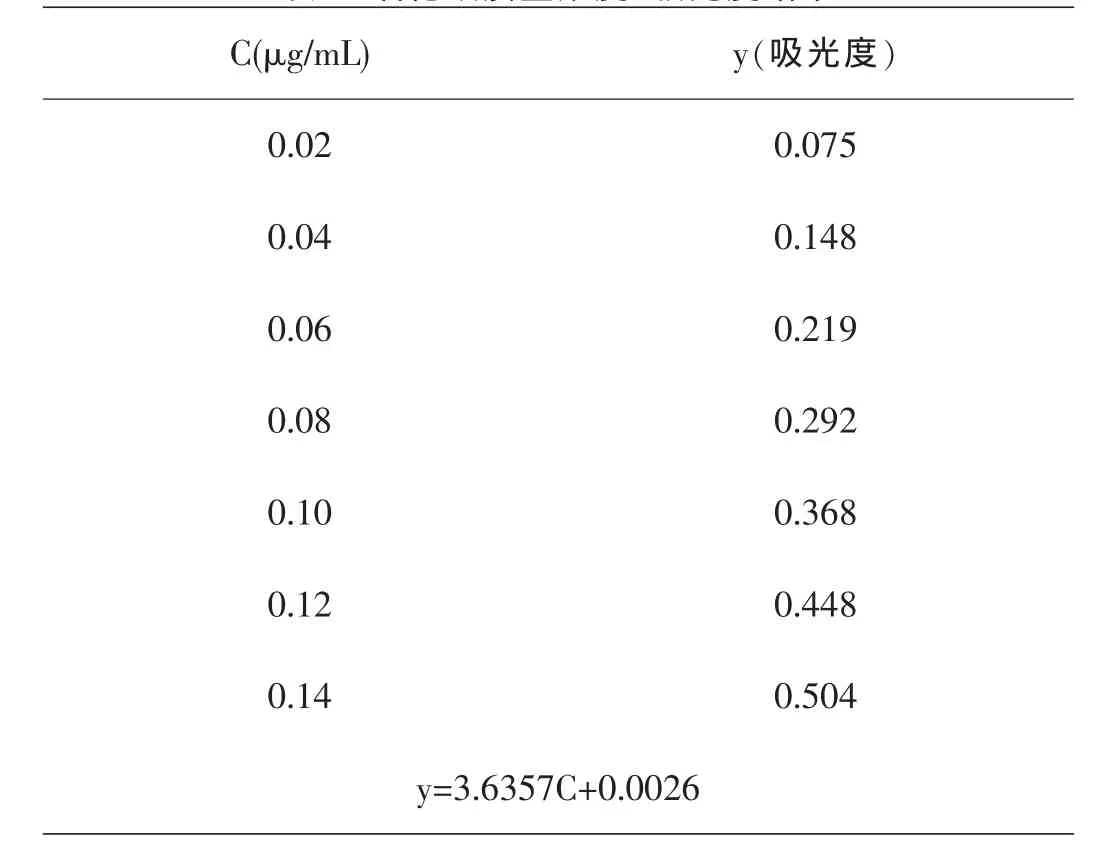
表2　氧化钛质量浓度-吸光度结果

直线方程：y=a+bC

式中：a：为直线截距；

b：为直线斜率，也称回归系数。

4.2.2由标准曲线拟合带来的标准不确定度

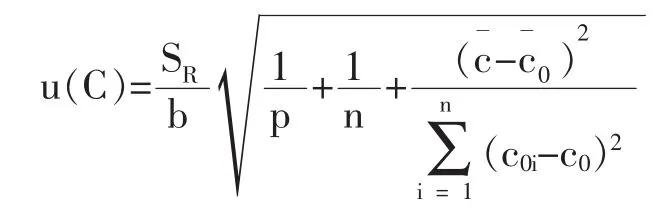
SR：回归曲线的剩余标准差（残差的标准差）

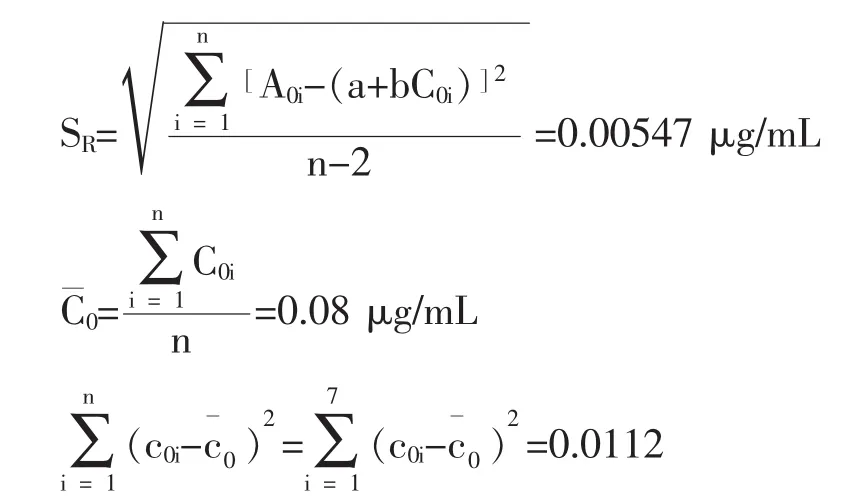
则由标准曲线拟合带来的不确定度：

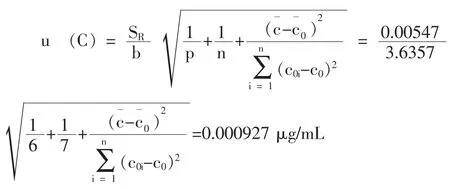
4.2.3标准曲线校准带来的相对不确定度

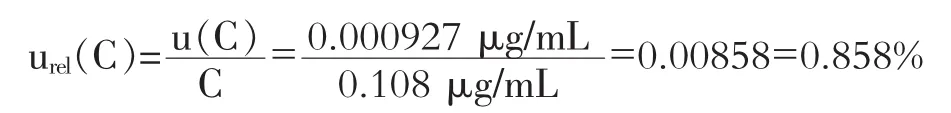
4.3配制标准溶液引入的相对标准不确定度urel（x1）

4.3.1标准物质称量过程中引入的不确定度

由天平检定证书可知其不确定度为：0.4mg，按均匀分布计算，则标准不确定度为：

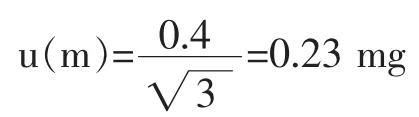
按称样量0.1000 g计算，则：

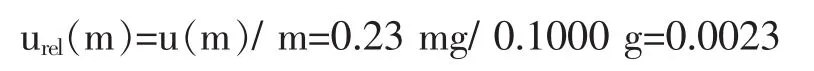
4.3.2基准试剂TiO2纯度（PTiO2）引入的不确定度

供应商证书上给出的PTiO2值为100%±0.05%，其引入的不确定度可考虑为矩行分布，标准不确定度为：

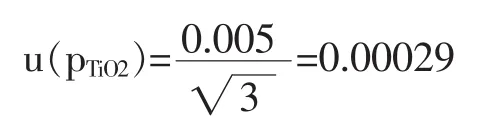
其相对不确定度为：

4.3.31000m L容量瓶引入的不确定度

（1）1000mL容量瓶，其检定证书提供的扩展不确定度为0.4mL，按均匀分布计算，则校准所引入的标准不确定度为：

（2）使用温度与校正温度之间的差异会引入不确定度分量，水的膨胀系数为2.1×10-4℃，假定校正温度与使用温度的差异为±3℃，则校准所引入的标准不确定度为：

按均匀分布计算，其标准不确定度为：

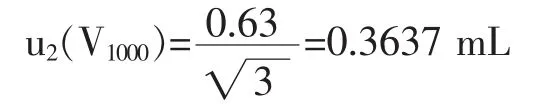
则1000mL容量瓶引入的不确定度为：

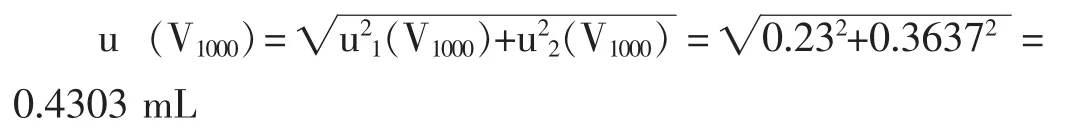
相对不确定度为：

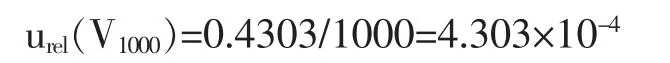
4.3.4100m L容量瓶引入的不确定度

1）本实验所用的100 mL容量瓶，其扩展不确定度为0.10 mL则：

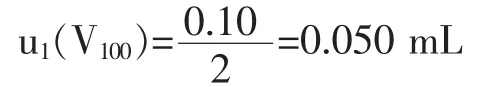
2）使用温度与校正温度之间的差异会引入不确定度分量，水的膨胀系数为2.1×10-4℃，假定校正温度与使用温度的差异为±3℃，则校准所引入的标准不确定度为：

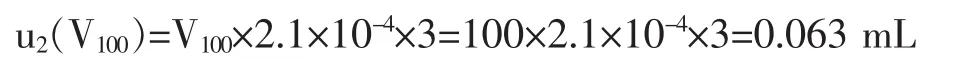
按均匀分布计算，其标准不确定度为：

则100mL容量瓶引入的不确定度为：

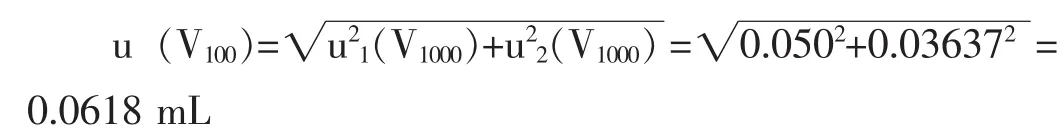
相对不确定度为：

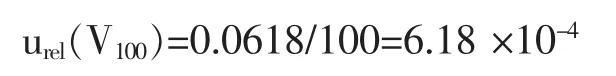
4.3.5250m L容量瓶引入的不确定度

1）本实验所用的250 mL容量瓶，其扩展不确定度为0.15 mL则：

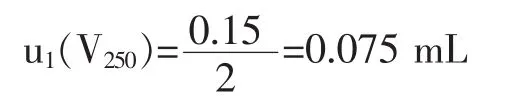
2）使用温度与校正温度之间的差异会引入不确定度分量，水的膨胀系数为2.1×10-4℃，假定校正温度与使用温度的差异为±3℃，则校准所引入的标准不确定度为：

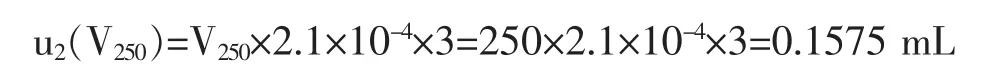
按均匀分布计算，其标准不确定度为：

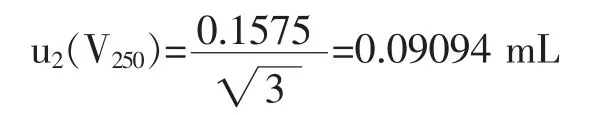
则250mL容量瓶引入的不确定度为：

相对不确定度为：

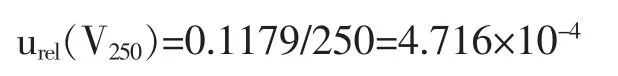
4.3.6标准溶液稀释引入的不确定度

从氧化钛标准溶液（1 mg/mL）中用10 mL移液器分别移取 1.0 mL、2.0 mL、3.0 mL、4.0 mL、5.0 mL、6.0 mL、7.0mL分别置于7个50mL容量瓶中，用水稀释至刻度，摇匀。此系列标准溶液氧化钛浓度分别为0.02 mg/mL, 0.04mg/mL,0.06mg/mL，0.08mg/mL，0.10mg/mL，0.12 mg/ mL，0.14mg/mL。

（1）稀释过程移液器引入的不确定度

本实验所用的A级10 mL移液器允差为0.020 mL，按三角分布考虑，包含因子则10mL移液器的不确定度为：

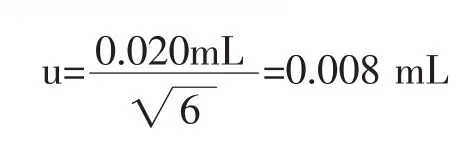
1）移取1mL氧化钛标准溶液配制0.02 mg/mL标准溶液的相对不确定度

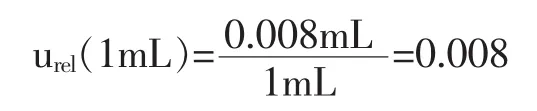
2）移取2mL氧化钛标准溶液配制0.04mg/mL标准溶液的相对不确定度

3）移取3mL氧化钛标准溶液配制0.06mg/mL标准溶液的相对不确定度

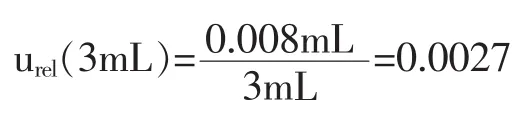
4）移取4mL氧化钛标准溶液配制0.08mg/mL标准溶液的相对不确定度

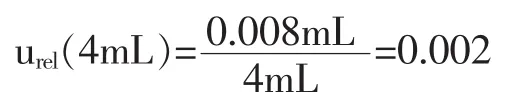
5）移取5mL氧化钛标准溶液配制0.10 mg/mL标准溶液的相对不确定度

6）移取6mL氧化钛标准溶液配制0.12 mg/mL标准溶液的相对不确定度

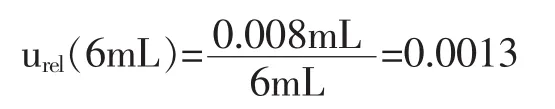
7）移取7mL氧化钛标准溶液配制0.14 g/mL标准溶液的相对不确定度

则氧化钛标准溶液稀释过程中，移液器引入的不确定度为：

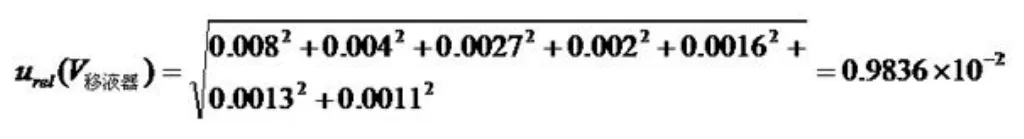
（2）50mL容量瓶引入的不确定度

1）本实验所用的50 mL容量瓶，其扩展不确定度为0.05mL则：

2）使用温度与校正温度之间的差异会引入不确定度分量，水的膨胀系数为2.1×10-4℃，假定校正温度与使用温度的差异为±3℃，则校准所引入的标准不确定度为：

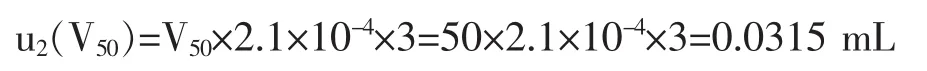
按均匀分布计算，其标准不确定度为：

则50mL容量瓶引入的不确定度为：

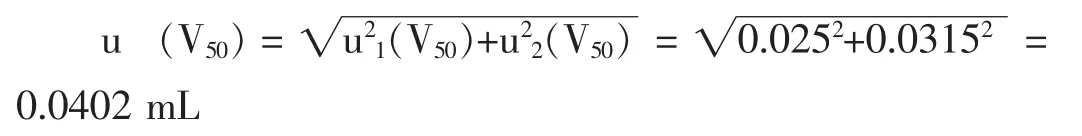
相对不确定度为：

因此，配制标准溶液引入的相对标准不确定度为：

4.4试样溶液的制备引入的相对标准不确定度Urel（X2）

4.4.1称量引起的不确定度

称量引入的不确定度主要来源于称量操作的不确定度。由天平检定证书可知其不确定度为：0.4mg，按均匀分布计算，则标准不确定度为：

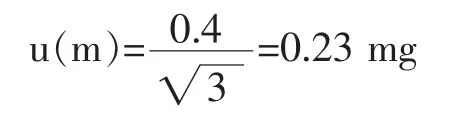
按称样量0.5216 g计算，则：

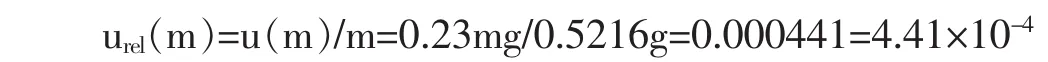
4.4.2250m L容量瓶引入的不确定度

本实验所用的250 mL容量瓶，其扩展不确定度为0.15mL，则同4.3.5相对不确定度为：

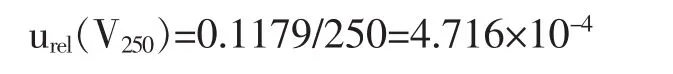
4.4.3移取1m L氧化钛试样溶液相对不确定度

移取1mL氧化钛试样溶液相对不确定度同4.3.6 1）相对不确定度为：

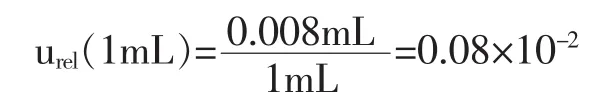
4.4.450m L容量瓶引入的不确定度

50mL容量瓶引入的不确定度，同4.3.6（2）相对不确定度为：

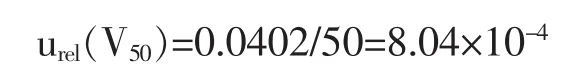
因此，由试样溶液制备所引入的相比标准不确定度为：

4.5合成不确定度及扩展不确定度

由于上述个测量不确定度分量之间无相关关系，所以实验结果的合成相对标准不确定度为：

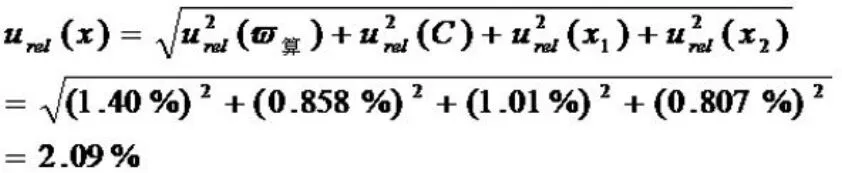
合成标准不确定度：

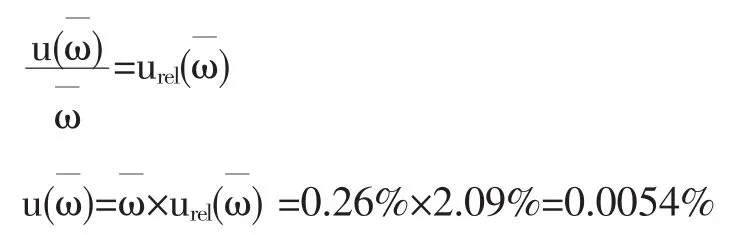
4.6扩展不确定度及测量结果表示

取包含因子k=2，可求得扩展不确定度U（x）。

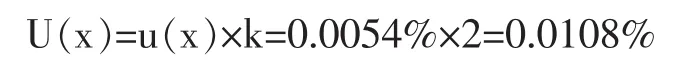
5　测量结果

在报告氧化钛含量的测量结果时，给出不确定度值，结果表示如下：

在实际检测中应规范操作，尽可能降低不确定度，增强检测数据的可靠性。

［1］国家质量技术监督局.测量不确定度评定与表示（JJF1059.1-2012）［S］.北京：中国计量出版社，2012.

［2］中国实验室国家认可委员会.化学分析中不确定度评定与表示指南［S］.中国计量出版社，2002.