整流罩分离计算方法研究

顾名坤，张 鹭，吴 洁，贺元军，刘立东

（1.北京宇航系统工程研究所，北京100076；2.中国载人航天工程办公室，北京100720）

整流罩分离计算方法研究

顾名坤1，张 鹭1，吴 洁1，贺元军2，刘立东1

（1.北京宇航系统工程研究所，北京100076；2.中国载人航天工程办公室，北京100720）

针对传统的效能系数计算方法存在的无法准确预示飞行状态整流罩分离运动的不足，以典型的旋抛整流罩为研究对象，提出了一种将全部因素作为计算变量的多因素计算方法，建立了整流罩分离动力学方程，论述了每个变量的获取方法，在地面大气环境中采用某型号真实整流罩，开展了分离试验，获取了罩内负压特性和分离运动参数，计算结果与试验结果一致性较好。相对于传统的效能系数计算方法，多因素计算方法更加准确，对指导整流罩分离系统方案设计更加有效，具有显著的工程应用价值。

整流罩分离；多因素；负压特性；摩擦力

1　引言

整流罩分离系统是运载火箭的一个关键子系统，用于在运载火箭穿过大气层的预定时刻实现整流罩与箭体分离。整流罩分离仿真计算的准确性是整流罩分离系统设计的前提，整流罩分离地面试验是验证分离系统设计正确性的重要途径。

分离地面试验在大气环境中开展时，气动力的影响使分离试验的仿真计算较为复杂。使用LS-DYNA软件采用流固耦合算法可计算空气动力对整流罩分离过程的影响规律［1］，但是计算时间较长。另外，铰链摩擦力、纵向分离面挡风板的摩擦力、整流罩弹性特性等均会影响分离运动。整流罩弹性特性对整流罩分离安全间隙影响较大，但是对过顶角速度等运动参数的影响较小［2］。工程实践中，一般将摩擦力、弹性影响等折算为分离能源效能系数［3-5］，但是对于不同尺寸的整流罩、不同的分离能源、不同的分离方案，需要通过地面试验确定相应的效能系数，而且地面试验修正过的效能系数对飞行状态整流罩分离的计算误差较大，不能准确有效地指导工程设计。

整流罩分离方案普遍采用铰链约束式旋转分离方式，分离能源普遍采用分离弹簧。本文以采用分离弹簧作为分离能源的旋抛整流罩为研究对象，通过对地面分离试验测量结果的研究，提出一种精确高效的分离计算方法（简称多因素计算方法），用于指导整流罩分离系统设计，预示分离运动结果。

2　整流罩分离计算方法

2.1 整流罩地面分离试验计算方法

地面大气环境中开展整流罩分离试验时，作用于整流罩的外力有：分离弹簧推力、罩内负压、罩外动压、纵向分离面挡风板摩擦力和铰链摩擦力［3］。相对于传统的效能系数方法，为了更加直观、精确的描述各影响因素对整流罩分离运动的影响，本文提出在开展整流罩分离计算时，将每个因素都作为计算变量考虑；罩外动压、铰链摩擦力可通过理论公式进行计算；罩内负压和纵向分离面挡风板摩擦力可通过地面试验获取；根据罩内负压和罩外动压的分布特点，可将其工程简化为若干个集中力。这种将每个因素作为变量开展整流罩分离计算的方法，称为多因素计算方法。

根据角动量定理，整流罩分离动力学控制方程见公式（1）。

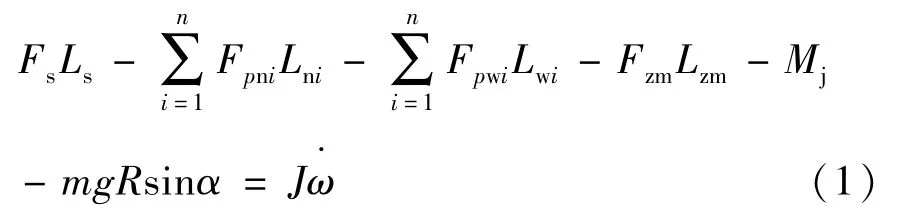
式中：

Fs—分离弹簧的推力合力，单位N；

Ls—分离弹簧的推力合力作用线与半罩转动中心的距离，单位m；

Fpni—罩内负压作用力，i=1、2、3……n，单位N；

Lni—罩内负压作用力作用线与半罩转动中心的距离，单位m；

Fpwi—罩外动压作用力，i=1、2、3……n，单位N；

Lwi—罩外动压作用力的作用线与半罩转动中心的距离，单位m；

Fzm—纵向挡风板摩擦力的合力，单位N；

Lzm—纵向挡风板摩擦力的合力作用线与半罩转动中心的距离，单位m；

Mj—铰链摩擦力矩，单位Nm；

m—瓣罩质量，单位kg；

g—重力加速度，单位9.8 m/s2；

R—瓣罩旋转半径，即瓣罩质心到转轴轴线的距离，单位m；

J—瓣罩对转轴的转动惯量，单位kg·m2；

ω—瓣罩转动角速度，单位rad/s；

ωd—瓣罩质心过顶角速度，单位rad/s；

α—瓣罩转角，定义为：瓣罩运动过程中，瓣罩质心C和转轴中心O的连线与OX轴的夹角；在整流罩初始装配状态下，α=α0，称α0为质心过顶角，如图1所示。

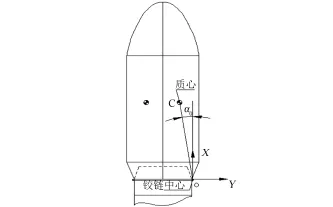
图1　整流罩分离初始状态图示Fig.1 Initial state of faring separation

罩内负压和罩外动压作用力计算时，可将整流罩沿轴向划分为若干个区域，每个区域的罩内负压作用力计算见公式（2），罩外动压作用力计算见公式（3）。

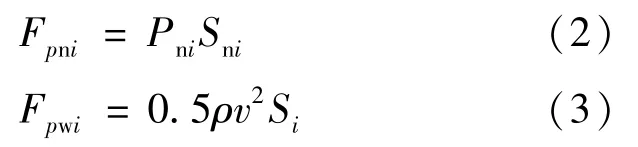
式中：

Pni—每个区域中心的负压，单位Pa，通过地面分离试验获取；

Sni—每个区域的负压作用有效面积，单位m2。

ρ—空气密度，取ρ=1.225 kg/m3；

v—每个区域中心的气流速度，即半罩每个区域中心点的运动速度，单位m/s；

Si—每个区域的压力作用有效面积，Si=Sni。

罩内负压需通过整流罩分离地面试验获取，试验时，要求整流罩结构真实、整流罩内的有效载荷包络真实，要求整流罩内负压测点的布置具有典型性和代表性。

纵向解锁装置挡风板处的摩擦力Fzm，可通过分离装置挡风板阻力试验获取。试验时，采用一定长度的纵向解锁装置，按准静态加载，测量挡风板处的摩擦力，然后再按线性关系计算Fzm。

铰链摩擦力矩Mj的计算见式（4）：

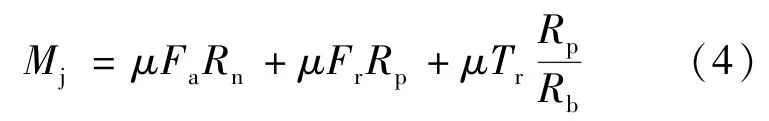
式中：

μ—摩擦系数；

Fa—铰链轴向支反力，单位N；

Rn—对应轴向支反力的摩擦力臂，单位m；

Fr—铰链径向支反力，单位N；

Rp—转轴半径，单位m；

Tr：铰链所受弯矩，单位Nm；

Rb—铰链所受弯矩作用力臂，即铰链支座宽度，单位m。

铰链摩擦力矩与铰链的受力及尺寸相关，计算与获取较简单。

2.2 飞行状态整流罩分离计算方法

运载火箭飞行过程中整流罩分离时接近真空环境，因此整流罩打开时罩内负压可忽略不计，分离运动时的罩外动压也可忽略不计。因此，作用于整流罩的外力有：分离弹簧推力、纵向分离面挡风板摩擦力和铰链摩擦力。根据角动量定理，飞行状态整流罩分离动力学控制方程见公式（5）。

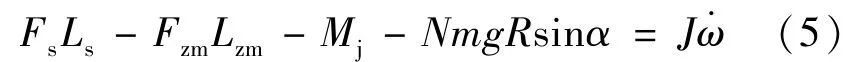
式中N为整流罩分离时刻火箭飞行过载系数。

2.3 整流罩分离传统计算方法

整流罩分离计算传统方法是将罩内负压、罩外动压、纵向分离面挡风板摩擦力和铰链摩擦力等因素折算为弹簧效能系数［3-4］（简称：效能系数计算方法），因此地面试验和飞行状态整流罩分离计算的动力学控制方程见公式（6），式中η为弹簧效能系数。

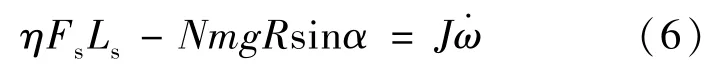
一般通过地面试验获取分离运动参数，使用过顶角速度等关键参数修正仿真计算模型，从而确定弹簧效能系数［3-4］。

3　罩内负压特性分析

由第2章分析可以看出，影响整流罩地面试验状态分离计算的诸多因素中，罩内负压参数的获取和使用的难度均较大。通过采用流固耦合算法可计算空气动力对整流罩分离运动的影响规律［1］，但计算时间较长，计算误差较大。本章通过地面分离试验，获取罩内负压参数，并且通过对罩内负压特性的分析，确定选取典型测点数据应用于整流罩分离计算。

3.1 分离试验方案概述

分离地面试验采用较为典型带有倒锥段的整流罩试件，整流罩沿纵向有一个分离面，分为两个半罩。试验在地面大气环境中开展，在整流罩试件内部安装有效载荷模拟件。

针对整流罩结构对称的特点，考虑到测点布置的可操作性，在模拟有效载荷上布置负压测点，测量整流罩打开过程中的负压数据，同时测量半罩的分离角速度等运动参数。负压测点共布置了30个，对应Ⅱ半罩的模拟有效载荷相应位置处布置了25个，见图2。对应Ⅳ半罩的模拟有效载荷相应位置处布置了5个，见图3。

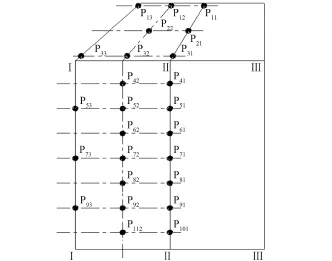
图2　整流罩Ⅱ半罩内负压测量布置Fig.2 Arrangement of negative pressure measurement point inside the half faringⅡ

3.2 负压测量结果分析

沿箭体轴线方向，整流罩内部负压曲线对比情况见图4～6，图中纵坐标数据均进行了归一化无量纲处理。可以看出有以下规律：

1）整流罩开始分离时刻，内部开始出现负压；0.5 s以后负压数值在零轴附近震荡收敛，近似为零。

2）由于整流罩为旋转分离，上部开始分开，故负压峰值随着高度的下降而减小，并且峰值出现时刻随着高度的下降而滞后。

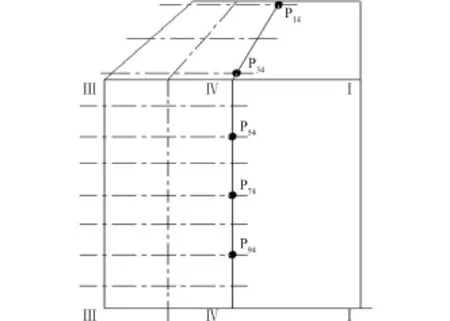
图3　整流罩Ⅳ半罩内负压测量布置Fig.3 Arrangement of negative pressure measurement point inside half faringⅣ

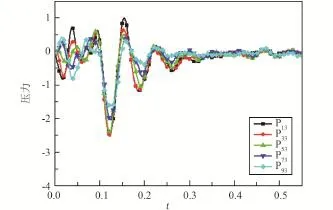
图4　Ⅰ基准线测点压力曲线Fig.4 The pressure curve of base lineⅠmeasurement points

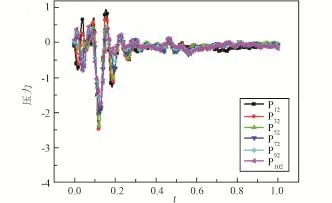
图5　Ⅰ偏Ⅱ基准线45°测点压力曲线Fig.5 Pressure curve of the measurement points which is 45°position between base lineⅠandⅡ

图6　Ⅱ基准线测点压力曲线Fig.6 The pressure curve of base lineⅡmeasurement points

选取整流罩的几个典型高度位置，对同一高度位置处环向的测量结果进行对比分析，各测点压力曲线对比情况见图7～10，图中坐标数据均进行了归一化无量纲处理。可以看出，在同一个高度位置处，压力曲线基本一致。

图7　第1排高度测点曲线Fig.7 The pressure curve of the first row measurement points

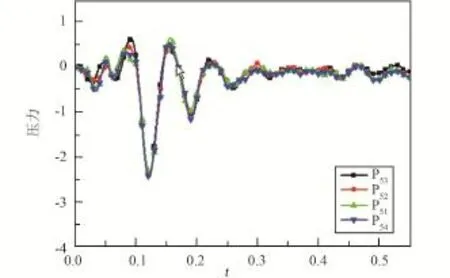
图8　第5排高度测点曲线Fig.8 The pressure curve of the fifth row measurement points

通过对罩内压力分布特点的分析可知，进行分离计算时，需选取不同高度位置处的数据，将整流罩沿纵向分为几个典型的区域；同一高度位置处可以仅选用一个测点的数据进行简化；负压曲线仅采用0～0.5 s之间的测量数据，0.5 s之后的数据可忽略不计。

通过针对罩内负压测量曲线的数值比较，可以看出P21、P11和P31的算术平均值近似相等；分离计算时选取P21代表前锥区域的内压特性；同理，选取P51代表柱段前部的内压特性；选取P91代替柱段后部的内压特性。由于测点布置空间等因素的影响，未在倒锥段区域布置测点，选取P101近似代表倒锥区域的内压特性。

图9　第7排高度测点曲线Fig.9 The pressure curve of the seventh row measurement points

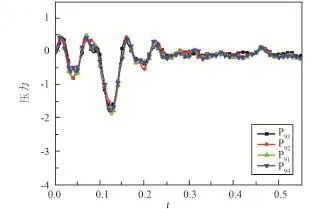
图10　第9排高度测点曲线Fig.10 The pressure curve of the ninth row measurement points

4　整流罩地面分离试验仿真计算

4.1 气动作用力计算方法

4.1.1 罩内负压作用力

通过对罩内负压特性的分析，在分离仿真计算时，可使用Ⅱ基准线测点的压力，将整流罩沿高度方向上划分为四个区域，选用P21（前锥区域）、P51（柱段前部）、P91（柱段后部）和P101（倒锥区域）等共计4个典型测点的压力。每个区域的罩内负压作用力按公式（2）计算。

4.1.2 罩外动压作用力

计算罩外动压作用力时，将罩子划分为四个区域，与计算罩内负压作用力时的四个区域相同。每个区域的罩外动压作用力按公式（3）计算。

4.2 仿真计算与试验结果对比分析

选取某半罩作为计算对象，采用多因素计算方法；对半罩施加罩内负压、罩外动压、摩擦力、分离弹簧力和重力。采用效能系数计算方法时，为了使过顶角速度与试验值接近，取效能系数η=0.5。

整流罩分离角速度随时间变化历程计算结果与试验结果对比情况见图11，图中纵坐标数据进行了归一化无量纲处理。整流罩分离运动主要参数测量值与计算值对比情况见表1。

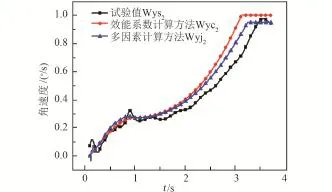
图11　半罩角速度曲线对比Fig.11 The contrast of the half faring angular velocity curve

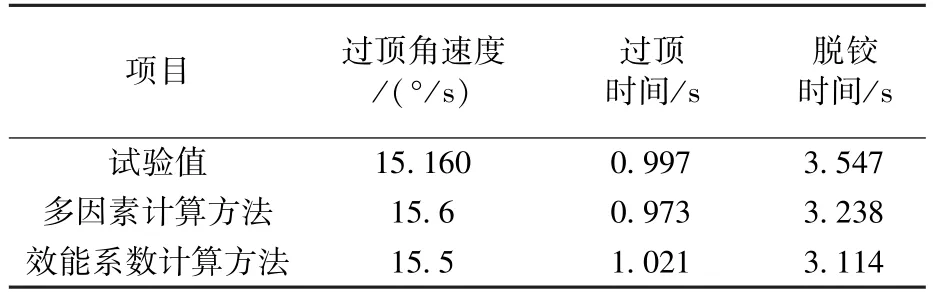
表1　仿真计算与试验结果对比Table 1 Comparison between simulation and test results

从对比情况可以看出：

1）采用多因素计算方法计算出的角速度曲线与试验测量曲线一致性较好；

2）采用效能系数计算方法时，除了过顶角速度一致性较好，其它参数一致性较差，而且随着分离时间的增大，角速度曲线与测量曲线的偏差越大。

采用效能系数计算方法有以下不足之处：

1）根据分离试验结果及过顶角速度指标，通过选取效能系数修正理论计算模型，计算出的分离角速度曲线与实测值偏差较大，尤其是脱胶角速度等指标。

2）通过地面试验修正理论模型时，摩擦力、罩内负压和罩外气动作用力均通过效能系数进行折算；但是，对于飞行状态，由于没有罩内负压和罩外气动作用力的影响，因此效能系数方法不能对飞行状态整流罩分离进行准确计算。

5　飞行状态整流罩分离仿真计算

一般情况下，运载火箭飞行至真空环境时，整流罩开始分离，这时当地大气压近似为零，由于整流罩排气孔的排气作用，罩内压力也近似为零；因此，计算飞行状态整流罩分离时，除了取消罩内负压作用力和罩外气动作用力以及过载系数不同外，其余参数同地面试验状态。使用经过地面试验验证过的分离计算模型，采用多因素计算方法和效能系数计算方法分别开展了整流罩分离计算。两种计算方法得出的整流罩分离角速度对比情况见图12，图中纵坐标数据进行了归一化无量纲处理。两种计算方法获取的主要参数计算值对比情况见表2。

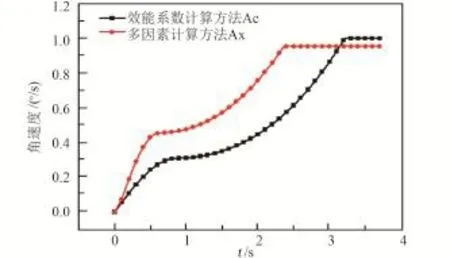
图12　分离角速度曲线对比Fig.12 Contrast of the angular velocity curve

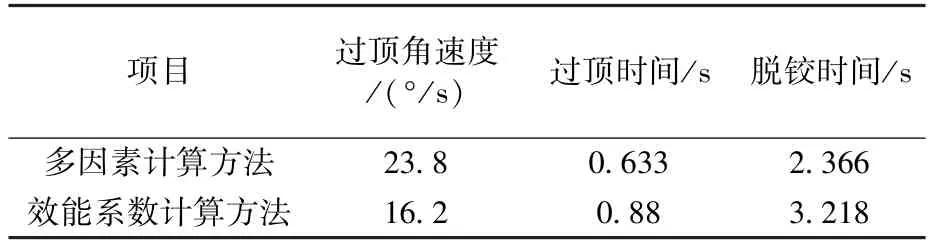
表2　两种计算方法的计算结果对比Table 2 Comparison of calculation results between the two methods

从对比曲线可以看出，根据效能系数计算方法得出的计算结果比多因素计算方法的数值偏小很多。这是因为效能系数计算方法使用的效能系数是地面试验修正得出的，包含了罩内负压及罩外气动压力的影响等因素，然而飞行状态时不需考虑这两个因素的影响；这是效能系数计算方法的固有缺陷。此缺陷导致针对飞行状态的预示结果偏差过大，不利于整流罩分离系统设计及分离方案评估。

6　结论

多因素计算方法可直接应用于飞行状态整流罩分离计算，不需通过整流罩分离地面试验修正计算模型，可降低研制成本，节省研制周期；然而效能系数方法必须通过地面分离试验修正效能系数，应用于飞行状态整流罩分离计算时，无法剔除气动影响，计算误差较大。

相对于效能系数方法，多因素计算方法能够明确的表征整流罩分离运动的各影响因素，对飞行状态整流罩分离进行更加准确的预示和评估；开展各影响因素的灵敏度分析，找出影响整流罩分离的关键要素，更加有效地指导分离系统方案设计，具有更加显著的工程应用价值。

多因素计算方法通过了整流罩地面分离试验的验证，后续可通过测量飞行状态整流罩分离运动参数对该方法开展进一步验证。

（References）

［1］张大利.火箭整流罩分离过程仿真分析［D］.哈尔滨：哈尔滨工业大学，2013.Zhang Dali.The Lauch Vhecle's Faring Separation Simulation Analysis［D］.Harbin：Harbin Institute of Technology，2013.（in Chinese）

［2］马忠辉.大型弹性整流罩分离特点分析［J］.中国科学：E辑，2009（3）：482-489.Ma Zhonghui.The Separation Characteristic Analysis of Large Scale Faring［J］.Chinese Science：E，Volume，2009（3）：482-489.（in Chinese）

［3］李长纯.长征二号E有效载荷整流罩分离技术［J］.中国航天，1992（9）：11-15.Li Changchun.The Separation Technology of Payload Faring of Long March 2-E［J］.China Aerospace，1992（9）：11-15.（in Chinese）

［4］龙乐豪.导弹与航天丛书—总体设计［M］.北京：宇航出版社，1989：523-531.Long Lehao.Missile and Spaceflight Series-Integrated Design［M］.Beijing：Aerospace Publishing House.1989.（in Chinese）

［5］刘建，李海阳.基于ADAMS的整流罩分离仿真技术研究［J］.载人航天，2008，14（1）：26-28.Liu Jian，Li Haiyang.The Separation Simulation Technology Research of Payload Faring Based on ADAMS［J］.Manned Spacefight，2008，14（1）：26-28.（in Chinese）

Research on Method of Faring Separation Calculation

GU Mingkun1，ZHANG Lu1，WU Jie1，HE Yuanjun2，LIU Lidong1
（1.Beijing Institute of Aerospace Systems Engineering，Beijing 100076，China；2.China Manned Space Agency，Beijing 100720，China）

The traditional energy coefficient calculation method cannot forecast the faring separation accurately.Taken the typical rotation casting faring as the example，a new multi-factor calculation method was proposed which set every factor as the variable.The faring separation dynamic equation was established and the method to compute each factor was discussed.Then the ground separation test was carried out with a real rotation casting faring.The negative pressure characteristics and the separation motion parameters were obtained which demonstrated that the calculation result was consistent with the test result.Comparing with the traditional energy coefficient calculation method，the multi-factor calculation method is more accurate and more efficient to guide the faring separation system scheme design.It which has prominent engineering application value.

fairing separation；multi-factor；negative pressure；frictional force

V19

A

1674-5825（2016）05-0602-06

2016-04-15；

2016-07-28

总装备部运载专业组“十二五”预研创新课题基金（51320120102）

顾名坤（1983-），男，硕士，工程师，研究方向为飞行器总体设计。E-mail：18510695979@163.com