改进的TOPSIS模型在陕西省农业干旱脆弱性区划中的应用
徐 晗
(1.长安大学环境科学与工程学院, 陕西 西安 710054; 2.陕西学前师范学院环境与资源管理系, 陕西 西安 710100)
改进的TOPSIS模型在陕西省农业干旱脆弱性区划中的应用
徐晗1,2
(1.长安大学环境科学与工程学院, 陕西 西安 710054; 2.陕西学前师范学院环境与资源管理系, 陕西 西安 710100)
以陕西10个地市作为研究对象,从暴露性、敏感性以及恢复能力三个方面选取12个指标构建农业干旱脆弱性评价指标体系,应用改进的TOPSIS模型计算得出各市区的相对贴近度,对陕西省农业干旱脆弱性进行综合评价。结果表明:陕西省农业干旱脆弱性存在地域性差异,10个市区的农业干旱脆弱性由高到低排序依次为安康(0.7841)>商洛(0.7650)>汉中(0.6939)>西安(0.5977)>榆林(0.4657)>延安(0.4605)>渭南(0.4555)>铜川(0.4319)>宝鸡(0.3525)>咸阳(0.2996),整体呈现“南高北低”的分布格局;从暴露性来看,陕西省农业干旱暴露性指数最高为渭南,其次为咸阳和西安,其它市区均较低;从敏感性来看,陕西省农业干旱敏感性分布两极分化严重,主要表现为陕南地区敏感性总体偏高,关中地区和陕北地区除铜川市和延安市敏感性较高外,均处于较低水平;从恢复能力来看,陕西省农业干旱的恢复力分布无明显规律,按其恢复力由高到底排序依次为:延安>渭南>榆林>咸阳>西安>铜川>宝鸡>汉中>安康>商洛。改进的TOPSIS模型能较合理地从整体上对农业干旱脆弱性进行评价分区,符合实际情况,为其他多属性综合评价提供了一个新的思路和算法。
农业干旱脆弱性;评价;改进TOPSIS模型;KL距离;熵权法;陕西省
随着人口增加和经济发展,旱灾所造成的损失也越来越严重[1]。近年来全球气候变暖加快,引起农业自然灾害频发,干旱不仅直接导致农业减产、食物短缺、病虫害高发、作物生产力降低等,其持续累积还会引起土地资源退化、水资源耗竭和生态环境破坏,从而制约农业的可持续发展[2-3]。
农业干旱脆弱性是指农业生产系统易于遭受干旱威胁与损失的性质和状态,反映了整个农业系统对干旱的适应、反应和应对能力。它主要受两类因素影响:一类是加剧农业干旱危害的各种因素的总和,从负面影响农业干旱脆弱性;另一类是减轻农业旱灾危害的各种有利因素总和,从正面影响农业干旱脆弱性[2]。干旱脆弱性越强说明发生旱灾的风险越高,灾情可能越严重。因此,进行农业气候干旱脆弱性评价和预警对预防与抗减旱灾有重要意义。
目前,国内外对于农业干旱脆弱性评价的研究才刚起步,评估方法还很不成熟。国内外学者对于干旱脆弱性评估方法的研究主要集中在评估指标的选取、指标因子权重的确定以及脆弱性评价方法的选择,如倪深海等选取水资源承载能力子系统、抗旱能力子系统、农业旱灾子系统三个方面的评价指标,构造层次分析模型绘制了中国农业干旱脆弱性分区图[4],曹永强等利用投影寻踪技术对大连市农业干旱脆弱性进行分区评价[1];陈萍等从暴露度、敏感性和适应能力三个方面给出鄱阳湖生态经济区农业干旱脆弱性指数(DVI),并对其干旱脆弱性进行等级划分[5],王莺等利用主成分分析法对中国南方地区干旱脆弱性进行评价[6];程静从经济脆弱性、社会脆弱性、政治脆弱性三个方面选取指标,利用层次分析法(AHP)和模糊综合评价法对湖北省孝感市的农业干旱脆弱性进行评价并对影响因素进行识别[7]。此外,密切值法[8]、TOPSIS法、集对分析法[9]等也都被尝试应用于农业干旱脆弱性评价中,但由于这些方法的使用都不成熟,因此有很多地方需要探索和改进以得到更加科学合理的评价结果。
TOPSIS方法作为经典的多属性决策方法之一,首先被Hwang和Yoon用来研究多属性决策问题。目前,已被广泛地应用于水资源评价、土地资源评价、脆弱性评价等领域中来解决混合型多目标(属性)决策问题[10]。
TOPSIS方法基本原理是首先根据评价指标的标准化值与其权重构成的规范化矩阵确定评价指标的正、负理想解,然后计算评价指标与正、负理想解之间的理想距离,最后对评价方案与最优理想参照点之间的距离进行模糊评判[11]。但传统的TOPSIS法存在一定的局限性,首先确定权重时存在主观化问题,用欧氏距离判断方案贴近理想解程度时,出现离正理想解和负理想解距离相等的问题[11-12],并且该方法目前较少应用于农业干旱脆弱性评价中,因此首次尝试利用改进的TOPSIS模型对市域内的农业干旱脆弱性评价进行研究,以提高评价结果的科学性和适应能力。
1 研究区概况与数据来源
1.1研究区概况
陕西省位于我国西北内陆中部,地理坐标为东经105°29′~111°15′,北纬31°42′~39°35′,总面积20.56×104km2,辖西安、铜川、宝鸡、咸阳、渭南、榆林、延安、汉中、安康、商洛10个地市。2013年总人口3 764万人,其中农业人口1 833万人,非农业人口1 931万人。全省地势南北高,中间低,西部高,东部低,构成境内地形地貌繁杂多样,全省地貌为北部陕北黄土高原,中部为关中盆地,南部为秦巴山地。陕西地处内陆,属典型的大陆性气候,降水量分布不均,主要集中在6—9月,全省多年平均降水量为666.9 mm。冬季干冷,夏季湿热,季风气候特点明显。温度1月最低,7月最高,春季陡升,秋季快降,春季温度(4月)略高于秋季温度(10月)[13]。全省耕地主要分布于陕北北部的沙漠草原、黄土台塬、关中盆地及陕南秦巴山区的山间盆地,总面积398.5万hm2。
干旱为陕西省主要的农业气象灾害,根据历史资料统计分析,近几十年陕西农业受旱面积呈增加趋势,农业旱灾发生的季节性和区域性特征明显,陕西以夏旱居多,占各类季节性干旱频次的31.25%,陕北以夏旱和春旱居多,主要干旱时段集中在3—6月,关中夏旱和冬春连旱居多,主要时段集中在6—8月,陕南夏伏旱占多数,其中关中发生干旱频次最多[14]。
1.2数据来源
本文中各地市的指标数据来源于《陕西省统计年鉴》[15]、《陕西水利统计年鉴》[16]及各地市的统计数据,其中降雨量、温度等数据采用1994—2013年陕西省各气象站点监测的气象数据。
1.3农业干旱脆弱性评价指标体系
农业干旱脆弱性评估,一般先需确定脆弱性分析的基本内容和评价指标,然后对各指标进行赋权。考虑到陕西省农业干旱的形成主要受自然因素和社会经济因素共同作用,在科学性、完整性和数据可获取的前提下,从暴露度、敏感性和适应能力三个方面选取12个指标对陕西省10个地市构建陕西省农业干旱脆弱性评价指标体系。
农业干旱脆弱性评价中暴露性是指造成干旱灾害的自然、社会等变异因素及其程度,这些变异因素主要是指极端的气候条件(如无雨或少雨、空气干燥和干热、蒸发量大等)、水文条件、自然地理环境、人口情况等;一般地,暴露性越大,发生农业干旱的风险越大。
农业干旱敏感性,是指研究区域内可能受到干旱缺水威胁的对象由于潜在的干旱危险因素而造成的伤害或损失程度。一般地,敏感性越高,在相同受旱条件下的干旱灾害损失越大,干旱灾害风险也越大,反之亦然。
农业干旱恢复能力是指在研究区域内,预防和减轻干旱灾害风险的能力以及灾后的恢复程度和速度,主要包括社会经济发展水平、水利工程建设水平和科技生产等方面。恢复能力越强,可能遭受的潜在损失就越小,干旱灾害风险则越小。

表1 陕西省农业干旱脆弱性评价指标体系
2 TOPSIS法的改进
2.1TOPSIS模型传统算法存在的问题评述
TOPSIS模型是根据备选方案集的指标性质和数据,以一组最优指标数据作为虚拟正理想方案,以一组最劣指标数据作为虚拟负理想方案,通过比较方案点距正、负理想点的欧氏距离大小来判断被评价方案的优劣[12],若最接近正理想解,同时又最远离负理想解,则该方案是备选方案中最好的方案[17]。
但传统的TOPSIS法中存在两个问题:一是在确定各评价指标权重时主要采用Delphi法、AHP法等主观赋权方法,其权重结果受主观因素影响大,存在一定程度的不合理性;二是以欧氏距离为基础来判断方案贴近理想解的程度,在实际操作中可能出现与理想解距离近的方案与负理想解的距离也近的情况,这样就不能完全科学地反映各方案的优劣。
2.2TOPSIS模型算法的改进
针对上述两点不足,对TOPSIS模型进行改进。一是采用熵权法确定指标权重;二是利用相对熵,即Kullback Leibler(KL)距离替代欧式距离计算与理想方案的贴进度,最终得出方案的优劣排序。
2.2.1建立农业干旱脆弱性评价的初始决策矩阵假设每年有m个城市,n个评价指标,则根据指标统计值可建立如下初始决策矩阵,其中Zij为第i个城市Mi的第j个指标值。
(1)
2.2.2初始决策矩阵的标准化由于初始数据具有不同的量纲和数量级,为使其具有可比性,需要对初始决策矩阵进行标准化。该标准化过程按照式(2)进行。
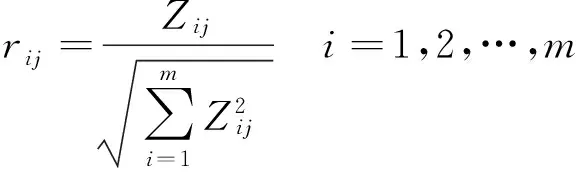
(2)
式(1)经过标准化处理以后,得到标准化矩阵R=rij(m×n),其中rij是第i个城市第j个指标的标准化值。
2.2.3构建规范化决策矩阵将rij和各评价指标权重Wj=(W1,W2,…,Wn)相乘得到加权标准化矩阵,即规范化决策矩阵X=(Xij)m×n,其中
Xij=wj×rij,i=1,2,…,m,j=1,2,…,n
(3)
在这里,各指标的权重wj采用熵权法(28)进行计算,由于该方法已经比较成熟,在此将不再赘述。
2.2.4确定正理想解X+和负理想解X-

(4)

(5)


赵萌、邱菀华等在“基于相对熵的多属性决策排序方法”中提出了一种新的计算与理想解贴近度的方法——相对熵,即KL距离。研究结果表明, 在传统的TOPSIS方法、夹角度量法和投影算法排序都失效的情况下, 相对熵排序法能够准确地给出方案的排序[11-12]。KL距离值计算公式如下:
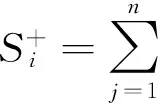
(6)

(7)
2.2.6计算评价对象与理想解之间的贴近度Ci
各城市评价指标到正理想解的相对距离称为相对贴近度,用下式计算:
(8)
Ci越大,表示越接近正理想解,表明该地市农业干旱脆弱越高。当Ci值为1时,说明该区县的农业干旱脆弱性刚好为正理想解;当Ci值为0时,说明该地市的农业干旱脆弱性刚好为负理想解。因此Ci值是介于0和1之间的,根据贴近度的高低,可将陕西省的农业干旱脆弱性划分为高、较高、中、低4个等级。
3 结果与分析
3.1标准化决策矩阵的建立
利用式(1)、式(2)进行标准化处理后的矩阵Rij如下:

3.2确定评价指标权重及正负理想解
根据熵权法计算得出指标权重,根据式(3)构建规范化决策矩阵,式(4)、(5)确定各指标的正、负理想解,详见表2。
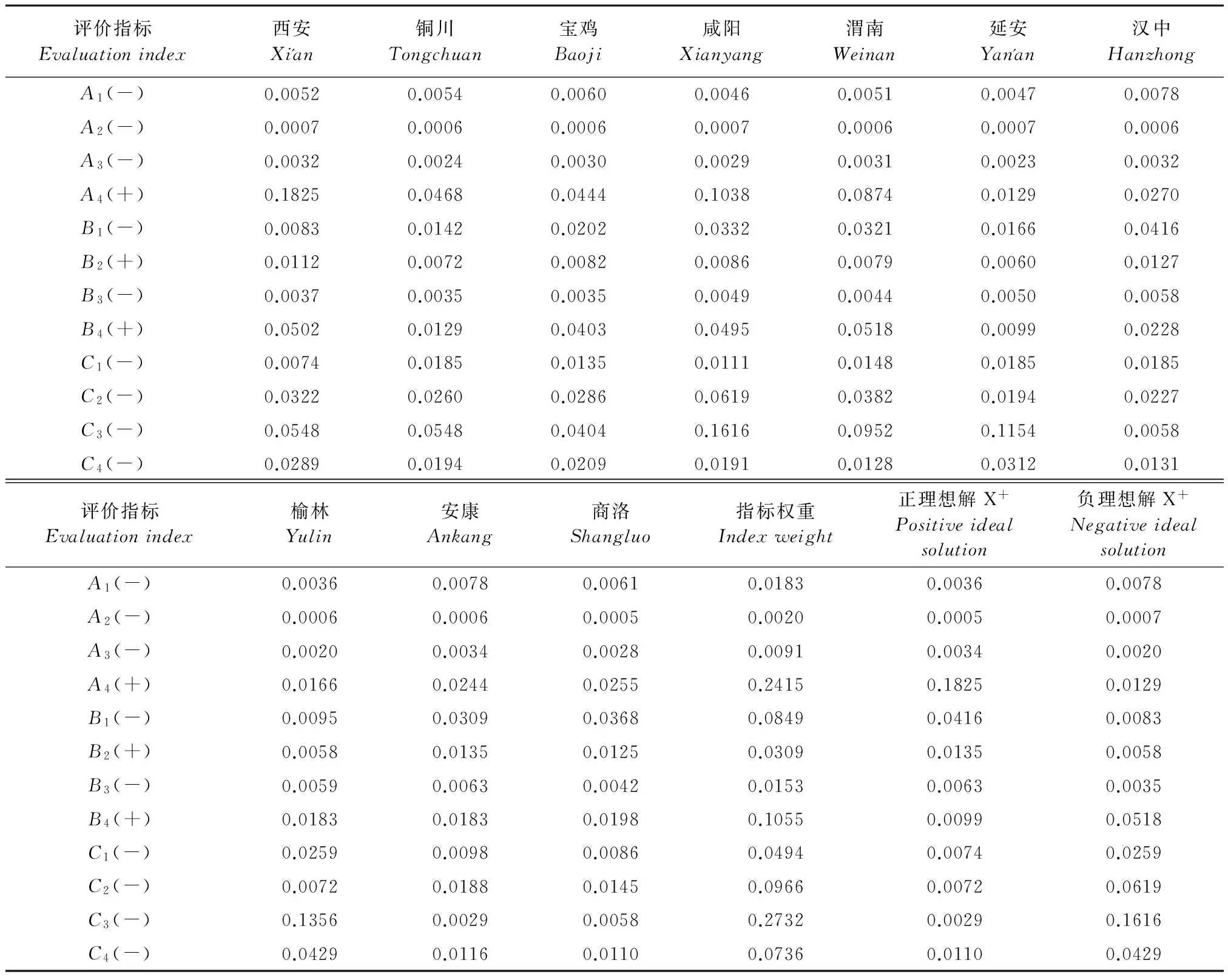
表2 陕西省评价指标权重、规范化决策矩阵与正、负理想解
3.3确定指标的正、负理想距离与评价对象的贴近度
根据式(6)、式(7),利用KL距离计算陕西省各地市评价指标距正、负理想解的距离,然后根据式(8)计算各评价对象的相对贴近度,计算结果见表3。

表3 各评价指标的正、负理想距离及相对贴近度
3.4评价结果分析
3.4.1农业干旱脆弱性分析与区划利用改进的TOPSIS模型计算得出陕西省10个地市的农业干旱脆弱性及各评价子系统的指标指数(表3)。此外,运用标准差分级法[18],利用贴近度Ci的平均值(V=0.5306)和标准差(B=0.1670),将陕西省划分为低脆弱区、中脆弱区、较高脆弱区和高脆弱区(表4),并运用ARCGIS10.0绘制西安市农业干旱脆弱性区划图(图1),以直观显示农业干旱脆弱性的空间分异。

表4 陕西省农业干旱脆弱性分级

图1陕西省农业干旱脆弱性空间分布
Fig.1ThespatialdistributionmapofagriculturaldroughtvulnerabilityinShaanxiProvince
从图1和表3中可以看出,陕西省农业干旱脆弱性呈现“南高北低”的分布格局,各地区农业干旱脆弱性的贴近度按从大到小的顺序依次为:安康(0.7841)>商洛(0.7650)>汉中(0.6939)>西安(0.5977)>榆林(0.4657)>延安(0.4605)>渭南(0.4555)>铜川(0.4319)>宝鸡(0.3525)>咸阳(0.2996)。其中商洛和安康处于高脆弱区,汉中和西安处于较高脆弱区,榆林、延安、铜川和渭南处于中脆弱区,宝鸡和咸阳处于低脆弱区,总体来看,关中地区除西安市以外总体农业干旱脆弱性较低,其次为陕北地区,而陕南低区农业干旱脆弱性最高,由此可看出农业干旱脆弱性的分布与气候干旱分布不完全一致。
从该结果可以看出,陕南地区虽然降水量最高,地表水资源丰富,只能说明其暴露性指数较低,但是农业干旱脆弱性并不仅仅与水量是否丰富有关,它是农业生产系统易于遭受干旱威胁与损失的性质和状态,反映了整个农业系统对干旱的适应、反应和应对能力,首先陕南地区3个城市的农业产值比例和农业人口比重都很高,说明其对农业干旱的敏感性很高,一旦发生农业干旱,对其造成的影响会很大;另外其水田面积比重以及复种指数都偏高,说明其作物的需水量非常大,相比干旱的陕北地区所耕种的旱作植物,对干旱会更为敏感;其次陕南地区三个城市虽然地表径流量大,但是水库调蓄率都很低,说明其对地表水的有效开发利用程度很低;另外其耕地灌溉率也很低,说明其水利设施建设程度较差,不能够在少雨的季节保证作物的灌溉;最后,3个城市的人均GDP都很低,说明其经济发展水平相对关中和陕北地区落后,其对干旱的恢复能力较差。综上所述,陕南地区虽然暴露度低,但是由于其对干旱的敏感性较高以及对干旱的恢复能力较差,导致其农业干旱脆弱性在全省范围内处于较高的状态,是有其科学性和合理性的。
3.4.2暴露性分析由表3和图2可知,陕西省农业干旱暴露性指数除西安、咸阳和渭南较高外,其它市区均较低,其中最高为渭南(0.9221),其次为咸阳(0.9210)和西安(0.8371),分析3个城市暴露性高的原因主要为:与关中地区的另外两个城市相比,这3个城市的人口密度均偏高,尤其是西安高达846 人·km-2,咸阳和渭南也分别有481 人·km-2和405 人·km-2,使得这两个城市人口作用于土地和水资源的压力过大,另外咸阳市的降水量相对较低,年均降水量仅为497.98mm,西安和渭南的年均温度较高,分别为14.9℃和14.4℃,同时渭南地区的土壤保水保肥能力相对较差,也是其暴露性高的原因之一。陕北地区的榆林和延安,其降雨量很小,但同时其人口密度非常低,年均气温也很低,因此其暴露性较低,而陕南地区的商洛、安康和汉中,其暴露性低的原因主要为降水量很大和人口密度较低。
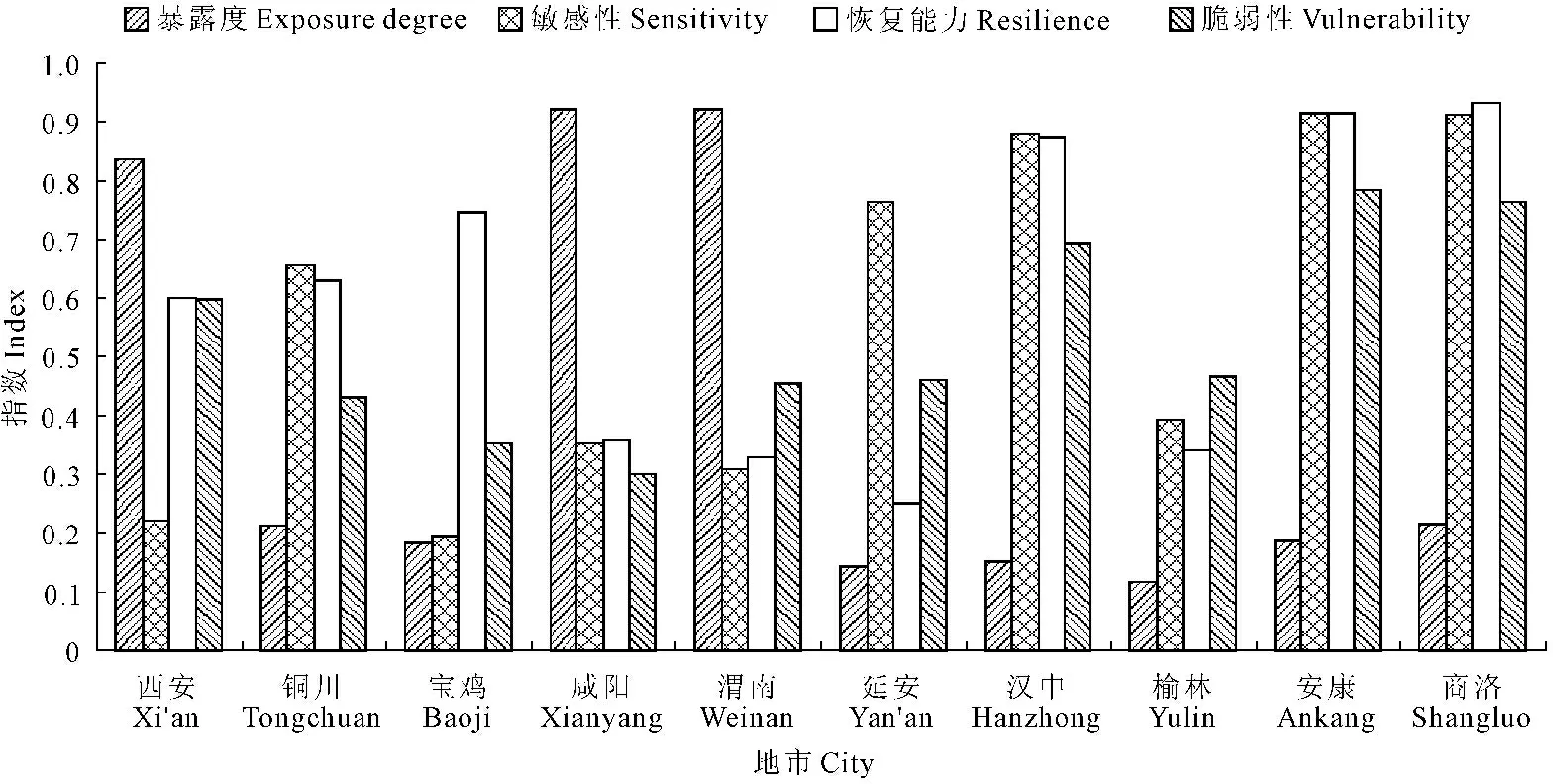
图2陕西省农业干旱脆弱性以及暴露性、敏感性、恢复能力对比分析
Fig.2Thecomparativeanalysisofagriculturaldroughtvulnerability,exposuredegree,sensitivityandresilienceinShaanxiProvince
3.4.3敏感性分析由表3和图2可知,陕西省农业干旱敏感性分布两极分化严重,主要表现为陕南地区敏感性总体偏高,其中安康高达0.9167,商洛和汉中分别为0.9114和0.8810,关中地区和陕北地区除铜川(0.6561)和延安(0.7632)敏感性较高外,均处于较低水平,分析出现该结果的原因主要为:陕南地区的3个城市农业产值比和复种指数均较高,其中农业产值比最高为汉中,高达35%,安康和商洛分别为26%和31%,说明3个城市对农业生产的依赖性均较高,另外复种指数最高为安康(2.29),其次为汉中(2.16)和商洛(2.13),说明3个城市耕地利用率较高,作物需水量较大;同时3个城市的耕地灌溉率均处于较低水平,最高的汉中也只有30%,说明其水利设施水平也较低;另外汉中和安康的农业人口比重过高,分别为77%和84%,说明当地人口对于农业的依赖性较高。而铜川和延安都是由于耕地灌溉率过低导致敏感性偏高,分别为17%和13%。
3.4.4恢复力分析由于恢复力指数为负向指标,即恢复力越强,干旱脆弱性越低,因此,由表3和图2可知,陕西省农业干旱的恢复力分布无明显规律,按其恢复力由高到低排序依次为:延安>渭南>榆林>咸阳>西安>铜川>宝鸡>汉中>安康>商洛。分析出现该结果的原因为:恢复力排名前三的城市中,4个恢复力指标均有3个处于较高水平,延安市人均耕地面积为0.15hm2、水库调蓄率40%、人均GDP61 493元,在全省范围来看都位于前列;渭南市的人均耕地面积0.12hm2,水库调蓄率35%,单位面积农用化肥量1.16t;榆林市人均GDP高达84 634元,为全省最高,人均耕地面积0.21hm2,水库调蓄率45%,说明3个城市的人口作用于土地的压力较小,地表水开发利用水平均较高,同时灾后重建能力较强。恢复力排名后三位的均为陕南地区的3个城市,其重要原因为这3个城市恢复力指标中最差的表现为人均GDP均处于全省较低水平,最高的汉中也只有25 769元,因此其灾后重建能力很差,另外水库调蓄率极极低,均只有1%或2%,说明虽然地表径流量大,但是其开发利用水平不高。
4 结 论
本次研究采用的基于熵权和KL距离的改进TOPSIS模型,不仅避免了赋权的主观因素干扰,而且有效避免了指标距正理想解与负理想解的距离都近的情况,提高了模型的精度,从而大大提高了计算结果的科学性和合理性。经过本文研究论证表明,利用改进的TOPSIS模型计算得出的相对贴近度能较为直观和科学地比较出各区县之间农业干旱脆弱性的大小,符合陕西省的实际情况,说明该方法具有可行性,可为陕西省政府部门应对农业干旱提供一定管理依据,同时为其他多属性综合评价提供了一个新的思路和算法。
[1]曹永强,马静,李香云,等.投影寻踪技术在大连市农业干旱脆弱性评价中的应用[J].资源科学,2011,33(6):1106-1110.
[2]胡颖颖,玉米提·哈力克,塔依尔江·艾山,等.新疆2001—2010年农业气候干旱脆弱性分析[J].中国沙漠,2014,1(34):254-258.
[3]KimDaeHa,YooChulsang,KimTae-Woong.ApplicationofspatialEOFandmultivariatetimeseriesmodelforevaluatingagriculturaldroughtvulnerabilityinKorea[J].AdvancesinWaterResources, 2011,34:340-350.
[4]倪深海,顾颖,王会容.中国农业干旱脆弱性分区研究[J].水科学进展,2006,16(5):705-709.
[5]陈萍,陈晓玲.鄱阳湖生态经济区农业系统的干旱脆弱性评价[J].农业工程学报,2011,27(8):8-13.
[6]王莺,王静,姚玉璧,等.基于主成分分析的中国南方干旱脆弱性评价[J].生态环境学报,2014,23(12):1897-1904.
[7]程静.农业旱灾脆弱性及其风险管理研究[D].武汉:华中农业大学,2011.
[8]杨奇勇,李景保,蔡松柏.湖南农业干旱脆弱性分区研究[J].水资源与水工程学报,2007,18(3):46-49.
[9]李艳.河南省干旱承险脆弱性综合评价研究[D].郑州:郑州大学,2011.
[10]文洁,刘学录.基于改进TOPSIS方法的甘肃省土地利用结构合理性评价[J].干旱地区农业研究,2009,27(4):234-239
[11]任力锋,王一任,张彦琼,等.TOPSIS法的改进与比较研究[J].中国卫生统计,2008,25(1):64-66.
[12]李晓峰,刘宗鑫,彭清娥.TOPSIS模型的改进算法及其在河流健康评价中的应用[J].四川大学学报(工程科学版),2011,43(2):14-21.
[13]BekeleShiferaw,KindieTesfaye,MenaleKassie.Managingvulnerabilitytodroughtandenhancinglivelihoodresilienceinsub-SaharanAfrica:Technological,institutionalandpolicyoptions[J].WeatherandClimateExtremes, 2014,3:67-79.
[14]鲁春阳,等.基于改进TOPSIS法的城市土地利用绩效评价及障碍因子诊断——以重庆市为例[J].资源科学,2011,33(3):535-541.
[15]陕西省统计局.陕西省统计年鉴[M].北京:中国统计出版社,2014.
[16]陕西省水利厅.陕西省水利统计年鉴[M].西安:三秦出版社,2014.
[17]韦俊敏,胡宝清.基于改进TOPSIS法的土地整治合理度评价[J].资源科学,2013,35(7):1407-1414.
[18]赵萌,邱菀华,刘北上.基于相对熵的多属性决策排序方法[J].控制与决策,2010,25(7):1098-1100.
Application of improved TOPSIS model to agricultural drought vulnerability in Shaanxi Province
XU Han1,2
(1.CollageofEnvironmentalScienceandEngineering,Chang'anUniversity,Xi'an,Shaanxi710054;2.ShaanxiXueQianNormalUniversity,Xi’an,Shaanxi710100,China)
Taking 10 regions of Shaanxi Province as the study objects, and selecting 12 indexes including exposure, sensitivity and resilience, we established the index evaluation system of agricultural drought vulnerability. In addition, the relative similarity degree of different regions was calculated using the improved TOPSIS model. Based on the calculation results, we obtained the comprehensive evaluation of agricultural drought vulnerability in Shaanxi. The results showed that: Agricultural drought vulnerability in Shaanxi existed regional disparity. The agricultural drought vulnerability according to the order from high to low in the 10 regions were: Ankang (0.7841)>Shangluo (0.7650)>Hanzhong (0.6939)>Xi'an (0.5977)>Yulin (0.4657)>Yan'an (0.4605)>Weinan (0.4555)>Tongchuan (0.4319)>Baoji (0.3525)>Xianxang (0.2996), and the agricultural drought vulnerability in the southern part were higher than the north part. From the view of exposure, the highest index in Shaanxi was WeiNan, followed by Xianyang and Xi'an, being lower in other regions. On the basis of sensitivity, the polarization was serious, which was mainly manifested that the sensitivity was high in southern Shaanxi Province, and low in northern Shaanxi Province and Guanzhong area except Tongchuan and Yan'an. According to resilience, the distribution of agricultural drought in Shaanxi had no obvious regularity, showing an order of: Yan'an>Weinan>Yulin>Xianyang>Xi'an>Tongchuan>Baoji>Hanzhong>Ankang>Shangluo. Finally, it is concluded that the improved TOPSIS modle could generally evaluate the agricultural drought vulnerability reasonablely, agreeing with the actual situation and thus providing a new method for other multi-attribute evaluation.
agricultural drought vulnerability; evaluation; improved TOPSIS Model; KL distance; entropy weight method; Shaanxi Province
1000-7601(2016)04-0251-08
10.7606/j.issn.1000-7601.2016.04.38
2015-10-20
水利部公益性行业科研专项“渭河中下游干旱预警与应急水源配置(201301084);国家自然科学基金(41301618);陕西学前师范学院自然科学基金项目(2016JDKJ009)

S181;X171
A

