包装袋M边成型过程曲面研究
邓援超, 刘 放
(湖北工业大学机械工程学院, 湖北 武汉 430068)
包装袋M边成型过程曲面研究
邓援超, 刘放
(湖北工业大学机械工程学院, 湖北 武汉 430068)
分析塑编袋M边成形过程中的曲线和曲面,建立塑编袋在成型过程中的空间曲线及空间曲面的数学模型。对包装袋连续式成形过程进行分析,并得出成型渐变角的变化规律,从而为M边成型器的生产制造提供必要的数学依据。
M边成型器;M边曲面;渐变角;数学模型
内置式插边成型器广泛应用于食品、日化、医药、农副产品等包装袋,它是实现带M边的包装袋成型的重要器件。成型器的传统制造方法是根据袋子的宽度和折入深度以及一些经验制造出来,没有统一的理论为基础。本文通过建立内置式成型器的三维数学模型,并将其应用到数字化制造中,给出塑编袋连续式渐变成型数学模型的计算公式。
1 包装袋M边成型器的基本原理
包装袋插边成型器如图1所示。从图中可见,筒状包装袋经过内置式导向杆由AB边引至成型器CD边,沿内置式支撑板表面往前输送,在成型器两侧边有插边轮,支撑板将袋子撑开成四方形,并由插边轮将方形袋子左右两侧面沿中间线折入,使左右两侧折成M字形。成形过程如图2所示。袋子的成型包括导向段4个空间平面、成型段2个空间平面和4个空间曲面,一共10个面组成。10个面在相应空间上有10条相交曲线。

图 1 内置式M边成型器模型图
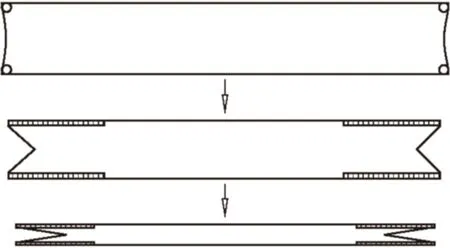
图 2 塑编袋成型示意图
建立如图3所示的空间坐标系,以ZOY为分界面,将模型分为导向部分和成型部分。Y方向为塑编袋宽度方向,X方向为袋子长度方向,Z轴为袋子的高度方向,由于袋子关于XOZ面对称,为了节约分析量,只选取Y≥0的部分进行研究。

图 3 塑编袋成型模型
2 塑编袋导向段曲面的数学模型
以Y轴为分界线,在X≤0为袋子成型前的导向部分,主要将筒状袋子撑开成四方形。如图4为导向段模型图,在该区域内共有3个面,即导向上表面CDVU(Σ1)、导向侧面DD′V(Σ2)、导向下表面C′D′UV(Σ3)和2段直线DV(I1)、D′V(I2),设塑编袋卷料的宽度为L,DD′的高度为a,这两个参数由袋子规格确定,导向段长度为L1。由于袋子在成型过程中,纵向和横向都不发生伸长和缩短,所以CD=(L-a)/2。
2.1线段I1、I2的空间方程
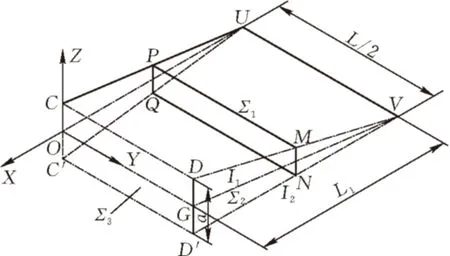
图 4 袋成型导向部分参数设置图
DM=λDV(λ∈[0,1])
即
所以线段的
(1)
I2与I1关于XOY面对称,所以其方程式为:
(2)
2.2空间平面Σ1、Σ2、Σ3的方程
在平面上任取一点T(x,y,z),由于CT,DC,DV共面,所以

此即
即可以得出平面Σ1的方程:
(3)
平面Σ1与Σ3关于XOY对称,则其方程式为:
(4)
同理,可求得平面的空间方程式:
(5)
3 成型段曲面的数学模型
塑编袋成型部分的空间立体图及所设定的各个参数见图5。该区域内包括两条空间直线DI(I3)、D′I(I4),一条空间曲线GL(I5),2个平面成型上表面CDIH(Σ4)、成型下表面C′D′HI(Σ7),和2个曲面DJLI(Σ5)、D′JLI(Σ6)。其中两个曲面Σ5、Σ6是成型的关键部分,也是本文的主要研究对象。设成型段的长度为L2,HI为成型的终止线,由于袋子在成型过程中在各个方向均不发生变形,所以塑编袋撑开的高度DG与M边折入的深度LI相等,即DG=LI, 在DI上任取一点S,并过点S作平面STS′R′R//ZOY,ST与XOY面之间的夹角为α。I点坐标为(L2,(L-a)/2,0),L点坐标为(L2,(L-a)/2,0)。

图 5 成型段参数设置图
3.1空间直线I3、I4的方程
设点S的坐标(x,y,z),DS与DI共线,因此
DS=λDI(λ∈[0,1])
即
所以的
(6)
I4与I3关于XOY面对称,即方程为:
(7)
3.2空间平面Σ4、Σ7的方程
由C,D,H三点可以确定平面的方程式,设平面任意一点为M(X,Y,Z),则有:

此即
所以Σ4的平面方程为
(8)
Σ7与Σ4关于XOY平面对称,Σ7的平面方程式为
(9)
3.3空间曲线I5的方程

图 6 M边成型断面图
由于两侧成型面在空间上是扭曲面,其数学方程式无法直接求得,所以采用间接的方式。将空间直角坐标系Oxyz进行平移,沿Y轴正向移动(L-a)/2,得到新的坐标系O′x′y′z′,如图6所示,坐标系的平移公式为:
通过在X轴方向上截面图可以观察到侧边逐渐由垂直渐变成水平,其渐变角度是本文所要讨论的重要参数。截取若干个断面图将其重叠到一起(图7)。

图 7 渐变角断面叠加图

所以有
由此可得出
所以T点在直角坐标系OXYZ中的坐标为:
即T点的坐标关系式为
可以求出成型曲线I5的方程式:
(10)
曲线I5即为椭圆曲线。
3.4空间曲面Σ5、Σ6的方程
在线段ST上取一点P(X1,Y1,Z1),SP与ST共线,因此
SP=λST
即

所以
(11)
此即为曲面Σ5上任意一点的坐标关系式,将式(11)化简为曲面Σ5的方程式:
其中

(12)
Σ7与Σ5关于Oxy面对称,所以Σ7的方程式为:
(13)
4 渐变角度参数变化关系研究
塑编袋M边成型数学模型当中所包含的参数有:α、a、L1、L2、L。这些参数当中L、a参数是根据产品规格确定的,其余参数则要根据安装要求在设计过程中确定。这些参数之间并非完全相互独立的,其中最为关键的参数是渐变角度α与L2之间的关系。
根据式(11)的推导公式,可以得出渐变角度α与x之间的关系式:
(14)
(15)
(16)
(17)


在x=0处取得最小值,即为
由以上分析可得出在x=0处的角度变化率为-∞,袋子的成型速度最快,即此处存在着柔性冲击;在x=0处的角加速度为-∞,袋子在此处存在着刚性冲击。所以成型器在此处的结构是存在问题的,应该加以优化,解决方案是将位于x=0处的交接线用曲线进行代替,由于篇幅有限,优化方案不在这里做详细分析。理论上L2的值越大越好,但成型的长度过大又会导致成型器空间尺寸过大,插边轮的个数增加,成型器的制作成本也相应提高。
5 进一步讨论
由式(10)、(11)、(12)可以确定成型曲面及曲线在空间中的位置,进而可以得出内置支撑板的调整方向和插边轮的安装位置,根据要求制作的袋子尺寸规格可以首先确定L和a的数值,对于不同的袋宽和M边深度,成型器也要做出相应调整,所以成型器在设计上可以考虑内置支撑板做成宽度和高度可调整型,插边轮在Y方向上做成可调型以满足M边深度的变化。
其次,可以根据导向段的长度来确定插边轮的个数,在不同位置的插边轮直径以及轮缘形状。
6 结束语
1)塑编袋M边成型数学模型共由10段不同的空间曲线组成,其中8段为空间直线;
2)塑编袋M边成型的空间曲面共有10个空间曲面,分为导向段和成型段,其中导向段有4个空间平面;成型段有2个空间平面和4个空间扭曲面。
3)渐变角是M边成型数学模型中的重要研究参数,渐变角的变化规律由导向段长度L2和x来确定,进而又能够确定插边轮的直径和轮缘形状。
4)M边成型曲面、成型曲线都可以用准确的数学方程式表达,因而可以利用计算机建立其三维模型,进而用现代加工制造技术来制造。
[1]许林成,彭国勋. 包装机械 [M] :长沙:湖南大学出版社,1989.12.
[2]徐红帅.翻领制袋成型器以直代曲的数学建模及成型工艺研究 [D].无锡:江南大学,2013.
[3]龚昇.简明微积分[M].北京:高等教育出版社,2006.
[4]周一届,蔡和平. 矩形翻领成型器曲面研究[J].包装工程,2004,25(1):18-19,26.
[5]朱鼎勋.空间解析几何学[M].北京:北京师范大学出版社,1985.
[责任编校: 张众]
Research of the Curved Surface of Packing Bags During M-Brim Forming
DENG Yuanchao, LIU Fang
(SchoolofMechanicalEngineering,HubeiUniversityofTechnology,Wuhan430068,China)
By analyzing the curve and the curved surface of packing bags in M-brim forming process, the mathematical models of the space carve and carve surface during the forming process of packaging bags were brought forward. On the basis of analyzing the continuous forming process of the packaging bags, the variety law of the forming gradient angle was obtained, which provided the mathematical evidence for manufacturing the M-brim shaper.
M-brim shaper; M-brim curved surface; gradient angle; mathematical models
2016-03-07
邓援超(1963-), 男, 湖北荆州人,湖北工业大学教授,研究方向为机械设计及理论
刘放(1991-),女,湖北宜昌人,湖北工业大学硕士研究生,研究方向为机械设计及理论
1003-4684(2016)04-0001-04
TB43
A

