改进的Morlet小波变换在储集层预测中的应用

齐　宇，梁建设，柳迎红，喻梓靓，陈思路

改进的Morlet小波变换在储集层预测中的应用

齐宇，梁建设，柳迎红，喻梓靓，陈思路

（中海油研究总院，北京100028）

Morlet小波是时频域内具有最好分辨率的小波。介绍了小波变换的方法，选取Morlet小波为母小波，引入一个控制小波函数带宽的参数c2加以改进，并研究了参数c2的变化对小波函数的影响，将改进的Morlet小波变换应用于地震物理模型发现，分频处理后的地震数据刻画目标体更为清晰，实例应用结果表明，改进的Morlet小波变换分频处理方法可以有效地提高储集层预测精度。

改进的Morlet小波变换；小波带宽；分频处理；储集层预测

提取和分析频率信息对于储集层预测和烃类检测极为重要。文献［1］提出用短时傅里叶变换方法刻画不同频率下河道展布特征后，许多学者利用此方法进行分频处理，取得了丰硕的研究成果。但是，短时傅里叶变换采用固定的窗口，无法兼顾高频与低频信号，对于非平稳性的地震信号效果并不明显。

小波变换是一种时间窗和频率窗都可以改变的时频局部化分析方法，享有“数学显微镜”的美誉。Morlet小波与地震子波具有相似性，可以通过伸缩、频移和调制来匹配实际地震数据，非常适合于地震信号的时频分析，因此得到了快速发展。文献［2］和文献［3］利用Morlet小波变换方法提高了地震资料的分辨率。文献［4］选取Morlet小波，对地震资料进行多尺度分析，将Morlet小波变换分频处理技术运用到致密气层预测中，取得较好的效果。在常规Morlet小波的基础上，中国学者提出了改进方法［5-7］，即引入一个参数c2控制小波函数的带宽，但是对于此参数如何控制小波函数的波形却鲜有报道。本文介绍了小波变换的原理，给出了改进的Morlet小波的数学公式，分别取参数c2为1，4，6和8，研究了Morlet小波函数的波形变化。结果表明，当c2为6时，改进的Morlet小波与雷克子波相似，可以较好地匹配地震信号，有利于分频处理，当c2为8时，其波形基本不变，因此参数c2取6.将改进的Morlet小波变换分频处理方法运用于西非尼日尔盆地南部深水A油田，有效提高了储集层预测精度，取得了良好的应用效果。

1　小波变换方法

1.1小波变换原理

小波变换在时频域具有表征信号局部特征的能力，它继承和发展了短时傅里叶变换局部化思想，同时又克服了窗口大小不随频率变化的缺点，提供一个时间窗口和频率窗口都可变的时频局部化分析方法［8-11］，具有多分辨率的特点。

对于任意一个平方可积函数f（t），其连续小波变换的定义为

不同的尺度参数a和平移参数b构成的小波基函数为

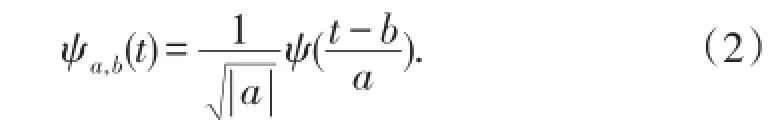
尺度参数a为1时，小波基函数的频率窗口既不拉伸也不收缩，只是平移；a大于1时，小波基函数的时间窗口拉伸，其频率窗口变窄并向低频方向移动，频率分辨率越高，时间分辨率越低；a为0～1时，小波基函数的时间窗口压缩，其频率窗口展宽并向高频移动，频率分辨率越低，时间分辨率越高。大的尺度参数对应低频端，小的尺度参数对应高频端。平移参数b也叫时间参数，取不同值时，窗口位置不同。

1.2改进的Morlet小波函数

Morlet小波是时频域内分辨率最高的解析小波，其实部与虚部有90°相移，易于得到频率、相位等信息［12-13］。

Morlet小波的数学表达式为

对常规Morlet小波进行修改，引入一个参数c2调节Morlet小波函数的带宽，（3）式改写成

但此时的Morlet小波直流分量不为零，即当小波函数的傅里叶变换结果不为零，需要加上适当的修正项

当ω2/4c2足够大时，修正项与计算机舍入误差有相同的数量级，此时修正项可以省略［5-6］。当c2为1时，即为常规的Morlet小波公式，可以看出小波函数的旁瓣较多。分别取c2为4，6和8，使改进的Morlet小波数学公式中-c2/2为整数，计算结果显示精度高。结果表明，参数c2起到了调节作用，随c2取值的增大，改进的Morlet小波的主峰能量不变，但旁瓣数量变少、能量变弱，频宽增加。当c2分别为6和8时，小波函数波形与雷克子波相似，波形变化较小，有利于匹配地震信号（图1）。本文参数c2取6，改进的Morlet小波公式为

根据褶积理论，无噪声的地震信号可以看成是反射系数与地震子波褶积的结果。设计一个共计10道，每道有4个间距相等、数值均为0.1的反射系数的楔形模型。随着道号的增加，后1道相比前1道反射系数间距依次增加2 ms，即第1道4个反射系数间距均为2 ms，则第2道4个反射系数间距均为4 ms，第10道4个反射系数间距均为20 ms（图2）。采用峰值频率为20 Hz、采样间隔为1 ms的雷克子波进行褶积，得到地震记录（图3）。从图3中可以看出，楔形模型出现了2种不同的反射波波形：①单层厚度较小时，即模型的1—5道地震记录只出现了一个单峰复合波；②单层厚度较大时，即模型的6—10道地震记录为双峰复合波，楔形模型的顶部和底部出现反射同相轴，内部界面并没有出现。

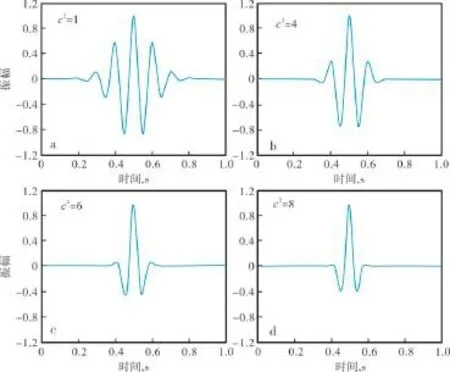
图1　c2取不同值时的Morlet小波波形

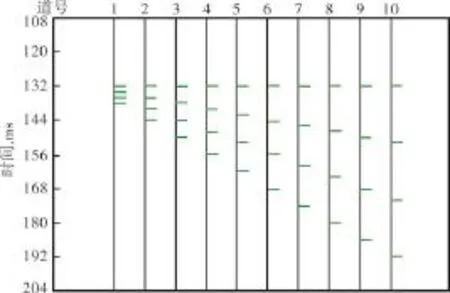
图2　反射系数楔形模型

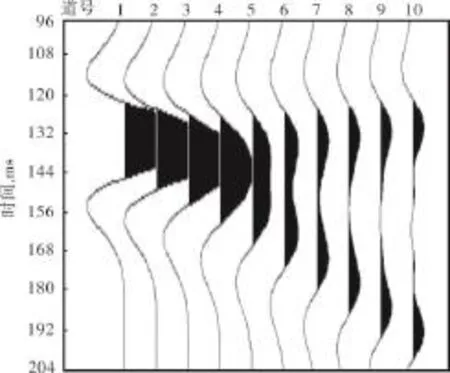
图3　楔形模型地震记录

为了验证改进的Morlet小波提高分辨率的能力，分别提取模型第5道和第9道2种不同的反射波波形。第5道分频频率大于27 Hz时，分频处理记录表现为双峰单谷的复合波，尽管只能分辨模型的顶界面和底界面，但是与原始地震记录相比，分辨率仍然得到提高（图4）；第9道分频频率大于47 Hz时，分频处理记录出现了4峰3谷的波形特征，其波峰对应地层界面的位置，从反射波波形上可以准确分辨出地层（图5）。

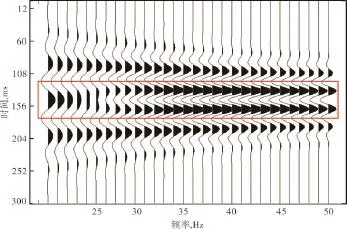
图4　楔形模型第5道分频处理记录

图5　楔形模型第9道分频处理记录

2　实际应用

2.1模型地震记录分频处理

设计4个砂体侧向对接的地震物理模型，具体参数如图6所示。根据时间域地震数据体目的层解释结果，在1 250 ms处分别提取了均方根振幅切片和改进的Morlet小波变换50 Hz频率调谐体切片（图7）。由图7可以看出，均方根振幅切片上砂体①和砂体②的边界形态模糊，而改进的Morlet小波变换50 Hz频率调谐体切片清晰地刻画出了砂体①和砂体②的边界。结果表明，频率调谐体切片在刻画砂体横向变化、展现沉积特征方面效果更佳。

图6　砂体侧向对接的地震物理模型剖面（a）及平面（b）展布

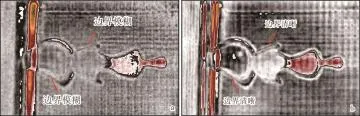
图7　地震物理模型地震数据均方根振幅切片（a）和改进的Morlet小波变换50 Hz频率调谐体切片（b）

2.2实际资料分频处理

以西非尼日尔盆地南部深水A油田为例，此油田处于区域拉张和挤压应力转换带，是泥底辟作用形成的大型背斜，被生油凹陷环绕，具有优越的油气成藏地质条件。目的层为新近系阿格巴达组，自上而下可分为A—H共8个油组，其中A油组为主力油组，为海退环境下形成的深水海底扇浊积水道沉积。

位于深水A油田背斜翼部的A井钻遇浊积水道沉积的A油组储集层，岩性以砂岩为主，夹泥岩，自然伽马曲线呈箱形，是一套优质储集层。但在过A井A油组的常规地震剖面上，浊积水道反射特征模糊，下切充填现象不明显。采用改进的Morlet小波进行分频处理后发现，地震剖面上出现了顶平底凸的“U”形反射特征，浊积水道下切及内部上超充填特征明显，分频处理剖面对浊积水道识别能力增强（图8）。

图8　西非尼日尔盆地南部深水A油田A井原始地震剖面（a）和改进的Morlet小波变换60 Hz分频处理剖面（b）对比

平面上，均方根振幅切片显示，A井位于浊积水道外侧（图9a），但实际上，此井钻遇浊积水道沉积的A油组储集层，均方根振幅切片解释结果与钻井结果矛盾；Morlet小波变换60 Hz频率调谐体切片上，浊积水道成像效果虽有提高，但是浊积水道的内幕细节不清，边界模糊（图9b）；改进的Morlet小波变换60 Hz频率调谐体切片上，浊积水道的刻画更清晰，砂体发育且连续性好，浊积水道展布和迁移特征明显，切片显示结果与实钻结果吻合，预测精度明显提高（图9c）。

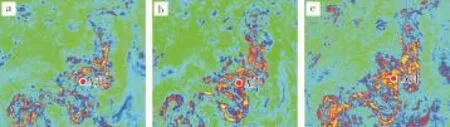
图9　西非尼日尔盆地南部深水A油田地震属性切片对比

3　结论

（1）改进的Morlet小波是在常规Morlet小波的基础上，引入一个参数c2控制其带宽，使小波函数的形式更加灵活，通过改变参数可以使Morlet小波更能符合地震子波的特征。

（2）将改进的Morlet小波变换分频处理技术运用于地震物理模型与西非尼日尔盆地南部深水A油田地震资料，结果表明，分频后的数据分辨率提高，目标体成像更为清晰，提高了储集层预测精度。

符号注释

a——尺度参数，a＞0；

b——平移参数；

c2——控制Morlet小波函数带宽的参数；

i——虚数；

t——时间，s；

W（a，b）——小波变换系数；

ψa，b（t）——小波基函数；

ψ（t）——Morlet小波函数；

ψ（1t）——改进的Morlet小波函数；

ψ（2t）——加上适当修正项的改进的Morlet小波函数；

ω——角频率，rad/s；

＜（ft），ψa，（bt）＞——（ft）和ψa，（bt）的内积。

［1］PARTYKA G，GRIDLEY J，LOPEZ J.Interpretational applications of spectral decomposition in reservoir characterization［J］.The Leading Edge，1999，18（3）：353-360.

［2］马朋善，王继强，刘来祥，等.Morlet小波分频处理在提高地震资料分辨率中的应用［J］.石油物探，2007，46（3）：283-287. MA Pengshan，WANG Jiqiang，LIU Laixiang，et al.Application of Morlet wavelet frequency-division processing in enhancing the seismic data resolution［J］.Geophysical Prospecting for Petroleum，2007，46（3）：283-287.

［3］马朋善，高秀花，汪桂春，等.小波分析在地震资料分频处理中的应用［J］.特种油气藏.2007，14（3）：35-38. MA Pengshan，GAO Xiuhua，WANG Guichun，et al.Application of wavelet analysis in frequency division processing of seismic data［J］.Special Oil&Gas Reservoirs，2007，14（3）：35-38.

［4］徐天吉，程冰洁.小波域地震信号的多尺度研究与应用［J］.石油天然气学报，2007，29（5）：80-83. XU Tianji，CHENG Bingjie.Research and application of multiscale seismic signal in wavelet domain［J］.Journal of Oil and Gas Technology，2007，29（5）：80-83.

［5］高静怀，汪文秉，朱光明，等.地震资料处理中小波函数的选取研究［J］.地球物理学报，1996，39（3）：392-400. GAO Jinghuai，WANG Wenbing，ZHU Guangming，et al.On the choice of wavelet functions for seismic data processing［J］.Acta Geophysica Sinica，1996，39（3）：392-400.

［6］吴小羊，刘天佑，唐建明，等.改进的Morlet小波频谱分析及在川西坳陷的应用［J］.石油天然气学报，2008，30（2）：242-245. WU Xiaoyang，LIU Tianyou，TANG Jianming，et al.Spectral decomposition based on modified morlet wavelet transform and application in western Sichuan depression［J］.Journal of Oil and Gas Technology，2008，30（2）：242-245.

［7］徐天吉，曹伦，程冰洁，等.基于地震波多尺度吸收属性的页岩气识别方法［J］.新疆石油地质，2016，37（1）：41-45. XU Tianji，CAO Lun，CHENG Bingjie，et al.Shale gas identification based on multi-scale and absorption attributes of seismic wave［J］. Xinjiang Petroleum Geology，2016，37（1）：41-45.

［8］齐宇，刘震，魏建新，等.基于小波变换的谱分解技术在地震模型解释中的应用［J］.新疆石油地质，2010，31（3）：417-419. QI Yu，LIU Zhen，WEI Jianxin，et al.Application of wavelet transform-based spectral decomposition technique to seismic model interpretation［J］.XinjiangPetroleumGeology，2010，31（3）：417-419.

［9］张德丰.MATLAB小波分析［M］.北京：机械工业出版社，2009. ZHANG Defeng.Matlab wavelet analysis［M］.Beijing：China Machine Press，2009.

［10］黄捍东，张如伟，郭迎春.地震信号的小波分频处理［J］.石油天然气学报，2008，30（3）：87-91. HUANG Handong，ZHANG Ruwei，GUO Yingchun.Wavelet frequency-division process for seismic signals［J］.Journal of Oil and Gas Technology，2008，30（3）：87-91.

［11］吴爱弟，曹思远.利用平衡双正交多小波变换进行地震数据去噪与压缩［J］.石油地球物理勘探，2004，39（6）：636-640. WU Aidi，Cao Siyuan.Noise-elimination and compression of seismic data using balanced biorthogonal multi-wavelets transform［J］. Oil Geophysical Prospecting，2004，39（6）：636-640.

［12］MORLET J，ARENS G，FOURGEAU E，et al.Wave propagation and sampling theory-part II：sampling theory and complex waves［J］.Geophysics，1982，47（2）：222-236.

［13］MORLET J.Sampling theory and wave propagation［R］.51th SEG Annual International Meeting，Los Angeles，USA，1981.

（编辑潘晓慧杨新玲）

Application of Modified Morlet Wavelet Transform in Reservoir Prediction

QI Yu，LIANG Jianshe，LIU Yinghong，YU Ziliang，CHEN Silu
（CNOOC Research Institute，Beijing 100028，China）

Morlet wavelet possesses the highest resolution in time frequency domain.This article presents a wavelet transform method，selects Morlet wavelet as mother wavelet，introduces a parameterc2controlling the bandwidth of wavelet functions which will be modified later，and studies the influences ofc2variation on wavelet functions.After the application of modified Morlet wavelet transform in seismic physical modeling，the seismic data after frequency division processing can provide more clear description of objectives.The case study shows that the modified frequency division processing method of Morelet wavelet transform can effectively improve the accuracy of reservoir prediction.

modified Morlet wavelet transform；wavelet bandwidth；frequency division processing；reservoir prediction

P631.443

A

1001-3873（2016）05-0598-04DOI：10.7657/XJPG20160519

2016-03-30

2016-06-30

国家科技重大专项（2011ZX05060）；中海石油科技攻关项目（YXKY-2015-ZY-08）

齐宇（1984-），男，新疆克拉玛依人，工程师，油气勘探，（Tel）010-84525307（E-mail）qiyu@cnooc.com.cn