基于马尔可夫模型的交叉口两难区自适应控制

刘诗福, 张　轮, 杨文臣, 王　铮

(同济大学 道路与交通工程教育部重点实验室， 上海 201804)



基于马尔可夫模型的交叉口两难区自适应控制

刘诗福, 张轮, 杨文臣, 王铮

(同济大学 道路与交通工程教育部重点实验室， 上海 201804)

提出一种基于马尔可夫模型的信控交叉口两难区自适应控制方法.根据实时监测的两难区内车辆数据，采用马尔可夫模型主动预测陷入两难区内车辆数的概率分布，提出采用基于n近邻的状态转移矩阵的更新框架，并综合考虑相位时长，建立相位延长和切换时两难区内当量车辆数的计算模型，进而以相位切换的风险概率为准则，采用即时决策的交通控制自适应调整相位时长.以广州市某交叉口进行VISSIM仿真实验，在不同强度的交通条件下，验证提出方法的效用并进行参数敏感性分析.仿真结果表明经过模型参数校准后，提出的控制方法在有效减少陷入两难区内的车辆数的同时，可减小交叉口的平均延误.

两难区； 自适应控制； 主动预测； 马尔可夫模型； 状态转移矩阵； 后悔率

城市信号控制交叉口的交通安全形势严峻.据NASS统计，全球发生在交叉口的事故约占事故总数的25%[1]，而在2004年我国发生在交叉口的交通事故中，由交通信号灯引起的事故超过一万多件[2].交通信号配时方案的安全及合理设置，是信控交叉口交通安全保障的关键.目前，大多数交通控制系统综合考虑交通的损失及效益指标，根据交叉口交通需求的波动自适应调整配时方案，缺少面向交通安全的交通控制方法.国内外众多学者的研究和实践均表明：在不同流向通行权切换的过渡阶段，信控交叉口存在行车选择的两难区，两难区内的车辆数越多，闯红灯和急刹车引发的追尾、侧碰等潜在安全隐患越大.

Gazis等在1960年首次提出I型两难区[3]，并采用黄灯期间车辆到达停车线的安全距离进行定义.美国交通工程师协会ITE于1974年根据驾驶者在黄灯期间减速行为的统计分布定义了II型两难区[4]， 并采用车辆到达停车线的平均行驶时间进行量化.Chang等根据信号切换间隔对多类驾驶行为影响的数值分析，采用车辆到停车线的2～6 s行驶时间界定II型两难区的末端和始端位置[5].Bonneson等在2002年结合美国德克萨斯交通学院(TTI)的D-CS(两阶段控制系统)的研发和试点测试，提出II型两难区为车辆到达停车线前2.5～5.5 s的行驶时间区域[6].Adam等提出了一种基于强化学习的两难区自适应控制方法[7]，Li等提出了基于马尔可夫过程的两难区防护算法[8]，Abbas等通过机器学习方法来提高交叉口两难区的安全[9]，Feng等通过建立罗伯逊车队离散模型计算两难区内的车辆数[10].近两年，国内学者开始关注两难区问题，陈雪峰等采用正交试验法综合分析了信号协调条件下I型两难区的5类关键影响因素的作用机理[11].刘润乔等通过车载预警和改变黄灯时间来降低车辆陷入I型两难区事件的发生概率[12].沈家军等通过设计合理绿闪时长和道路限速来消除I型两难区的负面影响[13].

多位学者采用驾驶行为引导、黄灯时间优化、两难区预警、配时参数调整、车路协同等方法和技术研究了I型两难区控制问题，旨在通过驾驶行为的规范引导、信号过渡时间或是相位时长等配时参数的合理配置以期减少陷入两难区内的车辆数.在调整配时方案参数的研究方面，多数学者遵循感应控制基本逻辑，采用即时决策的交通控制系统动态调整相位绿灯时长，以减少在最大绿灯时间通过交叉口的交通量.但是，多数研究仅以两难区内存在的车辆数为条件进行逻辑决策，信号动作决策的逻辑并未综合考虑即时决策的信号动作对未来陷入两难区内车辆数的影响，仅依据“相位切换”两难区内期望的车辆数是否大于“相位延长”两难区内期望的车辆数，相位切换较频繁[8]；同时，所提出方法参数一旦标定便不再发生改变，不能有效响应交叉口不同条件下交通流的波动[6]，控制模型或参数将随着交叉口交通模式的变化而逐渐老化.

不同的绿灯过渡信号(黄灯[3,11]和绿闪-黄灯[13]等)将带来不同复杂层次的两难区控制问题.据调查，虽然在我国一些城市采用绿闪信号作为一种附加显示方式，但绝大多数信控路口不设置绿闪信号.为此，本文以设置黄灯作为绿灯过渡信号的信控路口为研究对象，以减少陷入两难区内的车辆数为目标，从“高效、合理、有序”自适应调整配时参数的角度，提出一种基于马尔可夫模型的两难区自适应控制方法(MD-ATSC)，以广州市某交叉口进行VISSIM仿真实验，在多种交通条件下对提出的模型的效用进行检验.

1　两难区定义

在黄灯启亮时刻，驾驶者在进口道行车面临两种选择：通过交叉口或者在停止线停车等待.此时，如果车辆在黄灯期间既不能顺利通过交叉口，也不能在停车线前顺利停车，则称车辆处于“两难区”.在两难区内，“不能顺利通过停车线而选择急刹车”的车辆容易引发追尾事故，“不能停在停车线前而强行闯红灯”的车辆则容易引发侧碰事故.因而，两难区威胁交叉口的交通安全，应尽可能消除.如图1所示，国际上存在两类两难区的定义.图中，D1为顺利通过停车线的最大距离，D2为安全舒适停在停车线前的最小距离，D3为10%驾驶者选择减速停下，D4为90%驾驶者选择减速停下.

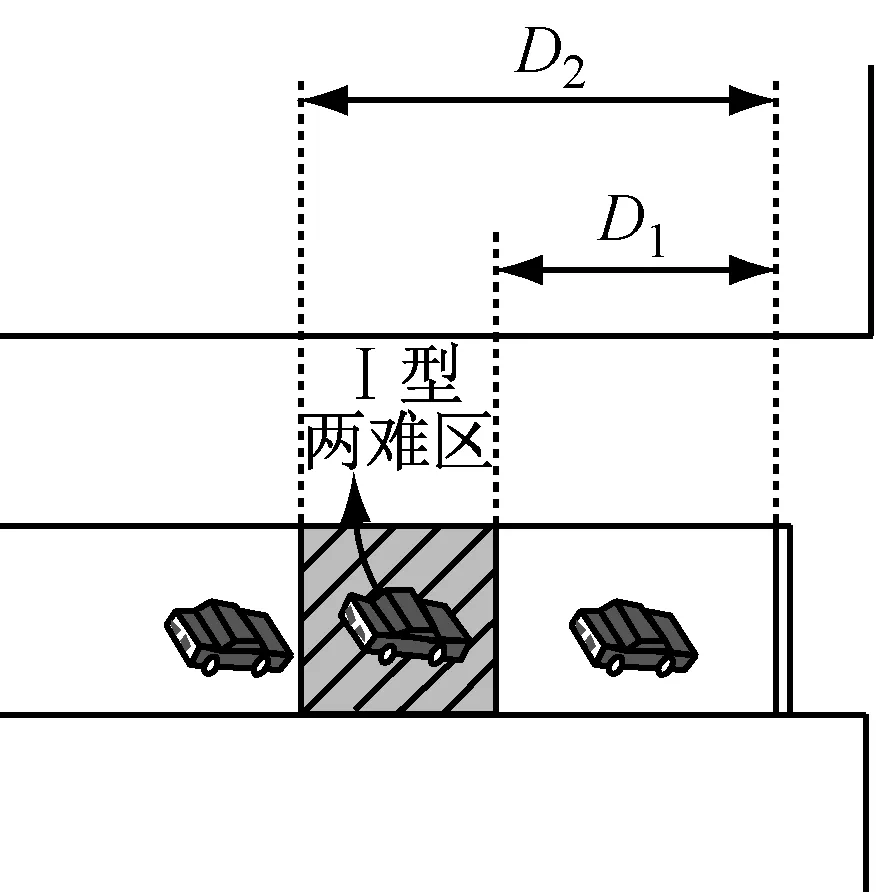
(1)I型两难区：

I型两难区根据黄灯期间的安全停车距离进行定义，表征“既通不过也停不下来”行车两难区域，即面对黄灯时驾驶者既不能安全通过交叉口也不能在停车线顺利停车的区域.其始端采用车辆在黄灯结

束前安全舒适地刹车停在停车线的最小距离，而末端采用车辆在黄灯结束前顺利通过停车线的最大距离[11].记I型两难区的长度为dI，则I型两难区的范围如式(1)所示：

(1)

式中：v为车辆驶入交叉口的平均速度，m·s-1；ty为黄灯时间,s；tr为驾驶者看到黄灯并开始减速的反应时间,s，a为车辆减速度，m·s-2.

(2)II型两难区：

II型两难区根据黄灯期间驾驶者减速停车驾驶行为的统计分布特性进行定义，表征“既可能行驶也可能停下”的行车两难不确定性区域.Zegeer等提出II两难区的始端和末端分别是90%位和10%位驾驶者减速停车的位置，始端到停车线的平均行驶时间约为5 s[14].美国TTI通过D-CS系统的研发和实地布署应用的测试，建议II型两难区的范围为距离停车线前2.5～5.5 s的行驶区域[6].据此，II型两难区的范围如式(2)所示：

(2)

式中：dII为II型两难区的位置.

在我国信控交叉口，黄灯时间为3 s，取驾驶者的反应时间为2～3 s，车辆平均减速度为3.5 m·s-2[15].按照《城市道路设计规范(CJJ37—90)》，交叉口内的设计车速应该按照各级道路路段设计车速的0.5～0.7倍计算，而城市主干路的设计车速为30 ～60 km·h-1，所以交叉口设计的平均车速为15～42 km·h-1，根据式(1)—(2)分别计算得到I型和II型两难区的最大范围如式(3)所示：

35m≤dI<54.44m

(3a)

29.17m≤dII≤64.17m

(3b)

由式(3)可知，I /II型两难区上均表征一个空间范围或空间分布，且I两难区位于II两难区的范围之内，减少陷入II型两难区内的车辆数将更好地减小车辆两难决策的概率，进而降低事故发生概率.同时，I型两难区的安全停车距离受不同路口的行驶条件影响，不同路口间没有统一的判定准则；而II型两难区以车辆距停车线的行程时间作为两难区始端和未端的判别依据，具有较好的普适性.综上分析，本文选取II型两难区为分析对象.

2　基于马尔可夫模型的交通状态预测

2.1交通状态定义

(4)

(5)

式中：DVl为f流向所含车道l的两难区内车辆数.在当前相位遵守最小/最大绿灯基本约束的前提下(即进入即时决策交通控制逻辑)，通过在II型两难区的起点和终点位置布设线圈检测器进行采集.记Nmax为陷入车道内两难区的最大车辆数，采用式(6)计算.

(6)

2.2马尔可夫状态预测

(1) 状态转移矩阵

马尔可夫模型研究某一时刻的初始状态及其状态之间转移的概率关系，预测事件的未来状态，在交通领域有着广泛的应用.陷入两难区内的车辆数在时间上离散，状态转移随机，且只与当前状态相关，满足马尔可夫模型的离散性、随机性和无后效性的特征，故可采用马尔可夫模型预测信控交叉口每一个流向的两难区内交通状态的演化规律[7-8].记f流向的状态转移概率矩阵采用Pf描述，如式(7)所示.

(7)

(8)

式中：mi为f流向中状态i转移到状态j的次数；Mi为f流向中状态i出现的总次数；T为系统工作时间，I(ψ)为定义条件存在的0-1指示函数，如式(9)所示.

(9)

(2)马尔可夫状态预测

(10)

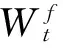
(11)

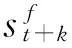
(12)

2.3状态转移矩阵更新

每个流向的状态转移矩阵与交叉口的交通条件相关，且状态转移的知识会随着控制时间的增加而老化.为有效表征交叉口每一流向的状态转移关系，保证系统对陷入两难区内车辆数的动态调控能力，必须滚动更新各流向的状态转移矩阵，更新的架构如图2所示.

图2　基于n近邻的状态转移矩阵的更新框架

(1)不同交通条件下状态间转移规律差异较显著，为更精细地描述不同交通条件下状态转移关系，系统将1 d按照整点划分为24个时段，且在每天的一个控制时段结束后，滚动更新该时段下的状态转移矩阵.

(2)由于交叉口每一流向在每天相同时段内的交通流具有较好的相似性，为了同时兼顾学习系统最新访问到的转移知识和避免短时交通流带来的偏差，需对当前时段观察到的转移知识进行修正.

(13)

(14)

即采用历史邻近n天内同一时段的状态转移频数的均值更新该时段下的状态转移矩阵.

3　两难区自适应交通控制

3.1自适应控制系统结构

两难区自适应交通控制系统的结构如图3所示：“马尔可夫模型的交通状态预测”模块采用马尔可夫预测模型在线学习，预测每一流向两难区内交通状态演化.“状态转移矩阵更新”模块用于对各流向两难区状态转移知识的更新.“MD-ATSC信号控制器”根据预测当前相位两难区内的当量车辆数，即时决策信号动作的输出(延长或切换).“历史数据库”模块用于不同交通条件下数据采集以及修正优化后的存储与挖掘.

图3　两难区自适应交通控制系统

3.2两难区内当量车辆数

(15)

式中：Tavg为控制时段内的平均周期时长.

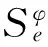
(16)

(17)

其中

(18)

3.3切换风险概率

综合考虑相位延长和切换两种条件下当前相位陷入两难区的当量车辆数，定义相位切换两难区内当量车辆数的比例Rq为相位切换的风险概率，由式(19)计算：

(19)

式中：qend为切换绿灯条件下当前相位两难区车辆数的小时当量值，由式(15)计算；qextend为延长绿灯条件下当前相位两难区车辆数期望值的小时当量值，由式(16)计算.

如果相位切换的风险概率小于指定的决策阈值，则顺序切换至下一相位.相位切换的概念模型如式(20)所示：

(20)

式中：λ为风险系数，控制当前相位切换的严格程度；λ值越小，相位中断的概率越大.

3.4控制算法设计

遵循最大周期及最大最小绿灯时间的原则，MD-ATSC系统即时决策的控制逻辑如下：

步骤1,对当前相位首先给予最小绿灯时间控制；

步骤2,在最大绿灯时间前，根据车辆检测器每Δe秒采集交叉口每一流向的交通数据，交通状态预测模块主动预测各流向陷入两难区内车辆数的概率分布，并按时段的划分存储于历史数据库，且在控制时段切换时，采用邻近n天滚动更新该时段下的状态转移矩阵；

步骤3,考虑当前相位持续时间，分别计算绿灯延长和绿灯中断两种条件下当前相位陷入两难区的当量车辆数，并计算“相位切换”的切换风险概率；

步骤4,根据切换风险概率，判断当前相位是否顺序切换至下一相位.

(1)如果切换风险概率小于决策阈值，结束绿灯并返回至步骤1；

(2)如果切换风险概率大于决策阈值，则相位绿灯时间延长Δe秒，判断相位累积时间是否超过最大绿灯时间，若仍小于最大绿灯时间，则返回至步骤2；反之，根据最大绿灯时间约束，修正延长时间，在最大绿灯时间后，顺序切换至下一相位，返回步骤1.

4　案例分析

4.1案例描述

以广州市天河区某交叉口作为模型的验证对象，该交叉口位于天河中央商务区(CBD)的商业中心，采用标准四相位进行多时段定时控制，具有交通流量大，交通事故多，高峰时段交通拥堵严重等特征.以VISSIM作为交通信号控制策略无偏的评价工具，搭建基于VISSIM的两难区自适应控制在线仿真平台，对提出的模型和算法进行验证，仿真平台的结构如图4所示.

4.2实验设计

(1)仿真场景

为考察提出方法在不同流量和交通流波动情况下的控制效果，抽取算法参数的取值，场景设计如下：① 仿真时长为6 h(00:00-6:00)，为模拟交叉口高饱和和低饱和等不同交通条件，进口单车道流量在200～700辆·h-1·车道-1变化.② 为模拟交叉口短时交通流到达特性，在VISSIM的Routes中每隔10 min设置车辆的发车比例为15-11-17-22-16-19.③ 为丰富状态转移矩阵的知识，同时避免微观仿真结果受随机种子的影响，每种控制方法批量仿真30次(随机种子seed值取1～30)，每次仿真代表一个月内1 d的历史数据.

图4　两难区自适应控制VISSIM仿真平台

(2)仿真实验

实验对比分析两阶段的D-CS法(D-CS)和传统的定时控制方法(Fixed).D-CS系统是美国德克萨斯开发的两难区控制系统[6]，两阶段划分的时间阈值为25 s.6种流量水平下的定时控制方案采用英国交通运输研究所(TRRL)模型求解[16].实验参数的设置如下：最小绿灯时间Gmin为10 s，最大绿灯时间Gmax为60 s.风险系数λ为0.45，单位延长时间Δe为3 s，矩阵更新参数n为2.选取交叉口陷入两难区内的车辆总数评价交通安全，交叉口的平均延误评价控制效益.同时，定义后悔率统计分析不同交通状态下两难区信号决策的反悔概率.后悔率越低，信号决策的可信度越高.“切换和延长”两种信号动作的后悔率由式(21)计算：

(21a)

(21b)

4.3结果分析

(1)控制效能的对比

MD-ATSC系统的控制效果仿真结果如图5所示.整个仿真过程中，三种控制方法的陷入两难区内的车辆数和交叉口平均延误都随着交叉口交通需求的增加而增加.与Fixed(定时控制)和D-CS相比，MD-ATSC在减少两难区车辆总数方面的性能最好，其低流量下分别减少陷入两难区内的车辆数达90%和60%；而在高流量条件下也能分别达40%和15%.这是因为MD-ATSC能根据交叉口两难区状态，主动预测不同交通条件下两难区内车辆数的演化趋势，并综合考虑当前相位的持续时间自适应调整相位时长.而D-CS仅凭当前陷入两难区内的车辆数判定信号动作，没有预见两难区状态演化的能力，系统决策的后悔率高致使陷入两难区内的车辆数较多.

a 陷入两难区车辆数

b 交叉口平均延误

值得注意的是，MD-ATSC在显著降低陷入两难区内车辆数的同时，也能有效减小交叉口延误.与Fixed和D-CS相比，MD-ATSC减少交叉口平均延误达3%～20%：这是因为MD-ATSC在主动调控陷入两难区的车辆数的同时，通过引入当前相位的持续时间，综合考虑交叉口其他车流的通行需求，可更好地响应交叉口交通需求的变化.加之，D-CS的控制逻辑在高流量交通条件下容易采取最大绿灯时间控制，对交通需求波动的响应能力受限.

(2)矩阵更新参数n值

状态转移矩阵的更新直接反映控制器对实变交通流的自适应响应能力.在500辆·h-1·车道-1的场景下，东进口直行流向两难区内状态2向状态1转移的频数随n值的变化如图6所示.n值越大，历史数据中状态转移频数的平滑效果越显著，且受随机种子的影响，在第6 d和第24 d状态2向状态1转移的次数明显减少；在第11 d转移的次数明显增加.当n>2时，平滑后p21累积频数分布差异不大，且不能反映状态转移的突变信息，在新交通条件下状态转移知识呈现老化态势；而当n<2时，状态转移的突变信息对矩阵的影响较显著，容易造成系统决策输出的振荡.综合考虑新状态转移知识的学习及系统稳定性，研究取n值为2.

图6　不同n值下状态转移矩阵M21(东进口直行)的更新示意

(3)后悔率分析

后悔率一定程度上可反映交通信号控制器的可靠性和合理性.以进口道低流量(300辆·h-1·车道-1)和高流量(600辆·h-1·车道-1)的交通条件为例，系统决策的后悔率随陷入两难区内车辆数的变化如图7所示.在低流量条件下当前流向的两难区内没有车辆时，MD-ATSC系统切换当前相位的概率大；而当前流向陷入两难区内车辆数大于等于1辆时，系统预期后续各流向两难区维持低状态的概率大，延长当前相位的概率显著增大.而在高流量下当前流向陷入两难区内车辆数小于2时，系统切换相位的概率较大，这是因为在较高的交通条件下各流向预期两难区车辆数都较多；只在当前流向两难区内车辆数不少于2时，系统延长当前相位的概率大，并随着两难区内车辆数的增加而增大.在不同交通条件下仿真结果提示的相位决策知识与管理者的预期较相符.

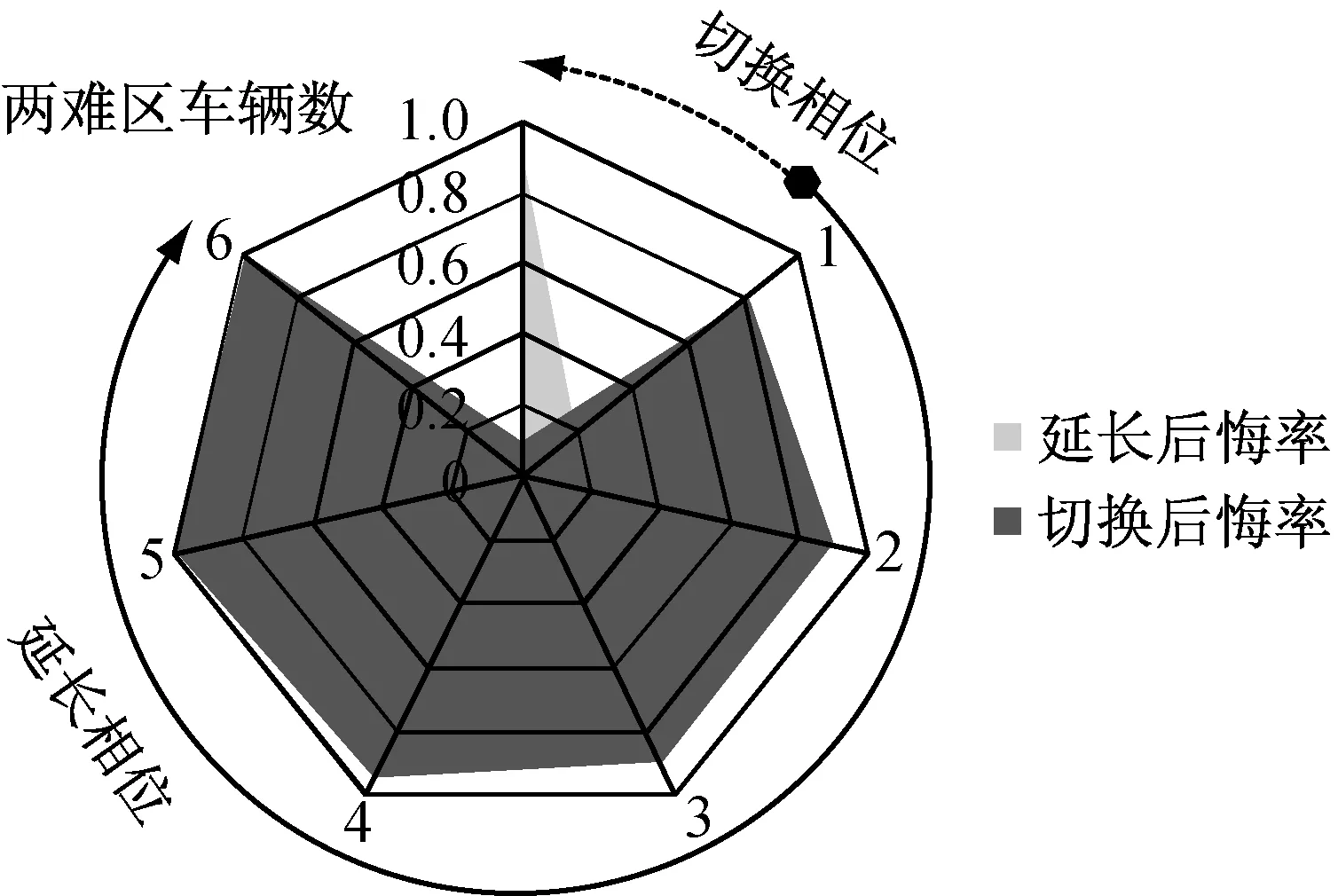
a 低流量下

b 高流量下

(4)风险系数分析

风险系数λ直接体现相位切换的严格程度.在三种不同的交通流量下，陷入两难区内车辆数在不同风险系数下的性能变化如图8所示.整体而言，陷入两难区内的车辆数随风险系数的增加呈抛物线分布的态势，可分为两个阶段.在阶段一，陷入两难区内的车辆数随着λ的减小而增大.这是因为风险系数越小，相位切换的条件越严格(倾向于延长)，系统只有在两难区内车辆数很少的状态下才切换相位，系统容易采取最大绿灯时间的控制，只能强制“接受”最大绿灯两难区内的车辆数而使陷入两难区内的车辆数增加.当λ的取值小于0.2时，系统只能期待两难区的车辆数为零时切换相位，在较高流量条件下，MD-ASTC的陷入两难区车辆总数较大.在阶段二，陷入两难区内的车辆数随着λ的增加而增加.这是因为风险系数越大，相位切换的条件越宽松(倾向于切换)，系统可在两难区内的车辆数较多的状态下切换相位，相位的频繁切换使车辆在交叉口的停车次数增多(尤其是高流量条件下)，增加的车辆陷入两难区的可能.当λ取值大于0.8时，系统在最小绿灯结束就切换相位，交叉口信号周期时长变短，MD-ASTC的陷入两难区的车辆总数大于定时控制.综上讨论，研究选取λ为0.45.

图8　不同风险系数下陷入两难区内的车辆数

5　结论

(1)两难区的存在威胁着交叉口的交通安全，采用马尔可夫模型主动预测陷入两难区车辆数的概率分布，提出了一种基于马尔可夫模型的两难区自适应控制方法.仿真结果表明：依托准确的马尔可夫状态转移的预测模型，即时决策交通控制方法在有效减少了两难区内的车辆数提升交通安全的同时，可降低交叉口的平均延误来提高交叉口的通行效率.

(2) 为兼顾学习系统最新访问到的转移知识和避免短时交通流带来的偏差，提出了状态转移矩阵的更新机制，将状态转移矩阵分时段滚动更新，可使系统学习到最新的两难区状态转移知识，更好地响应交通流的变化.

(3)提出面向两难区即时决策交通控制的后悔率指标，分析结果表明：相同两难区状态下，车流量越高，MD-ASTC的延长后悔率越高，切换后悔率越低.

(4)风险系数的取值与交通流特征相关，为了优化系统模型的预测框架，在不同的交通强度下，综合分析风险系数的敏感性，结果表明太高或者太低的风险系数将会导致方法的失效，合理的风险系数范围才能提高两难区自适应控制方法的性能.

[1]National Automotive Sampling System(NASS): General Estimates System(GES): Analytical User’s Manual 1988-2001[Z]. [S.l.]:NHTSA, U.S. Department of Transportation, 2011.

[2]中华人民共和国国家统计局.2004道路交通事故统计年报(汇总版)[M].北京:公安部交通管理局，2005.

National Bureau of Statistics of the People's Republic of China. 2004 Statistical Yearbook of road traffic accidents (summary version) [M]. Beijing:Ministry of Public Security Traffic Management Bureau, 2005.

[3]Gazis D, Herman R, Maradudin A. The problem with the amber signal light in traffic flow[J]. Operations Research, 1960, 8(1): 112.

[4]Parsonson P S, Roseveare R W, Thomas Jr J R. Small-area detection at intersection approaches[R]. [S.l.]: Traffic Engineering, 1974.

[5]Chang M S, Messer C J, Santiago A J. Timing traffic signal change intervals based on driver behavior[M]∥Transportation Research Record 1027. Washington D C: Transportation Research Board, 1985: 20-30.

[6]Bonneson J A, Middleton D, Zimmerman K,etal. Intelligent detection-control system for rural signalized intersections[R]. Austin: Texas Dept. of Transportation, 2002.

[7]Adam Z, Abbas M M, Li P,etal. Evaluating green-extension policies with reinforcement learning and markovian traffic state estimation[J]. Transportation Research Record: Journal of the Transportation Research Board, 2009(2128):217.

[8]Li Pengfei, Abbas M M. A Markov process based dilemma zone protection algorithm[C]∥Proceedings of the 2009 Winter Simulation Conference. [S.l.]:[s.n.], 2009: 2436-2445.

[9]Abbas M, Machiani S G, Garvey P M,etal. Modeling the dynamics of driver's dilemma zone perception using machine learning methods for safer intersection control[R]. [S.l.]:[s.n.],2014.

[10]Feng Y, Head K, Ma W. Estimating vehicles in the dilemma zone and application to Fixed-Time coordinated signal optimization[J]. Transportation Research Record: Journal of the Transportation Research Board, 2014 (2439): 62.

[11]陈雪峰，马万经. 信号协调条件下交叉口两难区仿真分析[J]. 交通科学与工程,2011,27(3):87.

CHEN Xuefeng,MA Wanjing.Simulink-based analysis of the dilemma zone of intersection under the coordinated control[J].Journal of Transport Science and Engineering, 2011,27(3):87.

[12]刘润乔,韩加蓬,刘洪光.两难区影响因素与控制策略[J].山东理工大学学报:自然科学版,2015(2):51.

LIU Runqiao,HAN Jiapeng, LIU Hongguang. Influencing factors and control strategies of dilemma zone[J].Journal of Shandong University of Technology:Natural Science Edition, 2015(2):51.

[13]沈家军,王炜.绿闪信号作用下城市道路交叉口两难区研究[J].交通运输系统工程与信息,2015(3):70.

SHEN Jiajun,WANG Wei.Dilemma zone of urban intersection based on effect of flashing green[J]. Journal of Transportation Systems Engineering and Information Technology, 2015(3):70.

[14]Zegeer. Effectiveness of green-extension systems at high-speed intersections, research report 472, Division of Research[R]. Lexington: Kentucky Bureau of Highways, 1977.

[15]周商吾. 交通工程 [M]. 上海：同济大学出版社，1987.

ZHOU Shangwu. Traffic engineering [M] Shanghai: Tongji University Press, 1987.

[16]Webster F V． Traffic signal settings[R]． London: Road Research Laboratory，1958．

Markov Model Based Adaptive Traffic Signal Control for Dilemma Zone at Signalized Intersections

LIU Shifu, ZHANG Lun, YANG Wenchen, WANG Zheng

(Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China)

This paper presents a markov model based adaptive traffic signal controller for dilemma zone(DZ) at signalized intersections. With the real-time traffic data of vehicles trapped in the DZ, the probability distribution of vehicles in the DZ is predicted using markov model, while the state-transition matrixes is rolling updated using then-nearest neighbors algorithm. Taking the phase time and the predicted trapped vehicles into account, the model of equivalent number of vehicles in the DZ is developed, and then under the real-time decision signal control strategy, the green phase time is adjusted accroding to the defined risk probability of switching phase. Extensive experiments were conducted on a typical isolated intersection in Guangzhou via online VISSIM simulation under different traffic conditions, and the sensitive analysis of model parameters were analyzed in detail. The simulation results have demonstrated that with the calibriation of model parameter, the developed controllers has the great potential in the reduction of vehicles trapped in the DZ, as well as the average traffic delay.

dilemma zone; adaptive control; active prediction; Markov model; state transition matrix; regret rate

2015-07-23

国家“八六三”高技术研究发展计划(2012AA112307)

刘诗福(1993—)，男，博士生，主要研究方向为道路与机场工程、智能交通运输系统.E-mail:1151160@tongji.edu.cn

杨文臣(1985—)，男，工学博士，主要研究方向为人工智能，智能交通控制系统.E-mail:tongjiywc@gmail.com

U491.51

A