基于最小二乘法的椭圆拟合实时航迹矢量化方法

基于最小二乘法的椭圆拟合实时航迹矢量化方法

民航业的快速发展使得各地空管部门压力急剧增大，为了解决日益严峻的空中交通管制问题，本文提出实时航迹矢量化方法。该方法的原理为首先对实时雷达数据采用最小二乘法拟合航迹段，然后通过判定航迹段间的夹角，将航迹处理为直线段与曲线段的连接；最后通过椭圆拟合方法对实时航迹点预测，以及相应的偏差修正，以完成对于实时航迹的矢量化预测过程。对飞行航迹进行拟合的方法以最小二乘法最为普遍，最早的椭圆拟合方法源自最小二乘法，考虑随机产生的误差对数据的影响同时将这些影响以平方的形式最小化。通过实验计算近千条真实飞行航迹数据，得出基于最小二乘法的椭圆拟合实时航迹矢量化方法的误差在可控的范围内，是一种有效，可行的实时航迹矢量化预测方法。

航空运输行业的快速发展，为人们的出行提供了便利。但是随着空中交通流量的持续增长，航空延误、空域拥堵等问题时有发生，使得航空器冲突探测与解脱、进离场航班排序、 基于轨迹运行等空管自动化与智能化方法成为空中交通管理领域的研究重点，而如何快速准确的进行航空器飞行实时轨迹预测是实现上述方法的基础与保障。

目前飞行轨迹预测的方法主要有两种。第一种是基于混合估计理论实现的航迹预测，利用交互式多模型（IMM）算法通过对横向、纵向以及垂直方向三种状态估计加权求和实现随机线性混杂系统的状态估计，进而预测出航迹。第二种是基于航空器动力学及运动学模型， 利用各类机型的性能参数实现航迹的实时预测。如文献提出根据飞行阶段特点，用基本飞行模型构建水平航迹、高度剖面和速度剖面， 根据航迹特征点的飞行状态信息拟合生成完整的 4D 航迹。

上述提出的两类方法用于飞行轨迹的预测存在以下两种问题：一是航空器的飞行模拟状态需要随实际情况的变化而变化，而IMM算法中假设的模拟转换矩阵为固定值。二是在不考虑气象信息或不能准确判断航空器飞行意图的情况下，很难保证航迹预测的准确度。

为了解决上述问题，本文中根据已知的飞机航行轨迹，判断当前所处阶段为直线航行或曲线航行，估测后续飞行轨迹点，进而拟合出行进轨迹的方法。最后，再对因轨迹预测可能产生的偏差分情况分别进行纠正，形成一条符合实时环境状况、飞行器飞行特征和飞行意图的平滑的行进轨迹。

方法原理

拟合原理

最小二乘法最早被称为“回归分析法”，由著名统计学家道尔顿于1806年所创，当时作为一种数学优化技术，解决了日常生活中的计算问题。它通过最小化误差的平方和寻找数据的最佳函数匹配。在现在，通过这种方法可以对未知数据进行预测，并且极大化地减小误差，求得与真实数据误差最小的预测数据。常用来解决曲线拟合、最佳逼近、物体运动轨迹等问题。其他一些优化问题也可通过最小二乘法来解决。

当存在大量实验数据时，不能绝对要求拟合函数ϕ（x）在数据点（xi，yi） 处的误差，即为0，但为了使曲线尽量逼近真实数据点的变化趋势，将误差的平方和最小，这就是最小二乘法的原理。

航迹的分段

就典型的航空器飞行航迹来说，航空器一般都是以直线的飞行轨迹从一个航迹点飞行至另一个航迹点，或者在空中进行了转弯等飞行动作，以曲线的飞行轨迹从一个航迹点飞行至另一个航迹点，这些航路点信息可以从领航计划报（filed flight plan message，FPL）中得知。即航迹可由一系列的直线飞行航迹段和曲线飞行航迹段组成。

直线飞行航迹段是飞行过程中的最简单的部分，如图1所示，P1（x1，y1，z1）点和P2（x2，y2，z2）点分别为一条直线飞行航迹段的起点和终点，在空间中两点之间的直线距离为

曲线飞行航迹段是由调整航路或航班避让以及进场盘旋等原因形成。通常，转弯可分为三种模型：内切转弯，末端转弯和约束转弯。

航路上最常使用的为内切转弯，如图2所示。其中点 p 1（x 1， y 1）为转弯初始点 与p 2 （x 2 ， y 2） 转弯结束点。

故在实际航迹的预测中，需判断得出一段航迹点中的直线段与曲线段，将相应段的航迹点进行划分，从而得到相应的直线段和曲线段拟合方程。具体航迹分段方法如下：

在典型的水平飞行航迹中，若有A，B，C三个相邻的航迹点，其中A（Xa，Ya，Za），B（Xb，Yb，Zb），C（Xc， Yc，Zc），则线段AB的直线方程为，斜率线段BC的直线方程为，斜率。故两直线间的夹角θ有P=tanθ=，则θ=arctanP。若此时θ< 10°，则A，B，C三点间用直线连接，如图3所示。若此时θ> 10°，则A，B，C三点间用曲线连接，如图4所示。

实际航迹预测过程中的分段过程如图5所示。若此时有a，b，c，d，e，f，g，h，8个航迹点。第一步首先判断a，b，c三点，经过计算可得到直线ab与直线bc间的夹角大于170°，故判断a到c点之间以直线连接；第二步，计算直线ac与直线cd之间的夹角，经计算得出，夹角小于170°，故此时的处理过程为，返回c点之前的点b，此时bd段可判断为曲线；第三步，计算直线cd与直线de之间的夹角，经计算得出，夹角小于170°，此时ce段可判断为曲线，又因为bd属于曲线段，故此时be段属于曲线部分；第四步，计算直线de与直线ef之间的夹角，经计算得出，夹角大于170°，此时e点为曲线和直线的连接点，故ef段属于直线，采用相同的方法计算直线ef和直线fg之间的夹角，直线fg，和直线gh间的夹角，得出eh段属于直线部分。此时如图5所示，将整条航迹分为了三个部分，即直线部分ab段，曲线部分be段和直线部分eh段。

图1　直线飞行航迹

图2　内切转弯示意图

图3　用直线连接

图4　用曲线连接

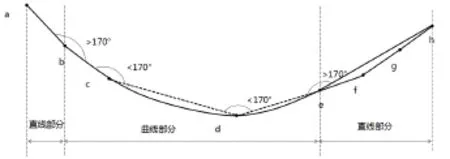
图5　航迹分段

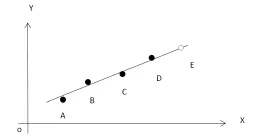
图6　直线航迹点的预测

实时航迹矢量化方法

在非实时航迹的矢量化中，可以通过对已知所有航迹点进行拟合，从而得到整条非实时的航迹；但是在实时航迹的矢量化中，仅通过预缓存的若干点进行最初阶段航迹拟合，然后对下一时间点的实时航迹位置进行预测，在得到真实的该时间点航迹位置后，又采用相应偏差纠正方法对航迹进行平滑纠正。航迹点的预测主要分为直线航迹点的预测以及曲线航迹点的预测（此处我们用椭圆方程进行曲线拟合）两类。

直线航迹点的预测

方法1：由于所预测的航迹点都是以4s为时间间隔，故在短时间内的运动皆近似为匀速运动处理。如图6所示。

其中A、B、C、D分别为时间间隔4秒的真实航迹点，E为预测的下一个航迹点。具体预测方法为：采用最小二乘法拟合得到直线方程，其中以航迹点的纬度和经度分别定义坐标轴的横纵坐标；因该段过程我们采用匀速运动处理，故（其中Xi表示i点的横坐标，i为A、B、 C、D、E），将Xe的值代入拟合得到的直线方程中，得到E点的纵坐标Ye，综上我们得到预测点E的坐标（Xe，Ye）。

曲线航迹点的预测

此处，我们采用椭圆方程对曲线进行拟合。

（1）焦点在坐标轴上

方法2：由于所预测的航迹点都是以4s为时间间隔，故在短时间内的运动皆近似为匀速运动处理。如图7所示。

这是教师针对性批改作文的做法，是“授之以渔”的一个重要方法。因为每一个学生的习作，在选材、内容、结构都不一定相同，甚至相同的题材，侧重点也不尽相同，好、中、差学生的习作也肯定不同。我们可以选择优良的习作面批面改，在全班范读，指出好在哪里，起典范作用。若为了全面提高，也要选一些其他层次的学生习作，和学生面对面地指导，教给学生修改的方法。

其中，A、B、C、D分别为时间间隔4s的真实航迹点，E为预测的下一个航迹点。又因为该椭圆的焦点分别位于X轴Y轴上，故该椭圆的方程可采用参数方程：

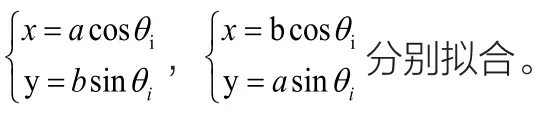
其中a，b分别为椭圆的长短半轴，θi为i点的参数（i为A、B、C、D、E点）。原点O的坐标（0，0），设A点坐标（Xa，Ya），D点坐标（Xd，Yd），E点坐标（Xe，Ye）。若向量=（Xa，Ya），=（Xd，Yd）间的夹角为ϕ，则，故将参数θe代入参数方程，即可得到E点的坐标。

（2）椭圆焦点不在坐标轴上

方法3：由于所预测的航迹点都是以4s为时间间隔，故在短时间内的运动皆近似为匀速运动处理。如图8所示。

其中，A、B、C、D分别为时间间隔4s的真实航迹点，E为预测的下一个航迹点，O'点坐标为O'（m，n）。其中，椭圆的焦点不在坐标系XOY上。虚线所表示的为原始坐标系XOY，实线所表示的是经旋转和平移后的坐标系X'O'Y'，两坐标系横轴的夹角（即旋转角）为ν。故，两坐标系之间的转化关系为

又因为该椭圆的焦点分别位于旋转平移后的X' 轴Y'轴上，故该椭圆的方程可采用参数方程

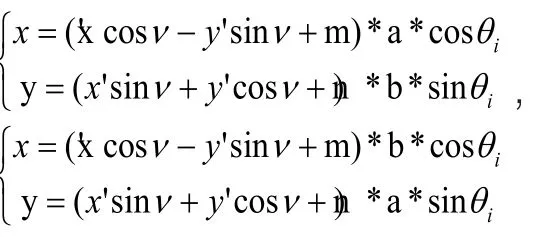
分别拟合。其中a，b分别为椭圆的长短半轴，θi为i点的参数（i为A、B、C、D、E点）。原点为O'，若向量间的夹角为ϕ，则故将参数θ代入参数方程，

e即可得到E点的坐标。

图7　焦点在坐标轴上曲线航迹点的预测

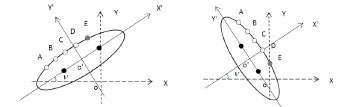
图8　焦点不在坐标轴上曲线航迹点的预测

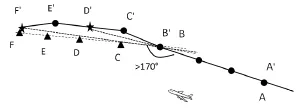
图9　直线段到直线段的过渡偏差纠正

图10　曲线段到曲线段的过渡偏差纠正

实时航迹纠正偏差方法

通过实验发现当飞机行驶方向发生偏转时，由于预测具有延迟性，预测点与真实点存在偏差，如果立即按照新预测的航迹线进行飞行，就会造成整体的航迹线在转弯处转弯角过大。为了解决上述问题，从直线段到直线段的过渡、曲线段到曲线段的过渡、直线段到曲线段的过渡及直线段到曲线段的过渡以上四种情况对航迹进行纠偏，使得经过纠偏处理后的数据拟合出的航迹更加平滑。

（1）实时航迹直线段到直线段过渡偏差修正

如图9所示，按照拟合完成的直线A'B'方程，飞机由A'点飞至B'点，将A'B'段的航迹预测看做理想状态，故此处的实际航迹AB段与预测航迹A'B'重合。在B'点之后，按照本文第三部分中所介绍的实时航迹点预测方法1，预测得到4s后的航迹点C'，但飞机经过4s后由B'点飞行至C'点，此时雷达传来真实的航迹点C点。为了将模拟航迹平滑过渡至真实航迹，采用以下方法：用C点以及该时刻向后倒推4s，8s，12s的航迹点，采用最小二乘法拟合出直线方程“f1=k1x +b1”；采用相同的方法，拟合出关于C'的直线方程“f2=k2x +b2”，当时，令当时，令所预测的下一时刻实时航迹点D'坐标，由此时所得到的直线D'B'的方程“f=kx +b”按照实时航迹点预测方法1得出。不断地迭代此过程，直至预测航迹与实际航迹接近乃至重合。故整个预测模拟航迹为点A'B'C'D'E'F'的连线。

（2）曲线段到曲线段的过渡偏差修正

如图10所示，按照拟合完成的椭圆1方“A1x2+B1xy +C1y2+D1x+E1y+F1=0”，飞机由A点飞至D点，将A'D'段的航迹预测看做理想状态，故此处的实际航迹AD段与预测航迹A'D'重合。在D'点之后，按照本文第三部分中所介绍的实时航迹点预测方法2或3，预测得到4s后的航迹点E'，但飞机经过4s后由D'点飞行至E'点，此时雷达传来真实的航迹点E点。为了将模拟航迹平滑过渡至真实航迹，采用以下方法：用E点以及该时刻向后倒推4s，8s，12s的航迹点，采用最小二乘法拟合出椭圆2方程时，令当时，令其中a=A，B，…，F 。预测的下一时刻实时航迹水平面坐标点F'由椭圆3的方程得出。不断地迭代此过程，直至预测航迹与实际航迹接近乃至重合。故整个预测模拟航迹为点A'B'C'D'E'F'G'的连线。

（3）曲线段到直线段的过渡偏差修正

如图11所示，按照拟合完成的曲线AD方程，飞机由A点飞至D点，将AD段的航迹预测看做理想状态，故此处的实际航迹AD段与预测航迹A'D'重合。在D'点之后，按照本文第三部分中所介绍的实时航迹点预测方法2或3，预测得到4s后的航迹点E'，但飞机经过4s后由D'点飞行至E'点，此时雷达传来真实的航迹点E点。为了将模拟航迹平滑过渡至真实航迹，采用以下方法：用E点以及该时刻向后倒推4s，8s，12s的航迹点，采用最小二乘法拟合出直线方程“f1=k1x +b1”；采用相同的方法，拟合出关于E'的直线方程“f2=k2x +b2”，当k1-k2＜0.1时，令k=k1，当时，令所预测的下一时刻实时航迹点F'坐标，由此时所得到的直线C'F'的方程f=kx +b按照实时航迹点预测方法1得出。不断地迭代此过程，直至预测航迹与实际航迹接近乃至重合。故整个预测模拟航迹为点A'B'C'D'E'F'G'的连线。

（4）直线段到曲线段的过渡偏差修正

如图12所示按照拟合完成的直线AC方程，飞机由A点飞至C点，将A'C'段的航迹预测看做理想状态，故此处的实际航迹AC段与预测航迹A'C'重合。在C'点之后，按照本文第三部分中所介绍的实时航迹点预测方法1，预测得到4s后的航迹点D'，但飞机经过4s后由C'点飞行至D'点，此时雷达传来真实的航迹点D点。为了将模拟航迹平滑过渡至真实航迹，采用以下方法：用E点以及该时刻向后倒推4s，8s，12s的航迹点，采用最小二乘法拟合出曲线段C'E'的椭圆方程，采用相同的方法拟合出曲线段CE的椭圆方程时，令当时，令其中a=A，B，…，F。预测的下一时刻实时航迹水平面坐标点E'由曲线段CE'（两条曲线中所夹的曲线）椭圆的方程得出。不断地迭代此过程，直至预测航迹与实际航迹接近乃至重合。故整个预测模拟航迹为点A'B'C'D'E'F'的连线。

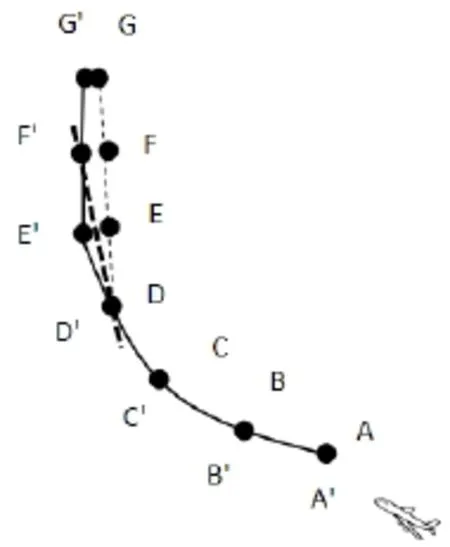
图11　曲线段到直线段的过渡偏差纠正

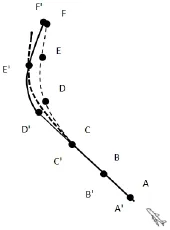
图12　直线段到曲线段的过渡偏差纠正

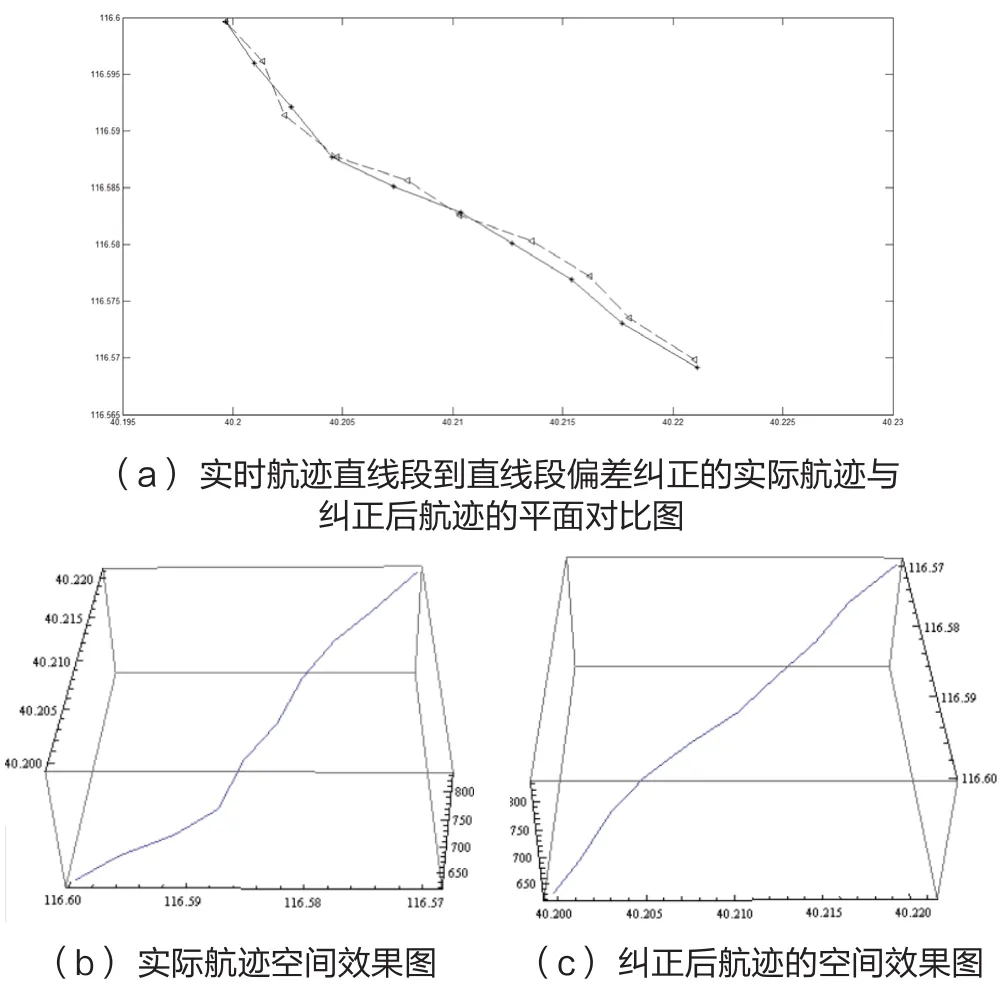
图13　实时航迹直线段到直线段的偏差纠正

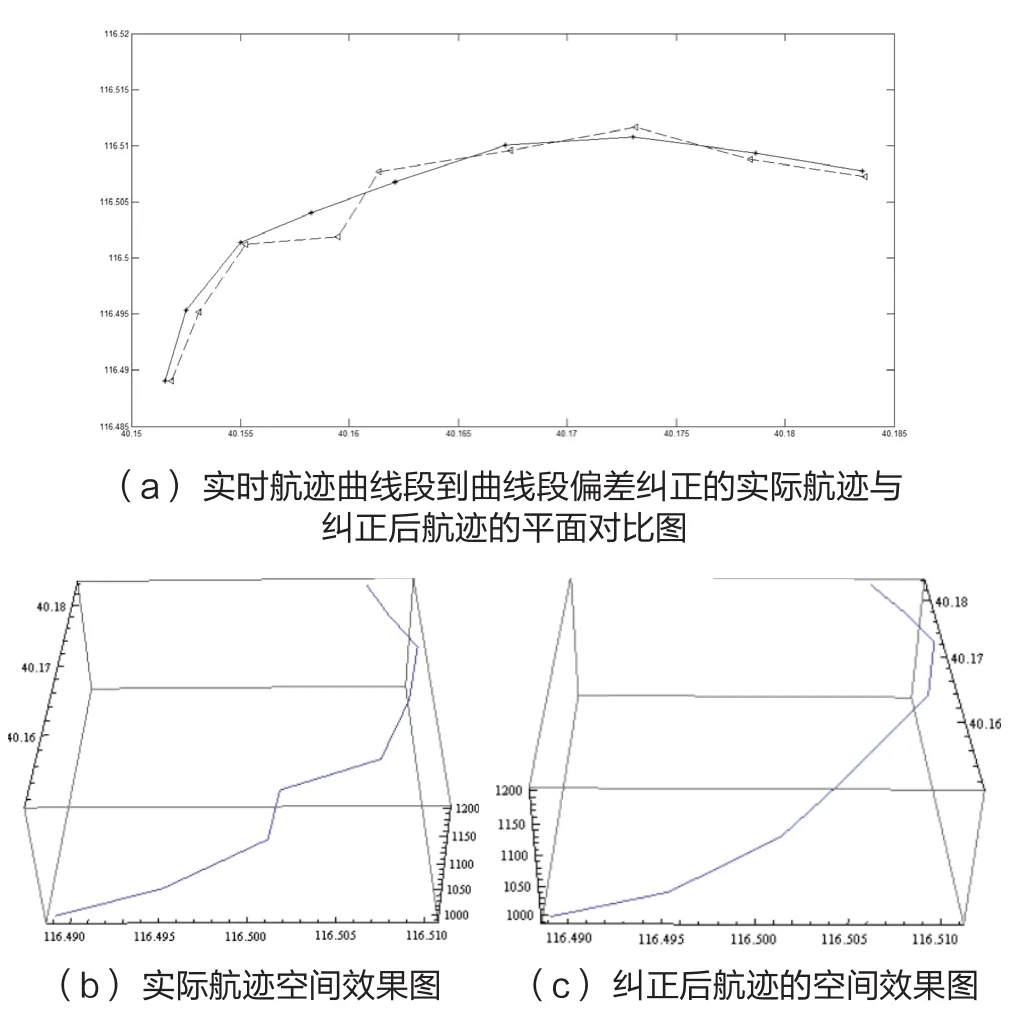
图14　实时航迹曲线段到曲线段的偏差纠正

实验验证

本实验以首都机场为例，采用首都机场提供的2013年6、7月的飞机飞行数据及机场地理位置信息，随机抽取1000条离场航迹进行实验。首先，依据实时航迹预测方法对数据进行处理预测出实时航迹，在平面坐标系内进行效果对比。利用预测出的航迹与实际航迹之间数据的剩余方差，判断预测航迹与实际航迹之间的误差，从而验证方法的有效性。

通过实验前后对比图可看出，该实时航迹预测方法预测效果较好，可满足实时航迹预测的要求。

航迹的预测精度即航迹的预测位置与实际位置之间的差值 。通过计算该预测航迹与实际航迹的稳定程度来近似估算预测方法的精度 具体来说主要步骤如下：

1）对预测航迹或实际航迹S，假设按时间顺序该航迹由点P1，...，Pm组成，对这些点的纬度x，经度y值分别做差分得到两组序列X=｛X1，...，Xm-1｝，Y=｛Y1，...，Ym-1｝，其中X1=Pi+1（x）-Pi（x），Yi=Pi+1（y）-Pi（y），通过序列X，Y把目标在x，y轴上的运动自动分解成一系列的匀速运动和匀加速运动区间U1，...，Uk；

2） 对每个区间Ui根据目标在该区间x，y 轴上的运动模型用对应的线性或二次函数对该区间的运动轨迹进行回归分析 ，得到目标在该区间的运行轨迹函数 x（t）和y（t）；

4）对航迹S上各区间的剩余方差取均值得到各航迹的剩余方差S（x2）和S（y2）；

5）对计算得到的近1000条真实航迹的剩余方差取平均值。

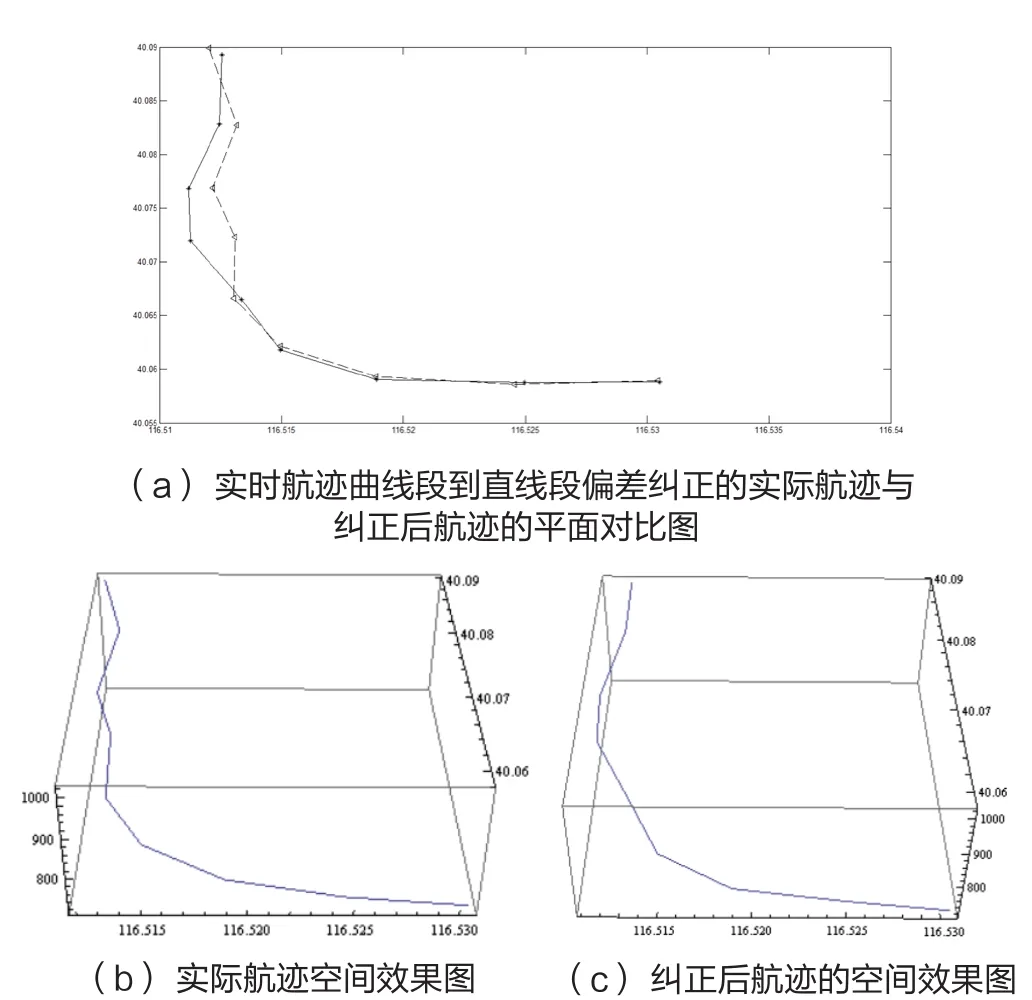
图15　实时航迹曲线段到直线段的偏差纠正

图16　实时航迹直线段到曲线段的偏差纠正

表1　435条直线段直线段航迹剩余方差的平均值

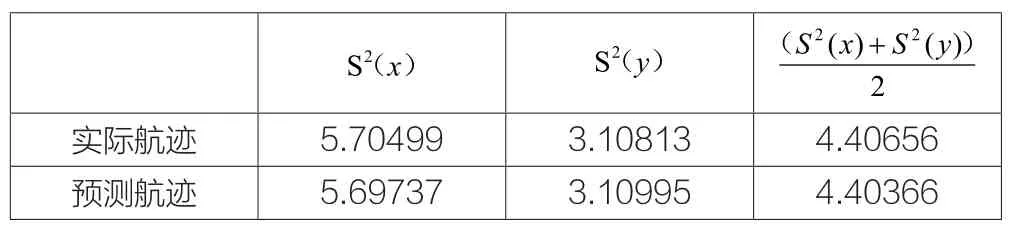
表2　386条曲线段曲线段航迹剩余方差的平均值

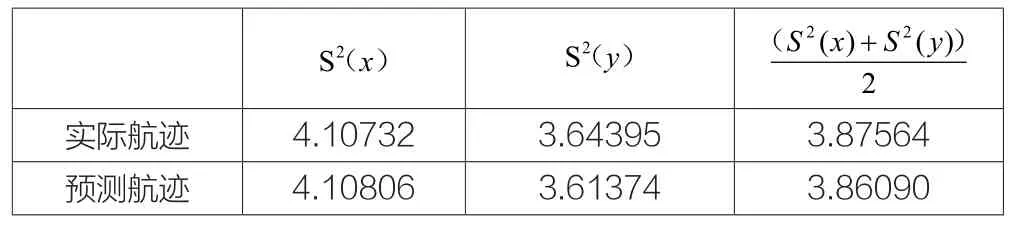
表3　236条曲线段直线段航迹剩余方差的平均值

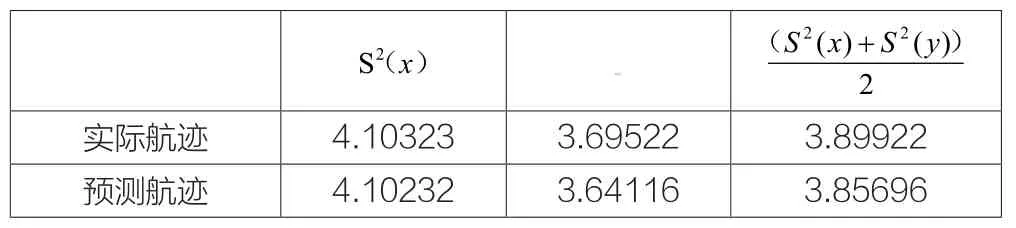
表4　215条直线段曲线段航迹剩余方差的平均值

通过实验结果得到，四种情况下实际航迹与预测航迹的最大剩余方差平均值与最小剩余方差平均值的差值为0.03211，该数量级的误差，在航迹矢量化处理后显示在雷达，将会是2至6个像素的误差，故在允许的误差范围之内。故说明该实时航迹矢量化方法是一种正确可靠，有效的实时航迹矢量化方法。

结语

本文提出了一种基于最小二乘法椭圆拟合实时航迹矢量化方法。新方法的可行性已在多次实验中得到验证。计算得到实际航迹与预测航迹的最大剩余方差平均值与最小剩余方差平均值的差值误差，实验结果理想，验证了实时航迹预测方法的有效性。新方法不仅可以解决实时航迹的矢量化问题，提供一个可行的实时航迹预测方案，还可以为场间雷达与空中雷达连接方案的制定提供有利参考。

10.3969/j.issn.1001- 8972.2016.18.021