车用轮毂电机多物理场耦合分析
王光辉, 田德文, 刘华源
(中国北方车辆研究所,北京 100072)
车用轮毂电机多物理场耦合分析
王光辉,田德文,刘华源
(中国北方车辆研究所,北京100072)
针对轮毂电机发热量大安装空间小又要满足高性能需求的问题,对轮毂电机进行多物理场耦合分析,首先在轮毂电机结构的基础上建立了电磁分析模型和电机的损耗分析模型,并通过有限元计算得到电机的损耗与效率等性能,而后结合电机温度场模型,通过结构-电磁-温度多物理场耦合模型联合仿真对电机在最大转速最大损耗下的温度场进行有限元分析计算,结果表明:电机的额定功率满足设计要求,电机内部最高温度达到103 ℃,符合绝缘及温度使用要求.
轮毂电机;有限元计算;多物理场耦合分析
为满足轮式电动车辆的性能要求,轮毂电机比常规电机应具有更高的扭矩和功率密度,但由此带来发热量大的问题,另外受制于使用环境和安装空间的约束,要求轮毂电机的安装体积要较小、防护等级要高,因此对轮毂电机的散热也提出了挑战.在轮毂电机设计过程中,要综合考虑电机的结构方案、电磁性能计算、损耗分析以及温度场分布情况,由于结构-电磁-温度等多物理场之间又相互耦合,因此对轮毂电机开展多物理场耦合分析具有重要意义.
1 轮毂电机及其电磁分析模型
针对轮毂结构约束与性能需求,平衡行星减速器与电机方案,综合匹配车辆供电体制与驱动控制要求,优化设计一种16极18槽、内转子轮毂电机,结构示意图如图1所示,表1列举了电机的主要参数.
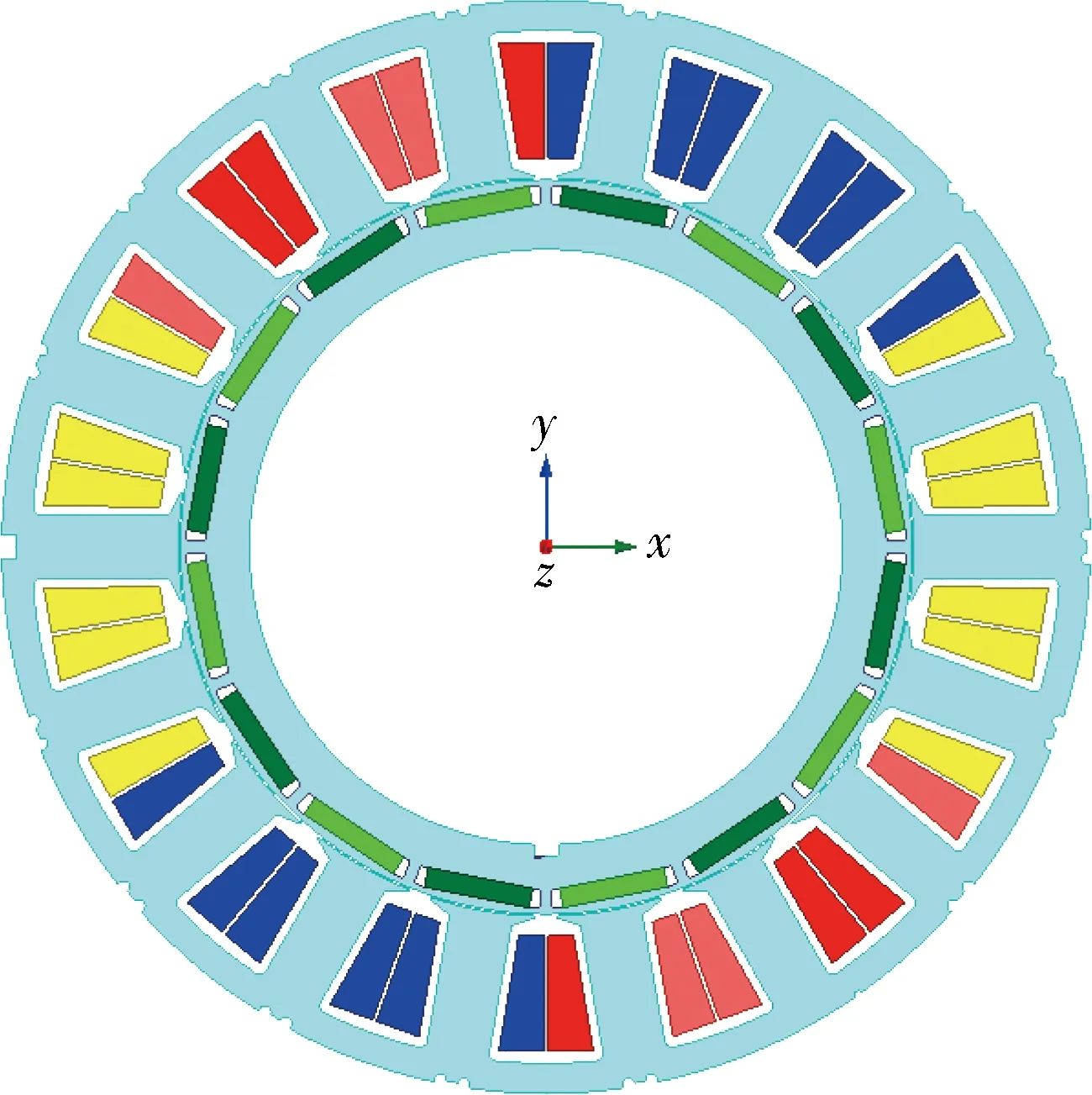
图1 轮毂电机结构示意图

电机参数参数值电机参数参数值额定功率/kW11电机槽数18额定母线电压/V320绕组连接方式Y额定转速/(r·min-1)1560定子外径/mm275最高转速/(r·min-1)4200转子内径/mm148电机极数16
不考虑位移电流的影响,电机内的电磁场属于似稳场[1].针对本研究中横截面如图1所示的电机结构,电流和磁矢位只有z轴分量,根据Maxwell方程式,该平面场域Ω上的电磁场分析问题可以表示成边值问题,如式(1)所示.
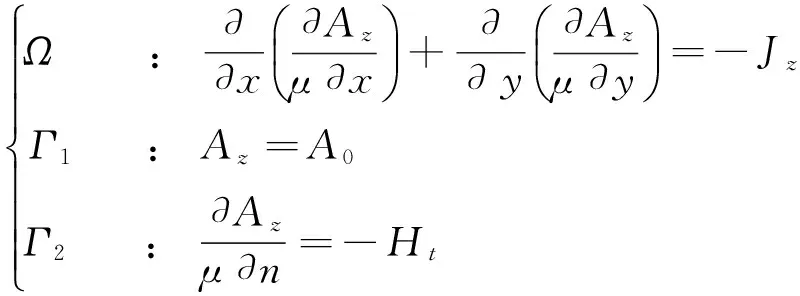
(1)
式中:μ为磁导率;Jz为电流密度;Ht为磁场强度的切向分量;Az为磁矢位的z向分量;A0为第一类边界值;Γ1、Γ2分别为第一、二类边界条件.
磁力线全部在xy平面内,磁场只有x轴和y轴方向的分量,则有
(2)
则式(1)等价为以下条件的变分问题

(3)
式中:l为第二类边界所构成的曲线.
电机的电磁场分析问题转化为根据边界条件求解式(3)中分布场磁矢位Az的解析值,然后由式(2)求解电机内部的磁感应强度B,进而分析电机的各项性能.
由于电机内边界条件复杂,直接求解式(3)是非常困难的,电磁场有限元数值计算方法以式(3)为基础,利用剖分插值方法,把式(3)的求解离散化为求解一组关于场分布的多元代数方程组问题,其能有效求解在考虑不规则边界、材料非线性、输入时变等复杂条件下的电机电磁场分布问题.电机分析模型以及计算结果如图2所示.从图2可知,其磁场分布、反电势性能以及扭矩-转速性能符合表1的设计要求.


图2 轮毂电机模型与性能计算
2 轮毂电机损耗分析
2.1轮毂电机损耗模型
2.1.1铁心损耗计算
目前按产生原理不同,通常将铁心损耗分为磁滞损耗、涡流损耗和附加损耗的分离模型[2-3],如式(4)所示.
pFe=ph+pe+pexc.
(4)
式中:pFe为铁心损耗;ph为磁滞损耗;pe为涡流损耗;pexc为附加损耗.
对于正弦分布磁场的叠片结构,采取电磁场有限元计算方法,由式(4)计算单位质量的铁心损耗,如式(5)所示.

(5)
式中:Kh为磁滞损耗系数;Ke为涡流损耗系数;Kexc为附加损耗系数.
通过对所用硅钢片的不同频率的单位质量损耗数据进行拟合,可获得它们的数值,进而赋值给材料属性,采用有限元计算方法,可计算得到电机的铁心损耗.
2.1.2绕组铜损计算
由焦耳-楞次定律知,电机运行时绕组铜线电阻的电功率损耗如式(6)所示.
pCu=3I2R.
(6)
式中:I为相电流;R为相电感.
由于轮毂电机功率密度高,工作时的电机铜耗大,因此由电机发热引起的温度升高,增加了电机绕组的阻值.电阻随绕组温度变化关系为
R=Ra[1+αa(T-Ta)].
(7)
式中:Ta为初始环境温度;Ra为温度Ta时的绕组电阻值,可通过材料属性及绕组设计直接计算得到;R为温度T时的绕组电阻值;αa为温度Ta时绕组的电阻温度系数.
2.1.3永磁体涡流损耗计算
转子上的永磁体可视为导体块,由于电机定子开槽、定子绕组电流的非正弦等因素引起的时间、空间高效谐波分量,将在永磁体内产生涡流损耗.
对永磁体区域,其磁场方程如式(8)所示.


(8)
式中:Js为电流密度;σ为材料电导率;E为电势;Hc为永磁体矫顽力.
则永磁体的涡流损耗为

(9)
对于定转子的铁心可采用硅钢片叠压降低涡流回路,从而降低涡流损耗.尽管永磁体区域的磁场变化相对铁心较小,但由于永磁体无法采用叠片结构,影响到涡流损耗,所以应该予以考虑.
2.1.4机械损耗计算
电机的机械损耗主要为风阻损耗和轴承损耗,计算公式如(10)所示.

(10)

2.2电机损耗分析与效率计算
将第1章的电磁分析模型叠加损耗模型后进行有限元分析,计算上述4种损耗,结果如图3所示.总损耗如图3(e)所示,最终根据输出性能和损耗数据,计算得到电机的效率,如图3(f)所示.可见电机在70%以上的运行区域内效率达到94%,在最大弱磁转速下最大负载时损耗最大,达到1.09 kW.

图3 轮毂电机各损耗与效率Map图
3 轮毂电机温度场模型
本研究的轮毂电机采用自然散热方式,为了保证电机能满足额定运行要求,就必须对电机的温度场进行分析.
3.1传热学模型
电机中由损耗产生的热量,其传播过程虽然十分复杂,但其散热过程一般从电机内部传导到电机表面,然后通过对流和辐射将热量散发到周围介质中.
3.1.1热传导
热传导方程是场方程,因为电机各结构之间接触面复杂,例如绕组导体和电枢铁心、永磁体和转子铁心,其中的热传导过程也很复杂.根据能量守恒原理和热传导定律,可以建立导热微分方程式(11).

(11)
式中:T为电机的温度;t为时间;ρ为材料密度;cV为质量定容热容;qV为单位体积发热率;λ为材料导热系数.
3.1.2对流传热
对流传热是指运动的流体与它所流经的固体表面之间的换热过程,满足牛顿冷却公式(12).
q=Φ/A=h(Tw-Tf).
(12)
式中:Ф为热流量,单位时间传递的热量;q为热流密度;h为表面传热系数;A为电机与流体接触面面积;Tw为电机表面温度;Tf为流体温度.
3.1.3辐射换热
电机外壳通过辐射传递能量,其发散的净热量可以通过Stefan-Boltzmann方程式(13)来计算[4].
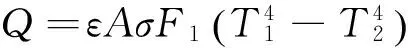
(13)
式中:ε为辐射率(黑度),大小与物体的种类及表面状态有关;σ为纯黑物体的Stefan-Boltzmann常数(5.7×10-8W/m2·K);A为辐射面的面积;F1为电机辐射面的形状系数;T1为电机辐射面的绝对温度;T2为电机外部辐射接触面的绝对温度.
3.2温度场计算模型
考虑到轮毂电机使用环境,将减速器、轮辋外侧面一同考虑进去,真实工况十分复杂,本研究仅针对其中的主要因素,建立如图4所示的自然冷却条件下的轮毂电机温度场计算模型.
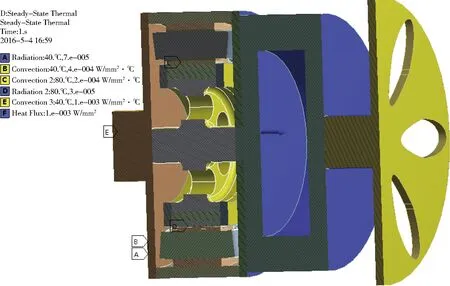
图4 轮毂电机温度场计算模型(半剖视图)
在图4所示的温度场计算模型中,轮毂电机在40 ℃环境温度下通过以下3个方式散热:1)外表面辐射散热(条件A);2)行驶中电机端盖左侧面和轮辋右侧面对流散热(条件B);3)与车体连接部位的传导散热(条件E).同时电机转子在80 ℃内部温度下通过以下2个方式散热:1)外表面辐射散热(条件D)2)高速旋转过程中空气对流传热(条件C).
另外减速器在工作时也将产生热量,减速器效率在99%左右,估计产生损耗110 W,温度场计算模型中对减速器模拟内腔体表面施加110 W的热源.整个模型只考虑车辆连续行驶,电机在最大车速电机额定功率下,不考虑减速过程中制动盘的发热.
4 联合仿真分析
电机结构、电磁场、温度场等多个物理场是相互制衡、相互影响具有一定耦合关系的综合物理场,对于电机内部多物理场的耦合数值计算具有非常现实的意义和应用价值.本研究针对上述问题建立如图5所示的结构-电磁-温度联合仿真分析模型.

图5 轮毂电机结构-电磁-温度联合仿真分析模型
首先将电机模型A导入到结构分析模型C中,而后将第1章中电磁场分析模型B的电磁扭矩分析结果导入到结构分析模型C中,其中电磁扭矩导入结果如图6(a)所示.同时对转子施加4 200 r/min的最高转速,作为负荷条件.
通过结构仿真分析计算,可得电机转子的结构变形量如图6(b)所示.最大变形量只有2.5 μm,因此电机内嵌式结构符合设计要求,转子在最大转速旋转时不会与定子摩擦.
而后将电机模型从结构分析模型(C)导入到温度场(稳态热)分析模型(D)中,同时将电磁场分析模型(B)的损耗分析结果导入到温度场分析模型(D)中,对电机的内部温度分布进行分析计算,结果如图7所示.从图7中可知,电机的转子温度高于定子温度,最高温度达到103 ℃.仿真结果表明,设计符合绝缘及温度使用要求.

图6 结构-电磁耦合模型及仿真分析结果

图7 稳态温度场分析结果(半剖视图)
5 结 论
本研究在轮毂电机结构模型、电磁计算以及损耗分析的基础上结合电机温度场模型,通过结构-电磁-温度多物理场耦合模型联合仿真,结果表明,最高温度符合绝缘及温度使用要求,电机方案满足性能要求.本研究所述方法适用于在项目前期设计轮毂电机方案,以指导电机的工程设计,但应当指出,在实际轮毂电机加工制造过程中,由于原材料、加工精度、制作工艺等影响,上述分析必然带有误差,后续待所设计电机加工完成后,结合实际试验测试结果,再对模型不断进行完善,以提高模型的准确性,为后续轮毂电机进一步优化设计提供指导.
[1]唐任远,等. 现代永磁电机理论与设计[M]. 北京:机械工业出版社,2006.
[2]G.Bertotti, A.Bogelietti, M.Chiampi. An Improved Estimation of Iron Losses in Rotating Electical Machines[J].IEEE Transaction on Magnetics. 1991, 27(11):5007-5009.
[3]Chunting Mi, Gorden R.Selmon, Richard Bonert. Modeling of Iron Losses of Permanent-magnet Synchronous Motors[J]. IEEE Transactions on Industry Applications. 2003, 29(6):734-741.
[4]T.J.E Miller. Speed’s Electric Machines with Problems and Solutions[M].SPEED Software Manual,2014.
Multi-Physics Coupling Analysis of in-Wheel Motor
WANG Guang-hui,TIAN De-wen,LIU Hua-yuan
(China North Vehicle Research Institute, Beijing 100072,China)
To mediate the contradiction between small installation spaces, large heat generation of in-wheel motor and its high performance requirements, it is very necessary to analyse the motor performance considering the multi-physics coupling phenomenon. Firstly, the model for structure with electromagnetic simulation and loss calculation is established, through which the performance of motor loss and efficiency, etc. are analyzed by finite element method. Then combined with the steady-state thermal model, the temperature distribution under the condition of maximum speed and maximum loss is deduced considering coupling of structure-electromagnetic-thermal physics. Finally, the result shows that the in-wheel motor performance meets its requirements and its maximum temperature is 103℃ that is below the insulation grade and motor usage temperature.
in-wheel motor;finite element analysis;multi-physics coupling analysis
1009-4687(2016)03-0027-06
2016-07-14.
王光辉(1987-),男,高级工程师,主要研究方向为电机设计、驱动控制、人工智能与优化计算.
TH137.51
A

