Volterra型积分微分动力系统的稳定性
王春生
(广州大学华软软件学院 管理系,广东 广州 510990)
Volterra型积分微分动力系统的稳定性
王春生
(广州大学华软软件学院管理系,广东广州510990)
采用Banach不动点方法研究一类Volterra型积分微分动力系统零解的指数渐近稳定性,得出该系统零解指数渐近稳定性定理,并对该定理给出严格证明.结论改进了相关文献的结果.
Banach不动点方法;Volterra型积分微分动力系统;指数渐近稳定性.
很多专家学者都利用Lyapunov法研究过确定型和随机微分方程周期解的存在性、有界性和零解的稳定性.然而,一百多年来,人们在利用此方法时遇到了一些困难,如在研究变时滞微分方程的稳定性时,Lyapunov条件往往要求时滞有界等.近年来,Burton及其合作者第一次尝试应用不动点方法研究了确定性微分方程周期解的存在性、有界性和零解的稳定性[1-6],一定程度上克服了上述出现的困难,得到了很好的结论.最后,Burton在文献[6]中采用Lyapunov方法和不动点方法研究同一种微分动力系统,得出了使得该系统零解稳定的两个结论,文章最后还对两个结果进行了分析比较,得出不动点方法在一定程度上较Lyapunov方法优越,如不动点方法得出的结论不需要时滞有界等.作为不动点方法的推广,文献[7-10]中利用不动点方法研究了随机积分微分、中立型随机积分微分和中立型多变时滞随机动力系统零解的稳定性.本文将继续采用Banach不动点方法研究一类非卷积型线性Volterra积分微分方程的指数渐近稳定性.
1 一类非卷积型线性Volterra积分微分动力系统
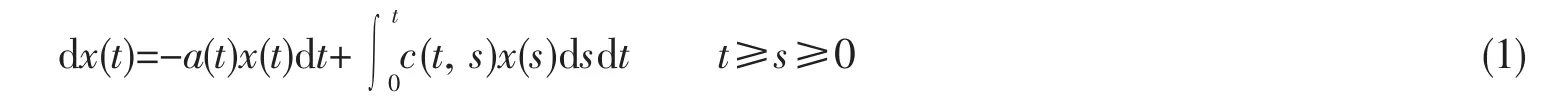
初始条件x0=ξ.其中,a(t)∈C(+,),c(t,s)∈C(+×+,).
2 主要结果
定义1如果存在λ>0和任意的ε>0,都存在δ=δ(ε)使得当,则称系统(1)零解指数渐近稳定.
Tadayuki Hara在文献[11]中利用Lyapunov方法研究了系统(1)零解的指数渐近稳定性,得到定理1.
定理1假设存在正常数μ使得
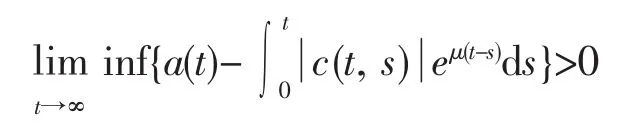
则系统(1)的零解指数渐近稳定.
本文将采用Banach方法研究系统(1)零解的指数渐近稳定性,得到如下结论:
定理2假设存在正的常数M,M0,γ,κ,β和η∈(0,1)以及连续函数h(s):[0,∞]→,使得对t≥0,
设算子Ψ:S→S:
1)(Ψφ)(0)=ξ;
易证,Ψ是连续的.下面将说明Ψ(S)⊂S.即当t→∞时,.因为,由条件(ii),易证当t→∞时,
此外,由条件(ii)知,
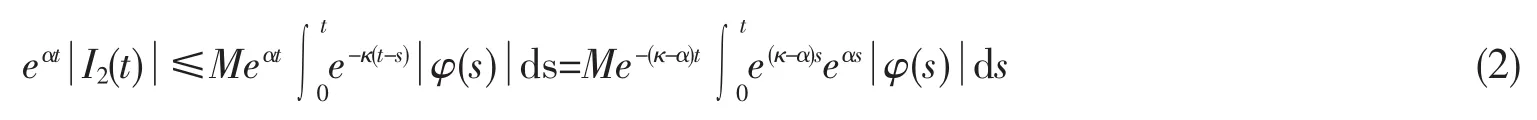
对任意φ(t)∈S和ε>0,存在t1>0使得当s≥t1时,.所以由式(2)得
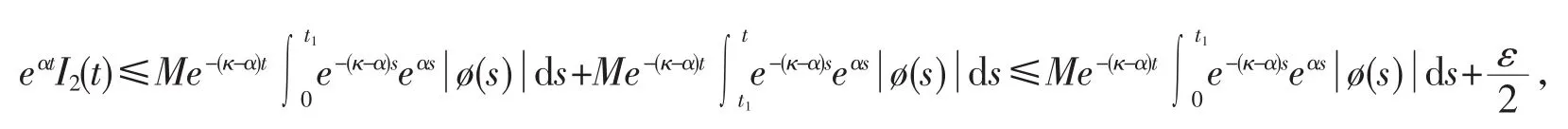
由于当t→∞时,e-(κ-α)t→0.所以存在t2≥t1使得对任意的s≥t2都有,当t→∞时,
再者,有条件(iii)知,
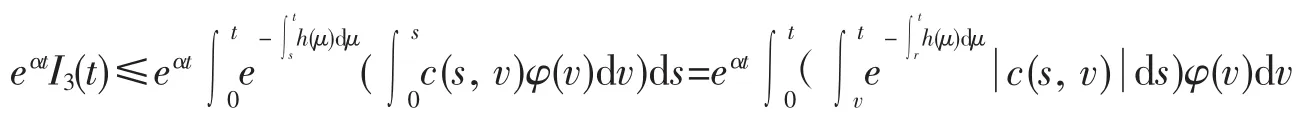
最后,证明Ψ是压缩的,由条件(iv)易知,对任意φ,ξ∈S有
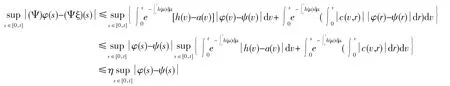
所以,Ψ是压缩映射.由压缩映射定理知,Ψ在空间S上存在唯一不动点x(t).满足x(0)=ξ,且存在满足0<α<min{κ,γ,β}的正常数α,使得当t→∞时,.所以系统(1)的零解指数渐近稳定.故得证.
3 实例
前面在研究系统(1)稳定性时,本文通过选取合适的h(s),一定程度上改进文献[11]的结论.下面将以实例说明在某些情况下,本文的结论即定理2优于文献[11].
例考虑如下非卷积型线性Volterra积分微分动力系统
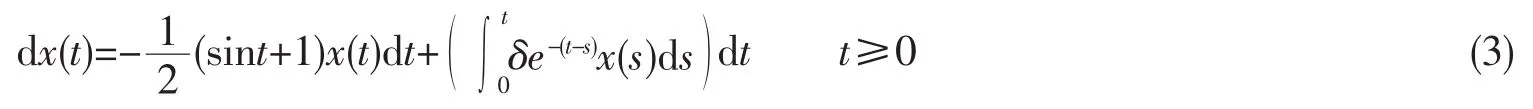
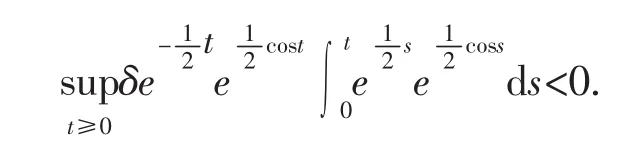
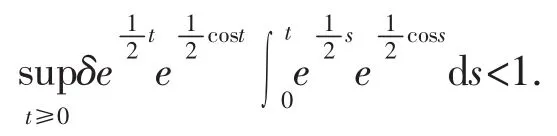
但是在文献[11]的结论中,找不到满足条件的μ>0,使得
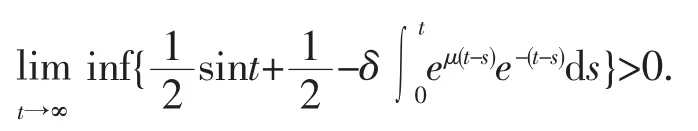
所以,由文献[11]得不出系统(3)零解的指数渐近稳定性.
3 结论
1)文章利用Banach不动点定理研究了一类非卷积型Volterra积分微分动力系统零解的指数渐近稳定性,所得结论改进了文献[11]的结果.
2)不动点方法通过引入合适的h(s)函数构造算子,并判断模型稳定性,使得系统稳定性研究简单易行.
总之,本文利用Banach不动点方法讨论一类非卷积型Volterra积分微分动力系统零解的指数渐近稳定性,有其特定优越性.
[1]BURTON T A.Fixed points and stability of a non-convolution equation[J].Proceedings of the American Mathematical Society,2004,132(2): 3679-3687.
[2]BURTON T A,FURUMOCHI T.A note on stability by Schauder’s theorem[J].Funkcialaj Ekvacioj,2001,44(1):73-82.
[3]BURTON T A,FURUMOCHI T.Fixed points and problems in stability theory for ordinary and functional differential equations[J].Dynamical Systems&Applications,2001,10(1):89-116.
[4]BURTON T A,FURUMOCHI T.Krasnoselskii’s fixed point theorem and stability[J].Nonlinear Analysis Theory Methods&Applications,2002,49(4):445-454.
[5]RAFFOUL Y N.Stability in neutral nonlinear differential equations with functional delays using fixed point theory[J].Mathematical&Computer Modelling,2004,40(7-8):691-700.
[6]BURTON T A.Stability by fixed point theory or Liapunov’s theory:a comparison[J].International Journal on Fixed Point Theory Computation& Applications,2003,1(1):15-32.
[7]王春生,李永明.中立型多变时滞随机微分方程的稳定性[J].山东大学学报:理学版,2015,50(5):82-87.
[8]王春生,莫迟.不动点与一类随机积分微分方程的稳定性(英文)[J].广州大学学报:自然科学版,2009(2):49-53.
[9]王春生.中立型随机积分微分方程的稳定性[J].四川理工学院学报:自然科学版,2011,24(1):81-84.
[10]王春生.随机微分方程稳定性的两种不动点方法的比较[J].四川理工学院学报:自然科学版,2012,25(4):81-84.
[11]APPLEBY JHON A D.Exponential asymptotic stability for Volterra integrodifferential equations of nonconvolution type[J].Funkcialaj Ekvacioj,1994,37(2):373-382.
Stability of Volterra Integro-differential Dynamic System
WANG Chunsheng
(School of Management,South China Institute of Software Engineering,Guangzhou University,Guangzhou 510990,China)
In this paper,the exponential asymptotic stability for a kind of Volterra integro-differential dynamic system zerosolution has been studied by using the method of Banach fixed point,with drawing the conclusion of zero solution exponential asymptotic stability for this system.At the same time,the strict evidence has been given in this article for the achieved stability.The conclusion has improved the results of relative articles,with the detailed example in the following.
Banach fixed point method;Volterra integro-differential dynamic system;Exponential asymptotic stability.
O231.1
A
2095-4476(2016)08-0005-03
2016-07-07;
2016-08-10
广东省自然科学基金资助项目(2016A030313542);广东省普通高校青年创新人才项目(自然科学)资助项目(2015KQNCX200);广州大学华软软件学院教学、科学研究项目资助项目(ky201402)
王春生(1982—),男,安徽桐城人,广州大学华软软件学院管理系讲师.
(责任编辑:饶超)

