石墨烯纳米条带的热电性质研究
潘长宁,何 军,钟春良
(湖南工业大学 理学院,湖南 株洲 412007)
石墨烯纳米条带的热电性质研究
潘长宁,何军,钟春良
(湖南工业大学 理学院,湖南 株洲 412007)
利用非平衡格林函数方法与朗道输运理论,研究石墨烯纳米条带的热电性质。研究结果表明:zigzag型石墨烯纳米条带的热电性质随着宽度的增加而减少;armchair型石墨烯纳米条带的热电性质不仅与宽度有关,而且与其带隙是否被打开有关,当其表现为半导体时,其热电性质远大于zigzag边缘的石墨烯纳米条带。
石墨烯纳米条带;声子热导;热电性质
0 引言
随着科学技术不断进步,电子器件逐步实现小型化、高度集成化的同时,其芯片热功率密度也以指数形式迅速增长[1],局部温度过高会影响器件工作的稳定性和使用寿命。如何将产生的热量转移和排出成为纳米器件发展迫切需要解决的问题;与此同时,随着全球工业化进程的加快,能源消耗日益增加,过度开采使石化燃料等传统能源日趋枯竭,废热肆意排放使生态平衡遭到严重破坏。为了有效地利用能源和最大程度地保护环境,科学家们做出了很多的努力。目前,一个非常可行的办法就是寻找高性能的热电材料和器件,将工作时产生的“废热”直接转换为电能并合理地加以利用。通常情况下,材料的热电转换性能可以用热电优值来描述[2-3],即

式中:T为系统的绝对温度;Ge为电子电导;S为Seebeck系数;ph为声子热导;e为电子热导。
ZT值越高意味着材料具有更高的热电转换性能。由于决定材料热电性能的物理量之间内部存在相互联系、相互制约的关系,其中一个量的改变会导致另一个量的变化,因此提高材料的ZT值受到很大的限制。
在以往体材料研究中,基于碲的化合物(如碲化铋、碲化铅、碲化锗等)都是研究的热点,并取得了很大的进展。自从L. D. Hicks等[4]提出通过量子受限效应方法来提高材料的ZT以后,研究者对低维物理和纳米结构的热电性质非常关注,并进行了广泛的研究,试图通过低维纳米结构本身的输运特点(如量子受限、载流子能量过滤、声子边界散射等)来提高其热电性能,其中最为典型的就是石墨烯纳米带结构[5-8]。因此,本文拟对不同手性的石墨烯纳米条带的声子、电子的输运性质以及热电性能进行对比研究,以期得到一些有意义的结果。
1 石墨烯纳米条带模型
根据边界结构不同,石墨烯纳米带可分为边界呈锯齿型的锯齿型石墨烯和边界呈扶手椅状的扶手椅型石墨烯。如图1为zigzag型(锯齿型)和armchair型(扶手椅型)石墨烯纳米条带模型图。zigzag型石墨烯纳米条带简称ZGNRs(zigzag-edge ribbons),armchair型石墨烯纳米条带简称AGNRs(armchair-edge ribbons)。本文中,Nz-ZGNR和Na-AGNR表示不同宽度的石墨烯纳米条带,其中Nz和Na为正整数。

图1 石墨烯纳米条带模型图Fig. 1 The model diagram of GNRs
通过非平衡格林函数计算模拟,可以计算声子的透射系数Tph和电子的透射系数Te。在计算声子的输运时,采用包含四近邻的力常数模型[2-3];在计算电子的输运时,其哈密顿量用最近邻的紧束缚原子模型模拟[2-3]。由于声子与声子、电子与声子相互作用比较弱,可以忽略声子-声子、电子-声子的相互作用,而只考虑声子与电子的弹性传输,其电子的透射系数可以表示为
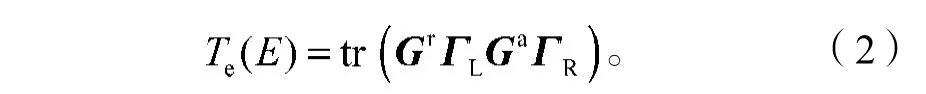
式中:E为电子能量;tr为对矩阵求迹;Ga为量子点中心散射区的前进格林函数;Gr=(Ga)÷表示中心散射区的推迟格林函数,它们互为共轭;,分别为中心散射区域与左、右端半无限长区域库函数的耦合。
在计算得到透射系数后,就可以求解与热电因子ZT有关的各项物理量。为了描述的方便,引入中间函数,即

那么各电学量可简便地表示为:

式(4)~(5)中e为电子的电量。
采用类似方法可以计算声子的输运性质。具体的过程如下:在上面的计算步骤中,用声子的力常数矩阵K代替电子的哈密顿量He;用声子的频率代替电子的能量,即,其中,为声子的频率,为很小的正数。通过以上的运算,就可以方便地计算出声子的透射系数,从而计算出声子热导,即

2 数值结果和讨论
由于电子的传输性质对材料的热电性质影响非常大,因此分析电子的能带结构非常重要,图2为ZGNRs的能带随宽度的变化关系。从图中可知,ZGNRs的最高价带与最低导带总是在波矢k=时能级简并,且几乎平行于费米能级。在费米能级附近,ZGNRs电子的态密度呈现出奇异的峰值,这是因为其拥有高度极化的边缘态,因此所有的ZGNRs均表现为金属性,如Nz=4, 6, 8等。图3为AGNRs的能带随宽度的变化关系。从图中可知,AGNRs的电子性质依赖于它们的宽度:当宽度满足Na=3n+2时,其中n是整数,纳米条带Na-AGNR表现为金属性;否则,其带隙将被打开,呈现为半导体性质,如Na=7, 9时,其带隙被打开,而且9-AGNR的带隙明显小于7-AGNR,而8-AGNR仍然表现为金属性。

图2 ZGNRs的色散关系Fig. 2 The energy dispersion of the ZGNRs

图3 AGNRs的色散关系Fig. 3 The energy dispersion of the AGNRs
图4描绘了纳米带的电导随化学势的变化情况。

图4 石墨烯纳米带的电导Fig. 4 The electronic conductance of GNRs
从图4中可以看出,石墨烯纳米带的电导都呈阶梯型变化,即为量子化电导G0=2e2/h=77.4S的整数倍,且随着化学势的增加而增加。这是因为,电子的透射通道随着化学势的增加而被打通,更多的通道导致电子透射增加,电导随之增加,且最高电导随着纳米条带的增加而增大。对比图4b中的曲线可知,纳米带7-AGNR和9-AGNR的电导在中心对称点附近几乎为0。这是因为,石墨烯的带隙由于裁剪而被打开,在导带和价带间形成了禁带,很少有电子发生透射而导致Ge=0。随着宽度的增加带隙明显减小,如7-AGNR的带隙宽度为1.4 eV,9-AGNR的带隙宽度为1.0 eV。当宽度继续增加,一维的纳米条带变为二维的石墨烯时,其带隙也将随之消失。
图5为石墨烯纳米条带Seebeck系数随化学势的变化情况。
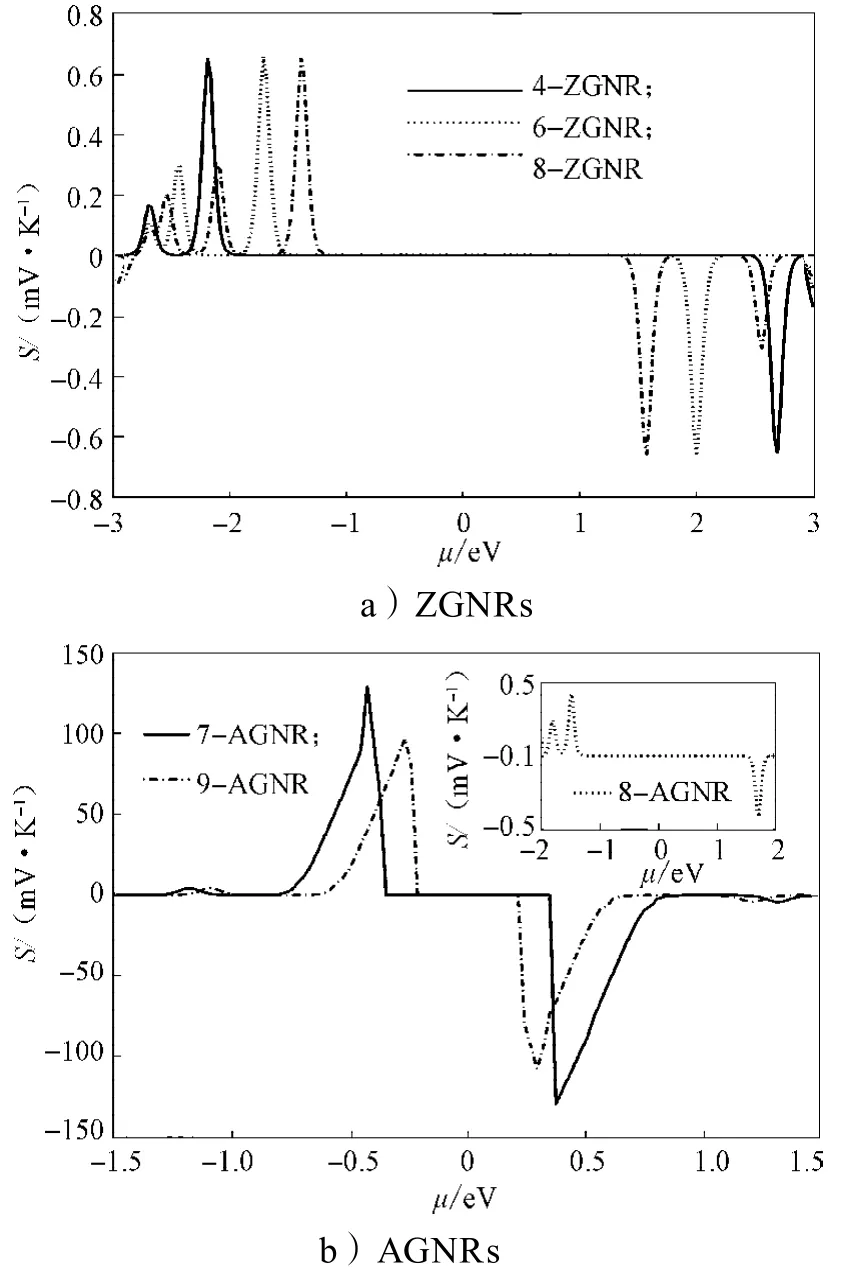
图5 石墨烯纳米带的Seebeck系数Fig. 5 The Seebeck coefficient of GNRs
由图5可知,Seebeck系数关于中心对称点呈反对称结构,这可以从式(5)得到合理的解释。因为能谱的子带是对称的,而L(1)是能量E-的奇函数,电子的透射则为偶函数,因而出现反对称的Seebeck图。根据Seebeck系数的定义,它的大小取决于能量为E-的电子透射权重平均值。在导带边缘,电子具有更高的E-而对Seebeck系数的贡献较大,尤其是第一导带边缘的电子。因此,石墨烯纳米条带的Seebeck系数的峰值出现在费米能附近和第一导带边缘。当带隙被打开,Seebeck系数呈指数倍增大。例如,4-ZGNR的Seebeck系数在第一导带边缘(化学势=2.2 eV附近)达到最大值0.65 mV/K,远小于半导体性armchair边缘的7-AGNR,S=130 mV/K。对于具有相同手性的AGNRs,金属性的纳米条带8-AGNR的Seebeck系数(如图5b所示)也很低,其S=0.42mV/K。
图6描述了室温下(T=300 K)热电优值ZT随化学势的变化。

图6 石墨烯纳米带的热电优值ZT(T=300 K)Fig. 6 The thermoelectric merit of GNRs ZT(T=300 K)
由图可以看出,纳米条的ZT出现了一系列的峰值,这些峰值都在子带的边缘。而且随着宽度的增加呈减小的趋势。纳米带4-ZGNR的最大优值ZT= 0.073,稍大于6-ZGNR的ZT=0.058。而由于带隙的存在,半导体7-AGNR和9-AGNR有相对较高的热电优值,例如7-AGNR的ZT=0.190,比ZGNRs的热电优值高出几倍。此外,金属性AGNRs的热电性能也很低,例如,8-AGNR的ZT值低于0.03。因此,带隙的打开有利于提高系统的热电性能。
3 结语
利用非平衡格林函数方法和朗道输运理论相结合,研究了石墨烯纳米带的热电性质。通过研究发现,带隙的打开有利于增大系统的热电动势、提高热电性能。这一研究结果对未来纳米热电装置的设计有一定的参考价值。
[1]POP E,SINHA S,GOODSON K E. Heat Generation and Transport in Nanometer-Scale Transistors[J]. Proceedings of the IEEE,2006,94(8):1587-1601.
[2] PAN C N,XIE Z X,TANG L M,et al. Ballistic Thermoelectric Properties in Graphene-Nanoribbon-Based Heterojunctions[J]. Applied Physics Letters,2012,101(10):103115-1-103115-4.
[3]XIE Z X,TANG L M,PAN C N,et al. Enhancement of Thermoelectric Properties in Graphene Nanoribbons Modulated with Stub Structures[J]. Applied Physics Letters,2012,100(7):073105-1-073105-4.
[4]HICKS L D,DRESSELHAUS M S. Effect of Quantum-Well Structures on the Thermoelectric Figure of Merit[J]. Physical Review B,1993,47(19):12727-12731.
[5]GUNST T,MARKUSSEN T,JAUHO A P,et al. Thermoelectric Properties of Finite Graphene Antidot Lattices[J]. Physical Review B,2011,84(15):667-673.
[6]OUYANG Y,GUO J. A Theoretical Study on Thermoelectric Properties of Graphene Nanoribbons[J]. Applied Physics Letters,2009,94(26):263107-1-263107-3.
[7]YANG K K,CHEN Y P,Dagosta R,et al. Enhanced Thermoelectric Properties in Hybrid Graphene/Boron Nitride Nanoribbons[J]. Physical Review B Condensed Matter,2012,86(4):3701-3704.
[8]MAZZAMUTO F,NGUYEN V H,APERTET Y,et al. Enhanced Thermoelectric Properties in Graphene Nanoribbons by Resonant Tunneling of Electrons[J]. Physical Review B,2011,83(23):1417-1425.
(责任编辑:申剑)
Study on Thermoelectric Properties of Graphene Nanoribbons
PAN Changning,HE Jun,ZHONG Chunliang
(School of Science,Hunan University of Technology,Zhuzhou Hunan 412007,China)
Investigated the thermoelectric properties (TE) of graphene nanoribbons (GNRs) by method of nonequilibrium Green's function approach and Landauer transport theory. The results show that TE of zigzag type GNRs decreases with its width increasing, TE of armchair edge GNRs are not only related to its width, but also with the band gap open or not, when it appears as a semiconductor, its thermoelectric properties are much larger than that of zigzag edge graphene nanoribbons.
graphene nanoribbon;phonon thermal conductivity;thermoelectric property
O482.4
A
1673-9833(2016)02-0068-04
10.3969/j.issn.1673-9833.2016.02.013
2016-01-05
国家自然科学基金资助项目(11374094),湖南省自然科学基金资助项目(2015JJ2050,2015JJ3060)
潘长宁(1976-),男,湖南新化人,湖南工业大学副教授,博士,主要从事低维物理中的电子和声子输运方面的研究和教学,E-mail:panchangning2000@sina.com

