药品包衣厚度测量系统晶振频率分析及实验研究

何高法，周传德，任建兵，马　霞

（重庆科技学院机械与动力工程学院，重庆 401331）

药品包衣厚度测量系统晶振频率分析及实验研究

何高法，周传德，任建兵，马霞

（重庆科技学院机械与动力工程学院，重庆 401331）

为提高药品包衣效果和包衣质量，针对包衣厚度在线监测问题，提出基于石英晶体谐振原理的包衣厚度测量方法。利用石英晶体的压电效应原理分析石英晶体谐振片厚度剪切振动的谐振频率与包衣厚度之间的函数关系，使用等效密度法建立有限元模型并分析石英晶体谐振器在不同膜厚情况下的模态和谐振频率，理论和有限元分析结果均表明晶片的谐振频率随薄膜厚度的增加而降低，且呈近似的线性关系，检测灵敏度约为12kHz/μm。使用石英晶体微天平系统进行包衣厚度的测量实验，实测厚度和分析结果具有很好的一致性。研究结果表明基于石英晶体谐振的膜厚测量法可以应用于制药包衣厚度的实时测量。

石英晶体谐振器；薄膜厚度；包衣；有限元分析

0　引　言

薄膜包衣技术是将包衣液（聚合物溶液或混悬液）通过喷头雾化后与悬浮的颗粒接触碰撞，在颗粒表面形成薄膜层（厚度5～50 μm），是目前制药行业广泛应用的技术之一。包衣的厚度及其均匀性是影响药品质量、疗效以及制药成本的一项重要指标，所以也是评价包衣效果和包衣机质量的重要指标。

目前，对包衣厚度的测量方法主要有直接测量法和间接测量法。直接测量法根据测量原理的不同，又可以分为显微图像测量法［1］、近红外光谱法［2］、拉曼光谱法［3］、X射线荧光光谱法［4］以及太赫兹光谱方法［5］等，上述各方法均是将产品制样后直接测量包衣厚度，准确性较高。

生产中普遍采用的间接测量方法为称重法，即先测出包衣前素芯的整体质量，然后再测量出包衣后药品的总质量，最后根据包衣质量和所有药片的表面积计算包衣厚度。这种方法较为简单，但是测量误差较大。

上述所有测量方法均为包衣完成后的测量，不能对包衣厚度进行实时测量和控制，而对包衣厚度进行实时准确测量是提高包衣质量的有效方法，特别在药品试制和研发阶段。

基于石英晶体振荡技术的薄膜厚度测量方法是用于离子镀膜机等薄膜制备工艺中的膜厚控制方法之一，为了将这一方法引入制药包衣厚度测量和控制中，本文从理论上研究其可行性并进行了实验验证。

1　石英晶体谐振测厚原理及频率变化理论分析

石英晶体谐振器由AT切石英晶片和在晶片上下表面制作的两个电极构成。测量时，当电极上附着物质量（或厚度）改变时，晶振片的谐振频率将随之改变，通过测量频率的变化率来表征附着物厚度的变化。

AT切圆形平片型石英晶片在电场激励下，其各种正常模的本征频率［6］为

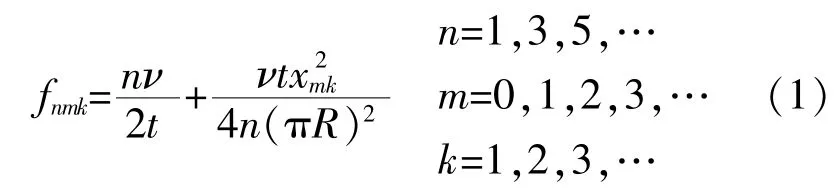
式中：ν——波在晶片平面上的传播速度；

t——石英晶片的厚度；

R——晶片表面电极半径；

xmk——m阶贝塞尔函数的k次根。

当电极半径远大于晶片厚度时（R＞＞t），则式（1）可以写为

式中：K——石英晶体的频率常数，Hz·m；

cij——石英晶体弹性系数；

ρ——石英晶体密度。

对于AT切割的石英晶体片，K的值为1654Hz·m。选用普通石英晶振片，其电极直径为6 mm，电极厚度为0.272mm；则由式（2）可以计算得出谐振片的基频约为6.08093MHz。

对式（2）微分得﹕

式（3）表明：若厚度为t的石英晶体增加厚度Δt，则晶体的振动频率变化了Δf，式中的负号表示晶体的频率随着厚度的增加而降低。

使用石英晶振片测量薄膜厚度时，将附着在晶片上的膜材厚度转换为石英晶体的厚度，两者厚度之间的关系可以表示为

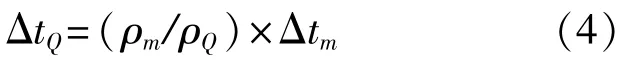
式中：ΔtQ——石英晶体厚度增量；

Δtm——膜层厚度增量；

ρm——膜层的密度；

ρQ——石英晶体的密度。

将式（4）代入式（3）中，则有﹕

对于某一种确定的包衣材料，ρm为常数，式（5）表明：当包衣膜厚远小于石英晶振片厚度时，石英晶体频率的变化量Δf与包衣厚度变化量Δtm为线性关系。

2　晶片厚度剪切振动模态的有限元分析

在对晶体谐振器进行设计和分析时，需要考虑电极几何参数和晶片几何参数等对晶片谐振频率的影响。这些参数包括电极形状、位置、尺寸和晶片的形状、几何尺寸等。另外，还需要分析晶片夹具设计和周围介质等对晶片谐振频率的影响等。这就需要对晶片进行机电以及多物理场的耦合分析，而目前理论研究大多利用解析和半解析的方法将问题近似为一维或二维模型，对材料常数作近似处理，进行简单的近似分析。为了验证晶振片可以用于包衣厚度测量系统中，需要对晶振片的模态和频率进行准确分析，有限元法为这一分析提供了有效手段［7-9］。

2.1建立几何模型的等效密度法

在建立有限元模型时，由于电极层厚度（100nm）与晶片厚度（0.272mm）相比很薄，若对其直接建模，有限元的单元尺寸需设置得很小（＜100nm），则会导致计算量太大，影响计算效果。为了减少自由度数，节约计算资源，对电极区使用等效密度法进行了处理。考虑到电极对系统的影响主要表现在降低了厚度剪切模态的基频，使系统呈现“能陷效应”［6］。因此，只要保证模型对基频的影响不变，就能正确地反应系统的“能陷效应”。假设电极随晶片表面作刚体运动，对于非电极区，其基频为

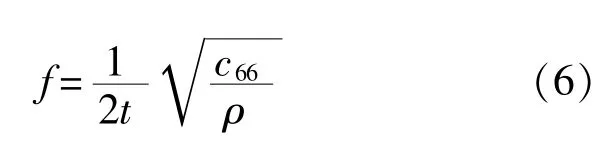
而电极区的基频为

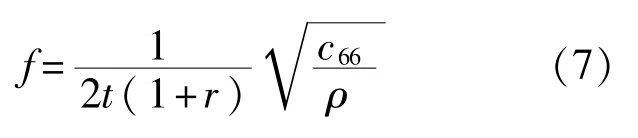
ρ——石英晶体密度；

t——晶片厚度。

将式（7）改写为

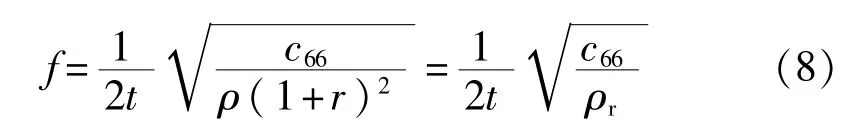
这里的ρr=ρ（1+r）2，称为“等效密度”。这样使得电极区与非电极区的差别仅在于密度不同，而厚度相同，从而便于单元划分。所建立的有限元模型如图1所示。

图1　有限元模型网格图

2.2边界条件及材料参数确定

晶体谐振片的夹具为橡胶密封圈，橡胶与石英晶片的固有频率相差105以上，而橡胶与晶片间的夹持力很小，因此，在有限元分析时将晶片的边界条件简化成自由边界。

AT切割石英晶体的力学和电学特性为各向异性，材料弹性系数矩阵为cij，压电系数矩阵为

表1　不同膜厚下谐振器频率的有限元分析结果

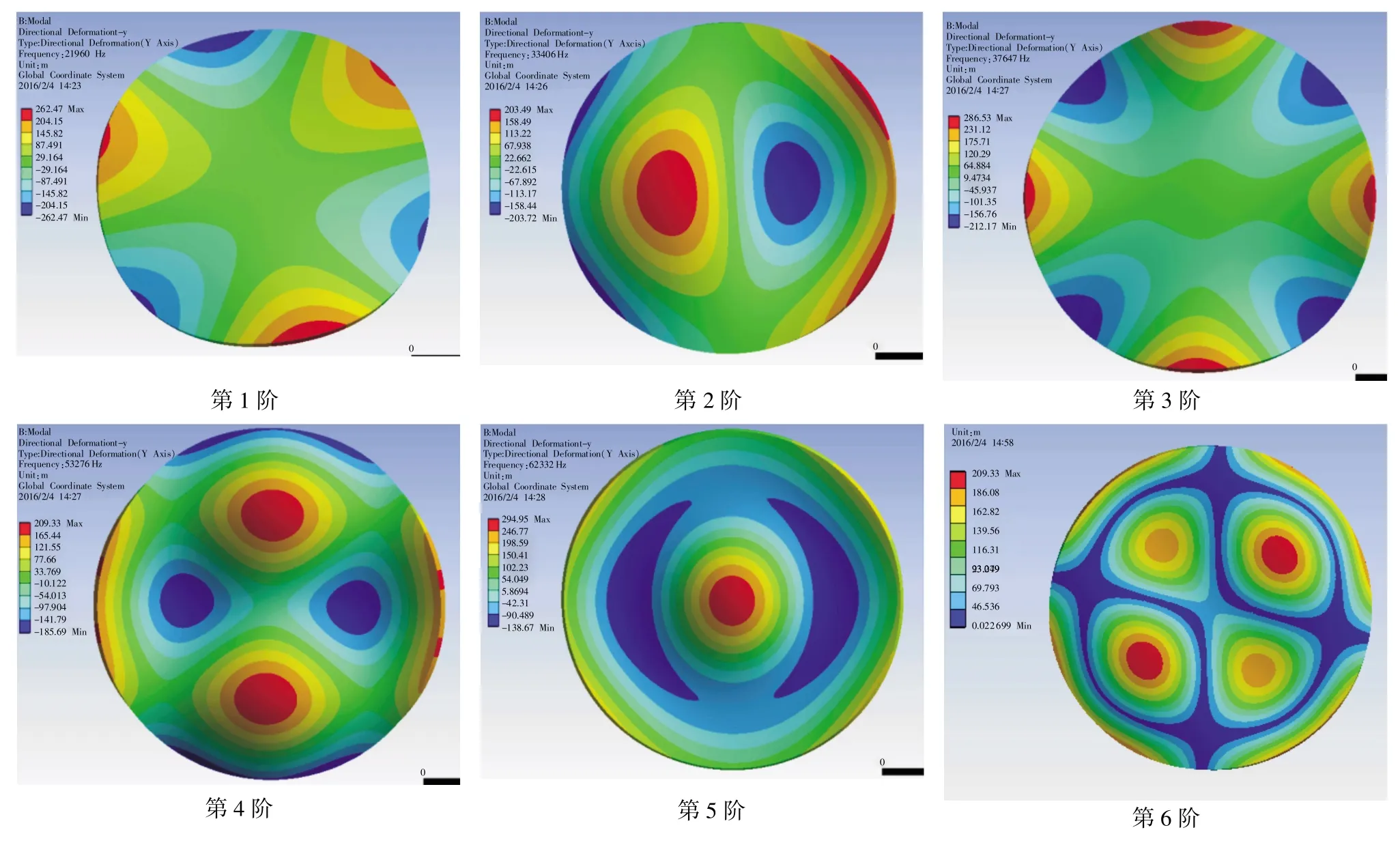
图2　谐振器低频振动时的前6阶模态图

介电常数矩阵为

2.3计算结果

利用上述有限元模型，计算了石英晶体谐振器在膜厚为0～50 μm情况下振动模态，图2为谐振器前6阶（低频时）模态的振型图。可以看出，该分析结果与文献［10］中通过实验方式采集到的振动模态基本一致，说明了该有限元模型和分析结果的有效性。

高频厚度剪切振动谐振频率的计算结果如表1所示。高阶厚度剪切振动的模态如图3所示。

图3　谐振器高频厚度剪切振动模态

3　实验及结果分析

为了验证理论和有限元的分析结果，使用石英晶体微天平系统进行厚度与频率之间关系的初步检测实验。实验时，首先将未镀膜的干净晶体谐振片接入测量电路，测量晶振片的谐振频率，然后断开电路，将晶振片连同夹具放置于喷枪下直接喷射包衣用的样品，待样品干燥后，接入检测电路测量并记录其谐振频率，最后取出晶振片，使用台阶仪测量其表面薄膜厚度。测量结果如表2所示。由于实验时采用直接喷射镀膜的方式，所以表中晶片上的膜厚具有一定随意性。

表2　不同膜厚下谐振器频率的实测结果

图4为晶体谐振器的谐振频率随包衣（附着物）厚度变化关系的理论计算、有限元分析和实验测试结果。理论计算、有限元分析和实验结果均具有较好的一致性，结果显示：包衣厚度每增加1μm，晶体谐振频率约降低12kHz。

由图4可以看出实测结果与理论分析结果有一定的误差，可能是因为包衣材料的密度与理论计算时所取密度值有较大差距的原因，但是基本反映了晶振片频率的变化趋势。图5给出了实测值的线性拟合结果，可以看出谐振片的检测灵敏度约为7.57kHz/μm。

图4　晶体谐振频率随膜厚的变化关系

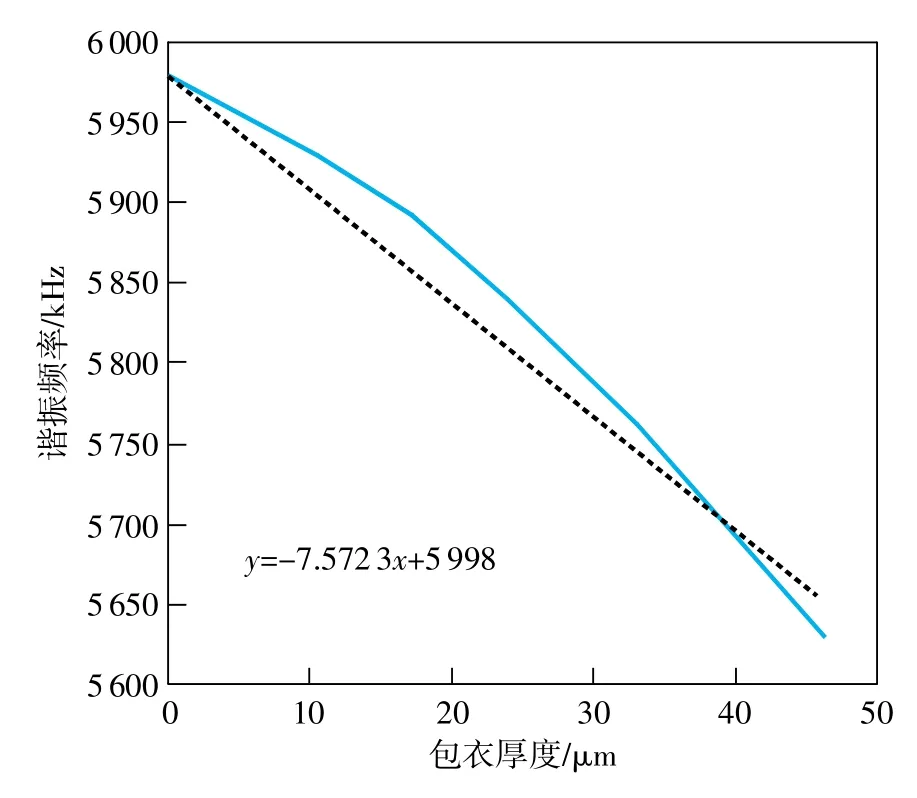
图5　实测数据拟合结果

4　结束语

目前对制药包衣厚度测量的方法研究较多，但均着眼于射线测量，为成品质量检测手段，不能做到包衣时的实时在线监测。基于石英晶体振荡技术的包衣厚度测量方法可以将膜厚测量和控制集中于一体，有效控制成膜质量。本文从理论上研究了石英晶体谐振片的谐振频率漂移量与包衣厚度之间的定量关系，理论计算结果显示，包衣厚度每增加1μm，晶体谐振器的谐振频率约降低12kHz。采用等效密度法建立的有限元法分析模型，可以有效地分析石英晶体谐振器的振动模态，数值分析的结果与理论值较为接近，实测实验也得到了相似的结果。

通过理论、有限元分析和实验方法验证了将石英晶体谐振原理用于制药包衣厚度测量的可行性，为进一步设计包衣厚度在线监控系统提供了理论依据和基础。

［1］BIKIARIS D，KOUTRI I，ALEXIADIS D，et al.Real timeandnon-destructiveanalysisoftabletcoating thickness using acoustic microscopy and infrared diffuse reflectance spectroscopy［J］.International Journal of Pharm aceutics，2012，438（1-2）：33-44.

［2］邱素君，何雁，张国松，等.近红外光谱快速测定柴胡总皂苷肠溶片包衣膜厚度研究［J］.中国药学杂志，2013，48（24）：2128-2133.

［3］赵亚佩，陈宁.拉曼光谱无损检测技术在医学上的应用［J］.数理医药学杂志，2011，24（5）：595-597.

［4］朱小平，杜华，王蔚晨.X荧光光谱分析法在镀层厚度测量中的应用［J］.计量学报，2008，29（4）：22-26.

［5］BROCK D，ZEITLER J A，FUNKE A，et al.Evaluation of critical process parameters for inter-tablet coating uniformity of active coated GITS using Terahertz Pulsed Imaging［J］.EuropeanJournalofPharmaceuticsand Biopharmaceutics，2014（7）：1-9.

［6］MINDLIN R D，SPENCER W J.Anharmonic，thicknesstwist overtones of thickness-shear and flexural vibrations of rectangular，AT-cut quartz plates［J］.J Acoust Soc Amer，1967（42）：1268-1277.

［7］王骥，史俊，杜建科.基于ANSYS的石英晶体谐振器厚度剪切振动的有限元分析 ［C］∥IEEE，Proceedings of the Symposium on Piezoelectricit，2010：527-531.

［8］YANG L，VITCHEV N，YU Z P.Modal analysis of practical quartz resonators using finite element method［J］. IEEETransactionsonUltrasonicsFerroelectricsand Frequency Control，2010，57（2）：292-298.

［9］李辉.石英晶体谐振器的振动模态分析及环境电磁场影响研究［D］.成都：西南交通大学，2013.

［10］HUANG C H，LIN Y C，MA C C.Theoretical analysis and experimental measurement for resonant vibration of piezoceramiccircularplates［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，2004，5l（1）：12-24.

（编辑：李刚）

Analysis and experimental study of quartz crystal oscillation frequency of drug coating thickness measuring system

HE Gaofa，ZHOU Chuande，REN Jianbing，MA Xia
（School of Mechanical and Power Engineering，Chongqing University of Science and Technology，Chongqing 401331，China）

Amethodtomeasurecoatingthicknessesbasedonthetheoryofquartzcrystal oscillation was put forward in order to improve the effect and quality of tablet coating and online monitoring.To be specific，the piezoelectric effect theory of quartz crystal was employed to analyze the functional relationship between the resonant frequency of quartz crystal resonator thickness shearing vibration and the coating thickness.Meanwhile，an equivalent density method was used to create a finite element model（FEM）to study the modality and resonant frequency of the resonator under different film thicknesses.The theoretical and FEM outcomes have revealed that the resonant frequency declines with the increase of the film thickness and presents an approximate linear relation，and the detection sensitivity is about 12 kHz/μm.The findings indicate that the proposed method can be applied to measure pharmaceutical coating thicknesses in real time.

quartz crystal oscillation；film thickness；coating；finite element method

A

1674-5124（2016）05-0028-05

10.11857/j.issn.1674-5124.2016.05.006

2016-01-07；

2016-02-20

重庆市基础与前沿研究计划项目（cstc2013jcyjA70005，cstc2015jcyjB0091）

何高法（1972-），男，安徽舒城县人，教授，博士，研究方向为微纳米精密测量、微机械传感器等。