回报和成本双重不确定下的信息化项目投资决策研究

陈丽娜 杨一平

摘要：探讨了回报和成本多重不确定下，企业信息化项目的投资决策问题。针对信息化项目风险高、耗时长、投资不可逆、项目回报非直接利润等特点，应用几何布朗运动和泊松过程表示项目回报和成本变量的多重不确定性，构造信息化项目投资决策模型。应用实物期权和动态规划理论对模型进行推导。结果表明，信息化项目回报和成本变量的不确定性，通常会对信息化项目投资的等待产生正向的激励；然而，成本和回报变量之间相关性的增加却会对等待产生负向的激励。

关键词：信息化投资，不确定投资，多重不确定性

DOI：10.13956/j.ss.1001-8409.2016.04.28

中图分类号：F062.4；F224文献标识码：A 文章编号：1001-8409（2016）04-0131-04

Abstract：This paper focus on the investment decision of informatization projects under multi uncertainties. An improved real option investment decision model is built based on the characteristics of informationization project： highrisk，timeconsuming， irreversible investment and no directly economic return. It uses Geometric Brownian motion and Possion process to describe the multi uncertainties of profits and costs， and then solve the model. The results show that the uncertainties of profits and costs would generate positive incentives on investment waiting， but the correlation between profits and costs would have negative incentive on investment waiting.

Key words：informatization investment； investment under uncertainty； multiply uncertainties

1引言

高投资回报是信息化建设者和管理者追求的目标，然而信息化建设的高失败率和信息化科学投资决策方法的相对缺失一直困扰着实业界。究其投资收益不甚理想的根源，信息化建设具有自身特有的复杂性，致使传统领域的投资理论和方法往往适用性不佳。如何在考虑信息化建設特有的复杂性前提下做出科学的投资决策则是这一难题需要解决的首要任务。而在信息化领域，现有研究成果大多沿袭“以评价带动管理、从管理中提升投资收益”的思路，由于评价理论自身的局限性，并不能妥善的解决项目投资时机问题。实物项目投资研究相对成熟，其所应用的理论和方法可以给信息化投资研究提供可靠的借鉴。

2文献研究综述

21信息化项目投资问题

国外学者对信息化项目投资问题的研究，主要应用数学和金融的方法。一些学者将学习曲线应用到软件和硬件的升级投资决策研究中。S.Dardan研究并介绍了Intel公司怎样把时间常数学习曲线用于操作系统和硬件系统的升级决策[1]。O.Ngwenyama采用S型学习曲线研究了软件的升级决策问题[2]。R.D.VanZee和S.Spinler研究了公共信息化创新项目中不确定因素对投资上限和下限的影响 [3]。

而国内研究，则主要以评价理论为基础。大量文献从信息化水平和绩效评价的角度对信息化投资进行探讨。设计一套科学合理的指标体系是信息化绩效评价的前提和关键。现有研究中常用的方法包括成熟度模型、平衡计分卡、基于资源基础论（RBV）的IT资源理论、数据包络分析（DEA），以及回归分析等方法[4～10]。

研究发现，信息化绩效评价成为企业信息化建设与管理的一种重要工具。然而由于评价理论自身的局限性，在项目投资时机选择问题上，仅依靠评价的理论和方法来解决投资时机选择这一关键难题还并不足够。

22不确定投资问题

上世纪80年代以来，不确定条件下的投资问题吸引了大批研究者。其中，颇具代表性的研究成果是Dixit和Pindyck关于不确定投资的论著，作者把项目投资中所面临的复杂环境中的不确定所导致的结果（项目的最终价值）定义为不确定的，该论著的理论成果成为后续许多研究的理论基础[11]。

如何根据项目自身的特点对项目价值的不确定性进行描述，进而将这些因素用科学的数理模型表示是研究者们主要关注的焦点。范颖和朱磊用几何布朗运动模拟油价、利率、投资环境的不确定，建立中国一个原油投资的模板[12]。Enrico Pennings和Luigi Sereno分别用泊松跳跃和几何布朗运动表述技术不确定和经济不确定环境，建立复合期权方法评价制药研发项目投资[13]。Young-ChanLee和Seung-SeokLee使用实物期权分析评价RFID技术采纳，并引入梯形模糊数表述收入和成本的不确定，得到期权方法中预期现金流以及预期成本是单个数值的情况[14]。杨安洋采纳奈特不确定来刻画风险，并在此基础上构建了模糊规避偏好和投资有成本可逆条件下企业投资决策模型[15]。尤代明和杨晓辉在传统的对称双寡头时间决策期权博弈模型上，引入泊松跳跃过程，描述技术换代对市场的影响，并建立技术换代的实物期权博弈模型[16]。

不确定投资理论已经广泛应用于包括信息技术在内的诸多实物项目的投资决策中。专家和学者们对不确定性的识别和数理描述研究已经有了一定的基础，可为本文的研究提供扎实的理论依据。

3模型建立

31模型建立与最佳投资时机

通过文献研究发现，在信息化领域内，应用实物期权方法进行项目投资的研究往往局限在项目价值的单一不确定性上。而在投资的实际过程中，项目价值是由项目未来回报和项目成本共同构成的。此外，由于信息化非直接经济效益的特点，在项目回报方面，存在多个回报变量。因此，单不确定性的投资模型在以解决信息化项目的投资决策问题上还存在一定的不足。

本文定义信息化项目价值的不确定性包括项目未来回报与成本的双重不确定性，其中回报和成本分别受到多个不确定变量的影响，研究假定项目回报V服从多因素的几何布朗运动和向下跳的泊松过程，项目成本I服从几何布朗运动。

dV=αVVdt+σzVdz+σwVdw-Vdq（1）

dI=αIVdt+σIVdκ（2）

其中，dz定义为维纳过程的增量，αV和αI分别为项目未来回报和项目成本的漂移参数；σi（i=w，z，I）为方差参数。λ为事件的平均发生率，在无穷小的时间区间dt上，事件发生的概率为λdt，而事件不发生的概率为1-λdt。假设新技术的一旦投入市场，项目回报V将以1的概率下降Ф个百分比。其中：

E（dz2）=dt， E（dω2）=dt， E（dκ2）=dt，

E（dzdω）=ρ1t， E（dzdκ）=ρ2t， E（dωdκ）=ρ3t

项目投资期权的价值取决于项目成本和项目未来回报。当V过低或者I过高的时候，期权将被持有，而当V大于I到达一定程度时，期权将被执行。

假设项目未来的利润流为P，

V（P）=PδP（3）

δP为P的便利收益。信息化项目的期权价值F（V（P），I），考慮1个单位期权，m个单位项目价值和n个单位项目成本所组成的投资组合：F-mP-nI。

通过伊藤引理展开d（F-mP-nI），由于期权价值函数包含跳跃过程，存在离散点，不能简单得用伊藤引理进行展开。因此，本研究首先对项目未来回报进行分析，然后选择价值函数的极端情况对项目期权进行研究。

32项目未来回报模型

dV=αVdt+σzVdz+σwVdw-Vdq（4）

项目未来回报V在一段是时间内将以几何布朗运动波动，而新技术投入市场后，将向下跳Ф个百分比，在事件发生后，继续以几何布朗运动波动。

这里需要泊松过程与几何布朗运动伊藤引理进行展开，则

E（dF）=αVF′（V）dt+12σzV2F″（V）dt+12σωV2F″（V）dt+ρ1σzσωF″（V）dt-λ{F（V）-F[（1-φ）V]}dt（5）

在投资机会价值F（V）的贝尔曼方程（投资机会的预期总回报等于其资本的预期增值率）为：

rFdt=E（dF）（6）

将式（5）带入（6） ，得：

rFdt=αVF′（V）dt+12σzV2F″（V）dt+12σωV2F″（V）dt+ρ1σzσωF″（V）dt-λ{F（V）-F[（1-φ）V]}dt（7）

项目的期权价值F满足价值匹配条件和两个平滑粘贴条件：

F（V*）=V*-I（8）

F′（V*）=1 （9）

F（0）=0 （10）

为满足上述条件，F（V）的解形式可表示为：

F（V）=AVβ（11）

β为上述转换后的非线性方程（12）的较大正根（用r-δ代替α）：

（r-δ）β+12（σ2z+σ2w+2ρ1σ1σw）*

β（β-1）-（λ+γ）+λ（1-）β=0（12）

此时，项目的最佳回报V*可表示为：

V*=ββ-1I （13）

当项目未来回报超过V*，应立即行使期权，进行投资。

33综合模型

令λ=0，对项目期权价值进行研究。

d（F-mP-nI）=（FP-m）dP+（FI-n）dI+12（σ2zP2FPP+12σ2ωP2FPP+ρ1σzσωFPP+12σ2κI2FII+ρ2σzσκFPI+ρ3σκσωFPI）（14）

选择FP=m，FI=n，则在（t，t+dt）在这段时间间隔内，投资的持有者有确定的资本收益：

（12σ2zP2FPP+12σ2ωP2FPP+ρ1σzσωP2FPP+12σ2κI2FII+ρ2σzσκPIFPI+ρ3σκσωPIFPI）（15）

为了得到期权不被执行的持有区域，上述确定收益与价值与成本的便利收益的支付（mδVP+nδII）dt的和，等于无风险的回报r（F-mP-nI）dt，整理后，

（12σ2zP2FPP+12σ2ωP2FPP+ρ1σzσωP2FPP+12σ2κI2FII+ρ2σzσκPIFPI+ρ3σκσωPIFPI）+（r-δV）PFP+（r-δI）IFI-rF=0（16）

在最优的立即执行区域，根据价值匹配条件和平滑粘贴条件：

F（P，I）=V′（P）-I=PδP-I（17）

FP（P，I）=V′（P）-I=1δP （18）

FI（P，I）=-1（19）

根据以上边界条件，可得到在等待区域F的解。

项目价值和项目成本的增加不能单纯的导致项目净值的增加，项目投资最优决策取决于p=PI，而期权价值在（P，I）内为一次齐次式，所以

F（P，I）=If（PI）=If（P）， f为某已知函数。则F的偏微分为：

FP（P，I）=f′（p）（20）

FI（P，I）=f（p）-pf′（p）（21）

FPP（P，I）=f″（p）I（22）

FPI（P，I）=-pf″（p）I （23）

FII（P，I）=p2f″（p）I（24）

将上述公式带入（15） ，得到：

（12σ2z+12σ2w+ρ1σzσw+12σ2κ

-ρ2σzσκ-ρ3σκσw）p2f″（p）

+（δI-δP）pf′（p）-δ1f（p）=0

（25）

价值匹配条件和平滑粘贴条件为：

f（p）=pδP-1（26）

f′（p）=1δP（27）

f（p）-pf′（p）=-1（28）

将上述公式带入（25），得到

（12σ2z+σ2w+2ρ1σzσw+σ2κ

-2ρ2σzσκ-2ρ3σκσw）β（β-1）

+（δI-δP）β-δ1=0（29）

令β1表示（25）的较大正根，则

P*I*=p*=β1β1-1δP（30）

此射线将等待区域与实行区域分开。

4数值分析

41项目未来回报模型数值分析

令Ф=1，r=δ=005，A=1，应用Matlab程序对式（11）、（12）和（13）进行求解，研究各要素对V*的依赖性。

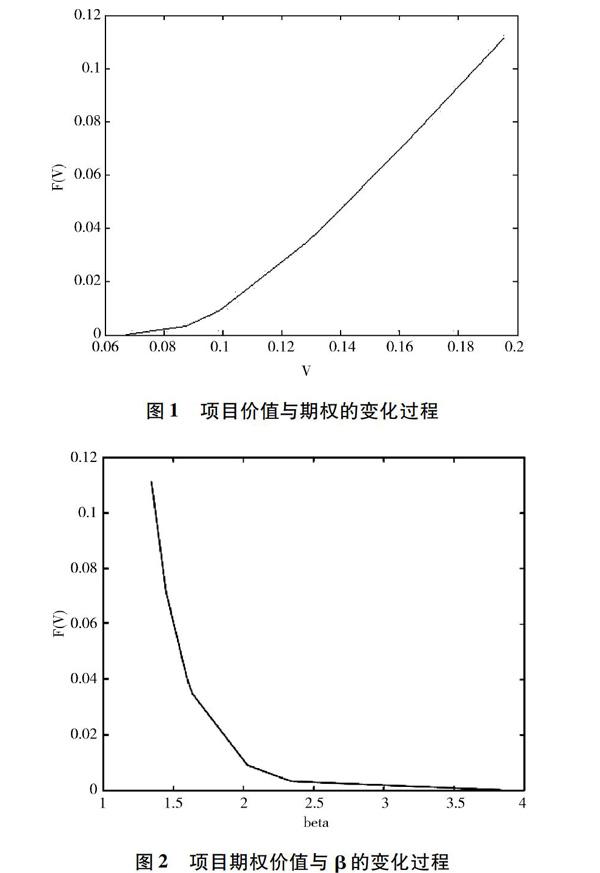
通过图1可以看出，项目的期权价值F（V）是V的凹函数，随着V*的增加而加速增加。F（V）随着β的增加而减小，说明较小的β使项目具有更高的期权行使价值。

通过表1可以看出，λ的存在降低了项目的未来回报，期权有更大的可能被执行，即在技术复杂多变的市场情形下，尽快采取行动可能是最佳的投资决策。而随着σz和σw以及这两者的相关系数ρ的增加，V*也随之升高。这说明不确定性的增加，使等待变得更有价值。

42综合模型数值分析

令δp=δI=005，对式（28）、（29）和（30）进行求解，研究各要素对p的依懒性。注意，为了使模型更加直观，本文在双随机不确定模型中，用未来利润流P代替V来表示项目投资后，为企业带来的价值。但是P不等于V，p*可以理解为期权的价值乘数。

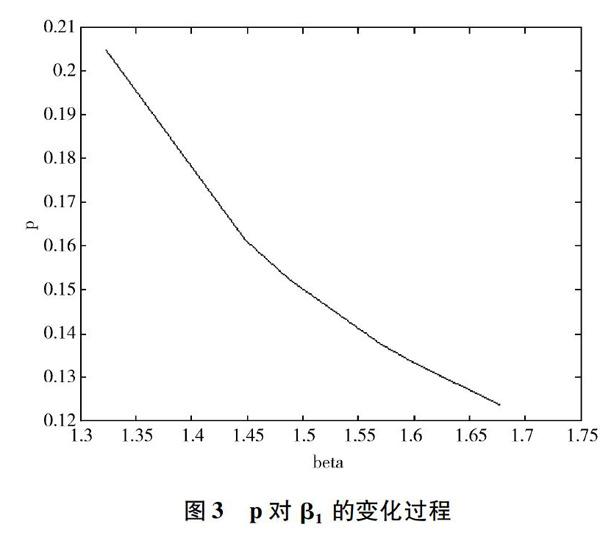
通过图3可以看出，p随着β的增加而减小，较小的β1可以获得更大的期权价格乘数，增加了期权被持有，项目等待的价值。而当p大于p*时，就是项目的最佳投资时机。

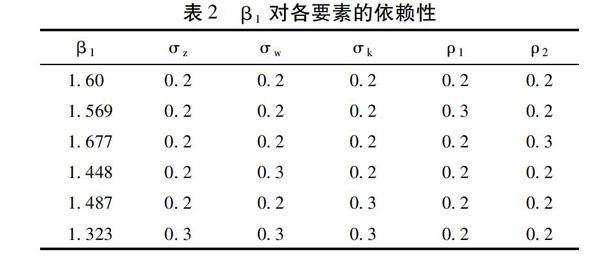
通过表2可知，随着项目未来利润和项目成本中不确定因性的增大，以及回报和成本变量间相关系数ρ的增大都会导致β1的减小，从而获得较大的期权价格乘数，使等待变得更有价值。然而，成本与回报变量间的相关系数ρ2的增加却导致β1的增加，导致较小的价值乘数。这使得项目等待的不再那么有利。

5结论

本文针对信息化项目的具体特点，建立了回报和成本双重不确定性的信息化项目投资模型。改进了不确定投资传统的项目价值不确定的单不确定模型，使得模型更贴近信息化投资的实际情况。并对模型进行推导和数值分析。其结果表明：信息化项目回报和成本的不确定性，通常对信息化项目投资时的等待有着正向的激励作用；成本和回报变量间的相关性却会对等待产生负向的激励。组间的相关性提升了项目等待的价值，使得信息化投资行为被延后，而组外的相关性的增加却促使投资行为被执行。

信息化项目投资是一个复杂的过程，在模型建设时，还应针对信息化项目本身的固有特点进行更为细化的分类研究。这也是本文需要进一步深入的方向。

参考文献：

[1]DARDAN S， BUSCH D， SWARD D. An Application of the Learning Curve and the Nonconstant- growth Dividend Model： IT Investment Valuations at Intel Corporation[J]. Decision Support Systems， 2006， 41（4）： 688-697.

[2]NGWENYAMA O， GUERGACHI A， MCLAREN T. Using the Learning Curve to Maximize IT Productivity： A Decision Analysis Model for Timing Software Upgrades[J]. International Journal of Production Economics， 2007， 105（2）： 524-535.

[3]Roger D. Van Zee， Stefan Spinler. Real Option Valuation of Public Sector R&D Investments with A Down-and-out Barrier Option[J]. Technovation， 2014， 34（8）： 477-484.

[4]左美云， 陳蔚珠， 胡锐先. 信息化成熟度模型的分析与比较[J]. 管理学报， 2005， 2（3）： 341-346.

[5]马慧， 杨一平. 企业信息化能力成熟度关键模型研究[J]. 经济与管理研究， 2010（1）： 73-78.

[6]Milis， K.， Mercken， R. The Use of the Balanced Scorecard for the Evaluation of Information and Communication Technology Projects [J].International Journal of Project Management， 2004， 22（2）： 87- 97.

[7]王铁男， 李一军， 刘娇. 基于BSC的企业信息化绩效评价应用研究[J]. 中国软科学， 2006（4）： 136-147.

[8]张嵩， 吴绪永. 基于RBV的企业信息化绩效评估层次模型[J]. 科学学与科学技术管理， 2007（6）： 129-133.

[9]杨一平， 马慧， 张婀莉， 戴利. 企业信息化投入产出定量分析模型研究[J]， 信息资源管理学报， 2014（2）： 67-71.

[10]陈海声， 卢丹. 研发投入与企业价值的相关性研究[J]. 软科学，2011年 2月，第 25卷（2）：20-23.

[11]Dixit A K， R S. Pindyck. Investment under Uncertainty[M]. Princeton University Press， 1994.

[12]Ying Fan， Lei Zhu. A Real Options Based Model and Its Application to Chinaese Overseas Oil Investment Decisions[J]. Energy Economics， 2009， 32（3）： 627-637.

[13]Enrico Pennings， Luigi Sereno. Evaluating Pharmaceutical R&D under Technical and Economic Uncertainty[J]. European Journal of Operational Research， 2011， 212（2）： 374-385.

[14]Young-Chan Lee， Seung-Seok Lee. The Valuation of RFID Investment Using Fuzzy Real Option[J]. Expert Systems with Applications， 2011， 38（10）： 12195-12201.

[15]杨安洋， 杨正勇. 奈特不确定条件下企业有成本可逆投资策略研究[J]. 数学的实践与认识， 44（13）： 125-136.

[16]You Daming， Yang Xiaohui. Option Game with Poisson Jump Process in Company Radical Technological Innovation[J]. Technological Forecasting & Social Change， 2014， 81： 341-350.

（責任编辑：石琳娜）