磁各向异性电各向同性介质中电磁场矢势达朗贝尔方程的具体坐标形式
李文略
(湛江师范学院 基础教育学院,广东 湛江 524037)
磁各向异性电各向同性介质中电磁场矢势达朗贝尔方程的具体坐标形式
李文略
(湛江师范学院 基础教育学院,广东 湛江524037)
磁各向异性电各向同性介质中电磁场矢势达朗贝尔方程是张量方程。由张量方程的协变性,应用张量分析的矩阵方法推导出电磁场矢势达朗贝尔方程在球坐标系和柱坐标下的具体形式。
磁各向异性;电各向同性介质;电磁场矢势;达朗贝尔方程;张量分析;矩阵
陈燊年、洪清泉等[1]推导得到了磁各向异性(文中的磁各向异性是指有且仅有3个正交主轴方向)电各向同性介质中电磁场矢势达朗贝尔方程(简称介质异性达朗贝尔方程),并推导出了该方程在主轴坐标系下的具体形式,但没有推导出其在常用曲线坐标系下的具体形式。达朗贝尔方程是研究磁各向异性电各向同性介质中电磁场的重要方程[1-3],采用何种坐标系表述达朗贝尔方程视求解相关的电磁场问题的方便而定,因此有必要对其在常用曲线坐标系下的具体形式进行研究。李洲圣,唐长红[4]系统的定义了张量分析的矩阵方法,文[5-6]应用该方法研究了介质为各向异性的电磁场。本文将从达朗贝尔方程出发,应用张量分析的矩阵方法推导出达朗贝尔方程在球坐标系和柱坐标系下的具体形式。
1 介质异性达朗贝尔方程及在直角坐标系的表达式
陈燊年[1]等应用麦克斯韦方程组、电和磁各向异性介质的电磁性质方程和电荷守恒律,并在满足洛伦兹条件的情况下,推导得到了磁各向异性电各向同性介质中电磁场矢势达朗贝尔方程为
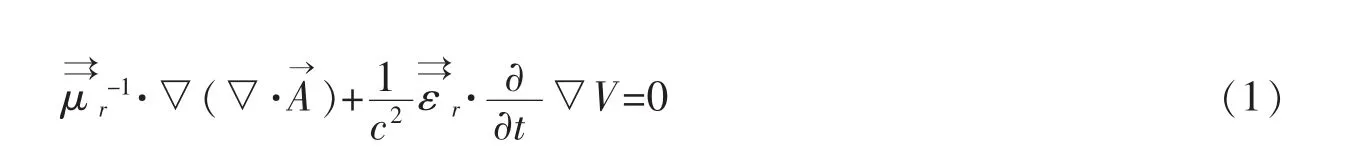

并由式(2)推导出了该方程在笛卡尔直角坐标系下的具体表达式为[1]

2 介质异性达朗贝尔方程在球坐标系的表达式
以磁各向异性的3个正交主轴为坐标轴建立笛卡尔坐标系O-xyz,记为χ→(i→1,i→2,i→3),χ→T为χ→的转置形态。建立球坐标系,坐标参量为r(球半径),θ(极角),φ(方位角);协变球坐标系记为ψ→(e→r,e→θ,e→φ),e→r、e→θ、e→φ为协变坐标基矢量,ψ→T为ψ→的转置形态;逆变球坐标系记为Ψ→=(h→r,h→θ,h→φ),h→r、h→θ、h→φ为逆变坐标基矢量,Ψ→T为Ψ→的转置形态。设电磁场矢势A→在协变球坐标系下逆变物理分量分别为Ar、Aθ、Aφ。
现计算式(2)中等号左边第一项
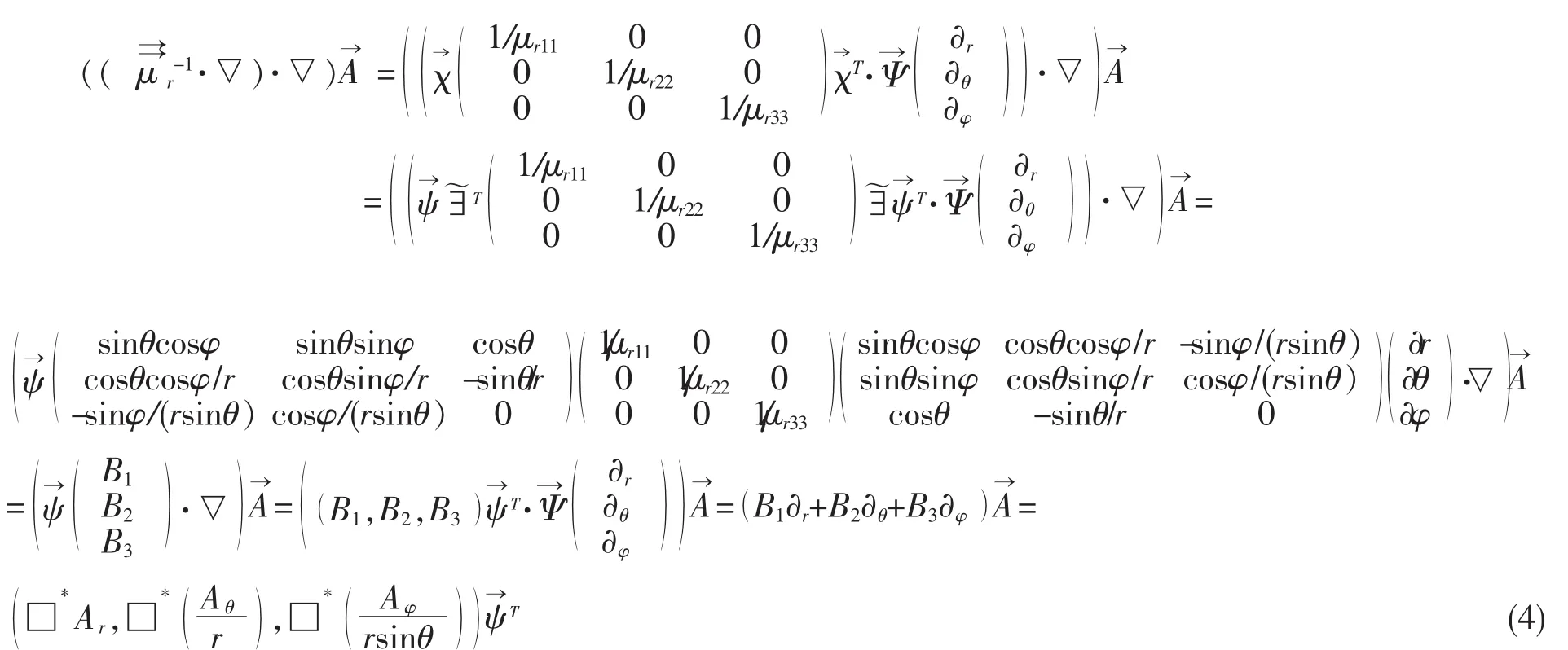

计算式(2)等号左边第二项和右边的项

式(6)中,jr、jθ、jφ分别为→在协变球坐标系下的逆变物理分量。
由式(4)(5)(6)可得电磁场矢势的达朗贝尔方程在球坐标系下的具体形式

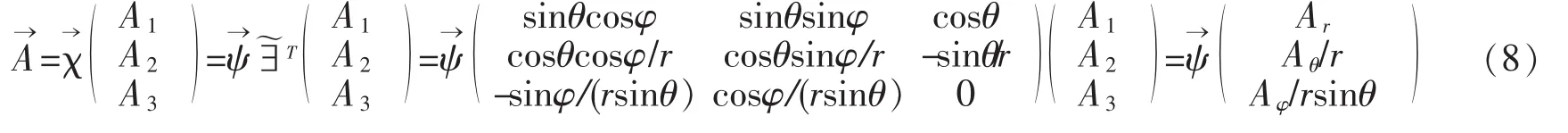
由式(8)可得A→的变换关系同理可得的变换关系:
3 介质异性达朗贝尔方程在柱坐标系的表达式
以磁各向异性介质的3个正交主轴为坐标轴建立笛卡尔坐标系O-xyz,记为建立柱坐标系,坐标参量为r,φ,z;协变柱坐标系记为为协变坐标基矢量;逆变球坐标系记为为逆变坐标基矢量。设电磁场矢势在协变柱坐标系下的逆变物理分量为Aρ、Aφ、Az。
现计算式(2)中等号左边第一项

计算式(2)等号左边第二项和右边的项

式(11)中,jρ、jφ、jz分别为j→在协变柱坐标系下的逆变物理分量。
由式(9)(10)(11)可得电磁场矢势的达朗贝尔方程在柱坐标系下的具体形式

若令μr11=μr22=μr33=μr,则可得电和磁各向同性电介质中的电磁场矢势的达朗贝尔方程在柱坐标系下的具体形式与式(12)形式一致,其电磁算符□'的具体形式为
与前文式(8)推导的过程一样,可得A→和j→在笛卡尔坐标系和柱坐标系下具体形式的变换关系为
4 结语
研究电和磁各向异性介质的电磁场,张量分析的矩阵方法不失为一种有益的数学方法,应用它可方便的推导出磁各向异性电各向同性介质中电磁场矢势达朗贝尔方程在球坐标系和柱坐标系下的具体形式。另外,本文能成功推导出该结果的关键是,式(2)表示的达朗贝尔方程是张量方程,其具有协变性,这一点有助于加深对磁各向异性电各向同性介质电磁属性的理解。由式(7)(12)可知达朗贝尔方程在球、柱坐标系下的具体形式是很复杂的,在μr11=μr22=μr33=μr的假设下,可过渡到电和磁各向同性介质的达朗贝尔方程在球、柱坐标系下的具体形式。
[1]陈燊年,洪清泉,王建成.介质为各向异性的电磁场[M].北京:科学出版社,2012:257-263.
[2]陈燊年,王建成.各向异性磁矢势A的微分方程及其解[J].华侨大学学报(自然科学版),1996,17(1):90-97.
[3]魏腾雄,苏武浔.各向异性介质中的波动方程[J].江西科学,2005,23(5):597-599.
[4]李洲圣,唐长红.三维空间张量分析的矩阵方法[M].北京:航空工业出版社,2010:10-25、154.
[5]李文略.电各向异性介质中泊松方程的具体形式[J].泉州师范学院学报,2015,33(2):93-96.
[6]李文略.各向异性磁介质中空间与空间的变换关系及应用[J].广西物理,2015,36(2):20-23.
(责任编辑:朱联九)
The Specific Coordinate Forms of d'Alembert Equation of Vector Potential in Magnetic Anisotropic and Electric Isotropic Medium
LI Wen-lue
(College of Basic Education,Institute of Zhanjiang Normal University,Zhangjiang 524037,China)
d'Alembert equation of vector potential in magnetic anisotropic and electric isotropic medium is a tensor equation.Because the covariance of tensor equations,the specific expressions of d'Alembert equation are deduced in the spherical coordinate system and in the cylindrical coordinate system with matrix method of tensor analysis.
magnetic anisotropic;electric isotropic medium;vector potential;d'Alembert equation;tensor analysis;matrix
O441.4
A
1673-4343(2016)02-0006-04
10.14098/j.cn35-1288/z.2016.02.002
2015-10-19
李文略,男,广东茂名人,讲师。主要研究方向:张量分析和电磁场理论。

