干气密封的实际气体焦耳-汤姆逊效应分析

邓成香，宋鹏云，马爱琳



干气密封的实际气体焦耳-汤姆逊效应分析

邓成香，宋鹏云，马爱琳

（昆明理工大学化学工程学院，云南 昆明 650500）

干气密封系统中气体通过过滤器、阀门、孔板和密封端面等组件时会发生焦耳-汤姆逊（JT）效应，可能导致密封气温度降低，甚至出现液相凝析。焦耳-汤姆逊效应一般通过焦耳-汤姆逊系数来反映。针对干气密封常面临的氢气、氮气、空气和二氧化碳，利用VDW方程、RK方程、SRK方程和PR方程4个经典状态方程（EOS）分别计算了相应的焦耳-汤姆逊（JT）系数，并与文献实验数据进行了比较，选择最佳状态方程作出各气体的JT系数曲线和焦耳-汤姆逊反转曲线（JTIC），并利用编程计算出空气和氮气通过干气密封端面时，由于JT效应引起的气体温降。结果表明：实际气体的焦耳-汤姆逊效应，对干气密封的节流环节会产生重要影响。常温条件下，氢气发生致热效应，而氮气、空气和二氧化碳气体发生致冷效应。采用4种状态方程计算焦耳-汤姆逊系数时，RK方程的平均相对误差和最大相对误差最低且分别小于4%和10%。干气密封气体的实际气体焦耳-汤姆逊效应能引起较大的温度变化，其中气体介质压力比介质温度对温差的影响更大。压力较小时JT效应引起的温降可以忽略。

干气密封；实际气体；状态方程；焦耳-汤姆逊系数；反转曲线

引 言

实际气体流动过程，由于节流效应，气体发生绝热不可逆膨胀导致温度变化的现象称为焦耳-汤姆逊效应。气体在膨胀后温度降低，称为冷效应；温度保持不变时称为零效应；温度升高时称为热效应。密封气通过干气密封系统中过滤器、阀门、孔板和密封端面等组件时一般会发生焦耳-汤姆逊冷效应，导致密封气温度降低，并可能出现凝析现 象[1]。如果析出液体进入干气密封端面，就会改变干气密封的工况条件，导致气膜状态和作用力发生改变，从而影响干气密封的使用效果及使用寿命[2]，甚至导致密封失效等重大安全问题。许静等[3-4]利用求解雷诺方程和数值分析的方法对螺旋槽干气密封进行了研究，得出气体热黏效应对干气密封性能的影响。针对干气密封的研究一般把气体处理为理想气体，但是随着干气密封性能研究的不断深入，其应用范围从低速、常压扩大到高速、高压，且在高压工况下，气体的行为与理想气体有较大差异[5-6]。通过分析、评价密封气的焦耳-汤姆逊效应可以预先评估干气密封系统的安全可靠性能，并可采取有效措施克服由于焦耳-汤姆逊效应带来的不利影响。但是，到目前为止，尚未发现对干气密封封气介质的实际气体焦耳-汤姆逊效应的研究。

本文针对干气密封常面临的氢气、氮气、空气和二氧化碳，分析不同气体状态方程用于求解焦耳-汤姆逊系数的准确性，利用最佳状态方程作出JT系数曲线和JT反转曲线，并计算出干气密封中JT效应引起的空气在不同介质温度和不同外部压力时的温差。

1 焦耳-汤姆逊（JT）系数

实际气体在等焓节流过程中温度随压力的变化速率，即温熵图（-）中的等焓线上任一点的斜率称为焦耳-汤姆逊（JT）系数[7]。JT系数的准确计算对评价实际气体的焦耳-汤姆逊效应至关重要。焦耳-汤姆逊系数表达式[8]为

其中

式中，JT为JT系数，K·MPa-1；为温度，K；为压力，MPa；为摩尔体积，m3·mol-1；为压缩因子；为气体常数，8.314 J·mol-1·K-1；,real为实际气体的摩尔比定压热容，J·mol-1·K-1。

1.1 立方型状态方程

气体状态方程可化为的三次展开式，也可以根据化为的三次展开式，称为立方型状态方程，其形式简单，方程中一般只有两个常数，且常数可以通过纯物质临界性质和偏心因子计算。各气体的临界参数和偏心因子如表1所示。

表1 临界参数和偏心因子[10]

4种经典立方型状态方程式如下[11]。

VDW:

(3)

RK:

(4)

SRK:

(5)

PR:

(6)

以上4种立方型方程式（3）～式（6）中的参数，如表2所示。

表2 4种立方型状态方程的压缩因子展开式的参数[11]

对空气可视为由摩尔分数分别为0.7812和0.2188的氮和氧组成的二元混合气体。立方型状态方程中的参数和采用混合规则计算[12-14]

其中交叉项可按式（9）计算

式中，为氮气的摩尔分数；为氧气的摩尔分数；为氮气与氧气的二元交互作用参数。

1.2 压缩因子

虽然对压缩因子的研究比较丰富，有大量的实验数据和经验公式，但通过理论方法计算压缩因子的研究较少。本文用代入式（3）～式（6）得到状态方程的压缩因子三次展开式如式（10）所示，其中参数如表2所示。

利用卡尔丹公式[15]可解得符合条件的压缩因子值。

其中

得到符合条件的压缩因子值

1.3 实际气体摩尔比定压热容

实际气体的比定压热容,real既是温度的函数，又是压力的函数，它由理想气体的比热容（,ideal）和剩余比热容（∆c）两部分组成[16]。本文采用VDW方程、RK方程、SRK方程和PR方程的剩余焓（R）推导出剩余比热容（∆）的计算公式。

联立式（3）～式（6）和式（14）～式（16），即可得分别按照VDW方程、RK方程、SRK方程和PR方程推导出的剩余比热容（）的计算公式分别如下所示。

VDW：

RK：

SRK：

PR：

计算理想气体比定压热容公式[8]如式（21）所示，其中的参数见表3。

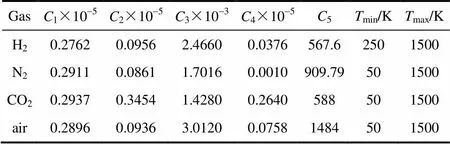
表3 理想气体比定压热容的参数[10]

联合式（2）、式（12）和式（13），可分别求得氮气、空气和二氧化碳在不同温度和不同压力下的JT系数，按照VDW方程、RK方程、SRK方程和PR方程计算的JT系数，与文献[10]的实验数据进行比较，部分结果如表4～表6所示。实际计算了压力分别等于0.1、1、2、6、10 MPa的数据，表4～表6示出了压力等于0.1 MPa和压力等于10 MPa的结果。各种压力下JT系数计算结果与文献实验结果的相对误差如表7所示。由于目前为止，尚未发现有关氢气的JT系数的实验数据，通过计算氮气、空气和二氧化碳的JT系数选择最佳状态方程，并认为该状态方程同样适用于计算氢气的JT系数。表中EXP表示来自文献[10]的实验数据，VDW、RK、SRK和PR分别表示利用相应方程求得的JT系数，RE表示相对误差，AVE表示平均相对误差，Min表示最小相对误差，Max表示最大相对误差。其中。

表4 不同温度和不同压力下氮气的JT系数计算结果比较

Note: Results are (JT/K·MPa-1)/(RE/%).

表5 不同温度和不同压力下空气的JT系数计算结果比较

Note: Results are (JT/K·MPa-1)/(RE/%).

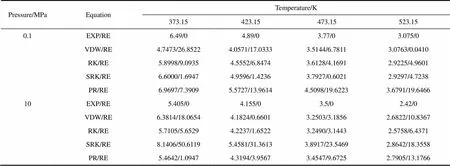
表6 不同温度和不同压力下二氧化碳的JT系数计算结果比较

Note: Results are (JT/K·MPa-1)/(RE/%).

通过利用VDW方程 、RK方程、SRK方程和PR方程分别计算氮气、空气和二氧化碳的JT系数与文献[10]实验数据比较，其计算的平均相对误差、最小相对误差和最大相对误差如表7所示。

表7 各种算法的相对误差对比

从表7可以看出：通过4种状态方程计算JT系数的误差分析，RK方程平均相对误差和最大相对误差最低且分别小于4%和10%。4种状态方程中，RK方程用于计算干气密封气的JT系数时，精度较高。

1.4 焦耳-汤姆逊（JT）系数曲线

通过对各种气体利用不同算法得到的JT系数与文献[10]的实验数据比较的平均相对误差可以看出：各种气体采用RK方程计算JT系数均能获得较高的精度。分别通过编程利用RK方程作出干气密封常用工业气体氢气、氮气、空气和二氧化碳对应的焦耳-汤姆逊系数曲线，如图1所示。

图1 4种气体的JT系数曲线

由图1可以看出：4种气体的JT系数均随温度和压力的升高而降低，且变化幅度逐渐减小。根据相同温度和压力下不同气体的JT系数比较，可判断4种气体的JT效应的冷效果由强到弱依次为二氧化碳、空气、氮气和氢气。

2 焦耳-汤姆逊反转曲线（JTIC）

对于实际气体，随着气体压力的升高，JT系数由大变小，甚至出现负值。JT系数从正值变到负值，必经过JT系数等于零的点。当JT系数为正值，即，发生致冷效应；当JT系数为负值，即，发生致热效应；当JT系数为零，即，为理想气体，既不致冷，也不致热。可通过的点来判断的正负，将一系列的点连接起来就形成一条曲线，称为焦耳-汤姆逊反转曲线（JTIC），即通过此曲线时，焦耳-汤姆逊效应反 转[17-20]。通过JTIC很容易判断出实际气体的致冷区域和致热区域。在低压侧，即在JTIC内侧是致冷区域；在高压侧，即JTIC外侧是致热区域。令，由式（2）可以得到JTIC方程表达式。

联合式（4）和式（22）化解得的方程为

按照式（10）～式（12）求压缩因子的方法将式（23）转化为卡尔丹公式形式，并解出用表示气体值的表达式为

其中

将式（24）代入式（4）得到温度与压力关系的JTIC方程表达式为

令(,)0，通过编程利用RK方程作出氢气、氮气、空气和二氧化碳对应的JTIC，如图2所示。

图2 4种气体的JT反转曲线

由图2可以清晰地看出：利用RK方程作出的4种气体JT反转曲线中，氢气和二氧化碳的JT反转曲线相差较大。二氧化碳反转曲线的温度范围为200～1600 K，最高转化压力超过80 MPa，二氧化碳极易发生致冷效应。而氢气的最高转化温度低于200 K，氢气只有在预冷到很低的温度时，节流后才会发生致冷效应。在常温情况下，氢气均发生致热效应。这在氢气的常温充装过程中，会发生温度升高现象，这正是氢气焦耳-汤姆逊致热效应的表现[21]。各种气体在反转曲线上对应的温度和压力工况，可视为理想气体，不发生焦耳-汤姆逊效应，或称为焦耳-汤姆逊零效应。但在干气密封的实际运行过程中，很难保证密封气的温度和压力能稳定在反转曲线上，所以干气密封很容易发生焦耳-汤姆逊致冷效应或致热效应。一般压力范围内的干气密封，氢气容易发生致热效应，而氮气、空气和二氧化碳气体容易发生致冷效应。

3 计算实例

3.1 JT效应引起的温差计算

考虑气体通过干气密封端面的焦耳-汤姆逊效应时，将气体通过干气密封端面的过程视为等焓节流膨胀过程，仅考虑JT效应引起的温度变化，即温差。其温差ΔH的定义式如下[22]

联合式（1）、式（4）、式（13）、式（18）和式（21）求得利用RK方程表示的JT系数

由于JT系数与压力可近似为直线关系[23]，为了提高ΔH的计算精度，采用辛普森数值积分法可将式（26）的温差ΔH的表达式转化为

用高级程序语言编程计算在不同介质温度o和不同外部压力o时温差ΔH的变化情况。不考虑密封端面的具体结构尺寸，仅考虑压差的变化。选择空气作为密封介质，环境压力为i0.1013 MPa，外部压力o为0.3～20 MPa，介质温度o为278～333 K。联合式（28）和式（29）计算所得的密封端面内外径的温差ΔH如表8所示。

表8 不同温度和压力下空气的温差变化

表8计算结果的合理性，可由文献[24]提供的案例得到支持。文献[24]提供的案例为：空气在293 K时，从1.013 MPa节流到0.1013 MPa，温度可降低到290.7 K，即下降2.3 K。在相同情况下由式（22）编制程序计算的温度下降2.22 K。两者吻合。利用高级程序语言编制的程序，将表8中的密封介质换成氮气，其他参数不变，计算密封端面内外径的温差ΔH如表9所示。

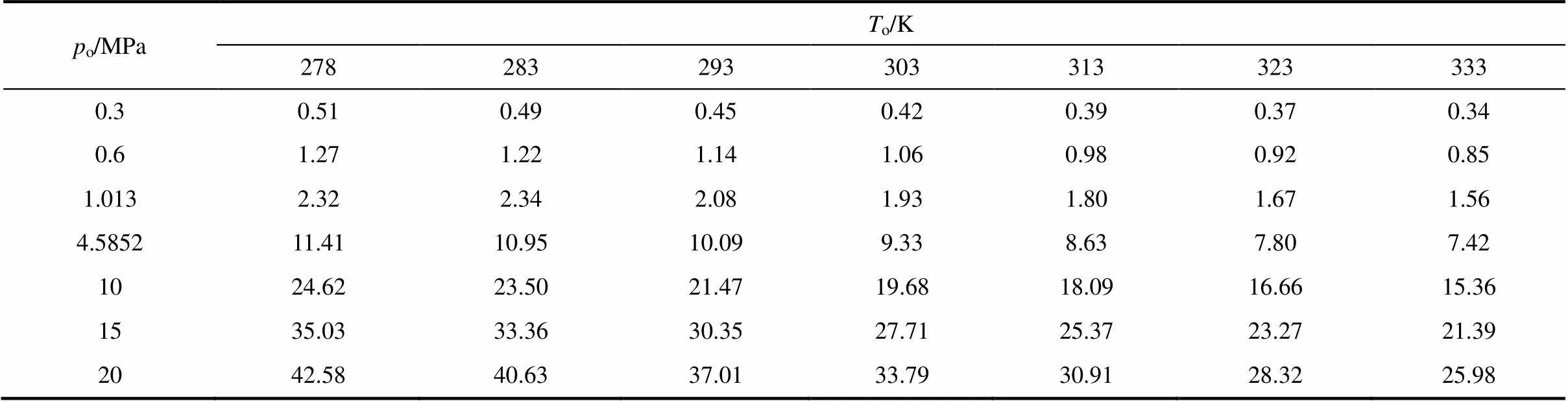
表9 不同温度和压力下氮气的温差变化

由表8和表9的数据可以看出，由于图2中空气和氮气的焦耳-汤姆逊系数曲线类似，且空气的JT系数略高于氮气，在相同工况下空气的温差均略大于氮气。两者的温差变化具有相同的规律，当介质温度一定时，温差随外部压力增大而增大。尽管JT系数随压力的增加而降低，但总的温差仍随压力的增加而增加。只不过低压区由于JT系数大对总体温差的贡献较大，而高压区由于JT系数小，对总体温差的贡献较小。当外部压力一定时，温差随密封介质温度增大而减小，这是因为JT系数随温度的增加而降低。外部压力比介质温度对温差的影响更大。干气密封封气介质的实际气体焦耳-汤姆逊效应能引起较大的温度变化，只有在压力较小时方可不用考虑。

3.2 空气含水的温差计算

考虑到空气含有水蒸气的情况，作出不同湿度下的空气对应的露点曲线，同时作出某一温度和压力下的膨胀线和JT效应引起的温降曲线。

将湿空气看为水和干空气的混合物，其安托因参数见表10[25]。利用安托因方程式（30）便可以计算出水的饱和蒸气压[26]。

表10 安托因参数[25]

对于湿空气来说，其相对湿度和湿度的表达式分别为

密封气流过密封端面、孔板等组件时，假设发生不可逆膨胀过程，其压力温度关系符合过程方程[27]

式中，1、1为膨胀初始压力和初始温度，2、2为膨胀后的压力和温度。为过程指数，绝热膨胀时，过程指数等于绝热指数，则。

利用高级程序语言编制程序，作出不同湿度空气的露点曲线，并在同一个图中作出初始温度和压力为373.15 K和10 MPa的膨胀线以及JT效应引起的温降线，同时将绝热膨胀和JT效应组合，作出两者共同作用引起的温降曲线如图3所示。

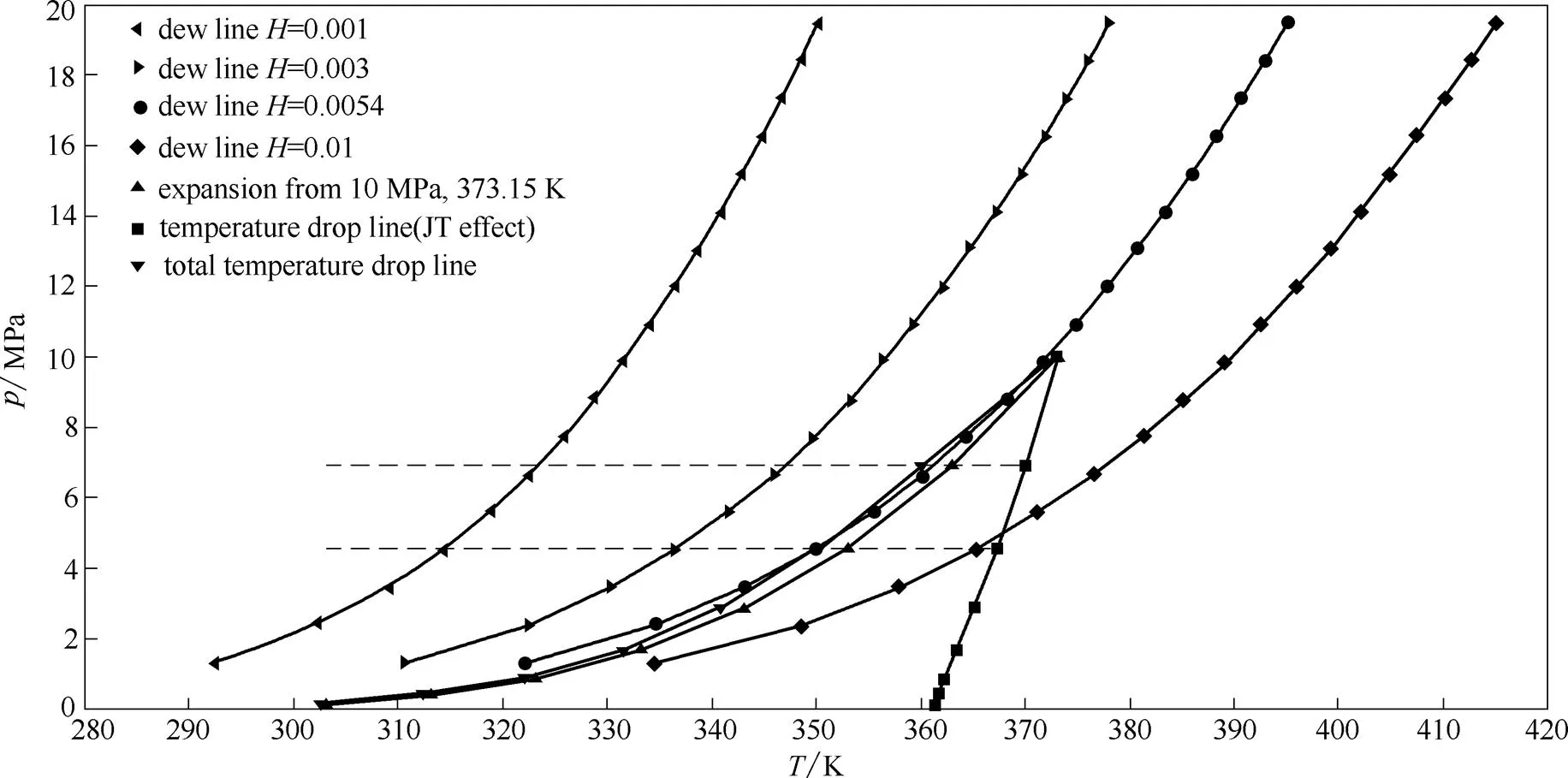
图3 露点线、膨胀线和JT效应引起的温降线

4 结 论

（1）实际气体的焦耳-汤姆逊效应，对干气密封的节流环节会产生重要影响。常温条件下，氢气发生致热效应，而氮气、空气、二氧化碳气体发生致冷效应。

（2）分析干气密封的焦耳-汤姆逊效应时，采用RK状态方程计算压缩因子和比定压热容,real较为合理。

（3）获得了一种计算焦耳-汤姆逊效应反转曲线的方法和程序。

（4）获得了一种考虑焦耳-汤姆逊效应确定节流温差的计算方法和程序。

References

[1] 钟桂香, 罗潇, 郗祥远. 干气密封失效原因分析与有效性措施 [J]. 油气储运, 2014, 33 (3): 335-339. DOI: 10. 6047/j.issn.1000- 8241.2014.03.026.
ZHONG G X, LU X, XI X Y. Failure analysis and effective measures in the dry gas seal [J]. Oil & Gas Storage and Transportation, 2014, 33 (3): 335-339. DOI: 10.6047/j.issn.1000-8241.2014.03.026.

[2] 马丽芳. 干气密封气析出液处理 [J]. 兰州石化职业技术学院学报, 2010, 10 (4): 7-9.
MA L F. Processing for separation fluid of dry gas seal gas [J]. Journal of Lanzhou Petrochemical College of Technology, 2010, 10 (4): 7-9.

[3] 许静, 彭旭东, 白少先, 等. 气体热黏效应对干气密封性能影响的数值分析 [J]. 上海交通大学学报, 2012, 46 (5): 722-728.
XU J, PENG X D, BAI S X,. Numerical analysis of gas thermal viscosity effect on performance of a spiral-groove gas face seal [J]. Journal of Shanghai Jiaotong University, 2012, 46 (5): 722-728.

[4] 许静, 彭旭东, 白少先, 等. 端面微尺度效应和热黏效应对干气密封性能的影响 [J]. 化工学报, 2013, 64 (9): 3291-3330. DOI: 10.3969/j.issn.0438-1157.2013.09.030.
XU J, PENG X D, BAI S X,. Effect of surface micro-scale and thermal viscosity on sealing performance of spiral-groove dry gas seal [J]. CIESC Journal, 2013, 64 (9): 3291-3330. DOI: 10.3969/j.issn.0438- 1157.2013.09.030.

[5] 丁雪兴, 刘勇, 张伟政, 等. 螺旋槽干气密封微尺度气膜的温度场计算 [J]. 化工学报, 2014, 65 (4): 1353-1358. DOI: 10.3969/j.issn.0438- 1157.2014.04.027.
DING X X, LIU Y, ZHANG W Z,. Calculation of temperature filed of micro-scale gas film in spiral groove dry gas seal [J]. CIESC Journal, 2014, 65 (4): 1353-1352. DOI: 10.3969/j.issn.0438- 1157.2014.04.027.

[6] 宋鹏云, 胡晓鹏, 许恒杰, 等. 实际气体对T槽干气密封动态特性的影响 [J]. 化工学报, 2014, 65 (4): 1344-1352. DOI: 10.3969/ j.issn.0438-1157.2014.04.026.
SONG P Y, HU X P, XU H J,. Effect of real gas on dynamic T-groove dry gas seal [J]. CIESC Journal, 2014, 65 (4): 1344-1352. DOI: 10.3969/j.issn.0438-1157.2014.04.026.

[7] 朱自强, 吴有庭. 化工热力学 [M]. 北京: 化学工业出版社, 2010: 126-147.
ZHU Z Q, WU Y T. Chemical Engineering Thermodynamics [M]. Beijing: Chemical Industry Press, 2010: 126-147.

[8] 李西平, 司云森.物理化学 [M]. 昆明: 云南大学出版社, 2006: 40-41.
LI X P, SI Y S. Physical Chemical [M]. Kunming: Yunnan University Press, 2006: 40-41.

[9] 王竹溪. 热力学 [M]. 2版. 北京: 北京大学出版社, 2014: 67-72.
WANG Z X. Thermodynamics [M].2nd ed. Beijing: Peking University Press, 2014: 67-72.

[10] PERRY R H. Perry’s Chemical Engineers’ Handbook [M]. 7th ed. New York: McGraw-Hill, 1997: 132-182.

[11] 陈钟秀, 顾燕飞, 胡望明. 化工热力学 [M]. 3版. 北京: 化学工业出版社, 2011: 184-185.
CHEN Z X, GU Y F, HU W M. Chemical Engineering Thermodynamics [M]. 3rd ed. Beijing: Chemical Industry Press, 2011: 184-185.

[12] 曾彪, 张旭, 鲍谦. 湿空气绝热节流系数计算及讨论 [J]. 暖通空调, 2011, 41 (9): 115-119.
ZENG B, ZHANG X, BAO Q,. Calculation and discussion of adiabatic throttling coefficient for moist air [J]. Heating Ventilating and Air Conditioning, 2011, 41 (9): 115-119.

[13] 马沛生, 宣爱国, 周彩荣，等. 化工热力学 [M]. 北京: 化学工业出版社, 2009: 40-42.
MA P S, XUAN A G, ZHOU C R,. Chemical Engineering Thermodynamics [M]. Beijing: Chemical Industry Press, 2009: 40-42.

[14] 程阳, 李东升, 胡佳成. 空气静压润滑焦耳-汤姆逊系数的计算方法 [J]. 润滑与密封, 2014, 39 (6): 103-107.
CHEN Y, LI D S, HU J C. The calculation method of Joule-Thomson coefficient in air aerostatic lubrication [J]. Lubrication Engineering, 2014, 39 (6): 103-107.

[15] 清华大学. 数学手册 [M]. 北京: 高等教育出版社, 2004: 88-89.
Tsinghua University. Mathematics Handbook [M]. Beijing: Higher Education Press, 2004: 88-89.

[16] 石玉冰. 真实气体等压热容的关联 [J]. 化肥设计, 2010, 48 (3): 11-13.
SHI Y B. Correlation of heat capacity at constant pressure for real gas [J].Chemical Fertilizer Design, 2010, 48 (3): 11-13.

[17] MATIN N S, HAGHIGHI B. Calculation of the Joule-Thomson inversion curves from cubic equation of state [J]. Fluid Equilibria, 2000, 175 (1): 273-284. DOI: 10.1016/S0378-3812(00)00443.

[18] WISNIAK J, AVRAHAM H. On the Joule-Thomson integral inversion curves [J]. Thermochimica Acta, 1996, 286 (1): 33-40.

[19] MAYTAL B Z, SHAVIT A. On the Joule-Thomson integral inversion curves of quantum gases [J]. Cryogenics, 1997, 37 (1): 33-38. DOI: 10. 1016/S0011-2275(96)00094 -X.

[20] COLINA C M, OLIVERA-FUENTS C. Prediction of the Joule-Thomson inversion curve of air from cubic equations of state [J]. Cryogenics, 1998, 8 (7): 721-728. DOI: 10.1016/S0011- 2275(98)00036-8.

[21] 刘延雷. 高压氢气快充温升控制及泄漏扩散规律研究 [D]. 杭州: 浙江大学, 2009.
LIU Y L. Investigating on control of temperature rise in fast filling of high pressure hydrogen and diffusion due to its leakage [D]. Hangzhou: Zhejiang University, 2009.

[22] 胡登辉. 非理想气体节流过程热力学研究及实践应用 [D]. 大庆: 东北石油大学, 2011.
HU D H. Non-ideal gas throttling process thermodynamic analysis and applied research [D]. Daqing: Northeast Petroleum University. 2011.

[23] 刘丰, 李晶晶. 基于HYSYS的焦耳-汤姆逊效应实验装置设计与模拟分析 [J]. 广州化工, 2014, 42 (14): 164-166.
LIU F, LI J J. Experimental design and simulation of Joule-Thomson effect based on HYSYS [J]. Guangzhou Chemical Industry, 2014, 42 (14): 164-166.

[24] 高光华, 童景山. 化工热力学 [M]. 北京: 清华大学出版社, 2007: 204-207.
GAO G H, TONG J S. Chemical Engineering Thermodynamics [M]. Beijing: Tsinghua University Press, 2009: 204-207.

[25] 马沛生, 夏淑倩, 夏清. 化工物性数据简明手册 [M]. 北京: 化学工业出版社, 2013: 17-18.
MA P S, XIA S Q, XIA Q. Chemical Property Data Concise Guide [M]. Beijing: Chemical Industry Press, 2013: 17-18.

[26] 郭天明. 多元汽-液平衡和精馏 [M]. 北京: 化学工业出版社, 2002: 161-300.
GUO T M. Diverse Vapor-Liquid Equilibrium and Distillation [M]. Beijing: Chemical Industry Press, 2002: 161-300.

[27] 李云, 姜培正. 过程流体机械 [M]. 2版. 北京: 化学工业出版社, 2008: 13-21.
LI Y, JIANG P Z. Process Fluid Machinery [M]. 2nd ed. Beijing: Chemical Industry Press, 2008: 13-21.

Analysis of Joule-Thomson effect of real gas system sealed by dry gas

DENG Chengxiang, SONG Pengyun, MA Ailin

(Faculty of Chemical Engineering, Kunming University of Science and Technology, Kunming 650500, Yunnan, China)

In a system sealed by dry gas, the Joule-Thomson (JT) effect occurs when the gas flows through the components of filters, valves, orifices and end faces, which may cause the temperature drop of sealing gas, even the appearance of liquid condensation. Generally, the Joule-Thomson effect is represented by Joule-Thomson coefficient. As to the hydrogen, nitrogen, air and carbon dioxide, which are often encountered for the cases of sealing by dry gas, the corresponding Joule-Thomson (JT) coefficients were calculated by four classical equations of state (EOS) of VDW, RK, SRK and PR. Subsequently, those calculated coefficients are compared with the experimental data in the literatures. The JT coefficient curves and Joule-Thomson inversion curves (JTIC) were plotted using the optimal equation of state. As to air and nitrogen through the end faces of dry sealing gas, the gas temperature drops caused by JT effect were calculated by applying the computer program. It shows that the Joule-Thomson effect of real gas, which have important influence on the throttle of dry sealing gas. At room temperature, hydrogen showed exothermic effect, while nitrogen, air and carbon dioxide endothermic (cooling) effect. The corresponding Joule-Thomson (JT) coefficients were calculated by the four classical EOS, the average relative error and maximum relative error of RK equation were the minimum, less than 4% and 10%, respectively. The JT effect of real gas causes large temperature difference in the dry sealing gas, of which the gas pressure more influences on the temperature drop than the gas temperature does. When the pressure is small, the temperature drop by the JT effect can be negligible.

dry gas seal; real gas; equation of state; Joule-Thomson coefficient; inversion curve

supported by the National Natural Science Foundation of China (51465026).

date: 2015-12-14.

Prof. SONG Pengyun, songpengyunkm@ ina.com

TB 42；TQ 031.1

A

0438—1157（2016）09—3833—10

10.11949/j.issn.0438-1157.20151892

国家自然科学基金项目(51465026)。

2015-12-14收到初稿，2016-06-23收到修改稿。

联系人：宋鹏云。第一作者：邓成香（1989—），男，硕士研究生。