基于随机Petri网的虚拟网可生存性模型研究

赵靓，邹宏，张校辉



基于随机Petri网的虚拟网可生存性模型研究

赵靓1，邹宏2，张校辉1

（1. 国家数字交换系统工程技术研究中心，河南郑州 450002；2. 国家网络空间安全发展创新中心，河南郑州 450000）

针对在描述可重构服务承载网(RSCN)差异化服务需求时无法定量描述其安全属性的问题，提出了一种RSCN可生存性模型。模型基于随机Petri网构建，首先构建RSCN的非马尔可夫随机Petri网模型，再基于最常用的先到先服务(FCFS)故障修复策略得到系统状态可达图，通过引入补充变量建立系统状态概率方程，并最终求解得到该模型。通过仿真实验对该可生存性模型的有效性进行验证，仿真结果表明，理论模型计算结果与仿真结果拟合性较好，可用于描述基于FCFS故障修复策略的RSCN可生存性能。

可重构服务承载网；可生存性模型；随机Petri网

1 引言

可重构柔性网络(CFN, configurable flexible network)理论[1,2]主要研究在实现网络资源高效利用的基础上如何面向用户的应用需求提供差异化网络服务。其中，可重构服务承载网[3~5]（RSCN, reconfigurable service carrying network）的相关研究内容就是以如何满足差异化服务需求为目标提出的。然而，现有相关研究在讨论RSCN承载的差异化服务时都是从业务属性出发进行描述的，重点在于为不同种类的服务提供所需的带宽等基础网络资源，以保障通信业务的基本需求得以满足，而对于其安全属性的需求则关注不足。事实上，差异化的安全属性也应是差异化服务需求的重要内容之一。例如，提供娱乐服务的承载网与提供金融服务的承载网在安全属性方面的需求显然是不同的。因此，在讨论RSCN如何提供差异化服务时不能仅考虑业务性能方面的需求，还必须充分考虑其安全性能的需求。

虽然目前还没有对网络安全性能衡量标准的定义，但在相关研究中，可生存性(survivability)作为一个重要的研究方向经常被提及。对于网络系统的可生存性较为认可的定义为：网络系统在遭受攻击、故障和意外事故的情况下及时完成任务的能力[6]。从其定义可以看出，网络可生存性与传统的网络安全性既有关联，又有较大的差异。传统的网络安全研究重点在于如何“防”，其目标是力争做到“事先能预防，事发能阻拦”；而可生存性技术的研究重点则是事后的识别和响应，旨在增强网络系统的免疫能力，即当攻击成功、系统已经被破坏时，如何修复系统，使其尽快恢复服务，从而减小损害。由此可见，在当下网络攻击频发、实时防御越来越困难的状况下，更应该加强网络可生存性研究，从而在理论上指导可生存系统的设计与实现，并有助于网络系统在复杂环境下的维护和技术改造。这与RSCN的设计理念非常贴近，因此，把可生存性作为RSCN安全性的一个重要评价指标。

信息系统可生存性研究的基础[7]是进行定量描述，因此本文以RSCN的可生存性模型的构建方法为主要研究内容，旨在为不同策略的系统提供一种准确评估其可生存性的方法。

2 相关工作

考虑到网络可生存性与安全性的相关性，可生存性定量分析方面的研究部分参考网络安全性的定量评价方法。传统的网络安全性定量分析有2种主要思路：1) 通过建立形式化的数学模型分析评价；2) 通过实验[8]来模拟分析网络系统及攻击行为，根据实验数据验证网络的安全性能。这2种方法对于研究如何防御网络攻击具有一定价值，但也存在较大局限，如较难应用于大规模系统的研究，特别是面对结构日益复杂的网络系统时，它们更加不适用。因此，1993年Littlewood等[9]在网络安全性评价中引入系统可信赖性的分析方法，并取得一定效果。

网络可生存性定量分析除了借鉴网络安全性定量分析方法外，还在攻击模型的基础上基于图论和随机模型进行分析。文献[10]利用模型检测技术生成系统情景图，给节点赋予入侵及失效的时间概率分布，采用贝叶斯网络描述有依赖关系节点的概率值，由此计算网络的可用性。文献[11]假设系统失效时间的随机分布，从而得到网络的马尔可夫模型，由此评价可用性指标，该方法提供了网络可生存性评价的一般框架。文献[12]计算了简单环形网络和一般网络的可生存性，该方法通过对实际网络的定期采样获得网络节点的失效概率，并以该条件概率定义网络系统的可生存性函数。文献[13]抽象并获得网络安全的状态转移，假定所有状态的停留时间是指数分布，通过求解相应的马尔可夫链得到网络系统的平稳概率分布，进而分析网络的可生存性。文献[14]提出一种面向对象的软件系统的生存性模型，文献[15]提供一种随机模型框架和相关计算技术，文献[16]基于包括免疫评估算法在内的评估计算给出一种网络生存性评估模型。

从上述关于网络可生存性定量评价的工作来看，对于网络可生存性定量评价，目前主要采用的方法大部分是基于随机模型的分析方法，说明该方法在网络性能评价方面已经得到广泛认可，根据该方法得到的性能模型能够较准确地反应系统的性能指标，但是上述研究均没有说明如何得到一个准确的随机模型。另一方面来看，上述的评价模型大多停留在验证系统是否满足某些抗毁性特征上，而对于系统故障恢复方面的描述能力不足。而可重构网路在网络故障恢复方面具有显著的优势，如果直接套用上述随机模型则无法准确描述其故障恢复的特征，这种情况下往往得到可生存性指标偏差较大，对具体的可重构网络系统的可生存性判断不够准确，很难指导新的可重构服务承载网的构建，因此本文引入基于随机Petri网[6]的建模方法，构建适用于描述RSCN系统生存性的模型，用于评估和指导构建RSCN系统。

3 RSCN的可生存性评价指标

不同的评价体系其评价指标也不同，目前对于网络可生存性能就存在很多评价指标，而可用性则是业界最为认可的，也是最重要的可生存性评价指标，该指标用于量化网络系统有效和无效的变化。一个RSCN系统，可以根据安全等级需求定义其失效的临界条件，若达到临界条件阈值则认为系统失去服务能力，变为失效系统。由此，本文将系统稳态可用性作为RSCN可生存性的主要评价指标，用以描述RSCN系统的可生存性能。

一般来说，网络可用性分析中通常假设完全可靠的是网络节点，不可靠的只是链路。而在遭受恶意攻击的情况下，一般节点才是攻击目标，而非链路。基于上述分析，本文在计算系统可用性时假设节点不可靠，遭到攻击后会发生故障失效，但RSCN系统中的节点或链路发生故障后，能够通过故障修复机制进行修复。基于该假设条件，定义和形式化描述RSCN系统可用性。

定义2 （系统失效因子） RSCN中的链路数为，如果其中的任意条链路同时故障，系统即变为失效系统，则该条件为系统失效的临界条件，此时故障链路数与链路总数的比率称为RSCN系统失效因子，记为。

根据上述定义，一个RSCN系统，若节点数为，链路数为系统失效因子为，则系统失效条件为同时失效的链路数不小于。假定RSCN的节点平均链接度为，则根据定义1可知一个节点失效，相应会有条链路失效。由此，RSCN系统失效的临界条件也可表示为个节点同时失效。

定义3 （RSCN稳态可用性）成功构建且长期运行的RSCN网络系统，系统有效运行的时间与总运行时间的比值称为系统稳态可用性。稳态可用性也可表示为系统处于有效状态的稳定概率之和，描述为

4 RSCN的随机Petri网模型

4.1 随机Petri网及其在可靠性分析中的应用

Petri网是一种图形化和形式化的建模工具，最早于1962年由Carl Adam Petri在“用自动机通信”中提出。他使用网状结构模拟通信系统，包括条件和事件2类节点，在条件和事件为节点的有向二分图的基础上加上标识状态信息的托肯（Token）分布，并按一定的引发规则使事件驱动状态演变，从而反映系统的动态运行过程。

图1所示为一个简单的Petri网。用*和*分别表示的前置集和后置集，为Petri网的一个标识。则初始标识，，等。：，其中，变迁和在标识处于并发关系，而变迁和在标识处于冲突关系。该Petri网的可达标识集合为={,,,,,}，因此该Petri网的状态图如图2所示。

随机Petri网（SPN, stochastic Petri net）最早由Shadiros提出，其基本思想是：对每一个变迁，从其被激活开始到执行的时间是一个连续的随机，可以具有不同的分布。用随机Petri网对动态系统性能评估、分析和模拟，实质上是给出离散随机过程的一个图形化描述。

本文在RSCN系统的可靠性模型建立过程中引入这种适合于复杂系统可靠性分析的方法，用以构建本文中的RSCN状态模型。

4.2 RSCN可用性建模分析

RSCN是由链路及相互独立的节点构成的复杂系统，其中的链路及节点故障可以修复，根据不同的可重构故障修复机制其修复时间可能存在差异，但不影响RSCN成为一个可修复系统。因此，基于可修复系统的建模方法可以对RSCN进行系统性能分析及建模。

马尔可夫可修复系统的定义为：系统中部件相互独立，其寿命及修复时间均服从指数分布的系统。这类系统的状态可由一个时齐马尔可夫链来描述。对于这类可修复系统进行性能分析，即要得到系统稳态可用性，较为成熟的方法是建立系统的运行状态集及故障情形下各状态之间的转移关系，然后通过马尔可夫过程得到稳态概率分布。但是对于RSCN这样的复杂系统来说，所有可达状态的直接求解不但繁琐，而且非常容易出错，因此必须寻求其他的求解方法。由于已经证明SPN的状态可达图同构于一个齐次马尔可夫链，因此可以通过建立可修系统的SPN模型即可获得系统的状态可达图，随即就可利用马尔可夫理论对可修系统的性能进行定量分析。主要方法为：将SPN的每个标识映射成马尔可夫链(MC, Markov chain)的一个状态，SPN的可达图即可与一个MC的状态空间同构，由此获得MC转移概率矩阵参数，再通过计算得到MC每个状态稳定状态概率，即可得到各种性能指标。

在上述SPN中，对应于各变迁的分布函数都是一个指数分布函数，而指数分布引发的延迟具有无记忆特性，因此SPN系统可达图与连续时间马尔可夫过程同构。基于上述分析，通过建立系统的SPN模型，得到系统状态可达图，然后再利用马尔可夫理论即可对服从指数分布的系统进行性能分析。

由于RSCN中发生的攻击和入侵具有不确定性，因此假定其寿命服从指数分布是合理的；同时假定攻击发生后节点或链路出现故障，由于该系统是可修复系统，因此上述故障都是可修复的，但是基于不同的故障修复算法其修复时间不同，而故障修复算法是与系统决策及当前的网络状态紧密相关的，因此RSCN系统中的故障修复时间不服从指数分布。对类似上述这样寿命或修复时间不服从指数分布的可修复系统，由于其马尔可夫性被破坏，所以对RSCN系统进行性能分析时不能直接运用SPN模型。此时需要用到非马尔可夫随机Petri网（NMSPN, non-Markovian stochastic Petri net）。NMSPN不具有马尔可夫性，允许指数变迁、瞬时变迁以及一般变迁共存，这正好满足RSCN修复时间不服从指数分布这一特点，因此考虑基于NMSPN进行RSCN可靠性建模。若系统中有可实施的瞬时变迁，需要先把消失状态移出，得到化简的随机过程。对此进行分析求解时可以利用马尔可夫再生理论或补充变量法。基于上述分析，本文通过构建NMSPN模型进行RSCN可靠性建模。

4.3 NMSPN模型构建

假设一个RSCN的节点数为，链路数为，系统失效因子为且RSCN中所有资源都由系统维护中心（SMC, system maintenance center）进行维护，一旦发生故障也由SMC进行探测及修复。假设该系统的链路寿命和节点寿命分别是服从参数为和的指数分布，当其中任何链路或节点故障并失效时，由SMC进行探测、管理和修复等处理。故障时若遇空闲的SMC，链路或节点故障会立即被处理；否则，链路或节点故障必须排队等待处理，直到当前正在进行的故障修复任务被SMC完成。为模型简化，文中后续仅描述节点故障情况。

假设RSCN中链路和节点的故障修复所需的时间服从一般分布，分布函数分别为和，分布密度函数分别为和，该条件下RSCN的NMSPN模型如图3所示。

5 RSCN状态可达图

5.1 故障修复策略

RSCN中可以采取不同的故障修复策略应对RSCN中发生的故障，基于不同的故障修复策略会得到不同的状态可达图，从而也会生成不同的RSCN系统性能模型。故障修复策略事实上亦是一种调度策略，在各类调度的策略中，FCFS总是被优先提及并被广泛应用的策略，主要原因为：1）FCFS策略易于实现；2）调度公平性较好。因此本文以先来先服务策略（FCFS, first-come first-served）为例构建RSCN可靠性模型，并举一反三的说明各种可靠性模型的建立方法。

FCFS策略是SMC用以处理多个可能同时到达的RSCN故障的应对方法，它总是先处理最先到达的故障。如图4中位置中的托肯表示需要处理的故障，当数量超过1时，由于只能有一个托肯进入位置进行修复处理，因此其他故障必须按照到达的先后顺序在位置排队等待，位置中的故障处理完成后，从位置的队头中取一个托肯进行修复处理，直到位置中的队列为空为止。

5.2 基于FCFS修复策略的RSCN状态可达图

设RSCN系统中的节点数量为如果采用FCFS故障修复策略，根据4.3节的NMSPN模型，经移除消失状态后由图4所示模型可得到如图5所示的状态可达图。该状态可达图中的状态编号分别表示故障节点的数量，即状态0表示无故障节点的状态，状态1表示故障节点为1个的状态，以此类推，状态为全部节点故障的状态，故而该状态可达图中共有1个状态。

根据分析可知RSCN状态可达图的规模与节点数量强相关，因此为了简化后续描述及推导过程，下面描述的系统可达图及由此推导性能模型均假定节点数量为5、链路数量为7，并且RSCN系统失效因子。

由于故障节点在时刻开始到修复完成所需要的时间会影响系统状态的变化规律，所以将补充变量引入到系统性能模型中。引入的变量表示正在被处理的故障节点已经花费的时间，则得到节点故障的修复速率函数为

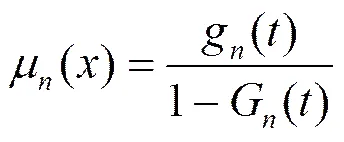
6 RSCN的性能评价模型

本文在求解RSCN系统的各种性能指标时，主要从系统性能下降的可控性和系统可用性角度来评价RSCN系统可生存性性能，因此在基于上述状态可达图求解过程中，侧重于针对系统可用性给出评价模型，从而通过可用性指标对系统性能进行描述。

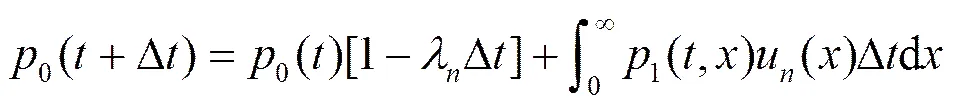
(4)

(5)

(7)

(8)

约束条件为

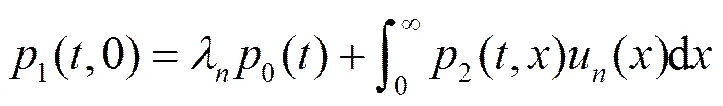
(10)

(11)

(13)

对上述方程进行求解（求解过程略），可得到5节点RSCN系统基于FCFS策略的各可达状态概率分布函数分别为

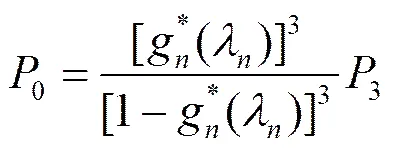
(15)

(16)

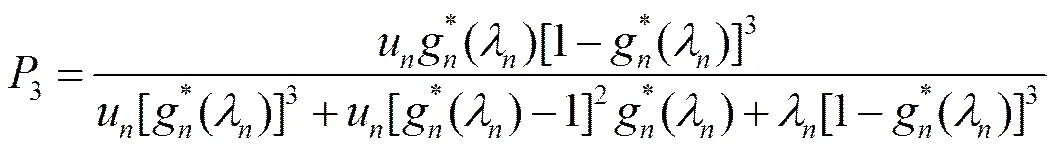
(18)

(19)

根据式（1），基于FCFS策略的RSCN系统稳态可用性是可用状态的概率求和，由5.2节分析可知，对于失效因子，节点数为5、链路为7的网络，和状态为有效状态，所以该网络的稳态可用性可表示为

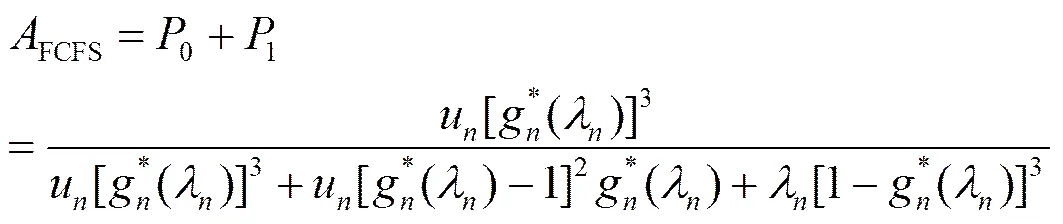
7 实验及仿真分析

7.1 实验环境

实验在Intel(R) Core(TM) i7 CPU 2.67 GHz，RAM 2 GB的PC上进行，虚拟网络的的拓扑变化通过C++编程仿真实现，同时模拟构建及撤销RSCN。

1) 物理网络：引入GT-ITM[17]。工具生成底层的物理网络拓扑，模拟的物理网络的节点数是50，且任意节点间存在链路的概率是25%，由此计算可得初始网络拓扑中存在的物理链路数是300，虚拟网络的链路和节点资源服从均匀分布，且取值为[50, 100]。

2) 服务承载网：假设在上述物理网络中有20个具有随机拓扑结构的服务承载网，且链路资源请求在[5, 30]内均匀分布；节点数也服从均匀分布，取值为[2, 8]。

在上述实验环境中，模拟故障修复，且采用FCFS策略。实验过程中，链路和节点的可靠性初始值均为1，寿命都服从指数分布，且节点失效率；单个节点故障的修复时间服从均值的伽玛分布。

7.2 系统性能分析

1) 模型计算的结果与实验验证结果的拟合性很好，证明本文分析所得的系统可用性模型准确性较高，从而也证明提出的构建系统可用性模型的方法正确。

2) RSCN的性能受到故障修复平均时间的极大影响。如图7所示，故障修复时间越短，RSCN的性能越好，反之亦然。所以当故障率水平稳定时，如果通过研究故障修复技术缩短故障修复时间，则可有效控制整个RSCN系统可用性。

3) RSCN的性能与故障间隔平均时间关系紧密。如图8所示，故障间隔的时间越短，RSCN的性能越差，反之亦然。故而若故障修复平均时间确定，如果通过研究防故障技术有效增大故障发生的频率，则可提升整个RSCN系统可用性。

4) 系统可用性还受到网络规模的影响。如图7和图8所示，实验1和实验2分别对应不同规模网络，其中，实验1比实验2的网络规模小，由仿真图分析可知对于不同规模的网络，其故障间隔时间和故障修复时间对系统可用性的影响趋势是一致的，但是其影响量化值具有差别。

通过对RSCN系统可用性与各参数的关系对比分析，故障发生频率与故障修复时间都对系统性能产生较大影响，若要进行系统性能控制应研究故障快速修复技术和防故障技术。

8 结束语

本文主要针对网络系统可生存性性能进行建模分析。基于SPN构建复杂系统可靠性模型的方法构建出了RSCN的SPN模型，并基于FCFS故障修复策略构建了相应的状态可达图，然后通过马尔可夫随机过程的分析方法构建了系统可生存性模型。

基于模型分析和实验验证，指出这2种可以提升网络性能的关键技术，即故障修复技术和网络防故障技术。其中，故障修复技术研究的主要目标是提升RSCN的故障修复速度，缩短故障修复时间；网络防故障技术研究的主要目标是通过防故障技术的应用，减小网络节点及链路受攻击而发生故障的速率，这些均为后续相关研究提供了理论基础。

[1] 程东年, 汪斌强,等. 网络结构自调整的柔性内涵初探[J]. 通信学报, 2012 , 33(8): 214-222.

CHENG D N, WANG B Q, et al. Preliminary study on the connotation of flexibility in dynamically reconfigurable networks[J]. Journal on Communications, 2012, 33(8): 214-222.

[2] 兰巨龙, 邢池强, 胡宇翔, 等. 可重构技术与未来网络体系架构[J]. 电信科学, 2012, 29(8): 16-23.

LAN J L, XING C Q, HU Y X, et al. Reconfiguration technology and future network architecture[J]. Telecommunications Science, 2012, 29(8): 16-23.

[3] 齐宁, 汪斌强, 王志明. 可重构服务承载网容错构建算法研究[J]. 电子与信息学报, 2012, 34 (2): 468-473.

QI N, WANG B Q, WANG Z M. Research on reconfigurable service carrying network resilient construction algorithms[J]. Journal of Electronics & Information Technology, 2012, 34(2): 468-473.

[4] 王志明, 汪斌强. 基于备份的可重构服务承载网可靠性映射方法[J].电子与信息学报, 2013, 35(1): 126-132.

WANG Z M, WANG B Q. Reliable mapping method for reconfigurable service carrying netwok based on path backup[J]. Journal of Electronics & Information Technology, 2013, 35(1): 126-132.

[5] 张博, 汪斌强, 袁博. 面向可重构服务承载网的分域混合承载组调度研究[J]. 电子与信息学报, 2012, 34(5): 1231-1238.

ZHANG B, WANG B Q, YUAN B. Research on partition domain hybrid carrying group scheduling based on reconfigurable service carrying network[J]. Journal of Electronics & Information Technology, 2012, 34(5): 1231-1238.

[6] ELLISION R J, FISHER D A, LINGER R C, et al. Survivable network systems: an emerging discipline [R]. Carnegie Mellon University, 1999.

[7] WESTMARK V R. A definition for information system survivability[C]//The 37th Internal Conference on System Sciences. Hawaii, USA, c2004: 127-136.

[8] 卢山. 网络生存性评估模型的仿真分析[J]. 计算机仿真, 2013, (9): 270-273.

LU S. Simulation analysis of network survivability assessment model[J]. Computer Simulation, 2013, (9):270-273.

[9] LITTLEWOOD B, BROCKLEHURST S, FENTON N, et al. Towards operational measures of computer security[J]. Computer Security, 1993, 2(2/3):211-230.

[10] LANDWEHR C. Formal models for computer security[J]. Computer Surveys, 1981,13(3):247-278.

[11] LIEW S C, LU K W. A framework for characterizing disaster-based network survivability[J]. IEEE Journal on Selected Areas in Communications, 1994, 12(1):52-58.

[12] JHA S, WING J, LINGER R, et al. Survivability analysis of network specifications[C]//International Conference on Dependable Systems and Networks(DSN). New York, USA, c2000: 613-622.

[13] LIU Y, TRIVEDI K S. A general framework for network survivability quantification[C]//The 12th GI/ITG Conf Measuring, Modeling and Evaluation of Computer and Comm. Systems(MMB) together with Thid Polish-German Teletraffic Symposium(PGTS). Dresdes, Germany, c2004: 369-378.

[14] SODIYA A S, ABORISADE D O, IKUOMOLA A J. A survivability model for object-oriented software systems[C]//Computational Aspects of Social Networdk(CASoN). Sao Carlos, c2012: 283-290.

[15] XIE L, JIANG Y M, HEEGAARD P E. Modelling and analysis of the survivability of telecommunication networks[C]//Performance Evaluation of Computer and Telecommunication Systems(SPECTS). Toronto, c2013:91-98.

[16] WANG C L, FANG L, DAI Y Q, et al. Network survivability evaluation model based on immune evolution and multiple criteria decision making[C]//Cyber-Enabled Distributed Computing and Knowledge Discovery(CyberC). Sanya, China, c2012: 178-184.

[17] 原菊梅. 复杂系统可靠性Petri网建模及其智能分析方法[M]. 北京: 国防工业出版社, 2011.42-64.

YUAN J M. Reliability Petri net modeling of complex systems and intelligent analysis[M]. Beijing: Defense Industry Press, 2011.42-64.

Survivability model for reconfigurable service carrying network based on the stochastic Petri net

ZHAO Liang1, ZOU Hong2, ZHANG Xiao-hui1

(1. National Digital Switching System Engineering and Technology Research Center, Zhengzhou 450002, China; 2. National Cyberspace Security Development Innovation Center, Zhengzhou 450000, China)

Aiming at the defect that the security attribute of RSCN couldn’t be described with measurement, a survivability model for RSCN was proposed based on the stochastic Petri net. Firstly, a non-Markovian stochastic Petri net for RSCN was proposed, and then the state schematics was educed based on the FCFS fault repair policy subsequently. Finaly, the survivability model was concluded based on the probability equation of system state by importing supplementary variable. The model was analyzed and validated for validity through emulational experiments. The emulational results show that the comparability between the computed-results of model and emulational results is good, and the model can be used to discribe the survivability for RSCN.

reconfigurable service carrying network, survivability model, stochastic Petri net

TP393

A

10.11959/j.issn.1000-436x.2016054

2015-01-14；

2015-04-17

国家高技术研究发展计划（“863”计划）基金资助项目(No. 2015AA016102)；国家重点基础研究发展计划（“973”计划）基金资助项目(No.2012CB315905)；国家科技支撑计划基金资助项目(No.2012BAH02B01)

The National High Technology Research and Development Program of China (863 Program) (No. 2015AA016102), The National Basic Research Program of China(973 Program)(No. 2012CB315905), The National Science and Technology Support Program (No. 2012BAH02B01)

赵靓（1979-），女，山西盂县人，博士，国家数字交换系统工程技术研究中心工程师、讲师，主要研究方向为新一代信息网络关键技术与理论、可重构网络安全等。

邹宏（1976-），男，天津人，国家网络空间安全发展创新中心工程师，主要研究方向为计算机应用技术。

张校辉（1979-），男，河南洛阳人，博士，国家数字交换系统工程技术研究中心工程师、讲师，主要研究方向为SDN。