基于互信息的分散式动态PCA故障检测方法
童楚东,蓝艇,史旭华
基于互信息的分散式动态PCA故障检测方法
童楚东,蓝艇,史旭华
(宁波大学信息科学与工程学院,浙江宁波 315211)
对现代大型复杂动态过程来讲,不同测量变量会存在不同的序列相关性,而且变量间的相互影响会体现在不同的采样时刻上。为此,结合利用分散式建模的优势,提出一种基于互信息的分散式动态过程故障检测方法。该方法在对每个测量变量都引入多个延时测量值后,利用互信息为每个变量区分出与其相关的测量值,并建立起相应的变量子块。这种变量分块方式使每个变量子块都能充分地获取与之相对应的自相关性与交叉相关性信息,较好地处理了数据的动态性问题。然后,利用主元分析(PCA)算法对每一变量子块进行统计建模从而建立起适于大规模动态过程的多模块化的故障检测模型。最后,通过实例验证该方法用于动态过程监测的可行性和有效性。
主元分析;过程系统;互信息;故障检测;统计过程监测
引 言
近年来,数据驱动的故障检测方法因其简单通用性,已作为保障生产安全的重要技术手段而得到了研究者们的重视[1-2]。针对以主元分析(principal component analysis,PCA)为代表的多变量统计过程监测方法的研究已经受到了工业界和学术界的广泛关注,其基本思想都是从工业过程采集的数据中挖掘出能反映过程运行状况的潜在信息[3-4]。这类方法能避免建立精确的过程机理模型,因而很适合于监测现代大型复杂化工业过程。
通常来讲,传统的PCA故障检测模型假设过程变量满足独立同分布,即要求测量变量序列不相关。但现代复杂工业过程由于广泛采纳先进计算机与DCS技术,采样数据间不可避免地存在序列相关性,即存在动态特性。为解决这一动态过程故障检测问题,Ku等[5]提出先在过程数据矩阵中引入延时测量值构成增广矩阵后再对其进行PCA建模,这也就是动态PCA(dynamic PCA,DPCA)及其他类似方法的基本出发点[5-6]。Kerkhof等[7]结合利用自回归模型与偏最小二乘回归算法来消除数据自相关性与交叉相关性的影响,解决了间歇动态过程监测问题。Li等[8]通过在数据投影变换的过程中区分过程数据的自相关性和交叉相关性,使提取的数据动态潜隐成分(dynamic latent variables,DLV)具有很好的可解释性,进而提出了一种基于DLV算法的动态过程故障检测方法。然而,考虑到现代工业过程数据的复杂性,不同测量变量会存在不同的自相关性,而且变量间的相互影响(即交叉相关性)会体现在不同的采样时刻上。因此,动态过程故障检测问题还有待进一步深入研究。
此外,工业过程规模的大型化发展趋势已逐步凸显出单个集中的故障检测模型的局限性,分散式故障检测方法更适合于处理大规模工业过程监测问题。Zhang等[9-10]详细研究了针对大型过程的分散式故障检测策略,提出了多种多模块化的监测思路。可是,这类基于多模块化算法的分散式故障检测模型需要以过程机理和生产结构等知识为前提对测量变量做多分块化处理。可想而知,若先验知识不充分,就无法建立分散式的多块故障检测模型。为此,有学者提出完全从数据统计特性角度出发的变量分块方法,在不需要任何机理知识的前提下实现了基于纯数据的分散式故障检测[11-13]。无可否认,分散式建模方法在进行分块化处理的过程中能降低过程数据分析的复杂度,在监测大型工业过程对象时常表现出优越的性能。然而,在这些方法中,前面所提及的过程数据的动态性问题却未得到充分的研究。
本文针对前述动态过程故障检测与分散 式建模的不足,提出一种基于互信息(mutual information,MI)的分散式动态PCA建模方法并将其应用于工业过程故障检测。在信息论领域里,互信息常用来度量一个随机变量中包含的另一个随机变量的信息量[14]。MI的这种度量相关性的方式不局限于单纯的线性关系,对变量之间的非线性关系也能进行评估[15]。本文首先对每个测量变量都引入多个延时测量值,然后针对每个测量变量,利用互信息区分出与其相关的测量值并建立起相应的变量子块。最后,对每一变量子块进行PCA建模从而建立起适于大规模动态过程的多模块化的故障检测模型。基于MI-DPCA方法的有效性与优越性将在标准Tennessee Eastmann(TE)[16]仿真实验平台上通过对比分析进行验证。
1 基本方法
1.1 PCA与DPCA
PCA算法旨在提取相互正交的主元以摒除原始数据空间的冗余信息而保留大量的方差信息[3]。通过对经过标准化处理后的数据矩阵(为样本数,为变量数)进行奇异值分解,可建立PCA统计模型,即[1]
若是考虑过程数据序列相关性,可对引入前个时刻的测量值,构成如下增广型矩阵[5]
1.2 互信息
互信息(MI)是信息论里一种无参数、非线性的测度指标,它可以用来评估两个测量变量间的相关性。目前,多变量统计过程监测领域也有一些借鉴互信息分析处理过程数据的研究成果[17-18]。设两个随机变量和的联合分布为,边缘概率分别为和,互信息则定义为
若和之间不存在重叠的信息,即相互独立时,互信息值等于0。反之,若两者间的相关性越高,互信息值越大。值得注意的是,求解需要已知各变量的分布密度概率,实际应用中通常是使用核密度估计方法来确定对应的概率值。
2 基于MI-DPCA的过程监测方法
2.1 基于MI分散式动态过程建模方法
考虑到复杂动态过程变量间的相关性交错,不同测量变量会存在不同的序列相关性,而且变量间的相互影响会体现在不同的采样时刻上。为了更好地描述每个测量变量的动态性,提出如图1所示变量分块方法。具体的实施步骤介绍如下。
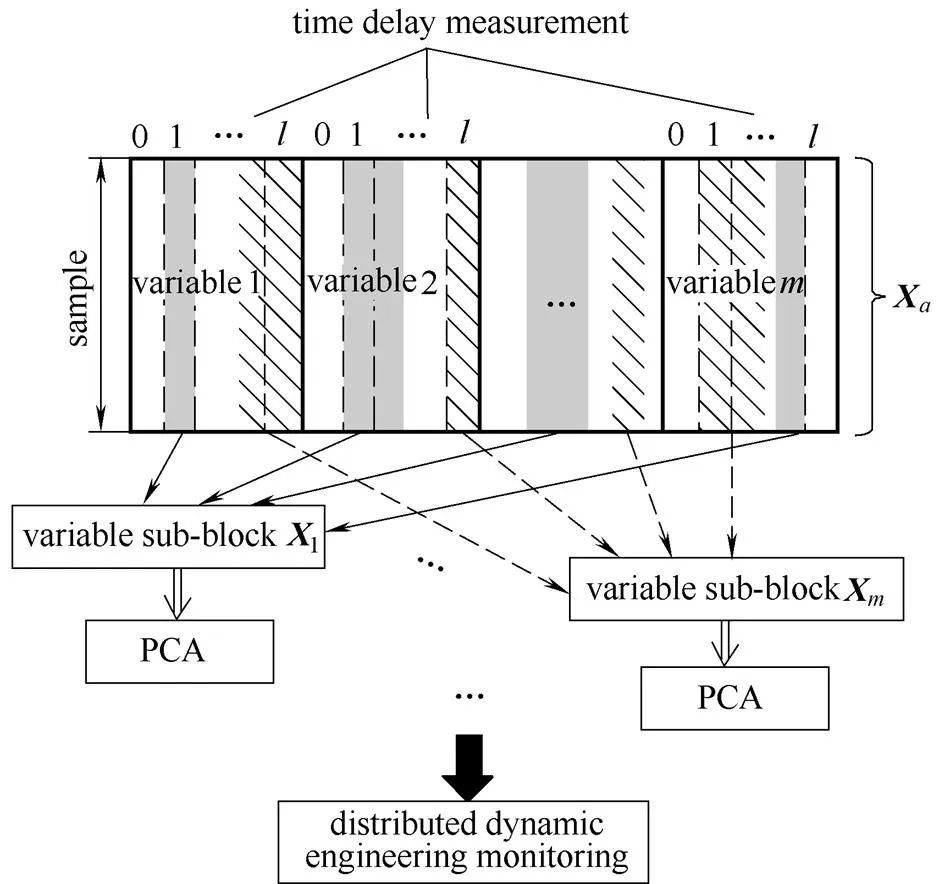
图1 基于MI的变量分块方法
(1)为每个变量引入个时刻的测量值构成增广型数据矩阵;
(4)对所得到个变量子块分别建立基于PCA算法的故障检测模型,即
从上述步骤中可知,每个子块中包含的变量是最能用来描述相应测量变量的动态性。与DPCA直接用所有个变量进行分析相比,本文所涉及的变量选择方法能剔除某些不相关变量的“干扰”影响,从而使子块PCA模型更好地反映出每个测量变量的动态性特征。因此,MI-DPCA方法在监测动态过程运行状况时理应能取得更优越的故障检测效果。
2.2 基于MI-DPCA模型的过程监测方法
值得指出的是,相比于DPCA与DLV方法,MI-DPCA方法因使用互信息与分散式建模方法而导致其计算量有所增加。然而,互信息与分散式PCA模型都是在离线建模阶段进行的,不会对在线故障检测直接产生影响。另外,基于贝叶斯推理的在线故障监测指标的概率融合只涉及简单的数学计算,在计算机处理器飞速发展的今天,所增加的在线计算量几乎可以忽略不计。
3 仿真实验研究
TE仿真模型因其反应过程和生产结构的复杂性,已经成为测试不同控制方法和过程监测策略的标准实验平台[20-22]。TE过程的流程如图2所示,主要由连续搅拌反应器、产品冷凝器、气液分离塔、汽提塔和离心式压缩机5个生产单元组成。TE过程可连续测量22个过程变量和12个操作变量,还可以仿真模拟如表1所列的21种不同的故障类型,详细资料可见文献[16]。在本文的研究中,选取过程可连续测量的33个变量作为监测变量,详情可见文献[11]。过程的测试数据可从网站http://web.mit. edu/braatzgroup/links. html上下载,所有的故障测试数据集都是从160个采样时刻后引入非正常工况。

图2 TE过程结构
离线建模阶段,利用正常工况下的960个样本建立DPCA、DLV[8]和MI-DPCA的过程监测模型以作对比分析用,置信限统一取值99%。其中,DLV故障检测模型采用的是3个监测统计量,、以及Q,分别用于监测动态潜隐成分、静态潜隐成分以及残差。除此之外,相应的模型参数设置与原始文献[8]一致,有关DLV的详细介绍可见文献[8],这里不再赘述。按照Ku等[5]提出的方法,在DPCA与MI-DPCA模型中,确定引入的延时测量值个数,保留的主元个数通过累计方差贡献率(CPV≥85%)准则求得。而在MI-DPCA模型中,同样引入个延时测量值,每个子块中选择的变量个数,且每个子块PCA模型中的主元个数都通过CPV≥85%准则进行设置。
首先,将3种故障检测模型用于监测TE过程21种故障工况,并计算针对每种故障监测的故障漏报率,详情列于表1中。值得注意的是,故障3、9和15由于对过程的影响甚微,很多文献都证实这3种故障是很难被有效地检测出来的[8,21]。因此,在本研究中不予考虑。在表1中,取得最小漏报率的监测指标已用黑体标出。显而易见,MI-DPCA方法在绝大多数故障类型上能取得优越于传统DPCA以及DLV方法的故障检测结果。尤其是针对故障10与16,故障漏报率得到大幅度下降。这主要是因为MI-DPCA方法为每个测量变量选择与之相关的不同延时测量值,极大地遏制了不相关测量值的负面影响。因此,所建立的子块PCA模型能更好地描述相应测量变量的动态性特征,降低了故障漏报的可能性。为了更好地体现MI-DPCA相对于DPCA与DLV方法的优越性,特将故障16的过程监测图显示于图3中。从图中可以较直观地看出3种方法在监测故障16时的漏报情况。此外,虽然MI-DPCA方法未能在故障1、2、和19上取得最佳监测效果,但是相应的漏报率值相差微乎其微。值得指出的是,针对故障5,MI-DPCA方法的故障检测率明显低于DLV方法,但从图4中的监测结果来看,两者都能在第一时间触发故障警报并持续一段时间。从工程实践角度来看,这不会影响MI-DPCA方法针对故障5的监测效果。
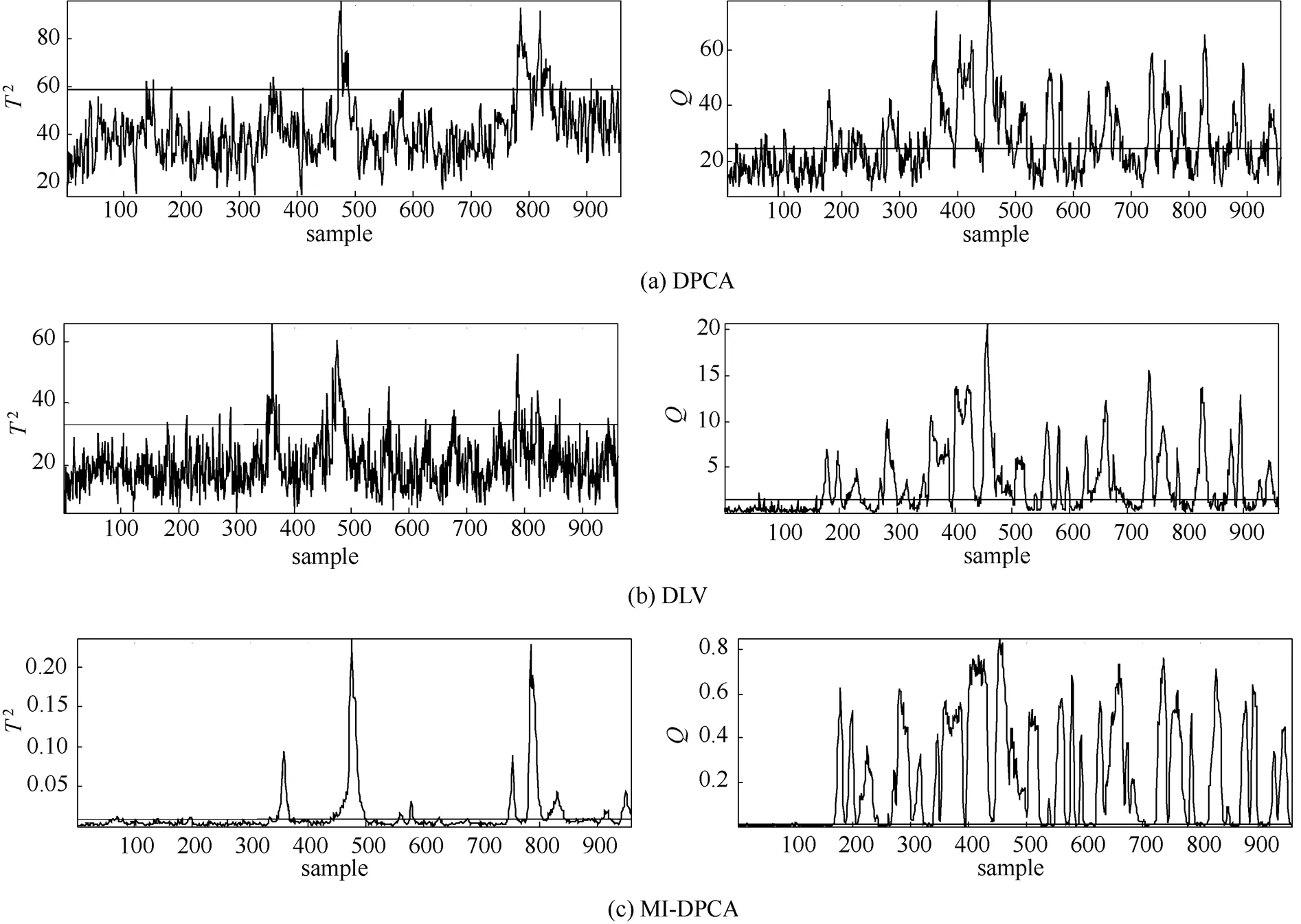
图3 故障16的过程监测结果
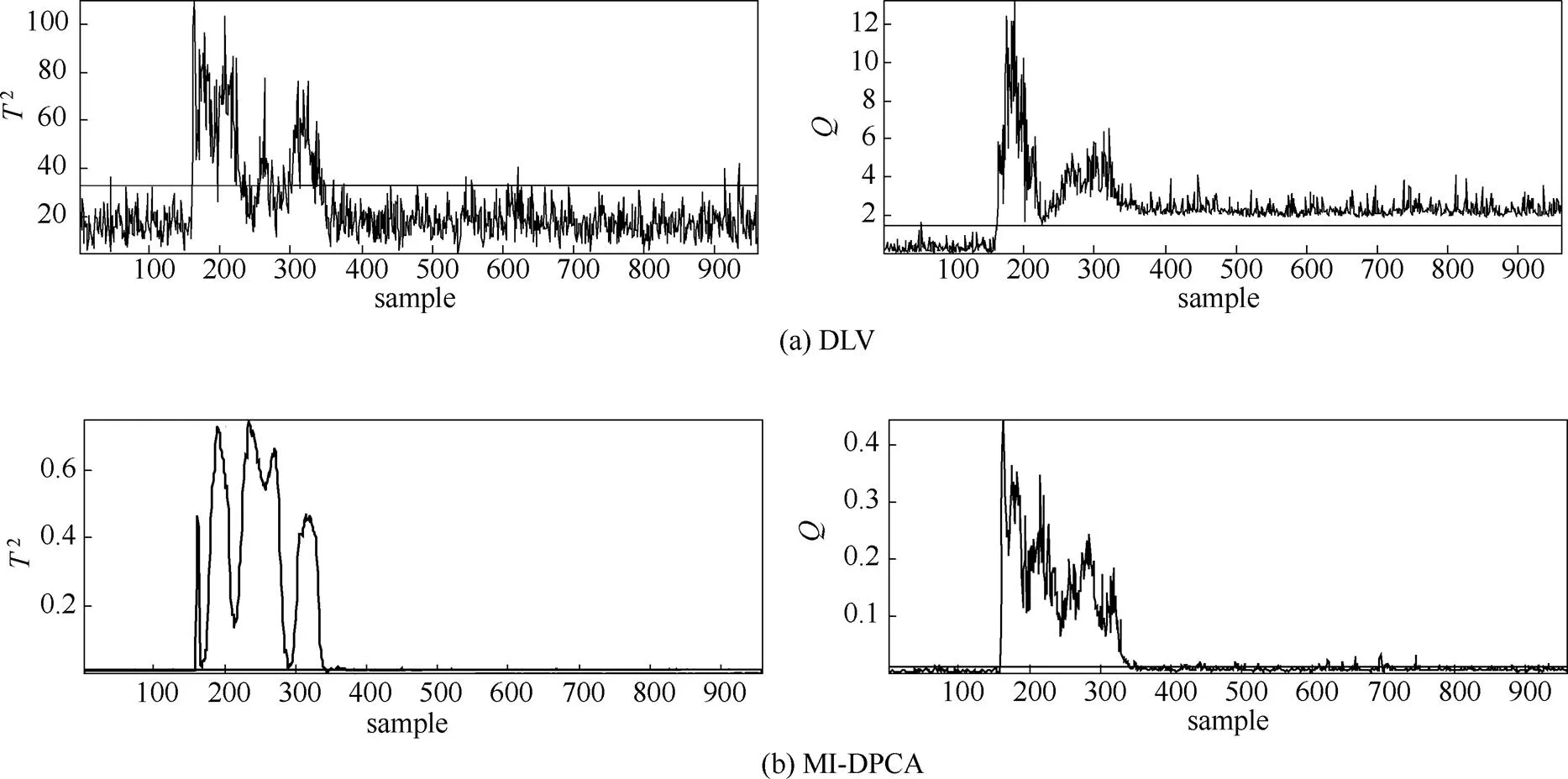
图4 故障5的过程监测结果
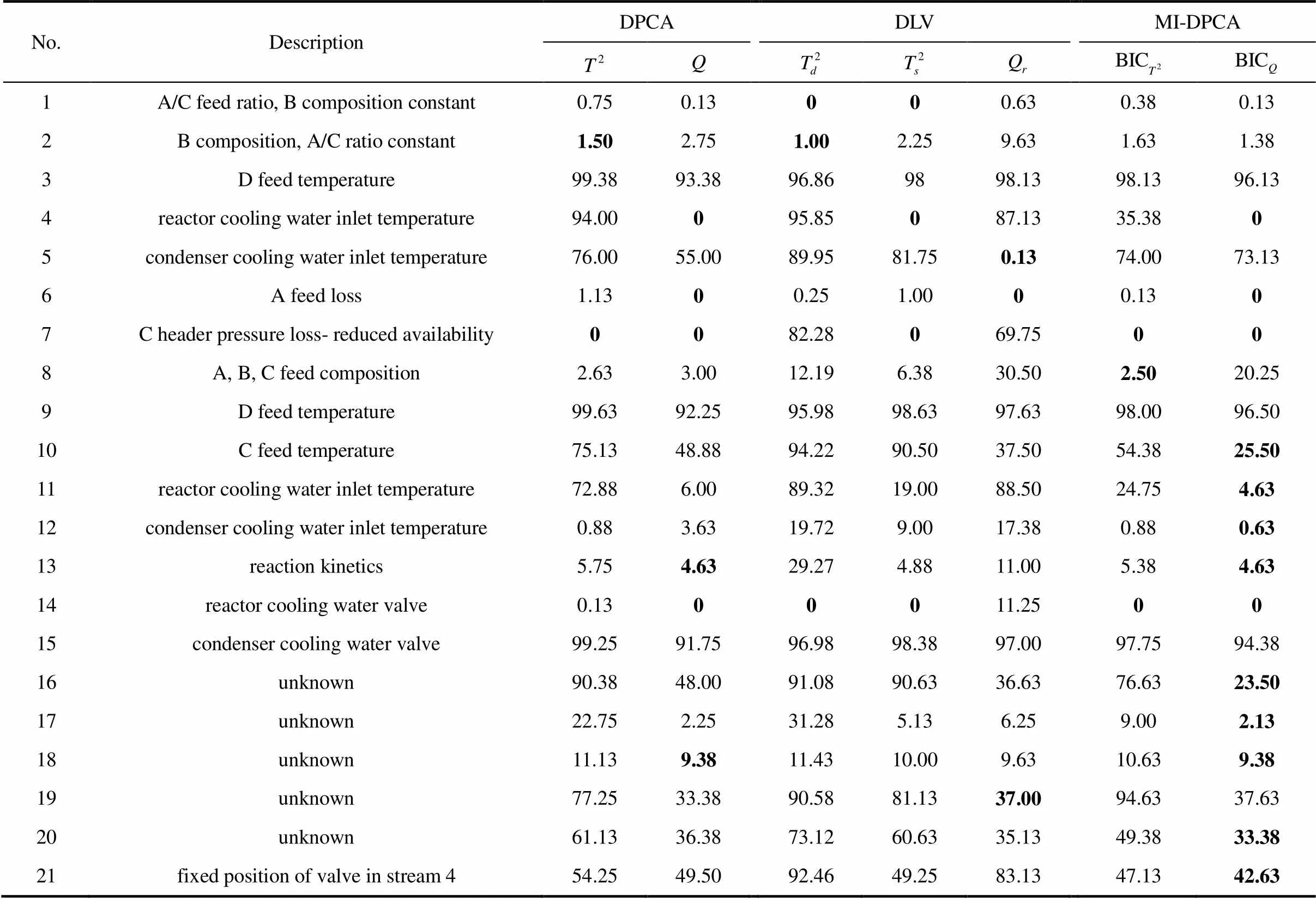
表1 TE过程故障漏报率
其次,为进一步说明MI-DPCA方法的有效性,还需对比分析3种方法的故障误报率,即将正常数据样本错误的判别为故障。通常来讲,较低的故障漏报率会对应着较高的故障误报率。因此,利用另外一组500个正常样本组成的测试数据集测试DPCA、DLV以及MI-DPCA方法对正常工况的误报率,详情列于表2中。从表中可以看出,MI-DPCA方法的两个统计量都能取得最低的故障误报率。相比于其他两种方法,本文所提出的MI-DPCA方法更可靠。通过上述对比分析,充分验证了基于MI-DPCA的过程监测方法的优越性和有效性。
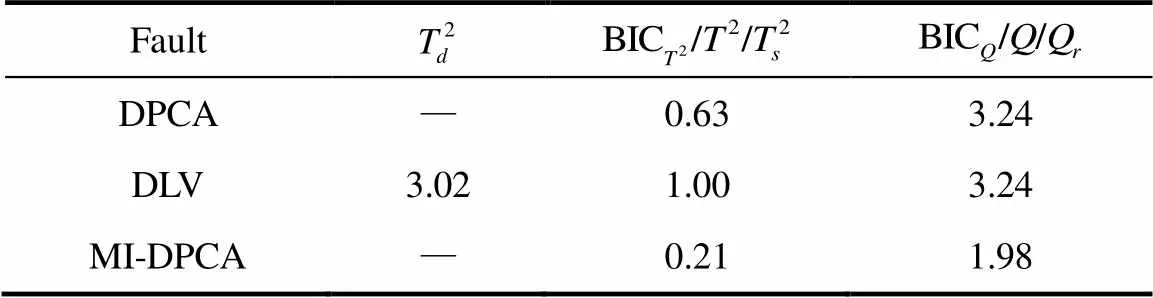
表2 TE过程故障误报率
4 结 论
本文提出了一种基于MI-DPCA的统计过程监测方法。考虑到不同测量变量会存在不同的自相关性且变量间的相互影响(即交叉相关性)会体现在不同的采样时刻上,该方法利用互信息为每个测量变量单独的找出与之相关的测量值。在此基础上得到的变量子块能较好地解决复杂动态过程在不同时滞上的相关性交错问题。该方法还利用了分散式建模的方式用多个统计监测模型并行实施故障检测,在针对大规模过程对象的监测问题上,理应取得较好的故障检测结果。在TE过程上的仿真研究也通过实例说明了MI-DPCA方法优越于DPCA与DLV方法。然而,MI-DPCA仍旧是一种线性建模方法,传统PCA监测模型的缺陷同样存在于MI-DPCA模型中。如何应对非线性、非高斯、多工况的复杂过程对象对下一步的工作提出了挑战。此外,本文的研究只限于故障检测,还未涉及后续的故障诊断,未来还需要开展相应的研究工作。
References
[1] GE Z, ONG Z, GAO F. Review of recent research on data-based process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52 (10): 3543-3562.
[2] YIN S, DING S X, XIE X,. A review on basic data-driven approaches for industrial process monitoring [J]. IEEE Transactions on Industrial Electronics, 2014, 61 (11): 6418-6428.
[3] QIN S J. Statistical process monitoring: basics and beyond [J]. Journal of Chemometrics, 2003, 17 (7/8): 480-502.
[4] 童楚东, 史旭华. 基于互信息的PCA方法及其在过程监测中的应用 [J]. 化工学报, 2015, 66 (10): 4101-4106. TONG C D, SHI X H. Mutual information based PCA algorithm with application in process monitoring [J]. CIESC Journal, 2015, 66 (10): 4101-4106.
[5] KU W, STORER R H, GEORGAKIS C. Disturbance detection and isolation by dynamic principal component analysis [J]. Chemometrics & Intelligent Laboratory Systems, 1995, 30 (1): 179-196.
[6] FAN J, WANG Y. Fault detection and diagnosis of nonlinear non-Gaussian dynamic processes using kernel dynamic independent component analysis [J]. Information Science, 2014, 259: 369-379.
[7] KERKHOF P V D, GINS G, VANLAER J,. Dynamic model-based fault diagnosis for (bio)chemical batch processes [J]. Computers & Chemical Engineering, 2012, 40: 12-21.
[8] LI G, QIN S J, ZHOU D. A new method of dynamic latent-variable modeling for process monitoring [J]. IEEE Transactions on Industrial Electronics, 2014, 61 (11): 6438-6445.
[9] ZHANG Y, ZHOU H, QIN S J,. Decentralized fault diagnosis of large-scale processes using multiblock kernel partial least squares [J]. IEEE Transactions on Industrial Informatics, 2010, 6 (1): 3-10.
[10] ZHANG Y, MA C. Decentralized fault diagnosis using multiblock kernel independent component analysis [J]. Chemical Engineering Research Design, 2012, 90 (5): 667-676.
[11] TONG C, SONG Y, YAN X. Distributed statistical process monitoring based on four-subspace construction and Bayesian inference [J]. Industrial & Engineering Chemistry Research, 2013, 52 (29): 9897-9907.
[12] GE Z, SONG Z. Distributed PCA model for plant-wide process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52 (5): 1947-1957.
[13] JIANG Q, WANG B, YAN X. Multiblock independent component analysis integrated with Hellinger distance and Bayesian inference for non-Gaussian plant-wide process monitoring [J]. Industrial & Engineering Chemistry Research, 2015, 54 (9): 2497-2508.
[14] LI W. Mutual information functionscorrelation functions [J]. Journal of Statistical Physics, 1990, 60 (5/6): 823-837.
[15] HAN M, REN W, LIU X. Joint mutual information-based input variable selection for multivariate time series modeling [J]. Engineering Applications of Artificial Intelligence, 2015, 37: 250-257.
[16] DOWNS J J, VOGEL E F. A plant-wide industrial process control problem [J]. Computers & Chemical Engineering, 1993, 17 (3): 245-255.
[17] VERRON S, TIPLICA T, KOBI A. Fault detection and identification with a new feature selection based on mutual information [J]. Journal of Process Control, 2008, 18 (5):479-490.
[18] JIANG Q, YAN X. Plant-wide process monitoring based on mutual information-multiblock principal component analysis [J]. ISA Transactions, 2014, 53 (5): 1516-1527.
[19] GE Z, SONG Z. Multimode process monitoring based on Bayesian method [J]. Journal of Chemometrics, 2009, 23 (12): 636-650.
[20] 赵忠盖, 刘飞. 因子分析及其在过程监控中的应用 [J]. 化工学报, 2007, 58 (4): 970-974. ZHAO Z G, LIU F. Factor analysis and its application to process monitoring [J]. Journal of Chemical Industry and Engineering (China), 2007, 58 (4): 970-974.
[21] TONG C, PALAZOGLU A, YAN X. Improved ICA for process monitoring based on ensemble learning and Bayesian inference [J]. Chemometrics & Intelligent Laboratory Systems, 2014, 135: 141-149.
[22] 韩敏, 张占奎. 基于改进核主成分分析的故障检测与诊断方法 [J]. 化工学报, 2015, 66 (6): 2139-2149. HAN M, ZHANG Z K. Fault detection and diagnosis method based on modified kernel principal component analysis [J]. CIESC Journal, 2015, 66 (6): 2139-2149.
Fault detection by decentralized dynamic PCA algorithm on mutual information
TONG Chudong, LAN Ting, SHI Xuhua
(Faculty of Electrical Engineering & Computer Science, Ningbo University, Ningbo 315211, Zhejiang, China)
For modern large-scale complex dynamic processes, different measured variables have their own serial correlations and interactions among these variables show on different time points. A mutual information based dynamic fault detection method was proposed by an advantageously decentralized modeling strategy. After made multiple time-delayed observations on each variable, the relevant measurements for the variable were separated from all observations by utilizing mutual information and corresponding variable sub-blocks were created. This approach of variable grouping allowed each variable sub-block to capture sufficient information about its own self- and inter-correlations such that the dynamic characteristics of process data could be well analyzed. The principal component analysis (PCA) algorithm was employed to construct statistical modeling on each variable sub-block and a decentralized dynamic fault detection model for large-scale dynamic process. The feasibility and effectiveness of the proposed method on dynamic process modeling were validated by a case study of a chemical process.
principal component analysis; process systems; mutual information; fault detection; statistical process monitoring
2016-02-29.
TONG Chudong, tongchudong@nbu.edu.cn
10.11949/j.issn.0438-1157.20160218
TP 277
A
0438—1157(2016)10—4317—07
国家自然科学基金项目(61503204);浙江省自然科学基金项目(Y16F030001);浙江省公益技术研究项目(2015C31017);浙江省信息与通信工程重中之重学科开放基金项目(XKXL1526)。
2016-02-29收到初稿,2016-07-14收到修改稿。
联系人及第一作者:童楚东(1988—),男,博士,副教授。
supported by the National Natural Science Foundation of China (61503204), the Natural Science Foundation of Zhejiang Province (Y16F030001), the Science & Technology Planning Project of Zhejiang (2015C31017) and the Key Discipline Fund of Information and Communication Engineering of Zhejiang (XKXL1526).

