基于空间频率域非局部总变差的压缩磁共振图像

张宝强 蔡述庭



基于空间频率域非局部总变差的压缩磁共振图像

张宝强 蔡述庭

（广东工业大学自动化学院）

非局部总变差本质上是一种局部去噪方法，该方法的不足是无法利用整幅图像的冗余性来进一步减少噪声方差。为获得一个更加真实有效的非局部解决方法，以傅里叶变换为依据，在非局部总变差的基础上提出一种新的变分模型，这种方法称为空间频率域非局部总变差。该算法归结为最小二乘数据拟合、空间频率域非局部总变差和小波系数正则化的最小化线性组合。在模型求解方面，利用快速组合算法可实现快速收敛，提高算法的求解速度。经仿真验证，该算法处理速度更快，图像复原效果更好，可用于压缩磁共振图像复原中。

磁共振图像；非局部总变差；傅里叶变换；快速组合分裂算法

0　引言

目前，磁共振成像由于对软组织有极好的分辨率和对人体没有电离辐射损伤等优点，广泛应用于医疗诊断。然而从最近的压缩感知理论[1]发展可知，采用高度欠采样空间方法不仅能够精确地修复磁共振（magnetic resonance，MR）图像，并且可大幅度地缩短扫描时间[2]。非局部总变差（nonlocal total variation，NLTV）本质上是一种局部去噪方法，它能够在不破坏原始图像显著特征的情况下有效去除噪声，从而保留图像的更多细节和结构特征。本文在NLTV[3-4]模型的基础上提出了一种空间频率域非局部总变差（spatial-frequency nonlocal total variation ，SFNLTV）模型[5]。SFNLTV模型在视觉效果和信噪比方面比NLTV模型好，且SFNLTV模型选取的参数对整幅图像产生的影响不大。

1　非局部总变差模型

非局部总变差压缩磁共振图像的复原表达式为

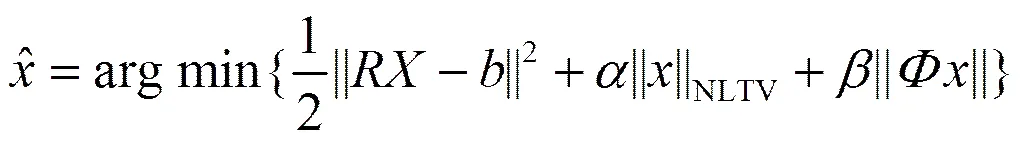
其中，正则化参数和为2个正数；为局部傅里叶变换；为原始磁共振图像；为空间欠采样数据的量度；为小波变换[6-7]。

非局部（nonlocal，NL）算子的主要思想是将梯度和散度2个传统的局部定义，通过图论的相关思想扩展到非局部，使用非局部平均（nonlocal means ，NLM）[8]方法计算像素间的相似度以得到各像素相互间的权重，从而构造非局部梯度算子和非局部散度算子。令，，，NL算子定义为

(2)

非局部散度算子定义为

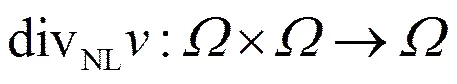
(3)

(,)为权重函数，非负且对称的非局部变量，用来表示,之间的差异。如果2个像素之间的结构越相似，则权重系数(,)越大，反之亦然。(,)的表达式为

其中，为滤波参数；为标准差为的高斯核，计算方法

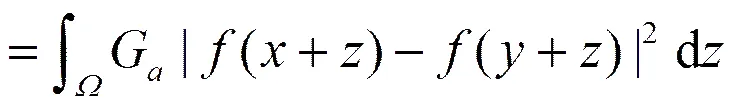
因此，NLTV半范数可表示为

(6)

2　改进的图像去噪算法

2.1空间频率域非局部总变差模型

为了能在MR图像中获得更好的复原结果，本文在NLTV模型的基础上引入傅里叶变换[9]，即空间频率域非局部总变差模型。空间频率域非局部总变差压缩磁共振图像的复原表达式为

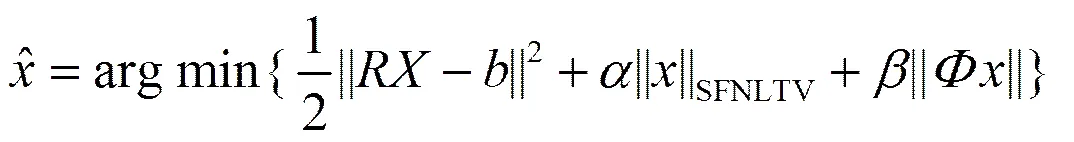
空间频率域总变差模型的正则化表达式为

(8)

定义的傅里叶变换为，可得

(9)

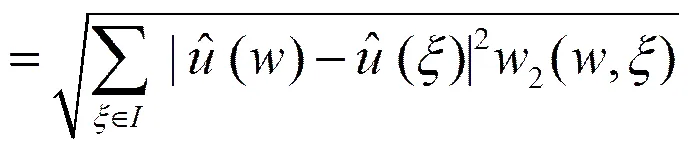
(11)

(12)

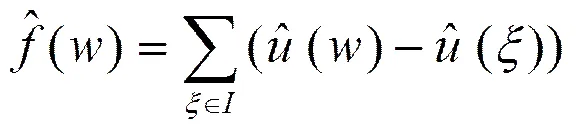
(13)

首先，令

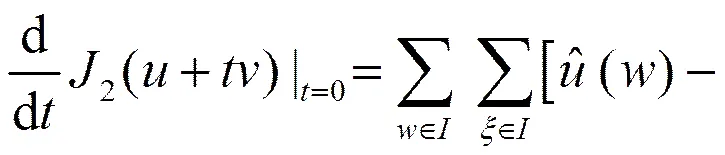
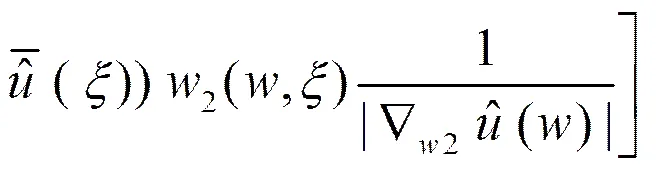
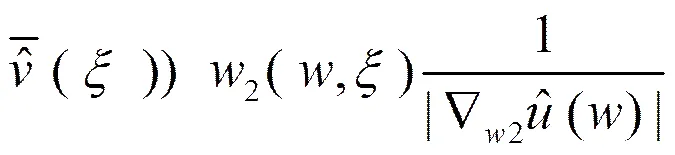
(15)

结合(14)和(15)，可得

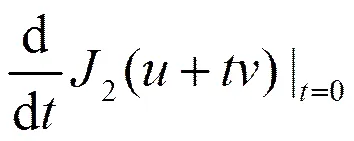
2.2SFNLTV-FCSA算法

快速组合分裂算法[11]（fast combination splitting algorithm，FCSA）是一种快速迭代收缩阈值算法，其最大特点是能够实现算法的快速收敛。由于这个特点，使得它与SFNLTV模型组合成SFNLTV- FCSA算法。

SFNLTV-FCSA算法的具体流程：

2)循环开始，迭代次数=1,2,...,；

①分别求邻近映射1、2的值，

；

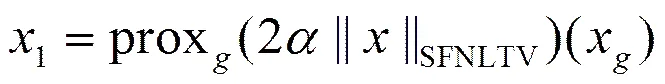
=+1；

3　实验分析

3.1可视化比较

设定正则化参数和的值分别为0.001和0.035，同时给定输入参数和，是最终结果。用峰值信噪比（PSNR）衡量复原图像的质量

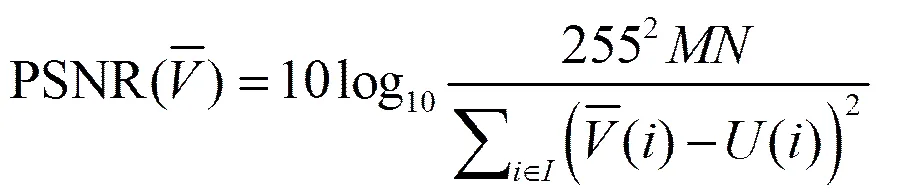
选取块大小均为256像素×256像素的心脏磁共振图像、大脑磁共振图像、胸部磁共振图像、动脉磁共振图像，在采样比均为20%的情况下进行实验，同时把本文提出的SFNLTV-FCSA算法与共轭梯度法CG[13]、TVCMRI[14]、RecPF[15]和NLTV-FCSA等算法进行对比。为了能够很好地进行比较，除了CG的计算复杂度很高，只迭代运行10次外，其他方法迭代运行50次，图1~图4表示使用不同的处理方法获得的不同视觉效果。

Original     CG      TVCMRI

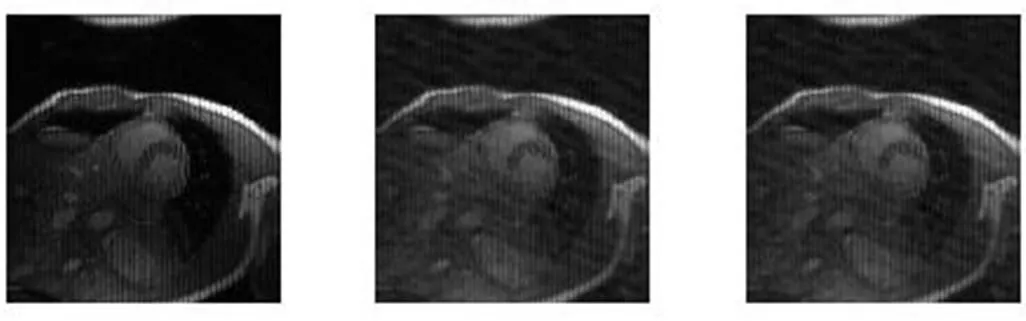
RecPF     NLTV-FCSA      SFNLTV-FCSA

Original      CG      TVCMRI

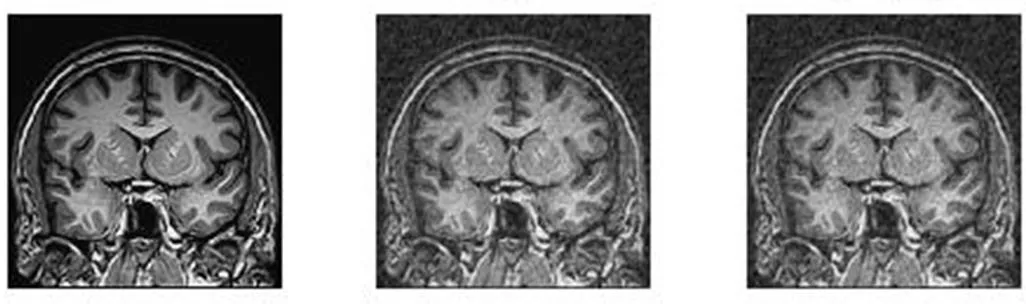
RecPF      NLTV-FCSA      SFNLTV-FCSA

Original      CG      TVCMRI

Original      CG      TVCMRI

3.2CPU运行时间和SNR

本文提出的SFNLTV-FCSA算法与共轭梯度法CG、TVCMRI、RecPF和NLTV-FCSA等算法在CPU运行时间和信噪比方面的性能比较如图5所示。表1、表2给出了在每个实验重复进行100次的情况下，使用不同方法得到的不同CPU运行时间和SNR。由图5可知，采用SFNLTV-FCSA算法花费的时间更少，但却获得了更好的视觉效果，在CPU运行时间和SNR方面比NLTV-FCSA要好；而CG由于迭代计算复杂度较高，获得的复原效果也最差，RecPF仅比TVCMRI略好一点，比NLTV-FCSA要差一些。

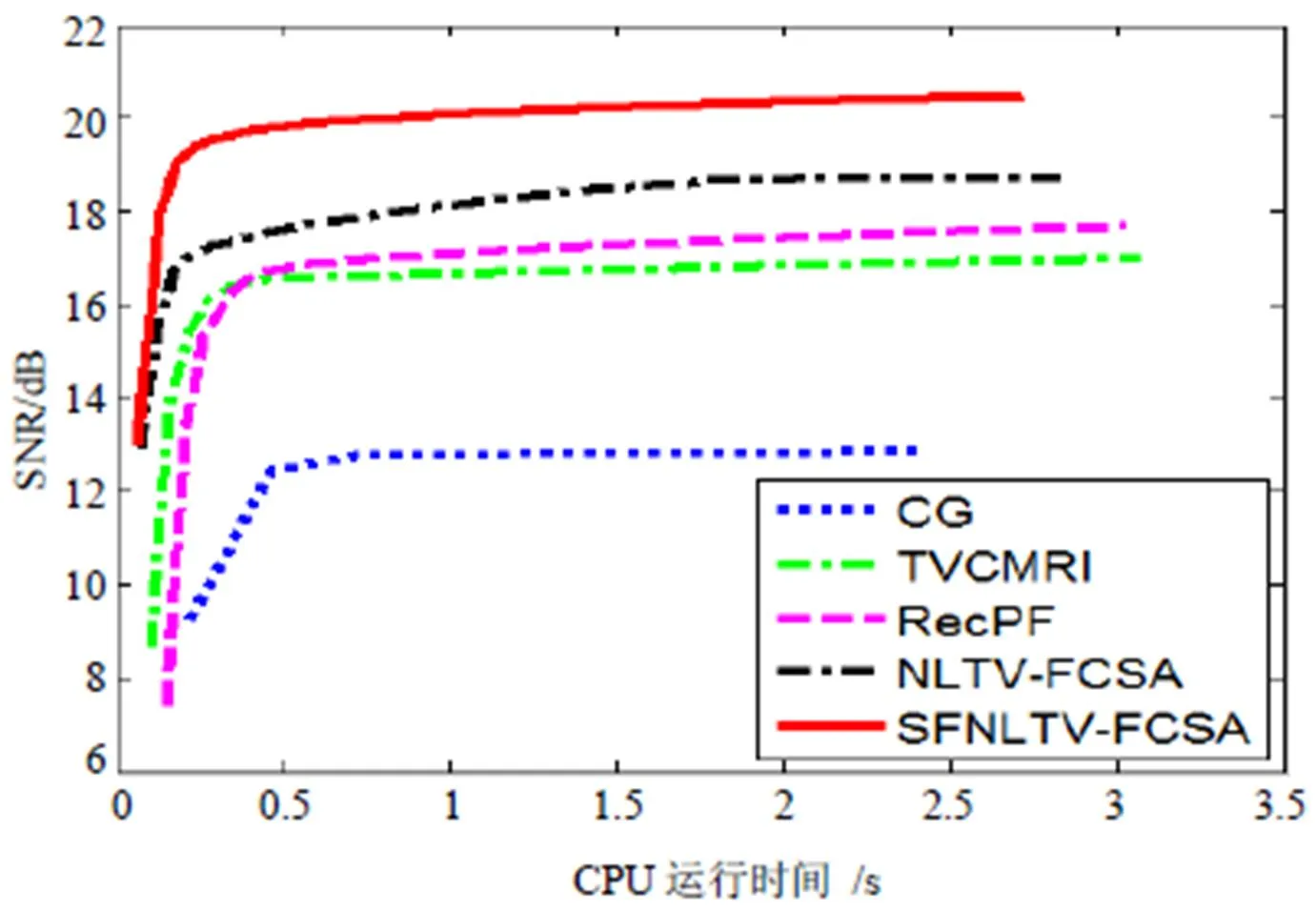
图5 (a)　心脏图像

(b)大脑图像

(c)胸部图像

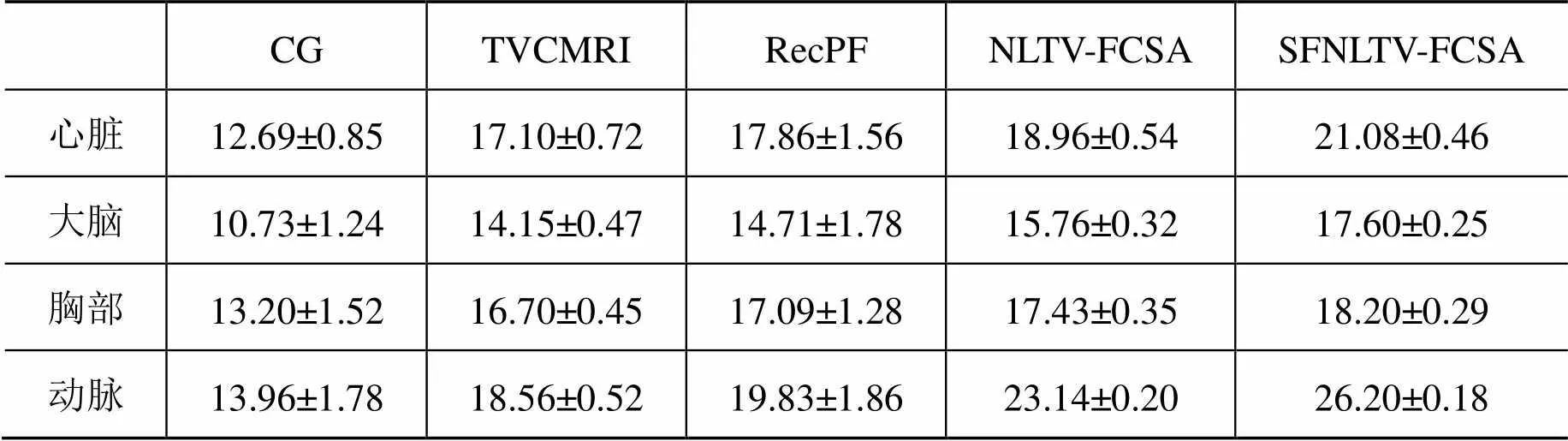
表1　重复100次实验信噪比的比较 （单位：dB）

表2　重复100次实验CPU运行时间比较 （单位：s）

4　结语

本文提出一种高效的压缩MR图像复原算法。首先，SFNLTV-FCSA能有效解决SFNLTV项和L1范数项复合正则化问题，也更容易应用在其他医学图像领域。其次，快速组合分裂算法在每次迭代的过程中计算复杂度只有(plog())，其中表示复原图像中的像素值，明显提高了计算效率。然后，它具有很强的收敛性，使压缩MR图像复原方法比以前的方法执行效率更高。最后，通过实验证明，SFNLTV-FCSA算法在精确度和复杂度方面比一些经典的算法效果更好。此外，由于正则化参数和都是手动固定的，在未来工作中将尽力根据需求自我调整正则化参数，以求图像达到最好的复原效果。

[1] 刘海英.基于压缩感知理论的高光谱图像重建和超分辨成像技术研究[D].西安:西安电子科技大学,2014.

[2] Lustig M, Donoho D, Pauly J M. Sparse MRI: The application of compressed sensing for rapid MR imaging[J]. Magnetic Resonance in Medicine, 2007, 58(6):1182-1195.

[3] 徐焕宇,孙权森,夏德深.基于非局部总变差的消除不规则采样遥感图像复原方法[J].测绘学报,2012,41(2):232-238.

[4] Lou Y, Zhang X, Osher S, et al. Image recovery via nonlocal operators[J]. Journal of Scientific Computing, 2010,42(2): 185-197.

[5] Hu H, Froment J. Nonlocal total variation for image denoising[J]. Photonics & Optoelectronics, 2012:1-4.

[6] 张军,成礼智,杨海滨,等.基于纹理的自适应提升小波变换图像压缩[J].计算机学报,2010,33(1):184-192.

[7] 宋佳伟,徐煜明,肖贤建.基于小波变换和迭代反向投影的超分辨率算法[J].计算机技术与发展,2015,25(2):74-77.

[8] 杨帆.图像非局部均值滤波去噪和修复算法的改进研究[D].南昌:南昌航空大学,2015.

[9] 司祯祯.傅里叶变换与小波变换在信号去噪中的应用[J].电子设计工程,2011,19(4):155-157.

[10] 茆晓军,王军锋,刘兴钊.基于梯度下降法的ISAR最小熵相位校正算法[J].现代雷达,2008,30(1):40-43.

[11] Huang J, Zhang S, Metaxas D. Efficient MR image reconstruction for compressed MR imaging[C]// International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer-Verlag, 2010: 135-142.

[12] 余平洋.共轭梯度算法的收敛性研究[D].郑州:郑州大学,2013.

[13] Ma S, Yin W, Zhang Y, et al. An efficient algorithm for compressed MR imaging using total variation and wavelets[C]// 2008:1-8.

[14] Yang J, Zhang Y, Yin W. A fast alternating direction method for TVL1-L2 signal reconstruction from partial Fourier data[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):288-297.

[15] Huang J, Yang F. Compressed magnetic resonance imaging based on wavelet sparsity and nonlocal total variation[J]. Proceedings, 2012, 5(1):968-971.

Compressed Magnetic Resonance Image Based on Nonlocal Total Variation Spatial-Frequency Domain

Zhang Baoqiang Cai Shuting

(Institute of Automation, Guangdong University of Technology)

NLTV is essentially a local denoising scheme and the shortcomings of this approach is unable to use redundancies in the whole image to further decrease the noise variance. In order to obtain a more realistic and effective nonlocal solution, this paper propose a new variational model by adding to NLTV a term based on the Fourier transform, we call this new scheme spatial-frequency domain nonlocal total variation (SFNLTV). This algorithm formulated as the minimization of a linear combination of three terms corresponding to a least square data fitting, spatial-frequency domain nonlocal total variation (NLTV) and wavelet sparsity regularization. In term of solving the model, using fast composite splitting algorithm(FCSA) can achieve fast convergence, improve the speed of solving the algorithm. The simulation show that the processing speed of the algorithm is fast, and obtained better reconstruction result, can be applied to compressed magnetic resonance(MR) image.

Magnetic Resonance Image; Nonlocal Total Variation; Fourier Transform; Fast Composite Splitting Algorithm

张宝强，男，1990年生，硕士研究生，主要研究方向：图像处理。E-mail: 739073853@qq.com

蔡述庭，男，1979年生，副教授，研究生导师，主要研究方向：多媒体信号处理。