基于A*算法的无人机攻击编队航迹规划

曹　栋，王　瑞，曹　越

(1.海军航空兵学院 a.司令部;b.飞行理论系，辽宁 葫芦岛 125001； 2.中航工业无线电电子研究所 军机系统部，上海 200233)



基于A*算法的无人机攻击编队航迹规划

曹栋1a，王瑞1b，曹越2

(1.海军航空兵学院 a.司令部;b.飞行理论系，辽宁 葫芦岛 125001； 2.中航工业无线电电子研究所 军机系统部，上海 200233)

提出了一种改进的A*算法，对无人机编队飞行的航迹进行规划。根据无人机在编队飞行时对油耗、航迹长短、编队队形及目标威胁等约束条件来设计合适的评估函数。采取对规划点前后段航迹评估进行加权的方法对A*算法进行改进，从而在优化航迹与减少计算时间之间找到平衡点。改进在Open表中插入与删除节点的方式，提高计算效率。仿真结果表明，设计的A*算法可以快速、有效地为无人机编队飞行规划出合理的航迹。

无人机；航迹规划；编队飞行；A*算法

无人机(Unmanned Aerial Vehicle，UAV)能够自主进行航迹的选择与设定，是实现全自主、全任务飞行能力的必要前提条件，所以UAV航迹规划成为当前无人机研究的一个热点[1-6]。与单架UAV相比，多UAV协同作战具有任务能力强、灵活性高、容错性好等优点，因此UAV编队执行作战任务将成为未来战争的一种重要模式[7-8],UAV编队飞行的航迹生成是多UAV协同作战的关键技术[9]。

UAV编队的航迹规划包括2个方面[10]：一方面，编队整体的航迹规划包括规避已知和未知的危险、临时任务的调整等问题；另一方面，是编队内部各UAV间的约束，包括各机通信、队形控制、各机航迹最优化等问题。对于第一个问题，可以借助单架UAV的航迹设计与优化方法，采用A*算法、Voronoi图法、概率地图法、遗传算法等[1-6,11]，在设计编队航迹的同时，引入编队飞机之间的约束条件，从而实现对编队航迹的规划[12]。目前，通过以上方法虽然能够实现对多UAV编队的航迹规划和任务分配，但是普遍存在实时性不强的缺点。其原因是由于采用的航迹规划算法效率不高，最优化时选取的评估函数过于复杂所造成的。

本文基于改进的A*算法进行设计，选取较为简单的评估函数，从而提高了UAV编队航迹规划的时效性。

1　评估函数的选定

编队航迹的评估函数既需要考虑整体航迹的优化也需要考虑编队内部成员之间的优化限制问题。对于前者，可以将之视为有向图的最优路线问题[6]。通过使公式(1)所示的评估函数最小来得到最优解[13]。

(1)

式(1)中，L(μ)为编队规划航迹μ的长度，lij为航迹μ上相邻两点的弧线长度。为使评估最小，选取的性能指标可以用以下的广义评估函数W表示[14]。

(2)

式(2)中，ωi为航路的威胁评估，ωf为航路的油耗评估，k为油耗与威胁之间的权重系数。

但是对于编队内部多UAV队形的控制问题，需要对以上的评估函数进行改造。在进行编队飞行时，UAV的距离既要保证在安全距离之外，也要保证在可通信的范围之内，同时还需要避免被敌方雷达探测，如图1所示。

图1中，RC表示UAV的探测通信距离，RS表示UAV的最小安全间距，RT表示目标的探测距离。在飞行时，UAV的间距应该保持在RC和RS之间，如U1和U2所示，即需要遵循以下的限制条件：

(3)

式(3)中，(xm，ym)是编队中第m个UAV在时刻t处的平面坐标。假定采用三机编队并考虑到队形的紧凑，在某段航迹lij处可以选取以下的评估函数。

图1　UAV编队

(4)

W′=∑[k′Wij+(1-k′)W]

(5)

式(5)中，k′为权重系数，W为离散形式，如式(6)所示。

W=∑[kωi(i,j)+(1-k)ωf(i,j)]

(6)

2　A*算法及其改进

A*算法是一种基于启发函数的搜索算法。通过定义并满足相容性条件(评估函数)，进而在已知地图中生成一条最优路径[15]，如式(7)所示。

f(n)=g′(n)+h′(n)

(7)

式(7)中，g′(n)表示当前节点(第n个节点)与起点之间航迹的估计评估，h′(n)表示当前节点与终点之间航迹的估计评估。A*算法加入了与航迹规划有关的启发函数，对航迹点的搜索方向更加趋向于最终点，从而减小了搜索深度和节点数，提高了效率。但为满足A*算法的可接纳性[16]，任一时刻的h′(n)不能超过从网格上的方格移动到终点的实际移动耗费h(n)，这样A*算法的效率提高，航迹却优化不够。因此，需要考虑对A*算法进行改进。

2.1A*算法的改进

通过调整g′(n)和h′(n)在启发函数f(n)中的权重，来减少估价函数中前后段航迹所占的比例，以在效率和最优化之间找到一个平衡点，即调整启发函数，如式(8)所示。

f(n)=q·g′(n)+(1-q)h′(n)

(8)

式(8)中，q为权重比，考虑到g′(n)和h′(n)的权重比不小于1∶1，其取值范围为0.5～1，当q取1时，相当于Dijkstra算法。当q逐步减小即增大h′(n)的权重时，效率提高；反之，效率降低，航迹最优。通过调整q，可使航迹最优的同时，提高A*算法的时效性和可接纳性。

根据式(5)和式(8)可将评估函数列写为A*算法的形式。

(9)

(10)

h′(n)为节点n以后的飞行路线的估计值(假定UAV采用大圆线飞行)。

2.2A*算法的步骤

编写A*算法程序时,需要构造Open表和Closed表分别用于存储待扩展的节点和已扩展的节点[17]。由于传统Open表的节点插入速度和删除速度相互制约，不能同时提升，难以整体提高算法效率，所以根据文献[13]的方法，采用改进的双向链表的Open表标记插入排序方法，有效地提高了算法的计算速度。

A*算法改进之后的流程如图2所示。

3　编队仿真

根据设计的A*航迹规划算法，针对三架UAV编队飞行时的航迹进行仿真，仿真环境为Matlab7.6。仿真过程中，需要对每架UAV的航迹进行计算，最后结果统一在图示中给出。选择的编队有两种形式，分别为“△”形和“─”形，飞行环境为二维平面。

规划的航迹起始点设定为(100,100)，目标点为(110,120)和(120,110)，目标点周围5格范围内为危险区域，到达目标后需经(120,100)返回起始点。UAV的安全防撞区域设定为2，探测距离设定为10。进行仿真计算时，q的取值分别设定为0.5、0.7和1，所得到的仿真结果如图3和图4所示。

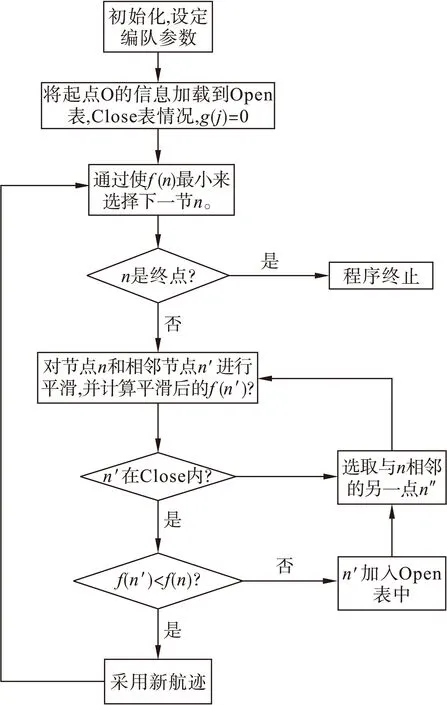
图2　改进A*算法流程图

图3　“△”编队总体航迹

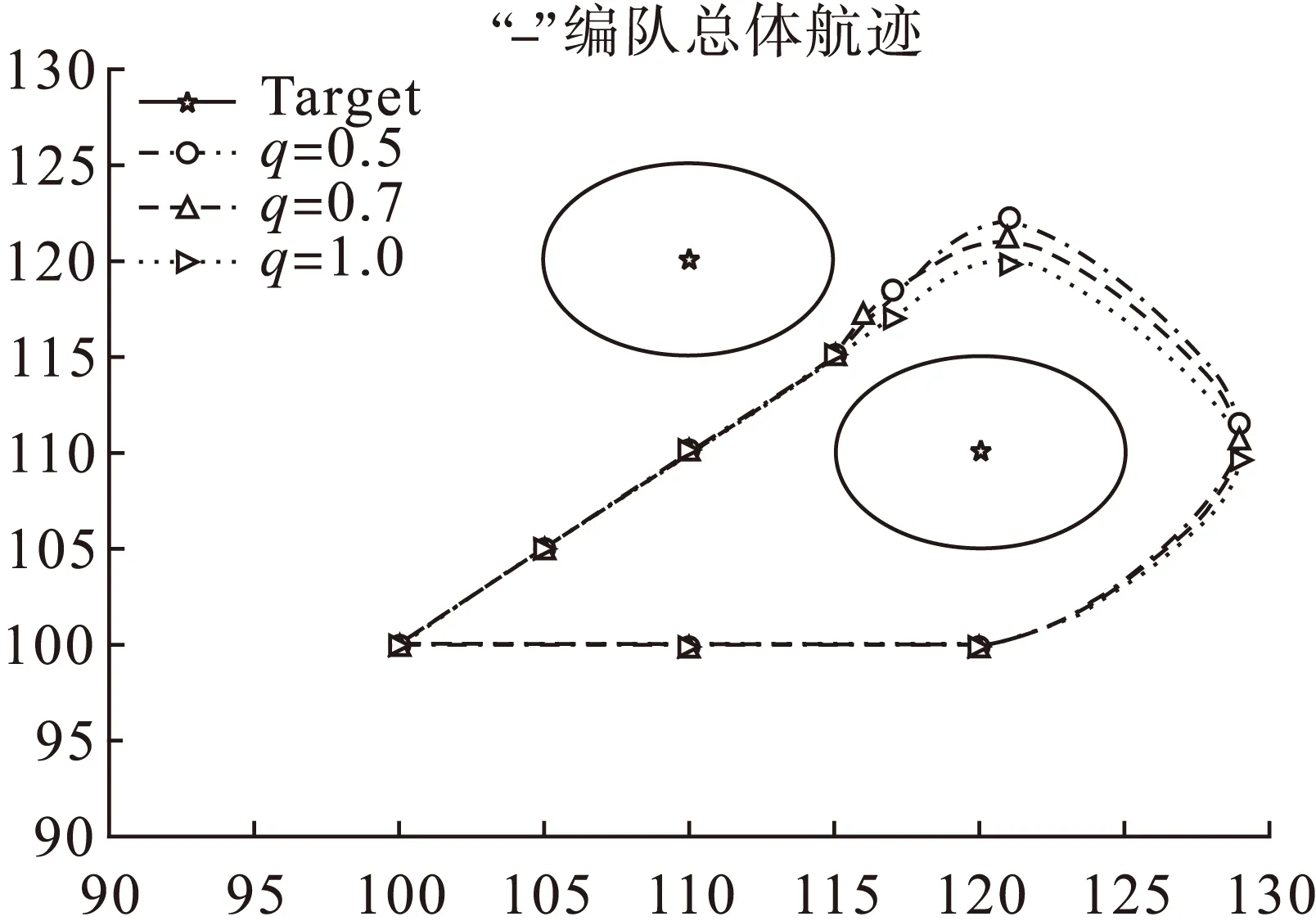
图4　“─”编队总体航迹

图5为在q=0.7时“△”队形和“─”队形中所有UAV的规划航迹。从图5中可以看出，按照本文所提出的算法规划编队航迹，虽然在局部地方队形的航迹有所波动，但是整体与预期的设定要求相符，这也说明了算法的有效性。

图5　编队内部UAV航迹

对比以上的仿真图形，可以看出，采用“△”编队时，由于两目标间距过小，需要绕过两个目标点。而采用“─”队形时，可从两目标中间穿过，所以前者规划的航迹比后者的长。同时，可以看出采用不同的q值对航迹的影响。随着h′(n)权重的增加，航迹优化效果变差，当q取中间的某一值时(待验证)，可以在优化效果与计算时间之间取得平衡，不同q值所对应的计算时间如表1所示。

表1　计算耗费

从表1可以看出，随着q取值增大，所用计算时间逐渐增大，耗费资源增多。同时，采用双向Open链表所用的计算时间比单向Open链表所用时间短，说明根据文献[13]提出的Open表计算方法具有一定优势。

综合仿真数据可以看出，在权值q取0.5时相当于原A*算法，从图3-5可看出据此规划出的航迹较优，但据表1可见其计算时间较长。而q取1时，相当于Dijkstra算法，航迹较差但计算效率较高。因此，综合两种算法的优势，对原A*算法进行改进，使q取值为0.7，就可以得到较优的航迹和较高的计算效率，双向Open链表的计算时间分别为6.2s和6.05s。但q的最优取值还需对航迹优劣的评估方法进行研究之后才能综合确定。

4　结论

相对于单架UAV执行任务，多架UAV协同执行任务具有更多的优势。针对UAV编队飞行的航迹规划问题，本文设计了相应的评估函数，通过调整启发函数前后段所占权重以及采用双向Open链表的方法对A*算法进行改进。最后的仿真结果表明，通过调整启发函数前后段的权重可以在航迹优化效果和计算时间之间得到平衡，在保证航迹可行的情况下提高计算效率。同时采用双向链表的方法可以节省计算时间，提升效率。但是在飞行中，如果UAV编队队形改变，航迹也会相应改变，而相关的航迹规划问题需要进一步的研究。

[1]高晖,陈欣,夏云程.无人机航路规划研究[J].南京航空航天大学学报,2001,33(2):135 -138.

[2]周炜，魏瑞轩，董志兴.基于层次分解策略无人机编队避障方法.系统工程与电子技术[J]，2009，31(5)：1152-1157.

[3]安玉娇，江辉军，郑根营，等.无人机低空突防航迹规划算法研究[J].测控技术，2011，30(12)：86-90.

[4]王绪芝，姚敏，赵敏，等.基于蚁群算法的无人机航迹规划及其动态仿真[J].指挥控制与仿真，2012，34(1):29-32.

[5]任波，周焘，于雷.基于改进A*算法的飞行器三维航迹规划算法.系统工程与电子技术[J]，2008，30(2)：324-326.

[6]ALEXY，SANJIVS，ANTHONYS.Anefficientonlinepathplannerforoutdoormobilerobots[J].RoboticsandAutonomousSystems,2000,32:129-143.

[7]王国强，罗贺，胡笑旋，等.无人机编队管理的研究综述[J].电光与控制，2013，20(8)：48-53.

[8]刘小雄，章卫国，王振华.无人机自适应编队飞行控制设计与仿真[J].系统仿真学报，2009，21(5):1420-1422.

[9]胡中华.基于智能优化算法的无人机航迹规划若干关键技术研究[D].南京:南京航空航天大学，2011.

[10]朱艳萍.多无人机协同攻击策略研究[D].南京:南京航空航天大学，2012.

[11]何平川，戴树岭.一种改进的UAV三维航迹实时规划算法[J].北京航空航天大学学报，2010，36(10)：1248-1251.

[12]王庆江，高晓光，符小卫.无威胁情况下任意两点间的无人机路径规划[J].系统工程与电子技术，2009，31(9)：2157-2162.

[13]FENGLILIAN,RICHARDMURRAY.Real-timetrajectorygenerationforcooperativepathplanningofmulti-vehiclesystems[C].2002ConferenceonDecisionandControl.California,2002:1-4.

[14]张大巧，鲜勇，许立军，等.基于改进A*的三维航迹快速规划方法[J].弹箭与制导学报,2010，30(5)：59-62.

[15]史辉，曹闻，朱述龙，等.A*算法的改进及其在路径规划中的应用[J].测绘与空间地理信，2009，32(6)：208-211.

[16]赵真明，孟正大.基于加权A*算法的服务型机器人路径规划[J].华中科技大学学报(自然科学版)，2008，36(SupⅠ)：196-198.

[17]HENNEBRYMICHAE,JIANKUOD,NYGARDKENDALL.Dynamicnetworkrefinementinautomatedaircraftrouteplanning[C].IEEEEIT2007Proceedings.Chicago:IEEE,2007:373-377.

[18]冯乃勤，王岁花，郑延斌，等.OPEN表和CLOSED表的合一[J].计算机工程与应用，2003(16):100-102.

(责任编辑：吴萍英文审校：赵亮)

Trajectory planning for flight formation of Unmanned Aerial Vehicle based on A*algorithm

CAO Dong1,WANG Rui1,CAO Yue2

(1.a.Headquarters;b.Department of Flight Thoery,Naval Air Institute,Huludao 125001, China;2.System Department of attle Aircraft,China Aeronautical Radio Electronics Research Institute Shanghai 200233,China)

An improved A*algorithm was proposed to plan the trajectory for Unmanned Aerial Vehicle formation in the paper.First the cost function was designed on the basis of fuel consumption,length of trajectory,formation shape and dangers of targets while unmanned aerial vehicles were flying in formation.Then the A*algorithm was used by adding-weight to the evaluations of trajectory before or after the knot being expanded.As a result,the balance between trajectory optimization and computing time was found.Meanwhile the computing efficient was also improved by changing the method of deleting and adding knot in the open list.The simulation results show that the A*algorithm can plan optimized trajectories for unmanned aerial vehicles flying in formation quickly and efficiently.

unmanned aerial vehicle;trajectory planning;flight formation;A*algorithm

2016-02-16

曹栋(1962-)，男，江苏南通人，教授，主要研究方向：航空电气与控制，E-mail:hfcd39325@sina.com。

2095-1248(2016)04-0061-05

V249.4

A

10.3969/j.issn.2095-1248.2016.04.011