基于VOF方法的海底管道溢油扩散数值模拟研究
李志刚,蒋梅荣,余建星
(1. 海洋石油工程股份有限公司,天津 300451; 2. 天津大学 水利工程仿真与安全国家重点实验室,天津 300072; 3. 中海油研究总院,北京 100028)
基于VOF方法的海底管道溢油扩散数值模拟研究
李志刚1, 2, 3,蒋梅荣1, 2, 3,余建星2
(1. 海洋石油工程股份有限公司,天津 300451; 2. 天津大学 水利工程仿真与安全国家重点实验室,天津 300072; 3. 中海油研究总院,北京 100028)
在海底输油管道运行过程中,管道渗漏、穿孔及破碎都会导致原油泄漏。对溢油运动的轨迹及其扩散范围作出预报可为溢油事故的处理提供及时、准确的信息,指导应急处理的正确实施。基于工程实际需求,采用有限体积法,结合k-ε紊流模型,建立了海流作用下海底输油管道溢油扩散数值模型。采用VOF方法(volume of fluid method)追踪多相流界面。首先,将数值模拟结果与Fan的实验值及Zheng和Yapa的数值结果进行了对比,验证数值模型的可靠性;其次,研究了不同原油溢出速度与环境水深对不同时刻溢油轨迹、到达海面时间、横向漂移距离与海面扩散范围的影响。研究表明:随原油溢出速度增大,溢油到达海面时间逐渐减小,溢油横向漂移距离与海面扩散范围则逐渐增大;随环境水深增大,溢油到达海面时间逐渐增大,且其变化接近线性分布。
海底管道;溢油;湍流;有限体积法;VOF方法
Abstract: During the operation process of submarine oil pipeline, oil spill may occur due to leakage, perforation and fragmentation. The correct forecast of the spilling trajectory and the diffusion range can provide timely information for the handling of the oil spill accidents. Based on the Finite Volume Method, the k-ε turbulence model is introduced to establish an oil spill numerical model for the submarine pipeline under the action of current. The VOF method (Volume Of Fluid method) is adopted to track the interface of multiphase flow phase. Firstly, the model simulation results are compared with the available experimental values (Fan, 1967) and the numerical results (Zheng and Yapa, 1998), thus proving the reliability of the present model. Furthermore, the influences of the crude oil spilling velocity and the environmental water depth on the oil trajectory at different times, the arriving time at the sea surface, the lateral drifting distance and the surface diffusion range are studied. The results show that with the increase of crude oil spilling velocity, the arriving time at the sea surface decreases, but the lateral drifting distance and the surface diffusion range are increased gradually; with the increase of the water depth, the arriving time at the sea surface increases gradually and its change is close to a linear distribution.
Keywords: submarine pipeline; oil spill; turbulence; finite volume method; VOF method
随着海上油气田的开发和工业技术的发展,海底管道在原油生产运输过程中起到了不可替代的重要作用。在海底管道运行的全过程中,管道渗漏、穿孔及破碎都会导致原油泄漏。海上石油泄漏在经济发展与海洋环境方面造成了巨大的损失与破坏。例如,从1995年到2002年七年间,国内仅350万元损失以上事故就有9项,其中,2001年东海平湖油田由于油管冲刷断裂,仅修复费用就多达2 000多万,永久修复历时一年多[1]。
近30年来,人们对于溢油对环境造成的破坏性影响的意识已逐渐增强,发展了50多种模型来预测溢油的行为和归宿[2-3]。对溢油运动的轨迹及其扩散范围作出预报可为溢油事故的处理提供及时、准确的信息,可以帮助应急决策者确保优先保护次序,正确调动抗溢油设施等,以确保应急计划得以有效、正确的实施。然而,目前国内外有关溢油的研究,基本上都是针对海面溢油过程中溢油的行为和归宿的预测,而对水下溢油在海水中运移扩散过程的研究则相对较少。
海底输油管道溢油一般分为两个阶段:1)原油从漏点溢出后在海水中的运移扩散过程;2)溢油到达海面之后在海上漂移的过程。如果我们在发现海面上的溢油之后配合当时的海洋及气象条件,能够反推出漏油的位置,就可以及时对漏点采取应急补救措施进行封堵;或者在溢油到达海面之前将其出现的位置预测出来,就可以在溢油发生扩散和漂移之初对溢油进行处理,这样既可以减小工作量,又可以减少溢油对海上环境的污染。
关于海底管道溢油预报模型的研究,始于20世纪70年代。Hirst[4]对二维和三维浮射流溢油进行了数值模型,并与海流作用下垂直浮射流轨迹实验值进行了对比。McDougall[5]、Fannelop等[6]、Milgram[7]、Fannelop等[8]建立了油井溢油模型,这些模型考虑了气体的膨胀,但仅局限于垂直溢油情况,并且没有考虑水流的作用。Bemporad[9]对分层流环境中圆孔浮射流轨迹进行了模拟。Yapa等[2]和Zheng等[10]基于Lagrangian积分法,建立了一个比较完善的溢油模型,该模型考虑了溢油的扩散和溶解过程,但没有考虑乳化过程。Johansen[11]和Zheng等[12]建立了适用于深水溢油的DeepBlow模型和CDOG模型。
我国在这方面的研究起步较晚。王晶[13]以Goncharov模型为基础进行了数值模拟,并研究了水下单一孔口的溢油/气,比较了各种因素对形成油滴/气泡和其上浮速度的影响。高清军[14]采用Fluent软件研究了不同海况、操作压力对水下小孔溢油的影响,但只是讨论了单一因素的作用,且未能给出溢油运动的轨迹。汪守东[3]采用Yapa和Zheng的溢油模型并基于POM和FVCOM水动力学模型,对海底管道溢油扩散及海面漂移进行了模拟。基于Fluent软件,Li等[15]与Zhu等[16]分别研究了不同操作压力、流速和波长变化下的溢油轨迹与不同原油密度、泄漏率和流速对溢油过程的影响。陈海波等[17]基于Lagrange积分法和粒子追踪法对水下溢油轨迹进行了模拟。
基于以上研究基础及工程实际需要,拟开展在不同原油物性条件、泄漏条件、海洋环境条件下,海底输油管道泄漏及溢油扩散仿真模拟分析的研究工作,研究溢油在水中的运移扩散过程及后果,考虑海洋环境及泄漏孔径等的影响,建立合理的溢油理论分析模型,同时开展溢油数值模拟研究,选取典型溢油场景建模计算,分析溢油扩散情形、影响范围及其影响后果,指导溢油事故的应急处理。
1 数值模拟方法
海底输油管道溢油扩散二维数值模型如图1所示。计算海域长为L(x方向),水深为h(y方向)。原油从输油管道破损溢油孔径中竖直向上溢出,以初始速度uoil流入密度为ρwater的均匀海水环境中,其初始速度与海床面成90°夹角。溢油孔径宽度为D,原油密度为ρoil、运动黏滞系数为υoil。上游有恒定来流,与海床面平行,其流速为uwater。
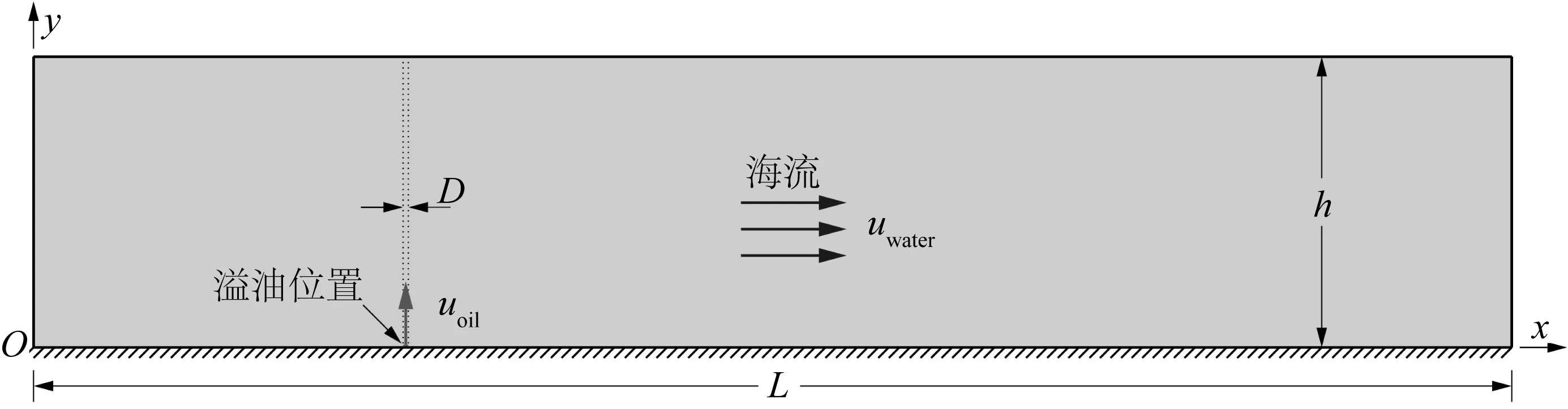
图1 海流情况下溢油示意Fig. 1 Sketch of oil spill under sea current
1.1 基本方程
控制方程采用连续方程与二维瞬态不可压缩雷诺时均Navier-Stokes方程:
连续方程
动量方程

k-ε模型非常适合用于包含有射流和混合流的自由流动模拟,因此采用k-ε模型来封闭雷诺时均N-S方程组。
k方程:
ε方程:
其中,μ和μt分别为流体的运动黏性系数和湍动黏性系数,k和ε为湍动能及其耗散率,且有:


1.2 VOF方法
采用流体体积法(VOF方法)来追踪多相流自由界面。该方法基本思想是通过构造流体体积分数函数F来追踪每个控制体内的流体流量,并根据其函数值和导数值构造自由面形状[18]。流体体积分数Fq定义为单元内第q相流体所占体积与该单元总体积之比。若Fq= 1,表示单元内全部为第q相流体;若Fq= 0,则表示单元内没有第q相流体;若0 在VOF方法中,物性参数φ由控制体积内各相流体物性参数及各相体积分数函数决定,由下式计算: 参照图1所示的海管溢油模型,计算区域由自由表面、左侧进口边界、右侧出口边界、壁面边界及溢油喷口边界组成。 5) 壁面边界:uwall=vwall=wwall=0 k-ε模型是针对充分发展的湍流模型,适用于高Re数区。而近壁区内的流动,Re较低。湍流发展不充分,不能采用k-ε模型计算,因此采用标准壁面函数法处理。 控制方程采用交错网格的有限体积法求解。控制方程离散格式采用QUICK格式,求解压力和速度耦合采用PISO算法。该算法由于使用了预测-修正-再修正二步,可以使(u,v,P)更好地同时满足动量方程和连续方程,从而可加快单个迭代步中的收敛速度,总体效率比较高。多相流的相界面追踪采用VOF方法,界面重构采用几何界面重构方法(Geo-Reconstruct)。 数值模型的计算网格划分采用非均匀网格,溢油喷口处及壁面处网格较密,网格总数为101 800个。计算区域长(x方向)200 m,深(y方向)20 m。溢油喷口宽0.1 m,沿x方向划分2个网格,单元网格尺寸为0.05 m;溢油喷口左右各设置2 m的网格加密区,沿x方向划分18个网格,单元网格尺寸从溢油口边界开始由0.05 m等比变化至0.2 m;从坐标轴原点O沿x轴至网格加密区左边界,距离为48 m;其他区域x和y方向的网格单元尺寸均设置为0.2 m。溢油模型计算网格划分如图2所示,其中图2(a)是计算模型整体网格划分图,图2(b)是溢油喷口附近加密的非均匀网格区域。 图2 溢油模型计算网格划分Fig. 2 The computational meshing for the oil spilling model 模拟计算中时间步长选为0.01 s,步长总数为12 000步,计算时长120 s。控制误差选用各方程残差的最大值, 控制精度为1×10-4。 为了便于分析,引入两个无量纲参数:溢油口密度弗劳德数Fr0和溢油初始速率与水流速率之比R0。其表达式为: Fr0表征了浮射流原动力中惯性力和浮力的相对比值。这二者的比例对浮射流(溢油)运动起决定性作用。R0表征了溢油初始速率和水流速率相对大小,该值变化对溢油轨迹的影响可反映出水流的作用。 Fan于1967年进行了浮射流实验,给出了不分层流动环境下垂直浮射流轨迹实验值[19]。之后的大部分海底溢油数值模型都将其作为验证的数据资料[3-4,10,17,20]。Yapa等[2]和Zheng等[10]基于Lagrangian积分法,建立了一个比较完善的溢油数值模型,该模型是许多后续研究的基础[3]。 采用k-ε紊流模型对多相流体运动控制方程进行求解,通过溢油体积分数云图来对溢油轨迹进行分析。追踪多相流界面所采用的方法是流体体积法(VOF方法),通过构造溢油体积分数函数F来追踪每个控制体内的溢油流量,并根据其函数值和导数值构造油水界面形状。在通过有限体积法(FVM方法)离散计算得到数值结果后,对结果进行后处理,将海水作为第一相、溢油作为第二相进行分析,设置合理的云图变量、色相频带来提高油、水两相界面间的区分度与清晰度。 图3 海底输油管道溢油体积分数和轨迹与实验值及数值模拟值的对比情况Fig. 3 Comparison of the trajectories between the present model and the experimental and numerical data 判断油膜分布是参照溢油体积分数,对于所分析区域,当溢油体积分数为0时,该部分为水;溢油体积分数为1时,则为纯油;当溢油体积分数介于0与1之间时,则为油水混合物。文中在分析时,对于溢油体积分数大于0.05阈值的区域,认定为油膜扩散区域。 图3给出了本模型的模拟结果和Fan实验值[19]、Zheng和Yapa数值模拟值[10]的对比情况,包括三种不同工况:(a)Fr0= 20,R0= 4;(b)Fr0= 20,R0= 8;(c)Fr0= 18.479 7,R0= 12.048 2。图3左列图为不同工况下溢油体积分数与Fan实验轨迹点的对比情况,右列图为溢油轨迹与Fan实验值[19]、Zheng和Yapa数值模拟值[10]的对比情况。从图中可以看出,本模型溢油的体积分数与实验轨迹点吻合很好,基本一致;较之Zheng和Yapa的数值模拟值[10],本模型模拟值更接近实验值。通过与实验值及数值模拟值的对比验证,证明本文所建立的模型是可靠的,用以模拟海底输油管道溢油运动轨迹是有效正确的。 模拟计算中各种参数选取主要参考渤海某油田群总体开发方案报告,根据其中提供的参数条件进行初步计算与分析,相关溢油参数的取值范围如表1所示。 表1 渤海某油田群溢油相关参数的取值范围Tab. 1 Ranges of spill related parameters in a Bohai oil filed 原油的溢出速度表征了溢油的初始动量。本节对原油的溢出速度进行了敏感性分析,研究了不同原油溢出速度对不同时刻溢油轨迹、到达海面时间、横向漂移距离和海面扩散范围的影响。针对海流速度0.1 m/s、溢出孔径0.1 m和原油密度844 kg/m3的工况,选取了5种不同的溢出速度2、4、6、8、10 m/s,计算区域水深取20 m。 3.1.1 不同时刻溢油轨迹对比 当原油从喷口溢出后,溢油轨迹的跟踪是研究的重点。图4为5种不同溢出速度情况下溢油轨迹的对比情况,分别比较了t=10、30、60、120 s等4个不同时刻,每个时刻5幅不同的图片分别对应于5种不同的溢出速度,从上至下,溢出速度依次增大。 从图中观察发现,随原油溢出速度不断增大,溢油在海面以下传播速度明显增大,且其连续性也逐渐增强,传播逐渐稳定后在海面以下形成长条连续的油带。t=10 s时,在最低流速(uoil= 2 m/s)情况下溢油刚到达计算海域的1/2时,最高溢出速度(uoil= 10 m/s)下的溢油已经逐渐接近海面(图4(a))。 t=30 s时(图4(b)),不同溢出速度情况下的溢油均已经到达海面,且溢油主体在横向流动的海流作用下向右倾斜、向上传播,小部分溢油在自由漂移作用下在海面向左侧传播;在溢出速度较小情况下,溢油在海面主要以零散的油滴和油块的形式分布存在,而当溢出速度逐渐增大,海面上大面积连续的油团和油带则逐渐增多。从t=60 s和120 s的溢油轨迹可以看出(图4(c)、(d)),此时溢油在海面下的传播形态已经相对比较稳定;随溢出速度增大,溢油在海面上扩散面积逐渐增大。 另外,从溢油轨迹图可以观察到,溢油在上浮过程中大致可分为以下5个阶段:1)当原油从破损孔口溢出瞬间,由于此时溢油仅受初始动量作用,此时加速度最大、速度相对较小,因此其在初始动量作用下形成纯射流,竖直流入海水中;2)原油从破损孔口溢出后,在初始动量、有效重力(浮力与重力之差)与海流联合作用下形成浮射流,浮射流过程中油滴的加速度逐渐减小、但是其速度不断变大;3)当溢油向上作用到一定程度,初始动量逐渐消失,形成羽流,在有效重力与摩擦阻力情况下,油滴的加速度逐渐减小至零,当加速度为零时,此时的溢油速度在整个扩散过程中是最大的;4)油滴逐渐接近自由海面,在溢出海面的过程中,由于界面张力的作用,能量消耗巨大,油滴速度急剧下降并且破碎;5)溢油到达海面之后,处于相对平衡状态,主要在海流作用下漂移扩散。 图4 不同原油溢出速度情况下溢油轨迹的对比Fig. 4 The trajectory of the spilled oil under different crude oil spilling velocities 3.1.2 到达海面时间对比 图5 不同原油溢出速度情况下溢油到达海面时间的对比及线性拟合结果Fig. 5 Arriving time of spilled oil to the sea surface under different crude oil spilling velocities and the linear fitting result 图5为不同原油溢出速度情况下溢油到达海面时间Ta的对比情况。从图中可以看出,随原油溢出速度逐渐增大,溢油到达海面时间逐渐减小,总体趋势接近线性分布(曲线拟合优度Adj. R-Square为90.83%,拟合公式为y= 28.9-1.55x),其最大差值约为51.9%;在目前选定的5种不同溢出速度情况下,溢油到达海面时间在10 s到30 s的时间范围之内。 3.1.3 横向漂移距离对比 溢油横向漂移距离指原油从泄露孔径溢出后在水下和海面上扩散漂移瞬间,最左和最右侧油膜距溢油孔径中心处的最大距离。在本文模拟计算中,海流由左向右传播,因此在实际分析中,该距离为计算海域中最右侧的油膜距溢油孔径中心处的距离。此处,水下特指从海面以下2 m到海床的海域,溢油孔径中心处的x坐标为50.05 m。图6为不同原油溢出速度情况下溢油横向漂移距离的对比情况,分别比较了t=60 s和120 s两个不同时刻,其中图6(a)为水下横向漂移距离Ldu,图6(b)则为海面横向漂移距离Lds。 图6 不同原油溢出速度情况下溢油横向漂移距离的对比Fig. 6 The lateral drifting distance of the spilled oil under different crude oil spilling velocities 从图6中可以看出,随原油溢出速度逐渐增大,无论在水下还是在海面上,溢油横向漂移距离均逐渐增大,且其距离从t=60 s到t=120 s是随时间增大的。在t=60 s和120 s两个不同时刻,水下溢油的横向漂移距离最大差值分别为45.7%和43.5%,海面溢油的横向漂移距离最大差值分别为45.1%和41.7%。 在相同溢出速度和相同时刻处,海面溢油横向漂移距离总是大于溢油在水下的横向漂移距离,这说明溢油在海面漂移比在水下扩散要传播得快;在t=60 s时,溢油在水下和海面上的横向漂移距离增长率相差不大,而在t=120 s时,溢油在海面上的横向漂移距离增长率明显大于其在水下的增长率,在最大溢出速度处海面溢油接近右侧边界。 图7 不同原油溢出速度情况下溢油海面扩散范围的对比及线性拟合结果Fig. 7 The surface diffusion range of spilled oil under different crude oil spilling velocities and the linear fitting result 3.1.4 海面扩散范围对比 海面扩散范围是指海面上油膜左、右两侧端点之间的距离。图7为不同原油溢出速度情况下溢油海面扩散范围Ad的对比情况。从图中可见,溢油海面扩散范围随原油溢出速度的变化情况与横向漂移距离随溢出速度的变化趋势基本一致,随原油溢出速度逐渐增大,溢油海面扩散范围逐渐增大,接近线性分布(t=60 s和t=120 s时刻曲线拟合优度Adj. R-Square分别为99.92%和97.41%,拟合公式分别为y= 43.79+7.64x和y= 103.35+9.44x),在t=60 s和t=120 s两个不同时刻其最大差值分别为51.0%和39.2%。此外,从t=60 s到t=120 s,溢油海面扩散范围随时间增大而增大。 不同的环境水深决定了原油从海底输油管道溢出后在海面以下传播的距离和时间的长短。针对这种情况,就原油溢出速度6 m/s、海流速度0.1 m/s、溢出孔径0.1 m和原油密度844 kg/m3的工况进行了计算。选取了5种不同的环境水深,其值分别是10、20、30、40、50 m,研究其对溢油传播轨迹、到达海面时间、横向漂移距离和海面扩散范围的影响。 3.2.1 不同时刻溢油轨迹对比 图8为不同环境水深情况下溢油轨迹的对比情况,分别比较了10、30、60、120 s等4个不同时刻的溢油情况。从图中可以发现,在不同水深情况下,溢油的传播轨迹与形态基本相同。 由于溢出速度相同,溢油在浅水深情况下更快传播到海面;最浅水深(h= 10 m)下的溢油在t=10 s时就已到达海面并在海面横向传播(图8(a))。在t=30 s和60 s时(图8(b)、(c)),不同水深、相同时刻下,水深越浅,溢油在海面的横向漂移距离和扩散范围越大。而在t=120 s时(图8(d)),由于溢出时间过长、趋近饱和,水深对溢油的敏感性降低,此前在水下横向传播的部分溢油通过纵向扩散也传播到了海面,因此不同水深下溢油在海面的横向漂移距离和扩散范围较为接近。 图8 不同环境水深情况下溢油轨迹的对比Fig. 8 The trajectory of the spilled oil under different environmental water depths 3.2.2 到达海面时间对比 图9为不同环境水深情况下溢油到达海面时间Ta的对比情况。 图9 不同环境水深情况下溢油到达海面时间的对比及线性拟合结果Fig. 9 The arriving time at the sea surface of spilled oil under different environmental water depths and the linear fitting result 从图中可以看出,随环境水深增大,溢油到达海面时间逐渐增大,且其变化接近线性分布(曲线拟合优度Adj. R-Square为99.39%,拟合公式为y= -3.1+1.13x)。不同水深之间溢油到达海面时间最大差值高达84.6%。 3.2.3 横向漂移距离对比 图10为不同环境水深情况下溢油横向漂移距离的对比情况。图中h/D、Ldu/D、Lds/D分别为无因次化后的水深、溢油在水下的横向漂移距离以及在海面的横向漂移距离,其中D为溢油孔径。从图中可以看出,在t=60 s和t=120 s两个不同时刻,随环境水深增大,溢油到达海面时间呈现不同的趋势。 当t=60 s时,在不同环境水深下,水下溢油横向漂移距离较为接近(最小差值仅为0.4%,最大差值为19.0%);而海面溢油横向漂移距离则随环境水深增大逐渐减小(最大差值为31.6%)。这是由于在相同溢出速度情况下,相同时间内、不同水深下溢油量相同,在横向海流作用下其在水下横向传播速度也基本相同,因此不同水深下水下溢油横向距离接近;而水深越深,溢油传播到海面的时间则越长,当总体时间一定,传播到海面的溢油量则越少,其在海面横向漂移的时间也越短,因此溢油在海面的横向漂移距离随水深增大而呈总体减小的趋势。而当t=120 s时,在水下,由于水深越深,溢油在水下传播的时间越长,其在水下累积量也越多、溢油在水下的横向漂移量也随之增大,因此随环境水深增大,水下溢油横向漂移距离其总体趋势逐渐增大,其最大差值为47.9%;而对于此刻的海面溢油,由于溢出时间过长、趋近饱和,水深对溢油的敏感性降低,此前在水下横向传播的部分溢油通过纵向扩散也传播到了海面,因此不同水深下溢油在海面的横向漂移距离较为接近,t=120 s时不同水深最小差值仅为1.5%,最大差值也仅为14.2%。 在相同水深、同一时刻,溢油在海面的横向漂移距离总是要大于其在水下的横向漂移距离。这说明溢油在海面的传播速度要比其在水下的扩散速度快。 图10 不同环境水深情况下溢油横向漂移距离的对比Fig. 10 The lateral drifting distance of the spilled oil under different environmental water depths 3.2.4 海面扩散范围对比 图11 不同环境水深情况下溢油海面扩散范围的对比Fig. 11 The surface diffusion range of the spilled oil under different environmental water depths 图11为不同环境水深情况下溢油海面扩散范围的对比情况。图中h/D、Ad/D分别为无因次化后的水深与溢油在海面的扩散范围。从图中可见,溢油海面扩散范围随环境水深的变化情况与海面横向漂移距离随水深的变化趋势基本一致。在t=和t=120 s两个不同时刻,随环境水深增大,溢油海面扩散范围呈现不同的趋势。 在t=60 s时,随环境水深增大,溢油海面扩散范围减小,这可归因于在相同溢出速度情况下,相同时间内、不同水深下溢油量相同,水深越深,溢油传播到海面的时间越长,当总体时间一定,传播到海面的溢油量则越少,其在海面横向漂移的时间也越短,因此溢油海面扩散范围随水深增大而减小;而在t=120 s时,由于溢出时间过长、趋近饱和,水深对溢油的敏感性降低,此前在水下横向传播的部分溢油通过纵向扩散也传播到了海面,因此不同水深下溢油在海面的扩散范围较为接近,此时不同水深间溢油扩散范围最小差值仅为1.5%,最大差值也仅为14.2%。 基于有限体积法,采用k-ε紊流模型,结合追踪多相流界面的VOF方法,对恒定海流作用下、海底输油管道溢油扩散进行了数值模拟研究,得到主要结论如下: 1)模型模拟结果与Fan的实验值吻合很好,证明了数值模型的可靠性。 2)溢油在水下的传播会形成一定的漩涡,在初始阶段主要以油滴和油块的型式进行传播,稳定之后其连续性会增强。 3)随原油溢出速度增大,溢油到达海面时间逐渐减小,总体趋势接近线性分布;对于20 m水深,在目前选定的5种不同溢出速度情况下,溢油到达海面时间在10 s到30 s的范围之内;溢油横向漂移距离与海面扩散范围随溢出速度增大均逐渐增大,接近线性分布。 4)随环境水深增大,溢油到达海面时间逐渐增大,接近线性分布。当t=60 s时,不同水深之间水下溢油横向漂移距离较为接近;而海面溢油横向漂移距离与扩散范围则随环境水深增大逐渐减小。当t=120 s时,随水深增大,水下溢油横向漂移距离其总体趋势逐渐增大,而海面溢油横向漂移距离与扩散范围在不同水深下则较为接近。 [1] 深水水下应急维修调研报告[R]. 天津:海洋石油工程股份有限公司, 2015. (The survey report for the deep-water emergency maintenance [R]. Tianjin: National Science and Technology Major Project 27-005-001-003-RPT-GE-001, 2015. (in Chinese)) [2] YAPA P D, ZHENG L. Simulation of oil spills from underwater accidents I: Model development [J]. J. Hydraul Res, 1997, 35(5): 673-687. [3] 汪守东. 基于Lagrange追踪的海上溢油预报模型研究[D]. 大连: 大连理工大学, 2008. (WANG Shoudong. Study on the forecast models for oil spills in seas based on Lagrange tracking [D]. Dalian: Dalian University of Technology, 2008. (in Chinese)) [4] HIRST E. Buoyant jets with three-dimensional trajectories [J]. J Hydraulics Division, 1972, 98(11): 1999-2014. [5] MCDOUGALL T J. Bubble plumes in stratified environments [J]. J Fluid Mech, 1978, 86(4): 655-672. [6] FANNELOP T K, SJOEN K. Hydrodynamics of underwater blowouts [J]. Norwegian Maritime Research, 1980, 4:17-33. [7] MILGRAM J H. Mean flow in round bubble plumes [J]. J Fluid Mech, 1983, 133: 345-376. [8] FANNELOP T K, HORSCHBERG S, KUFFER J. Surface current and recirculating cells generated by bubble curtains and jets [J]. J Fluid Mech, 1991,229: 629-657. [9] BEMPORAD G A. Simulation of round buoyant jet in stratified flowing environment [J]. J Hydraul Eng, 1994, 120: 529-543. [10] ZHENG L, YAPA P D. Simulation of oil spills from underwater accidents II: Model verification [J]. J Hydraul Res, 1998, 36(1): 117-134. [11] JOHANSEN O. DeepBlow-a lagrangian plume model for deep water blowouts [J]. Spill Sci Technol Bulletin, 2000, 6(2): 103-111. [12] ZHENG L, YAPA P D, CHEN F H. A model for simulating deepwater oil and gas blowouts Part I: Theory and model formulation [J]. J Hydraul Res, 2003, 41(4): 339-351. [13] 王晶. 海底管线溢油在水体中的运移扩散过程研究[D]. 大连: 大连理工大学, 2006. (WANG Jing. The study of the spread and diffusion process of oil spilled from seabed pipeline [D]. Dalian: Dalian University of Technology, 2006. (in Chinese)) [14] 高清军. 多种海况下的水下溢油数值模拟[D]. 大连: 大连海事大学, 2009. (GAO Qingjun. Numerical simulation of the underwater oil spill under a variety of sea conditions [D]. Dalian: Dalian Maritime University, 2009. (in Chinese)) [15] LI Wei, PANG Yongjie, LIN Jianguo, et al. Computational modeling of submarine oil spill with current and wave by FLUENT [J]. Res J Appl Sci Eng Technol, 2013, 21: 5077-5082. [16] ZHU Hongjun, LIN Pengzhi, PAN Qian. A CFD (computational fluid dynamic) simulation for oil leakage from damaged submarine pipeline [J]. Energy, 2014, 64: 887-899. [17] 陈海波, 安伟, 杨勇, 等. 水下溢油数值模拟研究[J]. 海洋工程, 2015, 33(2): 66-76. (CHEN Haibo, AN Wei, YANG Yong, et al. Numerical simulation of underwater oil spill [J]. The Ocean Engineering, 2015, 33(2): 66-76. (in Chinese)) [18] REN Bing, LI Xuelin, WANG Yongxue. An irregular wave maker of active absorption with VOF method[J]. China Ocean Eng, 2008, 22(4): 94-105. [19] FAN L N. Turbulent buoyant jets into stratified or flowing ambient fluids [R]. Pasadena, Calif.: W.M. Keck Laboratory for Hydraulics and Water Resources, California Institute of Technology, Rep. KH-R-18, 1967. [20] DONEKER R L, JIRKA G H. CORMIX1: An expert system for hydrodynamic mixing zone analysis of conventional and toxic single port aquatic discharges [R]. Washington: U.S. Environmental Protection Agency, 1990. Numerical simulation on the oil spill for the submarine pipeline based on VOF method LI Zhigang1, 2, 3, JIANG Meirong1, 2, 3, YU Jianxing2 (1. Offshore Oil Engineering Co., Ltd., Tianjin 300451, China; 2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China; 3. CNOOC Research Institute, Beijing 100028, China) P756.2; X55 A 10.16483/j.issn.1005-9865.2016.06.012 1005-9865(2016)06-0100-11 2016-01-14 工信部海洋工程装备科研项目(E-0815C003);中国博士后科学基金(2015M580203);国家自然科学基金重点项目(51239008) 李志刚(1965-),男,河北人,教授级高工,主要从事海洋工程方面的研究工作。 蒋梅荣。E-mail: meirongjiang@live.cn1.3 边界条件

1.4 离散方法和网格划分

2 数值模型验证


3 模拟结果分析

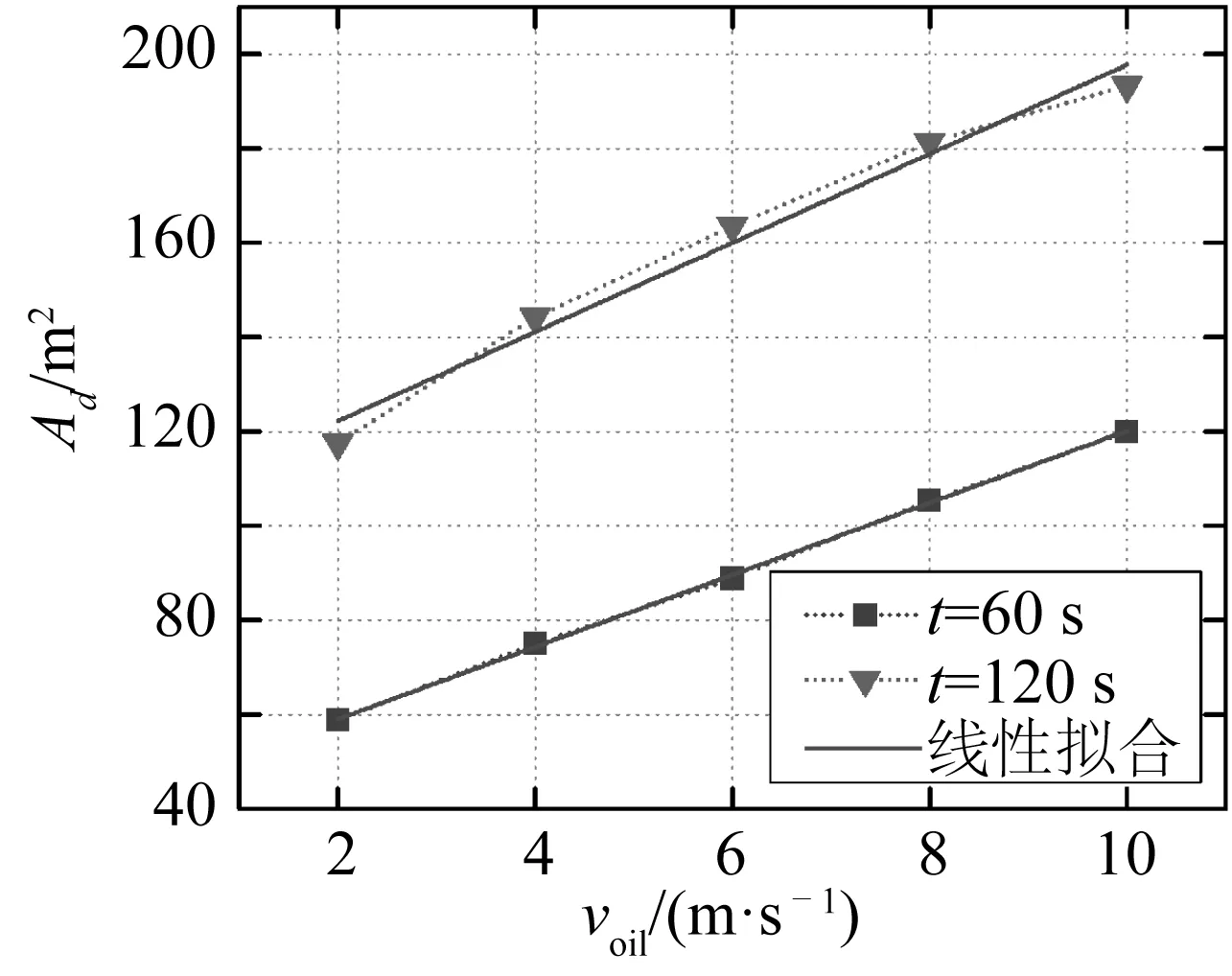
3.1 溢出速度的影响




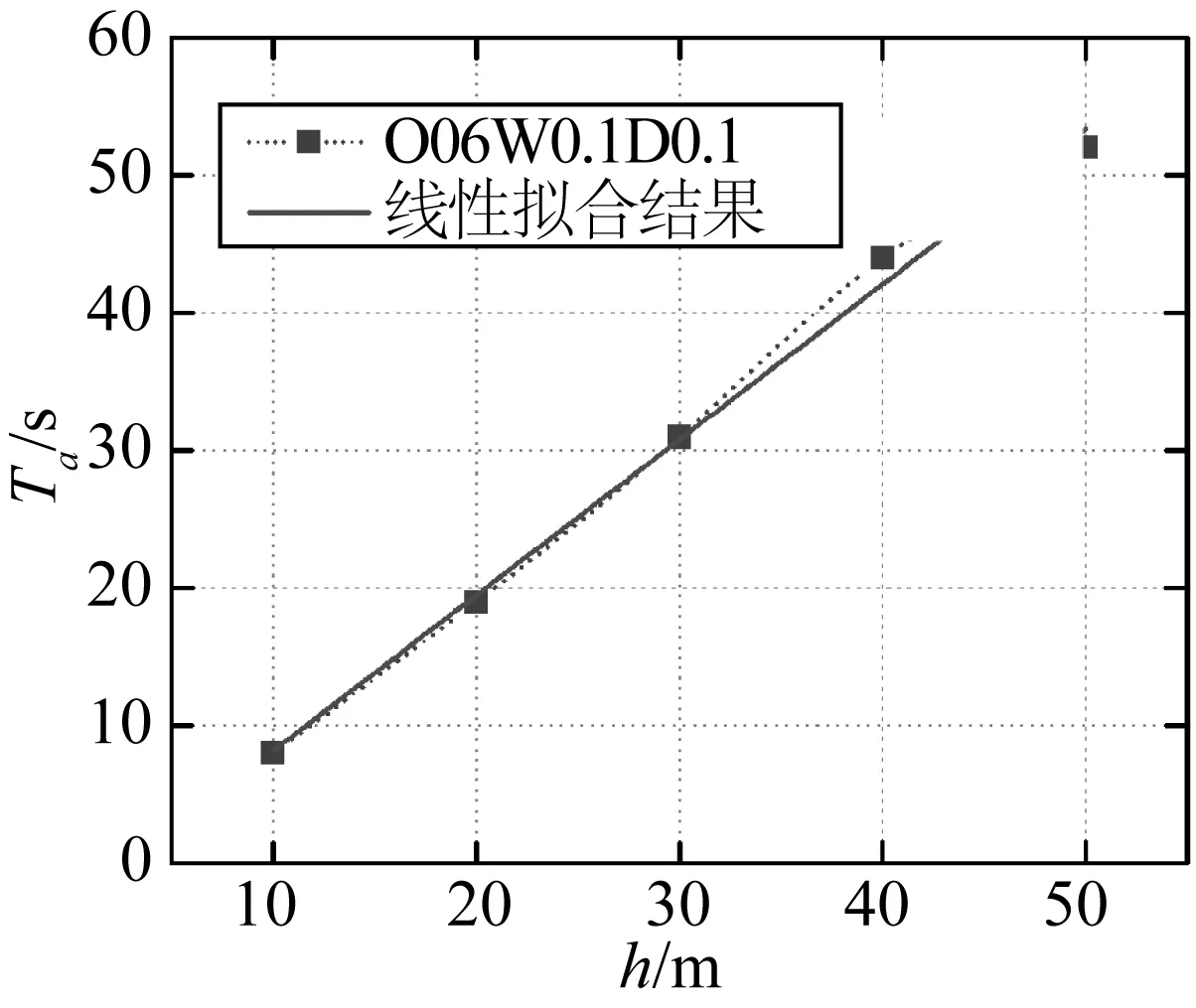
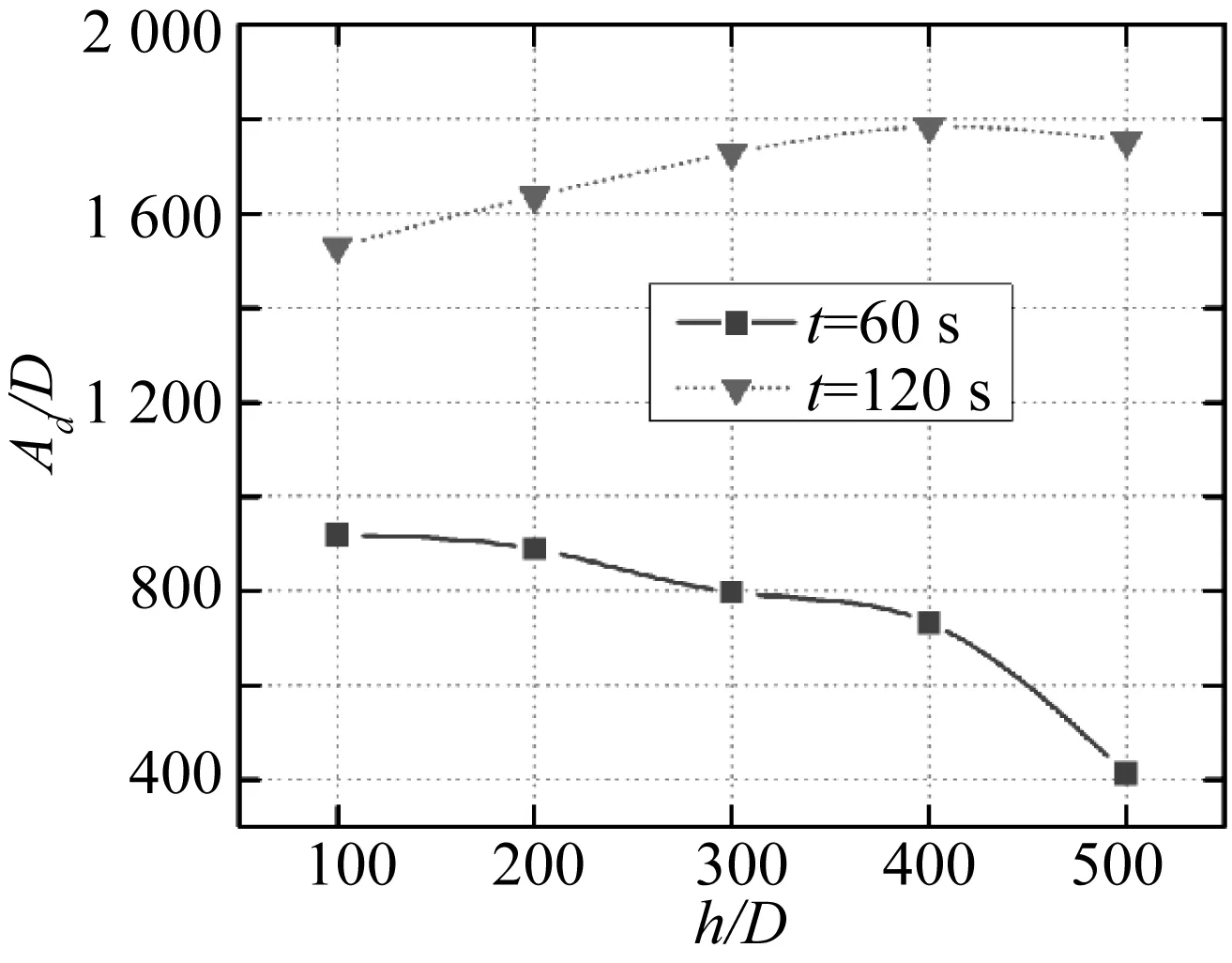
3.2 环境水深的影响


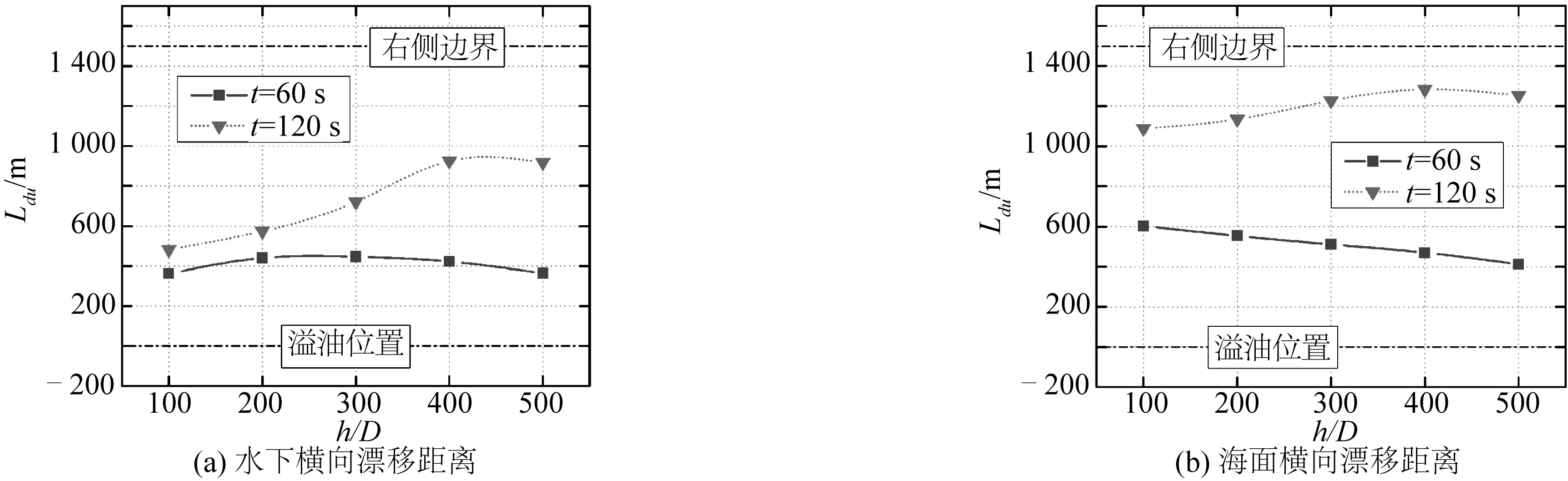
4 结 语

