集装箱船舶装箱排序问题优化模型及算法

, ,

(武汉理工大学 物流工程学院， 武汉 430063)

集装箱船舶装箱排序问题优化模型及算法

田维,张煜,程惠敏

(武汉理工大学物流工程学院，武汉430063)

针对现实约束下的船舶装箱排序问题，利用整数规划方法，以最小化横倾力矩为目标，构建该问题的数学模型。开发3阶段的启发式算法，基于规则构建预配载方案，进行集装箱互换，搜索优化解。对小规模案例和不同规模实际案例进行仿真试验，结果表明启发式算法均能在0.1 s内获得船舶实配约束下装箱排序问题的解。同时，通过与IBM ILOG CPLEX中分支定界算法的精确解求解情况进行对比，验证模型及优化算法的有效性和实用性。

装箱排序； 整数规划； 启发式算法； 分支定界算法

Abstract: In order to solve the sequencing and bin packing problem with practical vessel stowage constraints, a mathematical model of the problem is constructed based on integer programming method, which aims to minimizing the heel moment. A three-phase heuristics algorithm is developed, which makes a tentative stowage plan according to given rules first, and then find the optimum solution by interchanging containers. Simulations of actual stowage cases show that the problems can be solved within 0.1 s regardless the scale of the problem. Effectiveness and practicality of the model and optimal algorithm are verified through comparison with the exact solutions obtained by the branch & bound algorithm from IBM ILOG CPLEX.

Keywords: sequencing and bin packing problem; integer programming; heuristics algorithm; branch & bound algorithm

集装箱船配载是集装箱水上运输中的重要环节，对保障船舶的安全航行、货物的安全运输及运营的效率和效益有着很大的影响。因此，以集装箱装船后船舶的稳定性最优为目标研究港口集装箱的装船顺序和装载位置问题，避免后续在其他港口翻倒箱，实现有序装载，有着十分重要的意义。集装箱船舶装箱排序问题(Sequencing and Bin Packing Problem，SBPP)指的是集装箱堆场某个箱区贝内的集装箱按照一定的装船顺序发箱，并依次装船至船舶贝内具体箱位的问题。集装箱装船时，在考虑船舶稳定性的基础上，通过合理安排集装箱的装载顺序达到满足船舶贝内的积载强度、重不压轻、不存在阻塞箱、不悬空及不违背发箱顺序规律等现实约束的要求。SBPP是典型的NP-hard组合优化问题[1]，近年来已有一些学者对其进行研究。张维英等[2]对单一目的港贝位排序建立模型，采用禁忌搜索算法求解；孙晓雅等[3]建立模型研究多港贝位排序问题，并采用粒子群算法求解，但仅考虑避免后续港口翻倒箱，未考虑积载强度、质量及其他现实约束；王莉莉等[4]对装船顺序的优化过程建立模型，并采用遗传算法求解；孙俊清等[5]对多港口、多贝位的配载建立0-1规划数学模型，考虑船舶稳定性的约束，并用遗传算法求解；张维英等[6]在贝位配载中考虑舱盖分块，采用隐士图启发式搜索技术求解混装贝位的排箱优化模型；李坤等[7]建立多贝位的整数规划模型，将问题分为2个阶段，并采用禁忌搜索算法求解；MONACO等[8]建立最小化装船时间和翻箱的数学模型，但未对集装箱在堆场的发箱顺序及对配载的约束进行研究；DUBROVSKY等[9]考虑船舶单贝配载计划，以最小化翻箱次数为目标，利用遗传算法求解；DELGADO等[10]使用约束规划(CP)和整数规划(IP)建立模型并进行精确求解；MOURA等[11]将配载问题与船舶路径相结合建立数学模型，研究延伸到全航线的成本优化。

以上研究主要从贝内排箱问题的角度建立数学模型，采用禁忌搜索算法、粒子群算法、遗传算法和分支定界算法等算法进行求解，而未考虑堆场发箱顺序对船舶贝内排箱问题的影响。堆场贝内堆存状态较差及其装船发箱顺序不合理会导致船舶贝内生成阻塞箱，从而增加后续港口卸货时的翻倒箱数，不利于全航线的配载。对此，结合港口运作的实际经验和规则，建立符合实际的优化模型，设计有效的启发式算法，以满足港口实际配载的需要。

1 集装箱船舶装箱排序问题的优化模型

1.1 模型假设

考虑到堆场与船舶的实际运作情况，针对配载问题给出以下假设：

1) 集装箱堆场实际堆码按照PSCW规则实施，即同一个目的港、同一尺寸、同一种类的集装箱按照质量级别堆放在堆场的同一贝位内，一般重箱在上、轻箱在下。

2) 集装箱堆场内不同种类的集装箱不混装，危险品箱、冷藏箱等特殊箱与标准箱不在同一贝内摆放，这里仅考虑具有相同尺寸的标准集装箱。

3) 为提高堆场的作业效率，避免起重机小车无序行走，堆场贝内集装箱通常遵循港口实际操作经验逐列依次装船发箱(见图1)，可确定各个出口箱的发箱顺序。

图1 堆场发箱顺序

4) 集装箱堆场待装船箱区贝内的集装箱总数和质量小于船舶贝内的箱位数及允许的最大承重，保证堆场贝内所有待装船集装箱都能完成装载。

5) 为保证安全，集装箱船舶贝内实际配载需考虑任意列的集装箱积载强度要求，避免单列集装箱质量之和大于船舶局部载荷强度。

1.2 数学模型

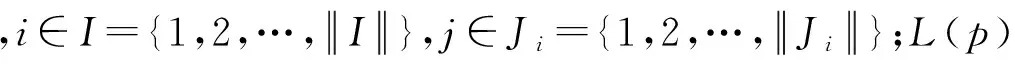
2) 决策变量为xkp，表示集装箱k是否装到船舶上的p箱位，为0-1决策变量。

3) SBPP问题优化模型为

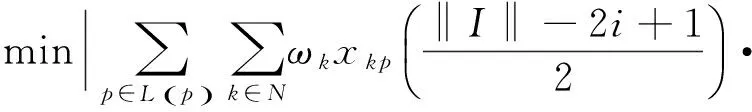
(1)

s.t.

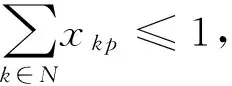
(2)

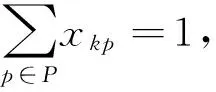
(3)

(4)

(5)

(6)

(7)

(8)

式(1)中：z为最小化船舶贝的横倾力矩，t·m；d(取2.438 m)为集装箱的宽度；Δ(取0.3 m)为相邻2个集装箱之间的间隙。由于集装箱船舶贝内的集装箱会对贝内横切面中心轴产生力矩，因此为避免船舶结构出现损伤，需控制贝内左右两边的力矩之差，即要求贝内横倾力矩越小越好。式(2)表示船舶贝内任意箱位最多放一个集装箱；式(3)表示一个集装箱必须占用一个船舶贝内箱位；式(4)表示船舶配载时集装箱不悬空；式(5)表示船舶装载时堆场先发箱不能置于后发箱的上面；式(6)表示船舶贝位单列的堆积约束；式(7)表示船舶配载中的质量等级约束，即重不压轻；式(8)表示船舶贝内避免形成阻塞箱。

2 集装箱船舶装箱排序问题算法设计

集装箱船舶装箱排序问题是NP问题，在装船量较小的情况下也是大规模的复杂优化问题，且随着问题规模的增大，求解时间成指数倍增长。由于大规模现实问题无法在现实时间要求范围内给出最优解，因此设计三阶段启发式算法对集装箱船舶装箱排序问题进行求解。

1) 第1阶段是预处理阶段。按照堆场贝内集装箱装船发箱规则确定各个集装箱的发箱顺序，按照发箱顺序排列形成待装船集装箱集合N，依次进行装船。在船舶贝中，按照自中间向左右两侧递增的方式对列进行优先级定义，自下而上对层进行优先级定义。对每列按照层的优先级形成空箱位集合，并初始化每列的当前载重TW。

2) 第2阶段是预配载阶段。对待装船集装箱集合N中的所有集装箱进行装船操作。按照列、行的优先级顺序依次选取各集装箱的目标箱位，并对目标箱与紧挨目标箱位之下的箱位p′=(i,j-1)中所装载的集装箱k′进行质量等级、目的港的比较，以此检验是否能满足重不压轻、翻倒箱的约束；对目标箱的质量与该列当前所能承受的剩余负荷Si-Ti进行比较，以此检验是否能满足积载强度的约束。依次将集装箱装船，完成所有集装箱的装载，得到预配载方案。

3) 第3阶段是横倾优化阶段，包括列交换和箱位交换2部分。

(1) 对第2阶段得到的预配载方案进行列交换操作。在相同大小的列集合中互换所有列，并计算相应的横倾力矩。

(2) 选择最小横倾力矩的列交换方案进行箱位交换操作。列出所有集装箱的箱位互换组合，并进行装箱顺序、质量等级、阻塞箱形成及列积载约束的判断，若满足约束，则进行箱位互换操作，并计算对应的横倾力矩。

(3) 根据计算结果得出横倾力矩值最小的箱位交换方案，输出该方案及最小的横倾力矩值，即为最终的配载方案。

基于上述3个阶段，启发式算法的流程见图2。

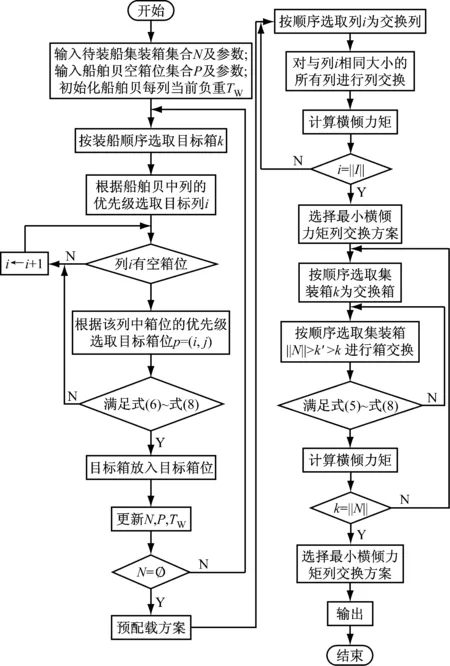
图2 三阶段启发式算法

3 仿真分析

利用MATLAB对所提出的启发式算法进行验证，所有结果均在Intel Core 42.4 GHz CPU及8G内存平台下测得。

3.1 小规模案例

集装箱堆场某个箱区贝内有24个集装箱，摆放成6列，挂靠3个目的港，其质量由Excel随机生成。这些集装箱待装载入某船舶贝，该船舶贝有7列6层，每一列允许的最大积载强度(单位为t)见图3，其中：堆场贝中方框表示集装箱；中间的数字表示提箱顺序；左下角的数字表示集装箱的质量；右上角的数字表示集装箱的目的港。

采用设计的启发式算法对案例进行求解，得出的最小横倾力矩为2.738 t·m。使用CPLEX软件对上述案例进行精确解求解，得出的最小横倾力矩为0，得出的配载方案见图4。从图4中可看出，利用启发式算法得到的解与利用CPLEX软件得到的精确解较为接近。

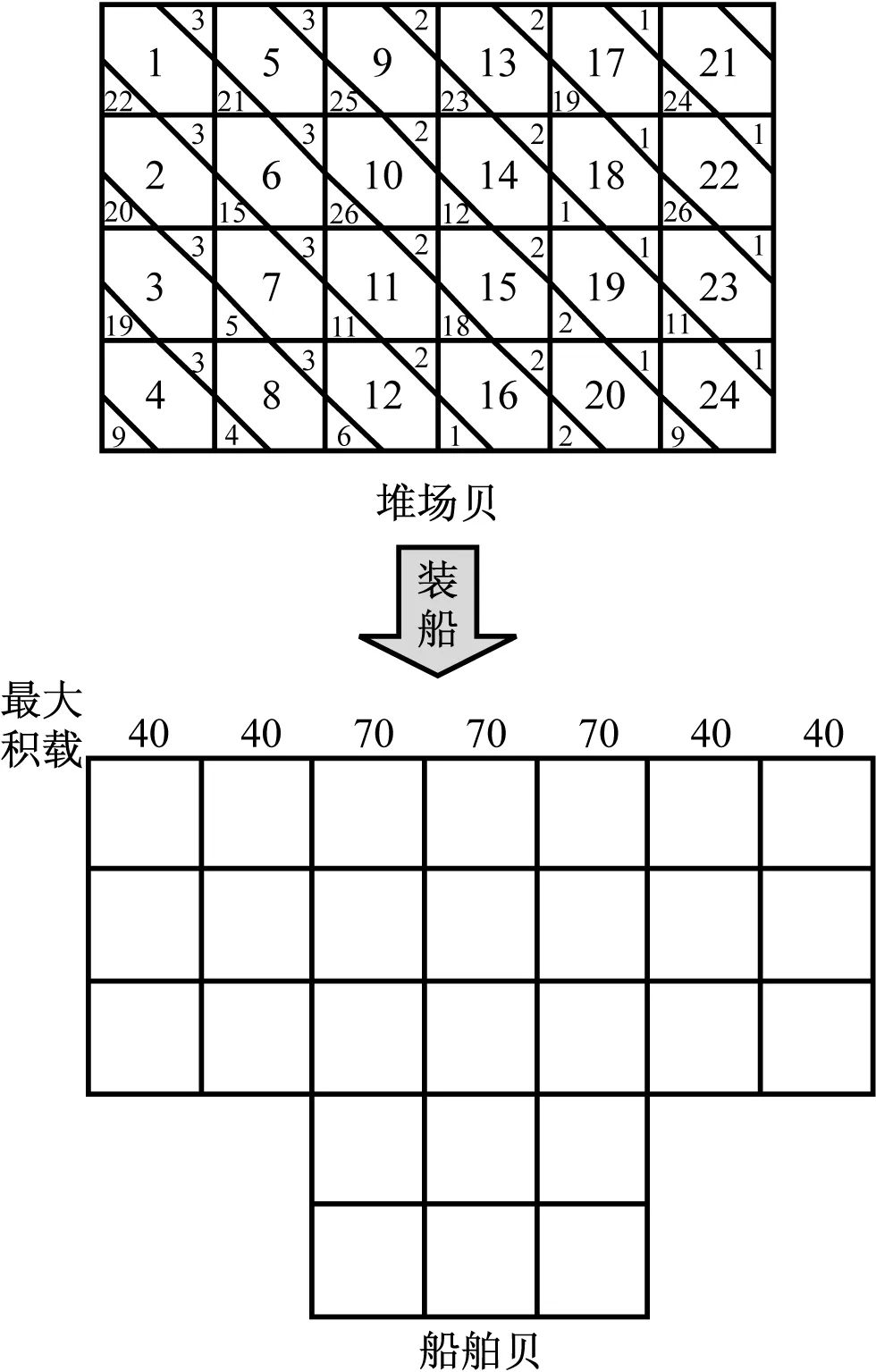
图3 小规模案例

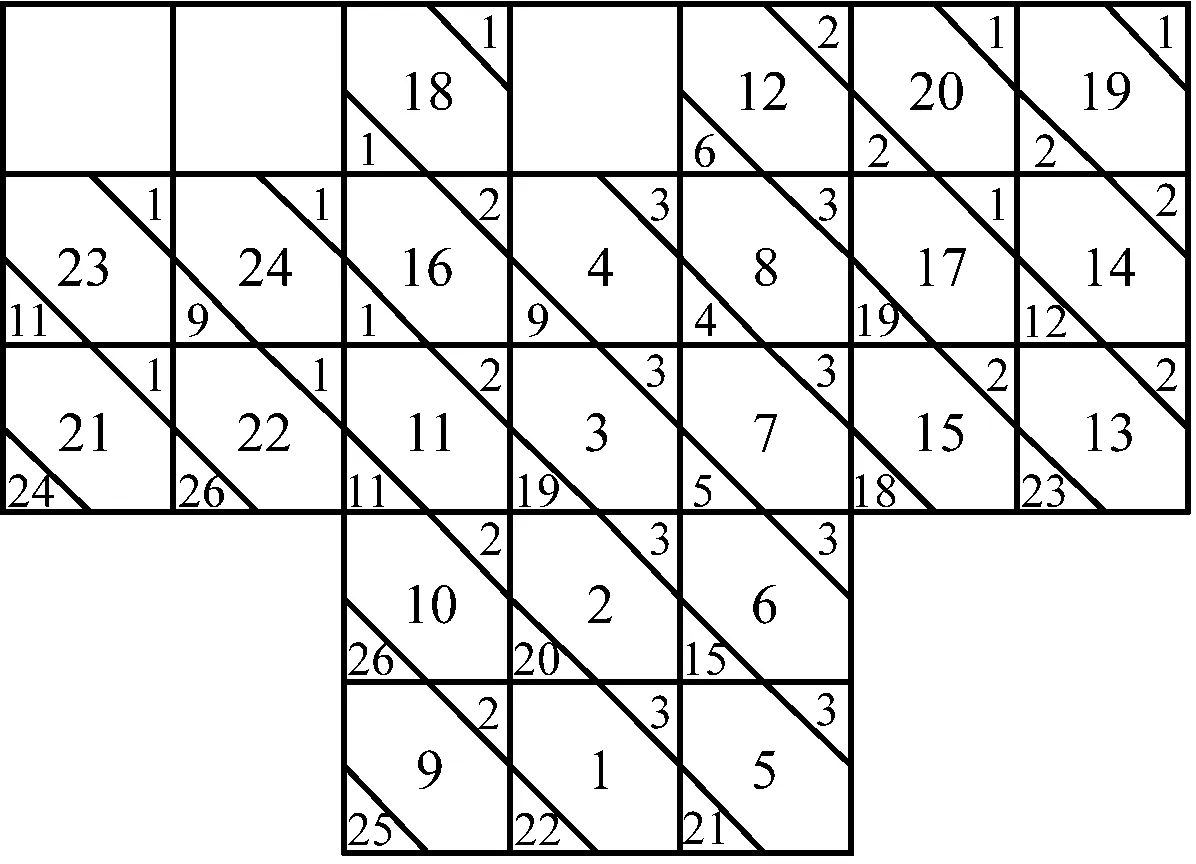
a) 启发式算法

b) CPLEX

船舶贝的最大允许横倾力矩计算式为

(9)

式(9)中：δ为力矩敏感系数。由该计算式可计算出该贝的最大允许横倾力矩MH(δ取5 t，相当于1个轻箱所导致的M偏差)为41.07 t·m。利用启发式算法得到的解也远低于MH，且该算法得到的配载方案在船舶贝的列上同一目的港的集装箱较为集中，这样有利于后续港口进行集装箱卸载操作。

3.2 实际案例

为进一步验证算法的有效性，结合某港某集装箱船舶的实际案例进行仿真分析。该港口待装载到该船舶有6个目的港，这里选取其中4个不同结构的贝进行案例求解(见图5)。

a)贝09b)贝17

c)贝45d)贝47

图5 船舶贝

将堆场中的36个集装箱(6列6层堆放)、48个集装箱(8列6层堆放)、66个集装箱(11列6层堆放)和72个集装箱(12列6层堆放)分别装载到贝09(最大允许承重为640 t)、贝17(最大允许承重为780 t)、贝45(最大允许承重为1 000 t)及贝47(最大允许承重为1 060 t)中。在每个场景下进行5个随机案例的仿真试验，使用设计的启发式算法及CPLEX中的分支定界算法求解,结果见表1，其中*表示案例在2 h内无计算结果。

由表1可知，设计的启发式算法在不同规模的不同案例下均能得到与精确解较为接近的解，个别情况下与精确解相同，解的质量较高。对于规模较大的现实问题，CPLEX大部分案例在有效时间内不能得到解，少数案例虽能得出精确解，但求解时间较长；而启发式算法运算速度极快，能在0.1 s内求解，远远超过实际应用的需求，具有良好的实用性。

3.3 算法性能分析

为评估三阶段启发式算法的性能，结合问题的上、下界理论定义算法性能的间隙公式，即

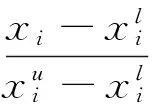
(10)

数据分析结果见表2，利用启发式算法在不同场景下得到的间隙值G最大为5.82%，最小为2.91%，这表明利用三阶段启发式算法所得解的质量较高，能满足实际装船时对横倾安全性的要求，可在有效时间内解决现实情况下的集装箱船舶装箱排序问题。

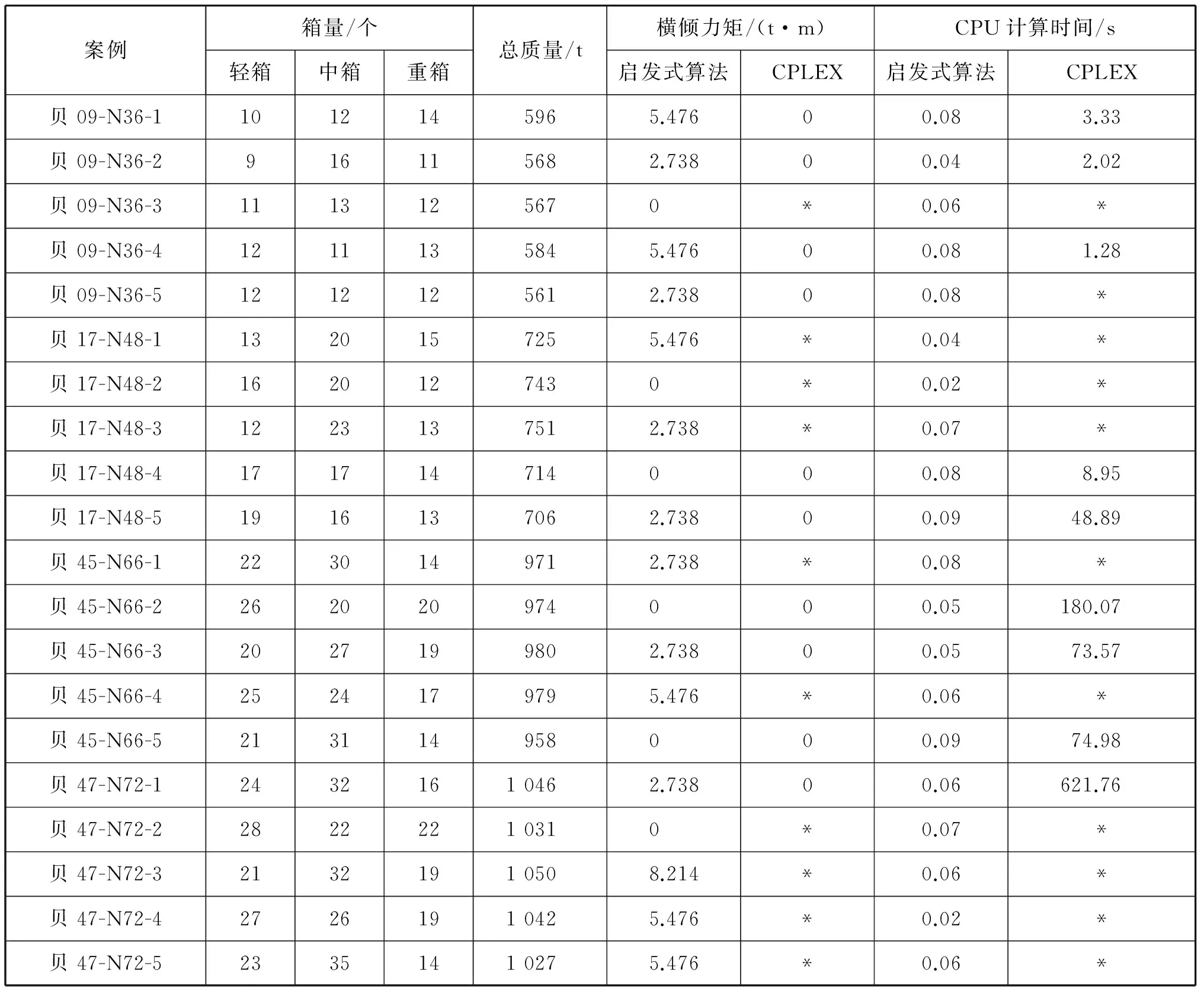
表1 案例的数据处理结果

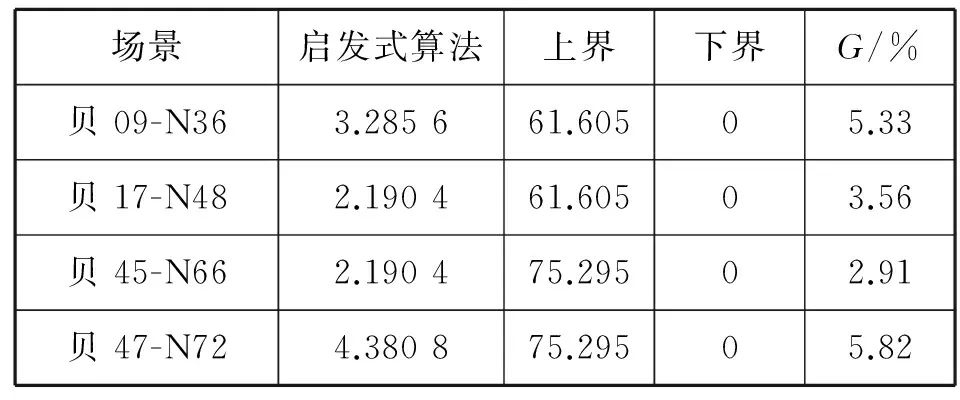
表2 数据分析结果

4 结束语

针对堆场某个箱区贝内的集装箱装载到船舶某个贝位确定位置的装箱排序问题，提出解决方案，并基于横倾力矩最小化的目标与现实约束构建该问题的混合整数规划模型。该模型可保证船舶在安全性最优的情况下完成配载，且可避免形成阻塞箱。此外，进一步开发了三阶段的启发式算法，通过现实案例验证了模型及算法的有效性和实用性。

[1] 黎明,翟金刚.集装箱装船顺序的多目标整数规划优化模型[J].计算机应用研究,2012,29(10):3635-3639.

[2] 张维英,林焰,纪卓尚,等.基于指派问题的Bay位排箱优化模型与算法[J].大连理工大学学报,2011,51(1): 61-67.

[3] 孙晓雅,林焰.集装箱船多港Bay位排箱的优化方法[J].大连海事大学学报,2011,37(1): 75-79.

[4] 王莉莉,于红.集装箱装船顺序优化模型及遗传算法[J].计算机工程与应用,2008,44(5):234-238.

[5] 孙俊清,陈忱,刘凤连.考虑船舶稳定性的多港口集装箱配载问题[J].计算机工程与应用,2012,48(32):236-243.

[6] 张维英,林焰,纪卓尚,等.集装箱船全航线Bay位排箱优化模型[J].上海交通大学学报,2007,41(2): 48-53.

[7] 李坤,唐立新.集装箱码头装船计划问题建模与优化研究[J].控制工程,2015,22(4): 683-689.

[8] MONACO M F, SAMMARRA M, SORRENTINO G. The Terminal-Oriented Ship Stowage Planning Problem[J].European Journal of Operational Research,2014,239(1): 256-265.

[9] DUBROVSKY O, LEVITIN G, PENN M. A Genetic Algorithm with a Compact Solution Encoding for the Container Ship Stowage Problem[J]. Journal of Heuristics, 2002, 8(6):585-599.

[10] DELGADO A, JENSEN R M. A Constraint Programming Model for Fast Optimal Stowage of Container Vessel Bays[J]. European Journal of Operational Research, 2012, 220,(1):251-261.

[11] MOURA A, OLIVEIRA J, PIMENTEL C. A Mathematical Model for the Container Stowage and Ship Routing Problem[J].Math Model Algor, 2013,12(3):217-231.

Optimal Model and Algorithm of Sequencing and Bin Packing Problem for Container Carrier

TIANWei,ZHANGYu,CHENGHuimin

(School of Logistics Engineering,Wuhan University of Technology,Wuhan 430063, China)

1000-4653(2016)04-0118-05

U695.2+2

A

2016-07-25

国家自然科学基金(71372202)

田 维(1990—)，女，湖北荆州人，硕士生，从事物流系统建模与优化研究。E-mail: twaisy@126.com

张 煜(1974—)，男，天津人，教授，博士，从事智能决策、物流系统建模与仿真研究。E-mail: sanli@whut.edu.cn