多目标选择性拆卸序列优化问题的分散搜索算法
郭希旺,刘士新,王大志
(东北大学信息科学与工程学院,辽宁沈阳110819)
多目标选择性拆卸序列优化问题的分散搜索算法
郭希旺,刘士新,王大志
(东北大学信息科学与工程学院,辽宁沈阳110819)
针对多资源约束下顺序依赖的选择性拆卸序列优化问题,建立以最大拆卸收益和最小拆卸时间为优化目标的多目标数学模型,提出了一种多目标分散搜索优化算法进行求解.该算法针对本文问题的特点设计了一种保持足够多样性的初始解生成方法,满足拆卸优先关系的交叉组合算子以及改进的参考集更新策略.为了进一步提高解的质量设计了一种局域搜索策略,并利用外部存档方法存放Pareto解集.应用多组实例进行计算实验,并与其他求解该问题的算法进行比较,实验结果表明本文算法优于对比算法,证明本文模型和算法求解本类问题有效.
选择性拆卸序列优化;多资源约束;多目标;分散搜索算法
1 引 言
近年来,由于拆卸序列优化问题的理论研究和实际应用价值,已经引起了国内外很多学者的研究和关注,提出了一些数学模型和优化算法.文献[1]提出拆卸可行信息图描述产品拆卸序列操作信息,拆卸序列规划问题被映射到拆卸可行信息图作为一个路径搜索问题,并采用遗传算法求解.文献[2]提出一个拆卸优先图来表示产品结构并通过迭代法求解问题.文献[3]提出分散搜索算法解决复杂产品拆卸序列优化问题.文献[4]提出了基于规则的目标选择拆卸方法.文献[5]基于装配方法建立了与或联络图,产生了包含目标零部件的全部可能拆卸序列,并利用筛选过程选择最优序列.文献[6]采用混合图对目标拆卸序列进行分析,并应用遗传算法进行优化.文献[7]考虑了零部件的成批拆卸和工具的可达性,提出了一种集成的选择拆卸方法.文献[8]针对报废产品的选择性拆卸序列优化问题提出了一个进化算法.
上述文献在构建模型和算法时所考虑的目标均为单个目标,而实际的拆卸序列规划往往有多个目标,这些目标相互制约.此外,现有研究主要集中于无资源约束的问题,在实际拆卸零部件过程中,往往受到时间、劳动力、设备以及资金等多资源的约束.因此,有必要研究多资源约束下多目标拆卸序列优化问题.分散搜索算法在求解组合优化问题上体现出了良好的优化性能,但目前主要应用于单目标问题的求解,多目标分散搜索算法的研究相对较少.
本文研究了多资源约束下顺序依赖的选择性拆卸序列多目标优化问题(multi-objective multi-resourceconstrained sequence-dependent selective disassembly sequence optimization problems,MMSSDSOP).建立了以最小拆卸时间和最大拆卸收益为目标的多目标优化模型,根据模型特点设计了分散搜索(scatter search,SS)优化算法,算法可以针对本文问题求得高质量的Pareto解集.
2 问题描述及模型
2.1问题描述
MMSSDSOP可描述如下:在拟拆卸产品中,包含着J个零部件,每个零部件都用整数1,2,...,J来标记.以图1[9]中某产品的结构图为例,图中零部件的总数为8,实线箭头代表零部件之间的优先关系,箭头的指向为该零部件必须在箭尾零部件拆卸后才能够进行拆卸.相邻两个零部件拆卸成本和时间随着拆卸先后顺序的改变而改变.例如,图中零部件1必须在所有零部件前进行拆卸,零部件5和6必须在零部件8前进行拆卸.图中虚线箭头代表零部件之间的拆卸顺序依赖,指拆卸一个零部件时会受到另外一个零部件的阻碍.虚线箭头的指向为该零部件拆卸时受到虚线根部零部件阻碍.本文使用拆卸顺序依赖时间增量的概念[9],如果零部件j在零部件k之前进行拆卸,零部件j在零部件k的影响下拆卸时间产生增量(被迫延长).当一个零部件拆卸受到其他零部件拆卸顺序依赖时,该零部件的总的拆卸时间为拆卸该零部件所消耗的时间和受到其他零部件拆卸顺序依赖时间增量的总和.图中圆括号中的数字代表虚线弧的箭尾零部件对箭头指向零部件的拆卸顺序依赖时间.例如,对于一个给定的拆卸序列1,2,3,6,5,8,7,4,零部件2被拆卸在零部件3的前面,拆卸零部件2时受到零部件3的影响,其拆卸顺序依赖时间增量为四个时间单位.图中方括号[]里的数字代表拆卸该零部件所需要的资源数量,拆卸过程需要多种资源,拆卸方案必须满足各种资源的可用量约束限制.例如,图1描述的问题仅涉及1种资源,拆卸零部件1所需要的资源数量为[3],拆卸零部件2所需要的资源数量为[4].求解MMSSDSOP同时确定每个零部件是否拆卸以及拆卸顺序.
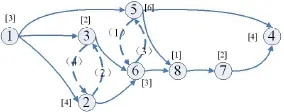
图1 产品结构图Fig.1 The structure diagram of product
MMSSDSOP的特点和难点如下:1)拆卸过程受到多种资源约束限制;2)拆卸过程中零部件之间存在相互依赖关系约束;3)该问题是一类排序与选择混合的复杂整数规划问题;4)具有两个优化目标,属于多目标优化问题.随着零部件、零部件间相互依赖的数量的增加、决策变量和约束的数量将迅速增加,计算和求解过程变得更加困难.因此,本文设计了求解该类问题的SS算法,以便求得高质量的Pareto解集.
2.2模型
基于上述问题描述,本文针对MMSSDSOP建立如下数学模型:
1)输入条件(问题参数)
J为产品中零部件个数,j,k=1,2,...,J代表零部件编号;
Rj为拆卸零部件j的收益;
DCj为拆卸零部件j的成本;
DTj为拆卸零部件j的时间;
rrjk为拆卸零部件j后拆卸零部件k的转换消耗资源r的数量,r=1,2,...,R;
srj为拆卸零部件j消耗资源r的数量,r=1,2,...,R;
Cr为资源r的最大可用量,r=1,2,...,R;
Cjk为拆卸零部件j后拆卸零部件k的转换成本;
ctjk为拆卸零部件j后立刻拆卸零部件k的转换过程需要的时间;
stjk为拆卸零部件k时零部件j对其的拆卸顺序依赖时间增量;
2)输出条件(决策变量)

3)约束条件:在拆卸零部件时受到一些条件的限制,以下是本文的约束条件.

其中式(1)代表变量之间的关联关系;式(2)代表拆卸一个产品受到资源的限制;式(3)代表两个相邻零部件最多只能执行一次转换;式(4)代表决策变量的取值范围.
4)目标函数

式(5)代表拆卸一个产品所获得的收益;式(6)代表拆卸一个产品所需要的时间.决策的目的是最大化拆卸收益,最小化拆卸时间.
3 求解算法
SS算法是一种元启发式算法,已被证明是求解复杂组合优化问题的有效方法.与其他元启发式算法一样,在应用中首先需要对解进行编码,然后按照算法实现步骤进行计算.SS算法基本流程主要由多样性初始解产生方法、子集产生方法、子集合并方法、解改进方法以及参考集更新方法5个部分组成[10].在SS基本流程基础上根据求解问题的不同可以采用不同的实现方式,这使得该算法具有很好的灵活性.
本文SS算法流程如下:

大量研究针对SS算法中的各组成部分作了很多有益的改进,对求解速度和求解效果有了很大的提高[11].下面介绍SS算法中的初始解集的产生、参考解集、组合算子、局域搜索算子和参考集更新五部分,它们是算法的核心.为了保证在求解过程中产生一个高质量的Pareto解集,采用外部存档管理方法[12].外部存档的主要目的是在搜索过程中记录存储每一个非支配个体.本文SS算法采用最大代数作为停止准则.
3.1解的编码和解码
MMSSDSOP是一类排序与选择混合的优化问题,因此,本文采用双链表结构对解进行编码.记个体sol=(sols,solx),其中sols=(s1,s2,...,sJ)表示拆卸零部件顺序,solx=(x1,x2,...,xJ),xi代表第i个零部件是否拆卸.以图1中的产品为例说明编码方式及目标函数的计算过程如下:图1所示产品包含八个零部件,各零部件的收益、拆卸成本、拆卸时间、每个零部件拆卸需要的资源数量和两个相邻零部件之间拆卸的转换时间和转换成本如表1,表2和表3所示.零部件拆卸时总的资源数量Cr=50,对该问题随机选择一个个体,sols=(1,2,3,5,6,8,7,4),solx=(1,1,1,1,1,1,1,1),解码后得目标函数值Z1=30,Z2=114.

表1 例1中的问题参数Table 1 Problem parameters in example 1
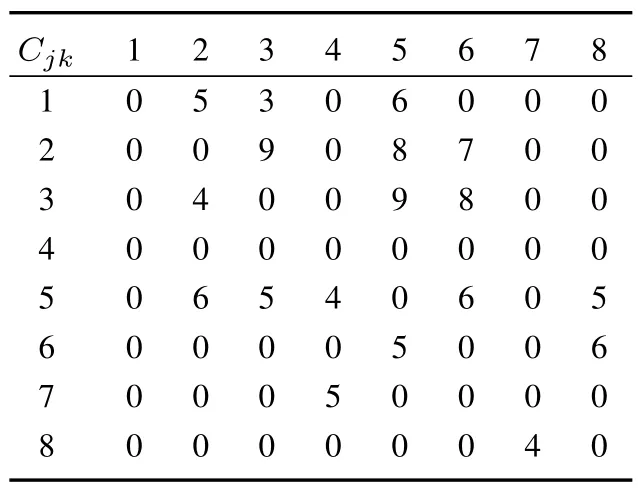
表2 例1中的转换成本Table 2 Transform cost in example 1

表3 例1中的转换时间Table 3 Transform time in example 1
3.2初始解集的产生
本文设置初始种群规模为P,根据双链表结构的编码,初始解的产生方法如下:1)随机产生一个满足优先关系的零部件拆卸序列sols=(s1,s2,...,sJ),即为初始解的sols链表;2)按照零部件si在sols中所处的位置,依次将与之对应的xi元素放置到solx中,xi是在0,1中随机产生的,形成solx链表;3)由于零部件拆卸过程中的依赖关系,经过过程1),2)产生的个体不一定可行,针对不可行个体按如下方式修改solx链表:一旦某个零部件si在solx中的值为“1”,那么零部件si的所有前驱节点值也为“1”;一旦某个零部件si在solx中的值为“0”,那么零部件si的所有后继节点的值要为“0”.重复1)~3)过程P次,可以产生初始种群.
3.3参考解集
参考集是高质量的解和多样性的解的集合.因本文问题优化目标有两个,因此,本文设计的参考集由3部分构成:1)在初始解集中选择b1个目标函数值Z1最大的解作为参考集中b1个高质量解;2)选择b2个目标函数值Z2最小的解作为参考集中b2个高质量解;3)为了产生b3个多样性解,本文定义了两个个体之间的距离,即
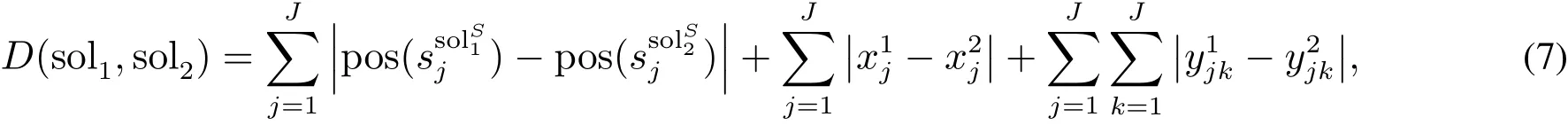
记Ref为当前参考集,soli/∈Ref,定义soli和Ref的距离为
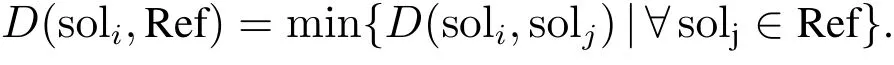
参考集中多样性解的产生方法就是从初始解中逐个地选择出b3个距离当前参考集Ref距离最大的解.
3.4组合算子
由于子集中的解来源于参考集Ref,因此,组合算子是将参考集中的优质解和多样性解组合成新解,合理设计组合算子既可以保证解的优质性又可以保证解的多样性.针对个体的双链表结构,本文基于PPX机制[13]设计如下组合算子:记参与PPX交叉运算的两个个体分别为组合生成的子代个体为,则组合算子流程如下:

3.5局域搜索算子
在SS算法中,经过组合算子生成的子代个体都将作为起始解经局域搜索算子进行改进.本文设计的局域搜索算子包含以下四个步骤:
步骤1针对个体的sols进行操作.在子代个体中随机选择两个个体,一个作为初始解另一个作为向导解,交换邻域从i=1开始,比较两个解访问的零部件是否相同,如果,继续访问下一个零部件;如果访问的零部件不相同,在起始解寻找与向导解访问相同的零部件,即,找到确定该位置j,然后将交换,其他零部件的访问顺序不变.i←i+1,开始下一阶段扫描;
步骤2针对个体的solx操作.对相应位值进行改变,如二进制编码中“0”变为“1”,“1”变为“0”.进而形成新的个体
步骤3可行化处理:根据问题的假设和模型的约束条件,经过步骤1和步骤2变换后的解不一定是可行解,因此,需要对每次迭代得到的新个体进行可行性判定,若可行则过程继续,否则需要进行解的可行化处理.处理的方法是,一旦某个零部件i在变换过程中solx的值由“0”变为“1”,那么零部件i的所有前驱节点值也要为“1”;一旦某个零部件i在变换过程中solx的值由“1”变为“0”,那么零部件i的所有后继节点的值要为“0”;
步骤4支配测试:对原个体和改进后的新个体进行一个支配测试,检查两个个体是否是支配的或者是非支配的.如果原个体支配新个体,新个体将被废除;如果新个体支配原个体,新个体将替换原个体;如果它们两个都是非支配,并且新个体都没有被外部存档所支配,新个体将被放到外部存档中,而原个体保持不变.
3.6更新参考集
参考集更新方法利用改进的新解不断地更新参考集,使参考集中始终保持高质量解和多样性解[14].
针对本文的3.3节,更新参考解集的过程如下:记sol∗为一个新解,算法将Ref中的b1个最好解按照目标函数值Z1从大到小进行排序.如果目标函数Z1(sol∗)大于Ref中的第b1个最好解,则淘汰当前Ref中的第b1个最好解,并根据目标函数值Z1(sol∗)将sol∗插入到合适的位置.将Ref中的b2个最好解按照目标函数值Z2从小到大进行排序,如果目标函数Z2(sol∗)小于Ref中的第b2个最好解,则淘汰当前Ref中的第b2个最好解,并根据目标函数值Z2(sol∗)将sol∗插入到合适的位置.如果这个新解sol∗在两个目标函数Z1(sol∗)和Z2(sol∗)中都是最优的,则保留sol∗在b1中位置,不和Ref中的b2个最好解进行比较.如果D(sol∗,Ref)值大于Ref中的第b3个最好解,则淘汰当前Ref中的第b3个最好解,并根据距离值D(sol∗,Ref)将sol∗插入到合适的位置.
4 算法的验证与分析
4.1算法的验证
为测试本文提出方法的有效性,实验中首先引用文献[9]中的一个案例进行验证,该实例包含25个零部件(不包括虚节点0),产品结构如图2所示,问题参数根据本文问题定义进行了修改如表4所示.
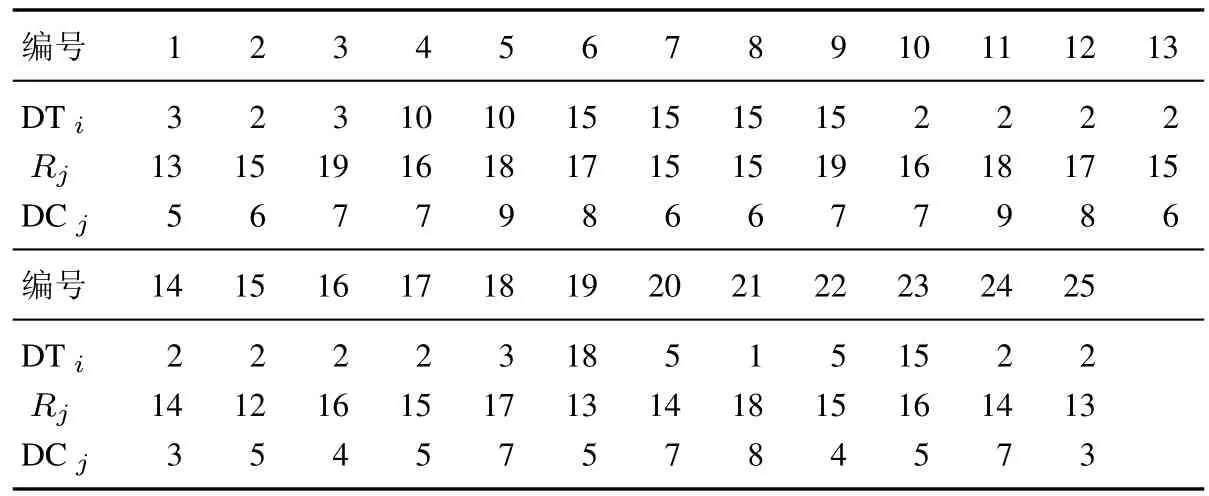
表4 问题参数Table 4 Problem parameters
算法应用JAVA语言编写,运行在使用Windows XP操作系统的Pentium IV(2.66GHz/2.0G)PC机上.零部件相互间的拆卸顺序依赖时间增量如图2所示,转换成本Cjk的取值在[1,10]范围内随机取值,转换时间ctjk在[1,10]范围内随机取值,转换资源rrjk在[1,10]范围内随机取值,总资源数Cr=200,表5所示为本算法迭代100次搜索到的Pareto解集.
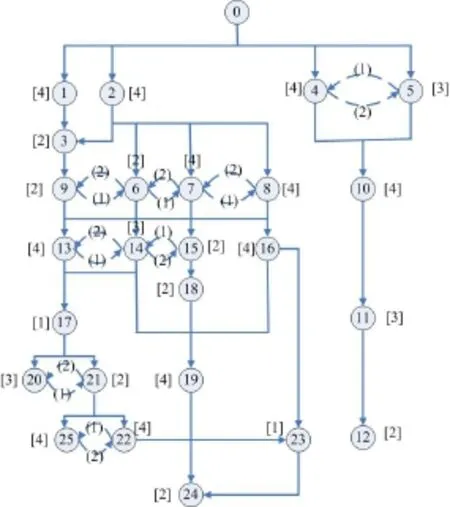
图2 产品结构图Fig.2 The diagram of product structure

表5 求解结果Table 5 Computational results
为了验证本文算法的有效性,和文献[15]中线性加权法进行对比验证.为了公平的比较,两种算法使用相同的编码方式、解码规则、重组算子以及解的改进过程.文献[15]解决的是在没有资源约束情况下完全拆卸序列多目标优化问题,所提方法为线性加权法把多目标问题转化为单目标优化问题进行求解,在测试过程中,根据本文问题对文献[15]算法进行修改,将本文中Z1,Z2两个优化目标转化为Z=w1Z1+w2Z2单目标进行试验(其中w1,w2为目标权重系数)与本文算法进行比较.两种算法参数设置为:最大迭代代数100,初始解种群P的大小为100,参考集规模b=20,对于文献[15]中的算法取b1=b2=10.对于本文算法取b1=b2=5,b3=10.文献[15]中的算法求解结果如表6所示.
通过对比表5与表6可以看出,本文搜索得到的六个Pareto解中拆卸时间最小为159 s,拆卸收益最大为5 475,说明本文所提算法在迭代次数相同可以得到较好的解.由于多目标分散搜索算法可在一次运算后求得若干Pareto解,求解效率较高,并且为决策者提供了较大的选择空间,从表5可以看出,若考虑拆卸收益最大,可选择方案1;若考虑拆卸时间最小,可选择方案3.

表6 分散搜索算法求解结果Table 6 Results of the scatter search algorithm
4.2与其它算法的对比
为了进一步测试本文算法的有效性,采用NSGA-II算法[16]和本文算法进行对比验证.实验中对文献[9]中的例子进行扩展,生成了7组不同的测试实例,相关参数均取整数形式,参数设置如表7所示,零部件数量分别为(50,80,100,150,200,250,300).资源种类数R=2,资源可用量C1=C2取值在[80,1 000]之间随机选取.

表7 不同的参数和取值范围Table 7 Different parameters and value range
本文SS算法参数设置如下:最大迭代代数100,初始解种群规模P=100,参考集规模b=35,b1= b2=10,b3=15.算法和NSGA-II算法采用相同的编码方式、解码规则.NSGA-II算法参数设置如下:最大迭代代数100,群体规模P=100,交叉概率为pc=0.6,变异概率为pm=0.005.选择算子采用轮盘赌方法,交叉算子采用3.4节中的PPX交叉.
本文SS算法和NSGA-II算法的结果评价标准如下[17].
1)间距评估S:用来测度所得Pareto前沿上相邻解间距离的变化情况.其定义为

2)最大散布范围评估D:用来测度目标空间中的两个极值解的距离.定义为

D的值越大,表明算法所获得的散布范围更广[17].
实验中采用3种评估标准对本文SS算法和NSGA-II算法进行评估,分别为Pareto解集中解的个数、间距评估和最大散布范围评估.为了评估SS算法和NSGA-II两种算法的性能,将7组不同的算例求解结果进行比较,实验中应用SS算法和NSGA-II算法对每个问题实例求解10次,统计每个实例的Pareto解集中平均解的个数Navg,平均解的间距Savg,平均解的最大散布范围Davg以及算法运行10次的平均运行时间(s),如表8所示.
图3和图4为SS算法和NSGA-II算法对算例1和算例3两个算例求解结果的比较图.由图3和图4可知,SS算法搜索到的解优于NSGA-II算法搜索到的解.图5为两种算法在七组算例中平均计算时间的比较图,由图5可知,SS算法的CPU运行时间比NSGA-II算法的少.
通过分析图3、图4、图5和表8中的实验数据,可以发现,1)在相同的参数下,随着问题规模的增大,相应的每个平均目标值也随着增大;2)算法对不同的问题规模进行求解会得到不同的近似有效解集,SS算法求解的结果优于NSGA-II算法;3)SS算法的CPU运行时间比NSGA-II算法的少;4)本文算法获得的Pareto解的数量多,间距小以及散布的范围广.由上可知,针对以上算例,本文算法求解结果比NSGA-II更加理想.

图3 50个零部件两种算法求解结果的比较图Fig.3 Comparison graph of two algorithms on 50 components
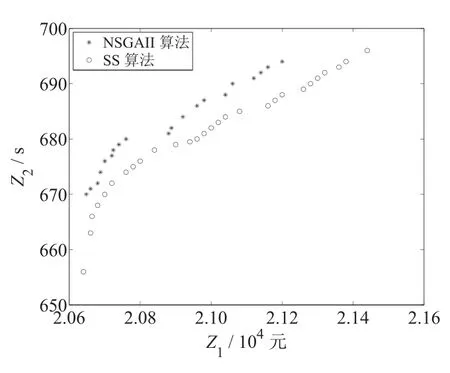
图4 100个零部件两种算法求解结果的比较图Fig.4 Comparison graph of two algorithms on 100 components

图5 两种算法计算时间的比较图Fig.5 Comparison graph of two algorithms on computing time

表8 两种算法在间距及最大散布范围上的比较Table 8 Comparison of the two algorithm on spacing and maximum spread on the range
5 结束语
本文针对MMSSDSOP建立了多目标整数规划模型.在分散搜索算法基本框架的基础上,开发了该问题的多目标SS算法.该算法产生了多样性好的初始解,并应用了参考集更新方法,子集产生方法,子集合并方法和解改进方法等来实现优化求解.对拆卸问题实例进行仿真分析,通过与NSGA-II算法进行比较,表明了提出的SS算法能够有效求解此模型,获得多目标拆卸序列优化问题的满意解.
[1]Wang H,Xiang D,Duan G H.A genetic algorithm for product disassembly sequence planning.Neurocomputing,2008,71(13):2720-2726.
[2]Lambert A J D.Exact methods in optimum disassembly sequence search for problems subject to sequence dependent costs.Omega:Journal of Internationnal Management Science,2006,34(6):538-549.
[3]Gonzáleza B,Adenso-Díazb B.A scatter search approach to the optimum disassembly sequence problem.Computers Operations Research,2006,33(6):1776-1793.
[4]Smith S S,Chen W H.Rule-based recursive selective disassembly sequence planning for green design.Advanced Engineering Informatics,2011,25(1):77-87.
[5]Kara S,Pomprasitpol P,Kebemick H.A selective disassembly methodology for end-of-life products.Assembly Automation,2005,25(2):124-134.
[6]Wang J F,Liu J H,Li S Q.Intelligent selective disassembly using the ant colony algorithm.Artificial Intelligence for Engineering Design Analysis and Manufacturing,2003,17(4):325-333.
[7]Chung C,Peng Q J.An integrated approach to selective disassembly sequence planning.Robotics and Computer Integrated Manufacturing,2005,21(4/5):475-485.
[8]Elsayed A,Kongar E,Gupta S M.An evolutionary algorithm for selective disassembly of end-of-life products.International Journal of Swarm Intelligence and Evolutionary Computation,2012,22(1):1-7.
[9]Kalayci C B,Gupta S M.Ant colony optimization for sequence-dependent disassembly line balancing problem.Journal of Manufacturing Technology Management,2013,24(3):413-427.
[10]Marti R,Laguna M,Glover F.Principles of scatter search.European Journal of Operational Research,2006,169(2):359-372.
[11]谭园园,魏震,王森等.基于VRPTW-AT模型的钢包优化调度方法.系统工程学报,2013,28(1):94-100. Tan Y Y,Wei Z,Wang S,et al.Optimization algorithm for ladle scheduling based on the VRPTW-AT.Journal of Systems Engineering,2013,28(1):94-100.(in Chinese)
[12]NebroAJ,LunaF.AbYSS:Adaptingscattersearchtomultiobjectiveoptimization.IEEETransactionsonEvolutionaryComputation,2008,12(4):439-457.
[13]Bierwirth C,Mattfeld D C.Production scheduling and rescheduling with genetic algorithms.Evolutionary Computation,1999,7(1):1-18.
[14]Adenso-Díaz B,Garcia-carbajal S,Lozano S.An empirical investigation on parallelization strategies for scatter search.European Journal of Operational Research,2006,2(1):490-507.
[15]郭希旺,刘士新,王大志.多目标拆卸序列优化问题的分散搜索算法.东北大学学报(自然科学版),2012,3(11):56-59. Guo X W,Liu S X,Wang D Z.Scatter search for solving multi-objective disassembly sequence optimization problems.Journal of Northeastern University(Natural Science Edition),2012,3(11):56-59.(in Chinese)
[16]Kalyanmoy D.A fast and elitist multiobjective genetic algorithm:NSGA-II.IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[17]张勇德,黄莎白.多目标优化问题的蚁群算法研究.控制与决策,2005,20(2):170-176. Zhang Y D,Huang S B.On ant colony algorithm for solving multiobjective optimization problems.Control and Decision,2005,20(2):170-176.(in Chinese)
Scatter search algorithm for multi-objective selective disassembly sequence optimization problems
Guo Xiwang,Liu Shixin,Wang Dazhi
(School of Information Science Engineering,Northeastern University,Shenyang 110819,China)
Selective disassembly sequence optimization problem with multi-resource constraints and sequencedependence is considered by establishing a multi-objective model with the objective of maximizing profit and minimizing disassembly time.A multi-objective scatter search(SS)method is put forward to solve this problem.Based on the characteristics of the problem,an initial solution diversification generation method is put forward which satisfies the crossover combination operator,which maintains the disassembly precedence relationship,and improved reference set updating strategy.In order to further improve the quality of the solution,a local search strategy is designed and external archive method is employed to store Pareto solution set.The results of SS and other algorithms in solving several computational experiments are compared,and the experimental results demonstrate the validity of the model and SS algorithm.
selective disassembly sequence optimization;multi-resource constraints;multi-objective;scatter search algorithm
TP18
A
1000-5781(2016)03-0307-10
10.13383/j.cnki.jse.2016.03.003
郭希旺(1981-),男,辽宁营口人,博士生.研究方向:绿色制造,组合优化.Email:x.w.guo@163.com;
刘士新(1968-),男,辽宁调兵山人,教授,博士生导师.研究方向:生产计划与调度,物流系统建模与优化,组合优化算法. Email:sxliu@mail.neu.edu.cn;
王大志(1978-),男,辽宁沈阳人,讲师,研究方向:智能优化算法.Email:wangdazhi1@ise.neu.edu.cn.
2013-08-23;
2014-09-11.
国家自然科学基金资助项目(71171038);中央高校基本科研业务费资助项目(N110404024).

