基于逻辑回归模型的化探异常信息识别研究——以克拉玛依地区为例

周曙光，周可法，崔遥，王金林，汪玮，丁建丽

(1.中国科学院新疆生态与地理研究所，新疆矿产资源研究中心，新疆 乌鲁木齐　830011；2.新疆大学资源与环境科学学院，新疆 乌鲁木齐　830046；3.中国科学院大学，北京　100049)



基于逻辑回归模型的化探异常信息识别研究
——以克拉玛依地区为例

周曙光1,2,3，周可法1，崔遥1，王金林1，汪玮1，丁建丽2

(1.中国科学院新疆生态与地理研究所，新疆矿产资源研究中心，新疆 乌鲁木齐830011；2.新疆大学资源与环境科学学院，新疆 乌鲁木齐830046；3.中国科学院大学，北京100049)

化探数据对矿产资源勘查工作有着重要作用，其中比较关键的工作就是从化探数据中识别矿床相关的化探异常信息。在化探异常信息识别工作中也发展出了较多的技术，但是它们大多针对单变量进行分析。为了对多变量化探数据进行分析并识别金矿相关的地球化学异常信息，笔者将逻辑回归模型用于研究区化探数据分析，通过研究区内对金矿预测比较有价值的16种元素的逻辑回归建模及模型应用，发现逻辑回归是一种有效的化探多变量数据分析和建模技术，研究结果显示，笔者建立的逻辑回归模型不仅可以有效识别已知金矿区的地球化学异常信息，而且对那些还未发现矿床的区域具有预测作用，能够为矿产资源勘查工作重点区域的选择提供指导。

逻辑回归；地球化学异常；金矿

化探数据在成矿预测工作中起着积极和重要的作用，往往能够提供非常有价值和明确的指导(杨万志等，2013)。有研究在运用地物化遥和矿床数据进行钼多金属成矿预测工作中发现，在选择的7个找矿标志中，地球化学的权重最高，代表地球化学标志是致矿的最重要要素(肖巧艳等，2011)。王学求等利用区域化探扫面数据在全国范围内圈定了11处金地球化学块体，发现中国金地球化学块体与金矿床的空间对应关系十分密切(王学求，2013)。地球化学块体理论研究发现，有矿集区存在就一定有地球化学块体存在(王少怀，2011；王学求等，2007，2013)。

化探异常信息的识别是化探数据研究中的关键问题之一，有大量研究(AFZAL, 2013; CHENG, 2012; CHENG et al., 1994; ZUO et al., 2009; 蒋友欣等，2007; 金俊杰等，2011; 雷恩等，2012; 李宝强等，2004; 李宾等，2012; 师淑娟等，2011; 汪等等，2013)都能说明。因此，也发展出了很多化探异常信息识别技术，然而各种方法的理论基础不一，它们也都有各自的优势和局限，其中较为普遍的局限性是无法直接进行多变量分析。

Logistic regression(逻辑回归)模型是一种常用的机器学习算法，该算法在商业和服务行业(彭凯等，2011)、城市发展(姜文亮等，2008)、医疗(SILKE et al., 2010; YASUDA et al., 2009)、地质矿产(MOKHTARI, 2014)等很多领域都有应用，尤其是在滑坡监测研究(谭龙等，2014; 夏添等，2013; 许冲等，2013)中，逻辑回归模型通常都能够得到很好的结果。然而，逻辑回归模型在化探数据分析方面的应用研究鲜有报道。笔者将对此进行探讨，以期为化探数据分析和成矿预测工作提供技术支持。

1　区域地质及矿床地质概况

研究区(图1)主要受北北东向断裂控制，区内自北向南依次分布着哈图、安齐、达拉布特和一家人等规模较大的断裂。达拉布特蛇绿混杂岩带沿达拉布特大断裂呈带状展布，面积约为50km2，受到逆冲断裂为主的叠瓦状构造破坏，洋壳物质常以残片形式赋存于古大陆边缘的陆源碎屑物中，显示残留性地幔源的地球化学特征(张弛等，1992)。本地区代表性岩体包括庙儿沟岩体、哈图西岩体、阿克巴斯套岩体和克拉玛依北岩体，锆石的LA-ICP-MS U-Pb定年结果表明它们的年龄为300 Ma (苏玉平等，2006)。

1.克拉玛依；2.哈图断裂；3.达拉布特断裂；4.断裂；5.蚀变带；6.太勒古拉组；7.金矿床(点)；8.安齐断裂；9.一家人断裂；10.花岗岩体；11.包古图组；12.西贝库拉组图1　研究区构造、地层、岩浆岩和蚀变区分布简图Fig.1　Simplified map of regional tectonics, magmatic rocks, and alteration

2　数据及预处理

笔者主要以克拉玛依幅1∶20万化探扫面数据(空间分辨率约为2km)和该区的矢量基础地质，以及矿产资料为依据进行分析。其中，化探数据集中包括对金铜矿成矿预测工作比较有指示意义的热液或低温热活动相关的元素(表1)。从表1可以看出，这些元素的标准差较大，说明不同采样位置处的元素含量变化很大，区内元素分布很不均匀。区内某元素最高含量通常是其最低含量的数十倍甚至上千倍。这些元素大多呈正偏态分布，而且通常都有一个尖峰。

表1　元素的基本统计信息表

为了便于运算和结果展示，首先需要将点状分布的数据通过空间插值方法转换成栅格数据，这一过程可以借助ArcGIS的空间插值工具完成。笔者使用Kring插值算法对表1中的各种元素进行插值并将插值结果保存成空间分辨率约为2km(与原始化探样点间隔相同)的栅格数据。

3　逻辑回归模型及其应用

3.1逻辑回归模型简介

逻辑回归可以根据单个或多个自变量对二分类或多分类的因变量进行分类和预测，逻辑回归得到的结果通常表示因变量处于某种特定状态时的概率大小。经典的多元线性回归模型通常被表示成：

(1)

而逻辑回归模型则常被表示成：

(2)

由此可见，式1与式2非常相似，不同的是式2通常用来对分类变量进行拟合，而且从本质上讲，式2拟合的是发生的概率。

然而，逻辑回归模型在实际应用中存在两点局限。首先，模型的左侧和右侧的取值区间不一致，左侧的取值范围为[0,1]，而右侧的取值范围为整个实数空间；其次是因变量和自变量在很多时候都不呈直线关系，而是呈S型曲线关系。为了解决这一问题，Logit变换被引入逻辑回归模型，因此逻辑回归模型就变形为(张文彤等，2004)：

Logit(P)=α+β1x1+β2x2+…+βnxn

(3)

或

(4)

或

(5)

其中，α为模型的常数项，βi(i=1,2,…,n)为回归系数，表示自变量xi(i=1,2,…,n)改变一个单位时Logit(P)的平均改变量。

以艾略特波浪理论分析国证A指走势。2008年1月结束第（3）浪，其后的第（4）浪是一个大型水平三角形。其中，2008年1月至11月的急跌为（4）浪A，2008年11月至2010年11月为（4）浪 B，2010年 11月至2012年12月为（4）浪C，2012年12月至2013年10月为（4）浪D，2013年10月至2014年5月为（4）浪E最后一跌。（4）浪E规模很小，有时会出现此等情况，分析师容易被迷惑。

3.2逻辑回归模型建立

逻辑回归模型能够根据各输入自变量对因变量的贡献大小决定最终模型中将纳入哪些自变量，即对因变量影响较大的自变量进入模型，对因变量贡献小的自变量则被放弃。在建立逻辑回归模型之前，首先需要选择训练样本。笔者的研究目的是建立一个化探异常信息识别模型，使其能够用于成矿预测工作。因此，首先根据以下原则确定训练样本：

(1)根据研究区的地质资料，将区内所有或者部分已知金矿床(点)附近的化探样本作为有矿地区的训练样本，同时要求这些训练样本位于构造较发育地区或者处于地层的接触带附近。

(2)根据研究区的地质资料，在无已知金矿床(点)、构造不发育且距地层接触带较远的地区选择一定量的样本，作为无矿地区的化探数据训练样本。

根据以上原则，笔者共选择48个有矿地区的化探训练样本，同时选择50个无矿地区的化探训练样本。训练样本位置见图2。

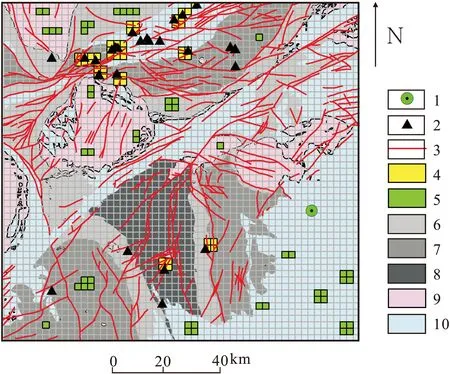
1.克拉玛依市；2.已知金矿；3.断裂带；4.有矿训练样本；5.无矿训练样本；6.包古图组；7.太勒古拉组；8.西贝库拉组；9.花岗岩体；10.第四系沉积图2　有矿和无矿训练样本分布图Fig.2　The distribution of training samples

笔者基于SPSS 19.0建立逻辑回归模型，自变量进入方程的方式为Forward wald方法。最终构建的模型为：

Logit(P)=-49.401-0.185×Ag+

99.655×Bi+1.543×Cu-1.142×Pb

(6)

模型的训练结果见表2，可见模型具有较好的效果。

将训练得到的逻辑回归模型用于整个研究区的化探数据分析，结果见图3。图中的分类方法为natural breaks (Jenks)。通过对结果的分析发现，红色区域占整个研究区的10.63%，研究区内已知金矿床(点)共有27个，其中17个位于红色区域内，占所有已知金矿床(点)的62.96%。红色和黄色区域占研究区总面积的39.18%，几乎所有已知金矿床(点)都位于该区域内(只有研究区最南部的矿点紧贴该区域边缘)。结合图2和图3可以发现，图3中R1区域都有已知金矿床(点)分布，即使这些区域的化探数据没有被用于建模过程，在最终的预测结果中，R1区域均显示为强或中等化探异常区。另外，R2区域也显示为规模较大的强异常区，并且R2区域的构造较发育，或者位于不同地质体的接触带附近，但是R2区域还没有发现已知矿床。

表2　逻辑回归模型训练结果表

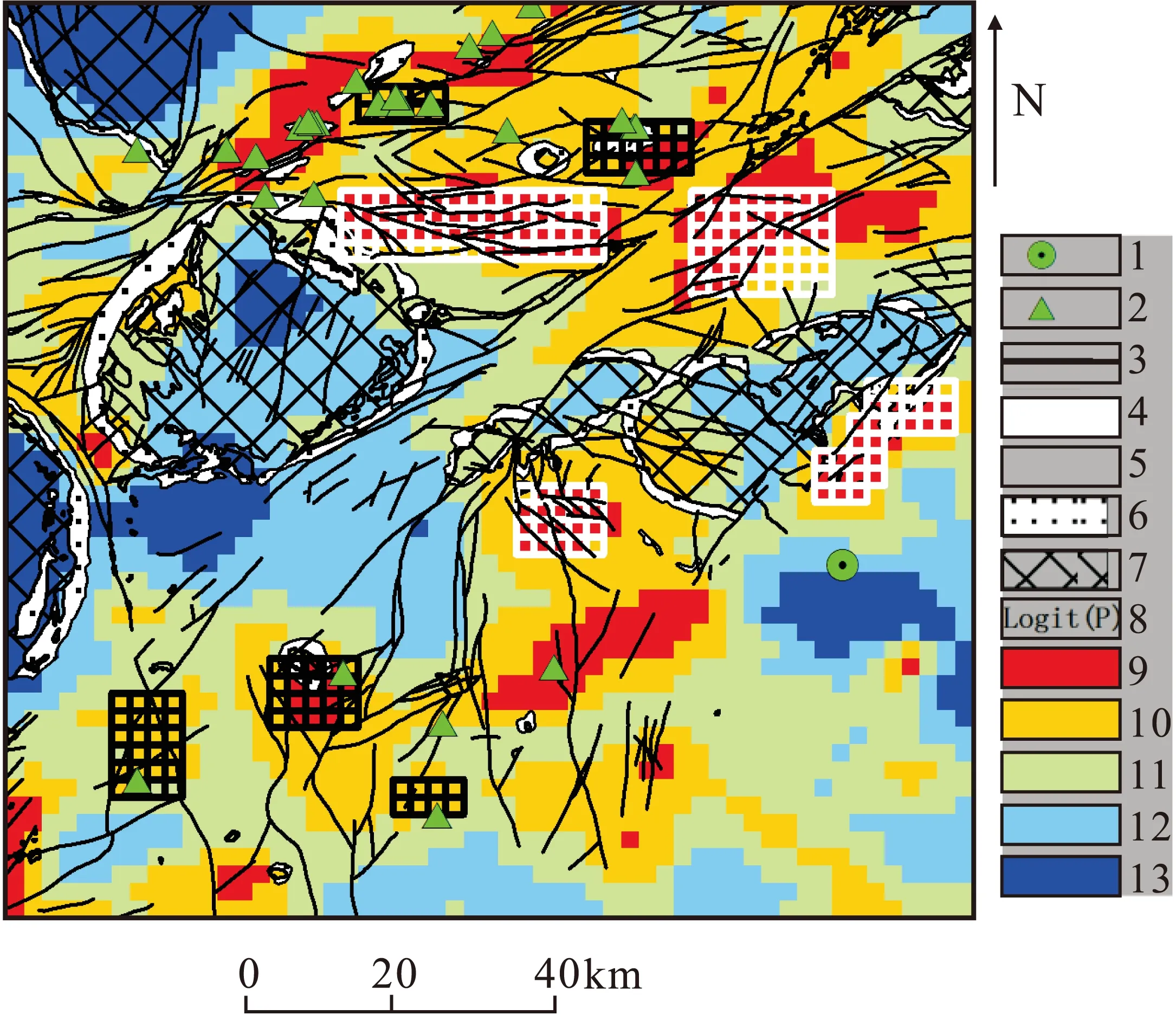
1.克拉玛依市；2.已知金矿；3.断裂带；4.R1；5.R2；6.蚀变带；7.花岗岩体；8. Logit(p)；9. 10.92～45.98；10. 1.23～10.91；11. -7.43～1.22；12. -17.62--7.44；13. -36.52～-17.63图3　逻辑回归模型应用效果图Fig.3　The application result of logistic regression

4　结论

结合地理信息系统软件ArcGIS和统计软件SPSS，可以比较容易地对化探数据进行逻辑回归建模，而且获得的逻辑回归模型具有较好的应用效果，能够比较准确地识别已知金矿床(点)所在区域的化探异常信息。

逻辑回归应用结果显示，研究区内某些区域显示为规模较大的强异常区，并且这些区域具有构造比较发育，或者位于不同地质体接触带附近的特点，但是这些区域还没有发现已知矿床，建议将这些区域作为今后勘查工作的重点区域。

逻辑回归建模时需要确定训练样本，因此，在具有基础地质资料和一定量的已知矿床(点)，并且进行了化探工作的区域能够使用逻辑回归模型进行化探异常信息识别和成矿预测工作。

姜文亮, 张晓通,李霖, 等. 基于GIS和空间逻辑回归模型的城市空间扩展预测——以深圳市龙岗区为例[J]. 测绘科学, 2008, 33(4): 172-174.

JIANG Wenliang, ZHANG Xiaotong, LI Lin, et al. Urban spatial expansion forecast based on GIS & spatial logistic regression model [J]. Science of Surveying and Mapping, 2008, 33(4): 172-174.

蒋友欣, 黄厚辉. 基于人工免疫理论的化探数据降噪方法[J]. 新疆地质, 2007, 25(1): 119-121.

JIANG Youxin, HUANG Houhui. The way of de-noising geological anomaly data based on artificial immunity information combination [J]. Xinjiang Geology, 2007, 25(1): 119-121.

金俊杰, 陈建国. 地球化学异常提取的自适应衬值滤波法[J]. 物探与化探, 2011, 35(4): 526-531.

JIN Junjie, CHEN Jianguo. A self-adaptive method of contrast filtering for extracting geochemical anomaly [J]. Geophysical & Geochemical Exploration, 2011, 35(4): 526-531.

雷恩, 王丹, 杨洪永, 等. 重庆东北城口地区黑色岩系地球化学异常模式[J]. 地质科技情报, 2012, 31(2): 35-39.

LEI En, WANG Dan, YANG Hongyong, et al. A Geochemical Anomaly Model for Black Shales in Chengkou Region of Northest Chongqing [J]. Geological Science and Technology Information, 2012, 31(2): 35-39.

李宝强, 孙泽坤. 区域地球化学异常信息提取方法研讨[J].西北地质, 2004, 37(1): 102-108.

LI Baoqiang, SUN Zekun. Study on the method of geochemical anomalies analysis [J]. Northwestern Geology, 2004, 37(1): 102-108.

李宾, 李随民, 韩腾飞, 等. 趋势面方法圈定龙关地区化探异常及应用效果评价[J]. 物探与化探, 2012, 36(2): 202-207.

LI Bin, LI Suimin, HAN Tengfei, et al. The application of trend surface analysis to delineating geochemical anomalies in Longguan area and its effect [J]. Geophysical & Geochemical Exploration, 2012, 36(2): 202-207.

彭凯, 秦永彬, 许道云. 基于逻辑回归的客户稳定度建模[J]. 计算机工程, 2011, 37(9): 12-15.

PENG Kai, QIN Yongbin, XU Daoyun. Customer Stability Modeling Based on Logistic Regression [J]. Computer Engineering, 2011, 37(9): 12-15.

师淑娟, 王学求, 宫进忠. 金的地球化学异常与金矿床规模之间关系的统计学特征-以河北省为例[J]. 中国地质, 2011, 38(6): 1562-1567.

SHI Shujuan, WAN Xueqiu, GONG Jinzhong. Statistic relationship between geochemical anomalous areas and gold reserves: a case study of Hebei Province [J]. Geology in China, 2011, 38(6): 1562-1567.

苏玉平, 唐红峰, 侯广顺, 等. 新疆西准噶尔达拉布特构造带铝质A型花岗岩的地球化学研究[J]. 地球化学, 2006, 35(1): 55-67.

SU Yuping, TANG Hongfeng, HOU Guangshun, et al. Geochemistry of aluminous A-type granites along Darabut tectonic belt in west Junggar, Xinjiang [J]. Geochimica, 2006, 35(1): 55-67.

谭龙, 陈冠, 王思源, 等. 逻辑回归与支持向量机模型在滑坡敏感性评价中的应用[J]. 工程地质学报, 2014, 22(1): 56-63.

TAN Long, CHEN Guan, WANG Siyuan, et al. Landslide susceptibility mapping based on logistic regression and support vector machine [J] . Journal of Engineering Geology, 2014, 22(1): 56-63.

汪等, 李佑国, 赵伟,等. 异常下限衬值滤波法在然乌幅化探数据处理中的应用[J]. 物探与化探,2013, 37(2): 344-349.

WANG Deng, LI Youguo, ZHAO Wei, et al. The Application of the anomaly threshold contrast filtering method to the geochemical data processing of the Ranwu sheet [J]. Geophysical & Geochemical Exploration, 2013, 37(2): 344-349.

王少怀. 紫金山矿集区地球化学异常特征及找矿潜力预测[J]. 大地构造与成矿学, 2011, 35(1): 156-160.

WANG Shaohuai. Characteristics of Gold Geochemical Anomalies and Ore Potential Forecasting of the Zijinshan Area of Extensive Gold Mineralizatio [J]. Geotectonica et Metallogenia, 2011, 35(1): 156-160.

王学求. 勘查地球化学近十年进展[J]. 矿物岩石地球化学通报, 2013, 32(2): 190-197.

WANG Xueqiu. A Decade of Exploration Geochemistry [J]. Bulletin of Mineralogy, Petrology and Geochemistry, 2013, 32(2): 190-197.

王学求, 申伍军, 张必敏, 等. 地球化学块体与大型矿集区的关系-以东天山为例[J]. 地学前缘, 2007, 14(5): 116-123.

WANG Xueqiu, SHEN Wujun, ZHANG Bimin, et al. Relationship of geochemical blocks and ore districts: examples from Eastern Tianshan metallogenic belt, Xinjiang, China[J]. Earth Science Frontiers,2007, 14(5): 116-123.

夏添, 常鸣. 改进逻辑回归方法在滑坡敏感性评价中的应用研究[J]. 物探化探计算技术, 2013,35(2): 185-188.

XIA Tian, CHANG Ming. Improving autologistic regression method in the research on the application of landslide sensitivity evalution [J]. Computer Techniques for Geophysical and Geochemical Exploration, 2013, 35(2): 185-188.

肖飞. 新疆哈图金矿容矿构造特征及勘探方向[J]. 新疆工学院学报, 1999, 20(4): 271-273.

XIAO Fei. Characteristics of structure and direction of prospecting in Xinjiang Hatu gold ore [J]. Journal of Xinjiang Institute of Technology, 1999, 20(4): 271-273.

肖巧艳, 王功文, 张寿庭, 等. 豫西南杜关-云阳钼多金属成矿预测研究[J]. 现代地质, 2011, 25(1):94-100.

XIAO Qiaoyan, WANG Gongwen, ZHANG Shouting, et al. Research on M olybdenum Polym etallicM etallogenic Prognosis in Duguan-Yunyang D istrict, Southwest H enan Province [J]. Geoscience, 2011, 25(1): 94-100.

许冲, 戴福初, 徐素宁, 等. 基于逻辑回归模型的汶川地震滑坡危险性评价与检验[J]. 水文地质工程地质, 2013, 40(3): 98-104.

XU Chong, DAI Fuchu, XU Suning, et al. Application of logistic regression model on the Wenchuan earthquake triggered landslide hazard mapping and its validation [J]. Hydrogeology & Engineering Geology, 2013, 40(3): 98-104.

杨万志, 周军, 庄道泽, 等. 新疆西昆仑-阿尔金成矿带区域地球化学勘查进展[J]. 西北地质,2013,46(1): 110-118.

YANG Wanzhi, ZHOU Jun, ZHUANG Daoze, et al. A Progress of Region Geochemical Exploration of Metallogenic Belt from West Kunlun Altun Ranges in Xinjiang [J]. Northwestern Geology, 2013, 46(1): 110-118.

张弛, 黄萱. 新疆西准噶尔蛇绿岩形成时代和环境的探讨[J]. 地质论评, 1992, 38(6): 509-524.

ZHANG Chi, HUANG Xuan. The ages and tectonic settings of ophiolites in west Junggar, Xinjiang [J]. Geology Review, 1992, 38(6): 509-524.

张凤军. 哈图金矿金的伴生矿物与金矿脉地质特征的探讨[J]. 新疆有色金属, 2003, 26(3): 5-9.

ZHANG Fengjun. The study of geological characteristics of the gold associated minerals and gold vine of Hatu gold deposit [J]. Journal of Xinjiang Nonferrous Metals, 2003, 26(3): 5-9.

张文彤, 董伟. SPSS统计分析高级教程[M].北京：高等教育出版社, 2004.

ZHANG Wentong, DONG Wei. Advanced statistics analysis in SPSS [M]. Beijing: Higher Education Press, 2004.

朱永峰, 安芳, 徐存元,等. 新疆哈图及其周边金铜成矿规律和深部找矿预测[M]. 北京:地质出版社, 2013.ZHU Yongfeng, AN Fang, XU Cunyuan, et al. Xinjiang Hatu jiqi zhoubian jintong chengkuang guilhe zhaokuang yuce [M]. Beijing: Geology Publishing House, 2013.

AFZAL S.H.P.Application of concentration-number (C-N) multifractal modeling for geochemical anomaly separation in Haftcheshmeh porphyry system [J].NW Iran. Arabian Journal of Geosciences , 2013,6:957-970.

CHENG Q M. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas [J]. Journal of Geochemical Exploration , 2012, 122:55-70.

CHENG Q M, AGTERBERG F.P., BALLANTYNE S.B..The separation of geochemical anomalies from background by fractal methods [J]. Journal of Geochemical Exploration, 1994, 51:109-130.

MOKHTARI A.R.. Hydrothermal alteration mapping through multivariate logistic regression analysis of lithogeochemical data [J]. Journal of Geochemical Exploration, 2014, 145:207-212.

SILKE B., KELLETT J., ROONEY T., et al. An improved medical admissions risk system using multivariable fractional polynomial logistic regression modelling [J]. Qjm-an International Journal of Medicine, 2010, 103:23-32.

YASUDA H., YOSHIDA K., SEGAWA M., et al. Metallomics study using hair mineral analysis and multiple logistic regression analysis: relationship between cancer and minerals [J]. Environmental Health and Preventive Medicine, 2009, 14:261-266.

ZUO R G, CHENG Q M, AGTERBERG F.P., et al. Application of singularity mapping technique to identify local anomalies using stream sediment geochemical data, a case study from Gangdese, Tibet, western China [J]. Journal of Geochemical Exploration, 2009，101：225-235.

Application of Logistic Regression Methods in Geochemical Data Analysis and Mineral Exploration: Example from Karamay Region

ZHOU Shuguang1,2,3, ZHOU Kefa1, CUI Yao1, WANG Jinlin1, WANG Wei1, DING Jianli2

(1.Xinjiang Research Center for Mineral Resources, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, Xinjiang, China; 2.Xinjiang University, Urumqi 830046, Xinjiang, China; 3.University of Chinese Academy of Sciences, Beijing 100049, China)

Geochemical data is essential for mineral exploration, and one of the main challenges is how to identify the anomaly that was related to the formation or locations of mineral deposits. Many techniques have been developed to identify geochemical anomalies in the past years, but most of these techniques are designed for univariate data. To identify geochemical anomalies from multivariate geochemical data and to get gold deposits related information, logistic regression method is used to analyze geochemical data (sixteen hydrothermal/epithermal elements are included) of this study area. The results demonstrate that the developed logistic regression model is effective for geochemical anomalies identification and gold prediction, because the model can not only identify the geochemical anomalies where there are known gold deposits, but also identify other strong geochemical anomalies where there is no known deposit. Therefore, the logistic regression method is recommended to be used to geochemical anomalies identification and mineral prediction.

logistic regression; geochemical anomaly; gold deposit

2015-02-03；

2015-05-13

国家自然科学基金(U1129302)、科技支撑计划项目(2012BAH27B05-06)

周曙光(1985-)，男，河南驻马店人，中科院新疆生态与地理研究所矿产资源研究中心在读博士，主要从事数据挖掘和成矿预测相关研究工作。E-mail：zhoushuguang1010@163.com

P431

A

1009-6248(2016)01-0234-07