基于单目离面视觉的结构振动检测

喻其炳　尹爱军　薛　磊　张　泉

1.重庆工商大学装备系统服役健康保障国际联合研究中心, 重庆，4000672.重庆大学机械传动国家重点实验室，重庆，400044



基于单目离面视觉的结构振动检测

喻其炳1尹爱军2薛磊2张泉2

1.重庆工商大学装备系统服役健康保障国际联合研究中心, 重庆，4000672.重庆大学机械传动国家重点实验室，重庆，400044

针对常规视觉测量中光学系统复杂、计算量大等问题，提出了一种离面视觉测量方法。讨论了离面振动成像的基本原理，结合模态分析理论，研究了常规成像条件下单相机结构振动特征参数的识别及无激励振型分析。悬臂梁的离面视觉振动测试实验、传统传感器测量实验及ANSYS仿真的对比结果表明，所提出方法可以准确识别低阶固有频率、阻尼和振型等模态信息。最后分析了该方法的后续研究方向。

离面视觉；视觉测量；振动参数识别；振型

0　引言

结构振动参数识别及振型检测是结构振动分析的重要内容。传统振动分析方法一般采用单个或多个振动传感器提取结构振动信息[1]，检测系统复杂，空间分辨率低,且在一定程度上可能会改变结构的原有动力学特性。视觉测量是一种非接触式振动测量方法，它具有全场测量、不改变被测物的振动特性等优点，在微电子器件自动检测、工业产品质量在线监控以及结构三维形状测量等方面已得到广泛应用[2]。

视觉测量方法中，基于结构光、单摄像机以及多目立体视觉的测量方法已得到广泛的研究和应用[3-9]。Jing等[5]利用结构光测量系统，对复杂三维轮廓进行了高精度的尺寸测量并进行了像素级的结构三维轮廓重建。Teyssieux等[6]利用单个高速CCD相机和显微成像系统，实现了MEMS悬臂梁的面内运动位移和高频振动的精确测量。Wang等[7]通过两个高清晰度、高频相机得到结构三维振动散斑图像，利用数字图像相关法实现了结构的全场振动模态、应变等测量。Seungbae等[8]利用高速相机获取PCB电路板的离面振动图像，得到电路板的振动模态信息以及振动幅值随时间变化的分布图。

上述结构振动视觉分析方法，有些需要额外的结构光投射系统；有些需要复杂昂贵的光路系统与高速高精度成像系统；有些则需要进行大量的匹配运算等。本文针对这些问题，提出一种常规成像条件下的离面视觉测量方法，该方法利用单个相机获取结构离面振动信息，结合实验模态分析理论，识别结构振动特征参数和振型。最后进行了悬臂梁冲击响应实验。与ANSYS有限元分析的对比结果表明，所提出方法能够准确有效地实现结构振动分析。

1　离面视觉测量原理

1.1离面振动成像原理

根据针孔成像模型[10-12]，给出离面视觉振动检测原理，如图1所示。相机垂直振动方向成像，离面位移造成物距大小的改变，使得成像大小及位置发生改变，通过分析这种成像变化即可获得结构振动特性。

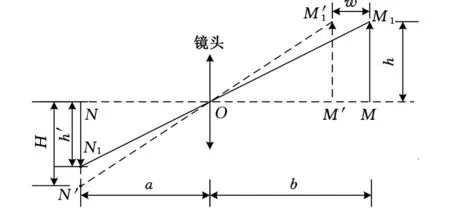
图1　摄像机成像等效针孔模型

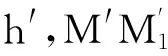
(1)

由式(1)可知，随着物距的增加，离面位移引起的测量变量会显著减小。在本文的实际测量中，物距b一般远大于振动位移w，故式(1)可以近似简化为

(2)

此时，离面位移量与相机成像的像素位移大小之间成近似的线性关系。

1.2振动信息提取

边缘特征检测法是一般图像处理问题的关键[13]。一般情况下，边缘信息在图像上呈现出不连续性，如灰度突变、亮度变化等。经典的图像边缘检测方法有Roberts算子、Sobel算子、Laplace算子以及Canny算子等，这些方法主要是使用图像梯度的极大值或一阶、二阶导数来检测图像边缘，通过微分算子模板和图像进行卷积来完成。Canny算子在噪声抑制和边缘检测之间取得较好的平衡，具有很好的边缘检测性能。

如图2a所示，在被测结构上设置具有反差颜色的线状边缘标志，经过图像滤波和Canny边缘提取算法处理得到包含边缘位置信息的图像(图2b)。由图2可知，相邻两帧图像中的边缘位置分别为H1和H2，通过计算每幅图像中边缘线位置的差值ΔH=H1-H2，即可得到线状边缘标志物的运动信息，并根据式(2)获得此时结构的振动信息。

(a)　　　　　　　　　　　(b)图2　边缘提取示意图

1.3模态参数识别方法

在模态分析中，通常将系统离散化为N个自由度的模型进行分析[14]。设X=(x1,x2,…,xN)T和F=(F1,F2,…,FN)T分别为系统各点的位移响应向量和激振力向量，X(ω)和F(ω)分别为位移响应与激振力的傅里叶变换，有

X(ω)=H(ω)F(ω)

(3)

即

其中，H(ω)称为频响函数矩阵，是一个对称阵。

在理想脉冲激励下，系统的输入为F(ω)=[F1F2…FN]T，特别地，当在p点进行单点激励时，有F(ω)= [0…0Fp0…0]T，则由式(3)得系统第r阶脉冲响应为

(4)

其中，rHij(ω)为该点第r阶模态对频响函数的贡献，rX(ω)=[rx1j(ω)rx2j(ω)…rxNj(ω)]T，

rxij(ω)为该点第r阶频域脉冲响应函数。由式(4)可以看出，在理想脉冲激励下，由系统脉冲响应rX(ω)得到的模态参数与由系统传递函数rH(ω)得到的模态参数之间相差一个常数。

由模态分析理论知[1]，系统归一化的第r阶模态振型向量为

(5)

式中，rRij为系统中对应点的第r阶留数值。

本文采用的归一化方法为：以模态振型向量中最大元素取值为1，rRsj为留数向量中的最大值。

当系统各阶模态较为分散时，在实模态条件下，由单模态识别法得系统中各点的第r阶留数值为

rRij=-2σrImrHij(ωr)

(6)

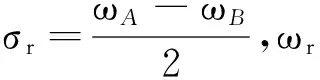
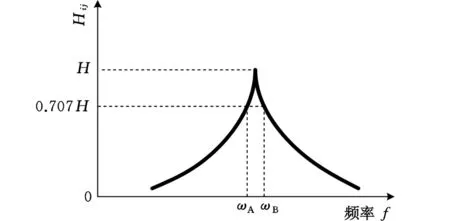
图3　单模态识别法的幅频曲线图

系统的第r阶阻尼比为

(7)

模态振型实质上是指结构上各测点之间的相对位移关系，是一组比值，非绝对量[15]。结合式(4)～式(6)可知，由系统脉冲响应rX(ω)得到的模态振型与由系统传递函数rH(ω)得到的模态振型在进行归一化之后是相同的。

2　实验设计及数据分析

2.1实验系统

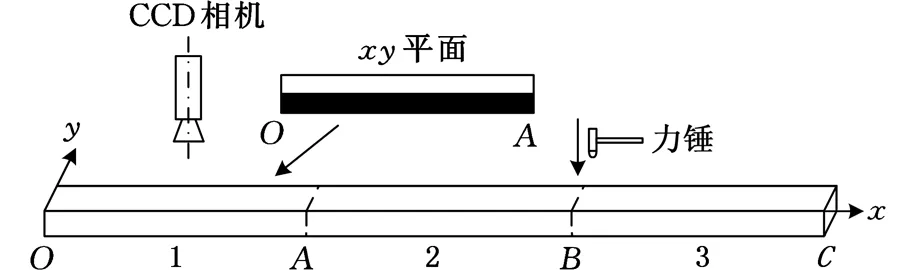
(a)实验示意图

(b)实验装置图图4　实验系统

实验系统如图4所示，其中相机为德国Baumer公司的TXG03cCCD相机，最高分辨率为656pixel×490pixel，最高分辨率下的最高帧率为90帧/s。本研究分别采用150帧/s(200pixel×200pixel分辨率)和60帧/s两种帧率模式进行实验。实验中，由于是离面测量，相机应正对xy面放置，相机中心轴与z轴平行。由于相机越靠近固定端，测得的像素位移越小，为了保证一定的分析精度，本实验悬臂梁振动检测点为A点。此外，为了后续数据分析的方便，将悬臂梁A点分析区域固定在相机视场内，实验中相机与悬臂梁之间的距离为35cm。选取拾振点时要尽量避免拾振点在模态振型的节点上，该实验取拾振点为B敲击点处。悬臂梁为长(x向)550mm、宽(y向)30mm、高(z向)3mm的合金铝板，其密度为2900kg/m3，弹性模量为63GPa。在悬臂梁xy面中间，为黑白交界的特征线。

实验中采用的激励装置为橡胶帽脉冲力锤，其频率特性如图5所示，力锤频谱在截止频率fc=75Hz以内是平稳的[1]。

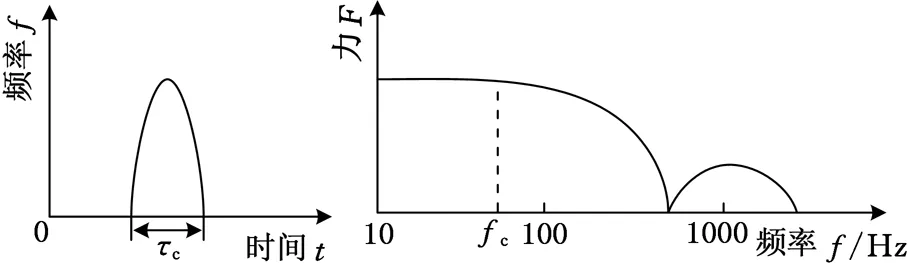
(a)锤击产生的　 　　(b)锤击冲击力频谱图　　冲击力时域图图5　脉冲力锤频率特性

2.2数据分析

2.2.1振动频率测量

图6a为140pixel×140pixel分辨率下，帧率为150帧/s时，在B点进行锤击激励，悬臂梁A点的冲击响应时域波形；根据傅里叶变换得其频率响应曲线，如图6b所示；图6c为t=2s时的原始图像。

在悬臂梁上B点位置处加装ICP压电式加速度传感器，使用LabView软件进行悬臂梁在锤击激励下的振动信号测试。ICP压电式加速度传感器型号为PCB-333B45，频率范围为10～3000Hz，灵敏度为51.7mV/(mm·s-1)，测量时采样频率为1652Hz。测量数据如图7a所示，根据傅里叶变换得到其频率响应，如图7b。

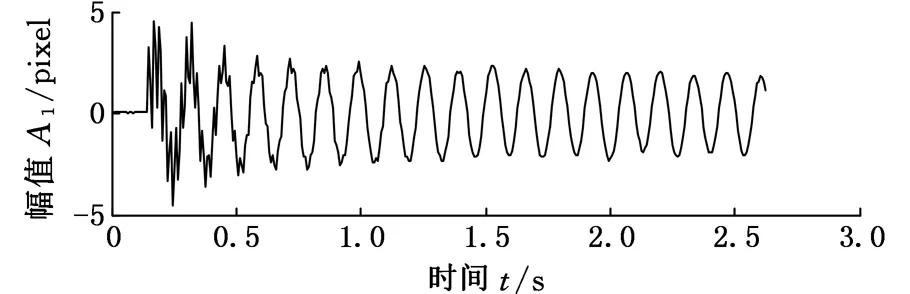
(a)时域响应信号

(b)频率响应

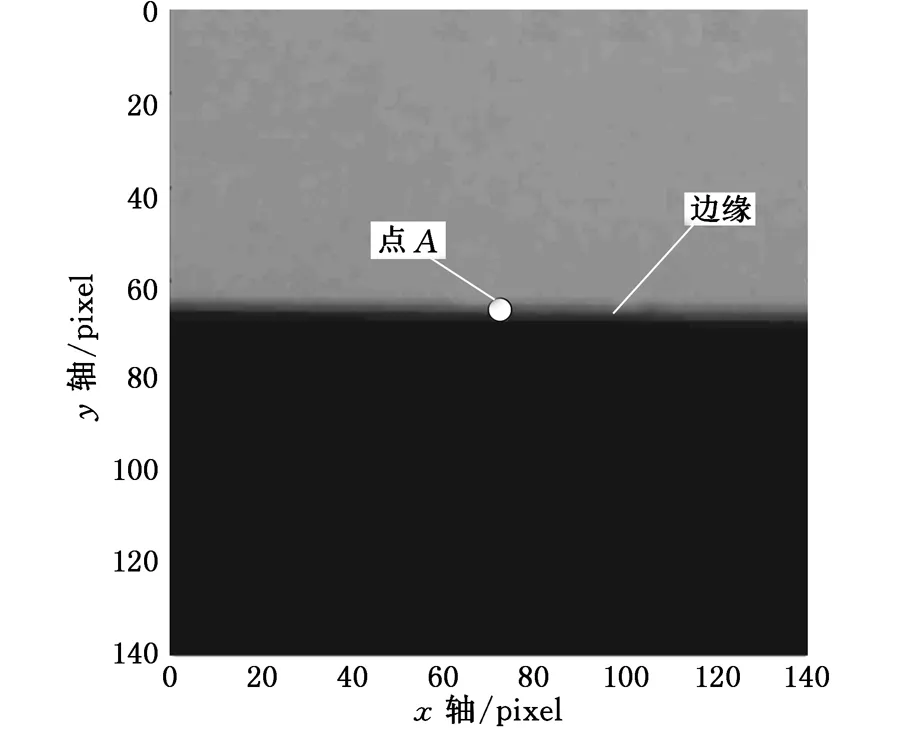
(c)原始图像图6　A点冲击响应频率特性及原始图像

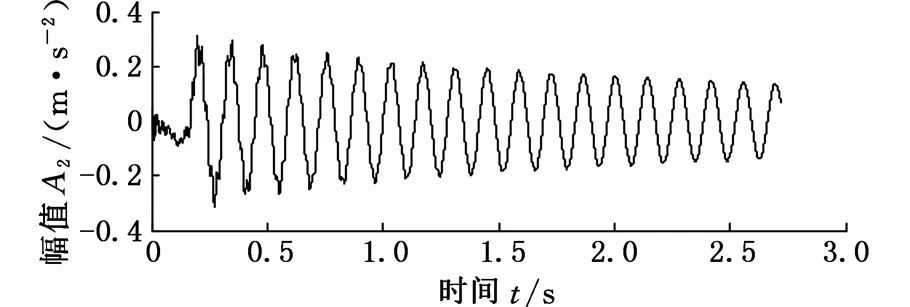
(a)加速度传感器时域响应信号

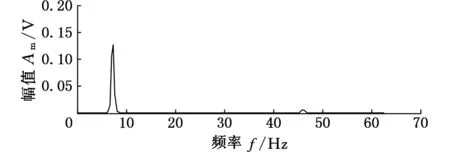
(b)加速度传感器频率响应图7　加速度传感器时域响应信号和频域响应

由系统频率响应得到该试样的一阶、二阶固有频率。表1为该悬臂梁的一阶、二阶固有频率与ANSYS有限元分析的结果对比。由表1可以看出，检测结果与仿真结果基本一致。由于在悬臂梁结构上加装了加速度传感器，故在一定程度上降低了结构固有频率，导致检测频率偏低。对比本文视觉测量方法的数据和传统传感器法的数据可知，视觉测量方法准确有效地测量出了悬臂梁的一阶、二阶振动频率。

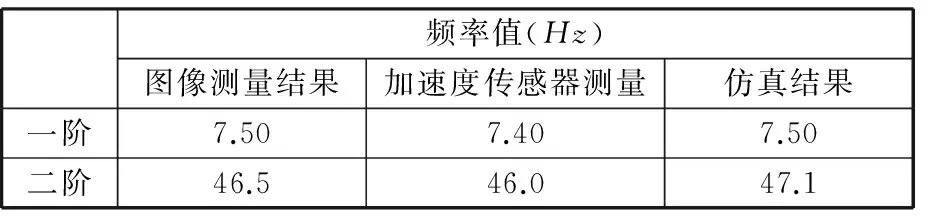
表1　实验与仿真结果对比

2.2.2振型检测

为了提高振动测量图像分辨率，采用650pixel×200pixel分辨率，帧率为60帧/s进行脉冲激励实验。由于相机视场限制的原因，将悬臂梁在x方向分成3等份(OA、AB、BC)，如图4所示，分三次用CCD相机采集每段梁的离面振动图像信息。三次实验中，均在B点脉冲锤击激励。每段梁在特征线上等间距选取13个点作为响应特征点，根据模态参数识别的理论方法，由其冲击响应得到三个一阶振型向量X1(OA段)、X2(AB段)、X3(BC段)。图8为AB段梁的一阶振型向量X2(未归一化)以及点10处的时域响应图和频谱图。图9为三段梁分别在三次激励下所得的一阶振型向量。

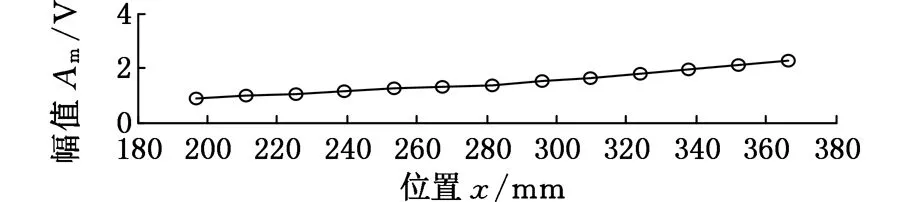
(a)AB段的振型向量

(b)点10处时域响应

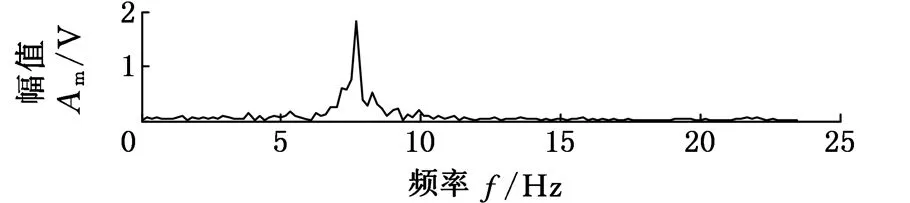
(c)点10处幅值频谱图8　AB段梁的振型向量和点10处的时域响应图、频谱图

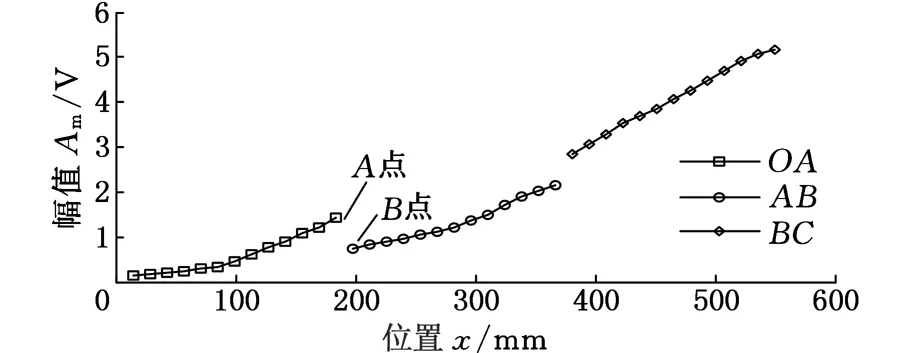
图9　OA、AB、BC三段梁的振型向量

由式(5)及式(6)可知，在理想脉冲激励下，系统第r阶振型向量可由各点该阶脉冲响应函数值得到。由图3可知，在60Hz采样频率范围内，脉冲激励频率特性为常数。由式(4)可知，在三次实验中，不同大小的脉冲激励信号(不同大小的fp)对系统响应的影响只是在响应幅值上相差一个比例常数，且结构的振型是连续的，故设悬臂梁的一阶振型向量为

φ1=(X1，αX2，βX3)T

(8)

其中，α、β为比例常数。

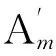
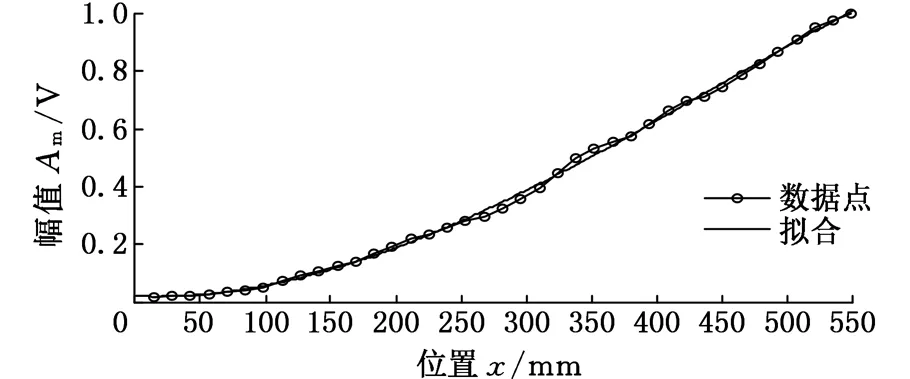
图10　悬臂梁的一阶振型向量及其拟合曲线

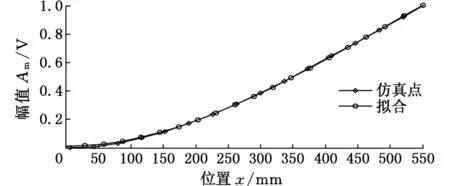
图11　有限元仿真分析与实测拟合曲线对比

3　结语

视觉测量方法具有非接触、大范围测量等优点。本文提出一种常规成像条件下的离面视觉测量方法，实现单相机下的结构离面振动分析。通过对悬臂梁实际测量分析，及与有限元仿真数据对比分析可知，该方法能够以较高的精度进行结构固有频率、振型等振动参数的检测。

本文提出的离面视觉测量方法仍需在如下方面进行研究：① 由于相机帧率的限制，仅进行了前两阶固有频率和一阶振型的测量，对于高频振动难以测量；② 利用边缘提取获取振动信息具有局限性，在复杂结构上不易应用，应研究更一般的图像特征提取方法；③ 结合平面和离面测量，建立三维成像模型，进行三维振动的测量；④在本文实验中，假定力锤的输入信号为理想脉冲信号，对测量结果有一定影响；⑤后续工作将对离面视觉振动检测的应用场合、检测极限、相机分辨率等进行深入分析研究。

[1]李德葆,陆秋海. 实验模态分析及其应用[M]. 北京: 科学出版社, 2001.

[2]张广军. 视觉测量[M]. 北京: 科学出版社, 2008.

[3]王超峰,刘利，汪国保，等. 高频振动方向和振幅测量的模糊图像处理方法[J]. 振动与冲击, 2006, 24(5): 59-62.

Wang Chaofeng, Liu Li,Wang Guobao,et al. Processing Method of High Frequency Vibration Amplitude and Direction Measurement of Fuzzy Image Processing Method[J].Journal of Vibration and Shock,2006, 24(5): 59-62.

[4]季云峰. 无目标计算机视觉技术在斜拉索振动测试中的应用研究[J]. 振动与冲击, 2013, 32(20):184-202.

JI Yunfeng. Application of Non-target Computer-vision-based Technique in Stay-cable Vibration Measurement[J].Journal of Vibration and Shock,2013, 32(20):184-202.

[5]Jing X,Shao L,An W,et al.An Absolute Phase Technique for 3D Profile Measuremen Tusing Four-step Structured Light Pattern[J].Optics and Lasersin Engineering, 2012, 50: 1274-1280.

[6]Teyssieux D, Euphrasie S, Cretin B. MEMS In-plane Motion/Vibration Measurement System Based CCD Camera[J]. Measurement, 2011, 44(10): 2205-2216.

[7]Wang W, Mottershead J E. Frequency Response Functions of Shape Features from Full-field Vibration Measurements Using Digital Image Correlation[J]. Mechanical Systems and Signal Processing, 2012, 28: 333-347.

[8]Seungbae P, Chirag S, Jae K, et al.Transient Dynamic Simulation and Full-field Test Validation for a Slim-PCBOf Mobile Phone under Drop/Impact[C]//Electronic Components and Technology Conference. Reno, 2007: 914-923.

[9]王宏伟,赵国庆，王玉军. 物体振动幅度的远距离非接触测量技术[J]. 振动与冲击, 2009,28(11):67-69.

Wang Hong wei, Zhao Guoqing, Wang Yujun. No-ncontact Measurement Technology for Vibration Detection of Distant Object[J]. Journal of Vibration and Shock, 2009,28(11):67-69.

[10]Réthoré J, Morestin F, Lafarge L, et al. 3D Displacement Measurements Using a Singlecamera[J]. Optics and Lasers in Engineering, 2014, 57: 20-27.

[11]徐飞鸿, 林皓. 单目CCD离面位移测量[J].长沙理工大学学报(自然科学版), 2013, 10(1):54-60.

Xu Feihong,Lin Hao.Out-of-plane Displacement Measurement Based on Single CCD[J]. Journal of Changsha University of Science and Technology(Natural Science), 2013, 10(1):54-60.

[12]孙伟,何小元，郑翔,等. 基于数字图像相关的三维刚体位移测量方法[J]. 光学学报, 2008,28(5): 894-901.

SunWei,HeXiaoyuan,ZhengXiang,et,al.ThreeDimensionalRigidBodyDisplacementMeasure-mentBasedonDigitalImageCorrelation[J].ActaOpticaSinica,2008,28(5): 894-901.

[13]张根辈, 臧朝平. 基于振动测试的非线性参数识别方法[J]. 振动与冲击, 2013,32(1):83-88.

ZhangGenbei,ZangChaoping.ANovelMethodforNonlinearParametricIdentificationBasedonVibrationTests[J].JournalofVibrationandShock,2013,32(1):83-88.

[14]段虎明. 实验模态分析的前端信号精度研究及虚拟式模态分析仪的研制[D]. 重庆：重庆大学, 2008.

(编辑卢湘帆)

AnalysisofStructureVibrationBasedonOut-of-planeMonocularVision

YuQibing1YinAijun2XueLei2ZhangQuan2

1.ResearchCenterofSystemHealthMaintenance,ChongqingTechnologyandBusinessUniversity,Chongqing,400067 2.StateKeyLaboratoryofMechanicalTransmissions,ChongqingUniversity,Chongqing,400044

Conventionalvisionmeasurementhadproblemsofcomplexsystemorlargeamountofcalculations.Themeasurementprinciplesofout-of-planevisionwereresearched.Andcombiningthetheoryofmodalanalysis,thestructuralvibrationparameterswereidentifiedbyaCCDcameraunderthenormallightconditions.AndcomparedtheexperimentalresultsandANSYSshowsthemethodcanmeasurethestructurevibrationparameters(naturalfrequency,dampingandvibrationmode)accurately.Thefutureresearchesofthismethodweregivenintheendofthepaper.

out-of-planevision;visualmeasurement;vibrationparameteridentification;vibrationmode

2015-10-26

国家自然科学基金资助项目(51105396)；装备系统服役健康保障国际联合研究中心开放基金资助项目(KFJJ201501002)；重庆市科委项目(cstc2015jcyjA70007)

TH113

10.3969/j.issn.1004-132X.2016.17.016

喻其炳，男，1972年生。重庆工商大学装备系统服役健康保障国际联合研究中心高级工程师。研究方向为机械设计与制造。尹爱军(通信作者)，男，1978年生。重庆大学机械工程学院教授、博士研究生导师。薛磊，男，1990年生。重庆大学机械工程学院硕士研究生。张泉，男，1991年生。重庆大学机械工程学院硕士研究生。