基于模糊信息公理的产品功能需求优化方案选择

耿秀丽　董雪琦

上海理工大学,上海,200093



基于模糊信息公理的产品功能需求优化方案选择

耿秀丽董雪琦

上海理工大学,上海,200093

采用质量功能展开将顾客需求及重要度转化为产品功能需求及其重要度, 以信息公理为依据，选择信息量最小的功能需求配置方案。采用三角模糊数处理不确定性的质量功能展开信息，采用相对偏好关系分析进行质量功能展开计算，运用模糊信息公理计算定性功能需求的信息量。考虑功能需求间的非线性补偿关系，以总信息量最小化为目标建立0-1非线性规划模型。最后以某装载机功能需求方案规划为例，验证了所提出方法的有效性。

信息公理；质量功能展开；模糊理论；相对偏好关系；非准确性计算

0　引言

产品方案规划是方案设计的首要环节。方案规划是将顾客需求转换为功能需求，包含顾客需求及其重要度分析、功能需求及其重要度分析、功能需求选择或功能需求实现程度优化三个环节。质量功能展开(quality function deployment，QFD)是顾客需求驱动的产品设计方法，其目的在于将顾客需求转化为产品的技术或工程要求。

常见基于QFD计算的规划模型用来在产品规划阶段优化产品功能需求的实现程度或者选择合理的功能属性。Delice等[1]基于QFD方法建立了混合整数线性规划模型，确定连续型产品功能属性的实现程度和离散型产品功能需求的规格。Geng等[2]将KANO模型引入QFD方法，建立了非线性规划模型确定产品服务系统的功能需求实现程度。鲍宏等[3]提出一种面向多样性及绿色性需求满意的产品配置设计方法，基于QFD方法建立了面向客户满意度的绿色产品配置优化模型。这些方法进行功能优化的目标函数是顾客满意度最大化，顾客满意度的衡量有两类方法。一类方法是将功能需求实现程度与重要度的乘积和近似作为顾客满意度[4-5]，这类方法难以确定功能需求实现程度与具体属性取值的关系；另一类方法是借助KANO理论计算所选功能需求对应的顾客满意度[6]，这类方法难以确定所选功能需求在KANO曲线上的位置，确定顾客满意度的主观性强。

信息公理是指在各功能需求相互独立的条件下，信息量最小的设计方案为最佳设计方案，可以不需要决策者给出指标的权重，避免了人为主观因素的影响。目前信息公理已在产品、服务和制造系统等领域的方案评价中得到了广泛应用。Chen等[7]考虑决策环境的模糊性和不确定性，将方案指标的设计域和系统域分别表示为模糊变量和随机变量，提出了期望信息量计算模型计算方案指标的信息量。童一飞等[8]提出了基于信息公理与粗集理论的多属性模糊优选方法，采用模糊信息公理方法对网格资源进行定量评价，以选出最佳资源。王浩伦等[9]针对评价信息主观性和不确定性的情况，将专家语言评估信息转化为二元语义形式，根据信息公理思想计算零件材料的二元信息量来对其进行排序和优选。功能需求一般分为定量需求和定性需求。对于定量功能需求，可以根据信息公理计算其信息量并选出最优。对于定性功能需求，往往采用不确定性语义术语进行评估，不能给出确定的数值来计算其信息量，模糊信息公理通过隶属函数来计算信息量，采用三角模糊数表达并处理功能需求重要度，解决了定性功能需求信息量的求值问题，同时，通过将不确定性语言信息数值化提高了选择的准确性。本文以功能需求组合的信息量最小为目标函数，构建规划模型实现产品功能需求优化方法的选择。

为考虑功能需求间的补偿关系，本文采用非准确性计算思想通过引入补偿因子s，建立以功能需求组合的信息量为最小的非线性QFD规划模型。本文运用文献[10]的非准确性计算思想，根据属性权重和补偿因子s将多属性决策问题转化为单属性决策问题，通过将补偿因子的取值范围扩展至无穷，得到更大范围的集成结果。

为解决QFD中评价信息的主观性和不确定性问题，本文采用三角模糊数表达并处理顾客需求重要度以及顾客需求与功能需求间的关联关系，并以模糊QFD方法解决两组三角模糊数间的乘积计算问题。Li等[11]针对模糊QFD问题，分别提出关联关系和自相关关系确定的粗糙集方法，进而确定产品工程特性的初始重要度。Wang等[12]将相对偏好关系分析用于功能需求选择的模糊QFD分析中，解决了两个模糊数相乘困难的问题。

本文提出基于模糊信息公理的产品功能需求优化方案选择方法，首先通过模糊QFD方法分析顾客需求，获取产品的功能需求；然后采用相对偏好关系分析计算功能需求的相对重要度；最后引入模糊信息公理计算可选功能需求的信息量，采用非准确性计算思想建立以总信息量最小为目标的非线性规划模型，实现功能需求优化方案的选择；以某企业装载机的方案规划为例，验证所提方法的有效性。

1　研究框架

方案规划过程是将顾客需求转换为产品功能需求并选择合适功能需求的过程，QFD是实现顾客需求转向功能需求的有效方法和工具。产品功能需求优化方案的目标是选择出总信息量最小的产品功能需求优化方案。本文所提基于模糊信息公理的产品功能需求优化方案选择的思路如图1所示。具体步骤如下：

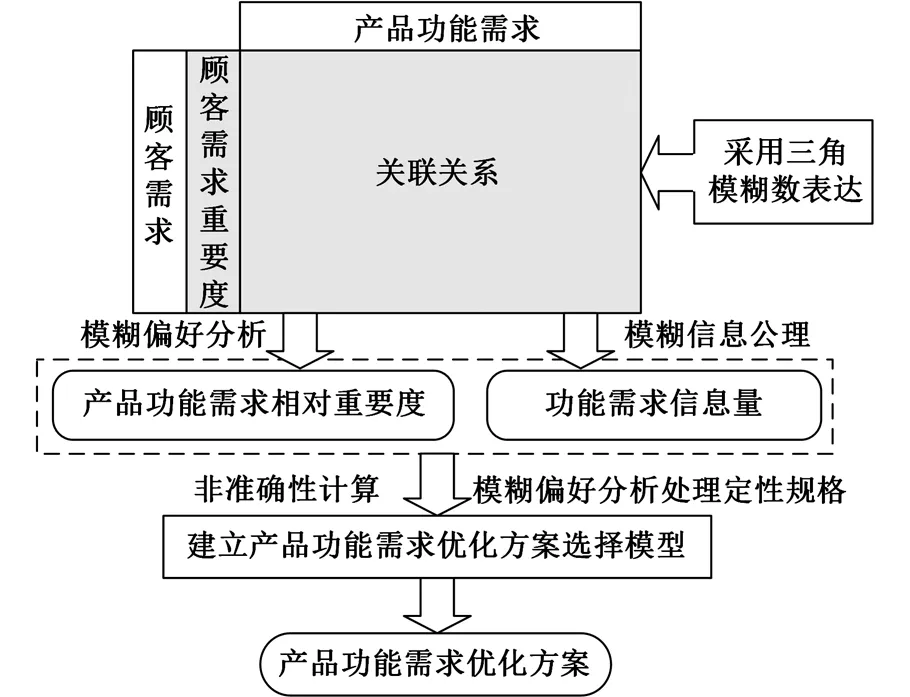
图1　基于模糊信息公理的产品功能优化方案选择思路

(1)专家采用语义评价术语对顾客需求重要度以及顾客需求与功能需求间的关系进行评价，然后采用三角模糊数对评价结果进行计算，得到顾客需求的模糊重要度、顾客需求与功能需求间的模糊关系矩阵以及各个功能需求的相应隶属函数。

(2)采用模糊偏好分析将顾客需求的重要度转化为精确数值。根据QFD方法计算功能需求的模糊重要度，然后采用模糊偏好分析得到功能需求的相对重要度。

(3)根据隶属函数确定各功能需求的模糊系统范围和模糊设计范围，求出各功能需求的信息量。

(4)考虑各功能需求间的非线性补偿关系，运用非准确性计算方法建立以总信息量最小为目标的0-1非线性规划模型，在成本约束的条件下求解找出最优方案。

2　模糊信息公理

2.1模糊信息公理概念

信息公理是指信息量最小的设计方案为最优设计方案。信息量I由满足给定功能需求的概率来确定，若满足给定功能需求的成功概率为P，则与概率有关的信息量为[13]

I=-log2P

(1)

其中，成功概率P可由设计范围RD和系统范围RS确定，设计范围是满足期望值的范围，系统范围是功能需求指标值的确切分布范围。而系统范围和设计范围的交集部分，为公共范围RC，因此，信息量I也可以表示为[14]

(2)

在设计方案中，往往会有一些模糊性功能需求，不能通过给出具体数值来计算其信息量，一般只能用模糊性语言来描述，如“好”“一般”“差”等。而对于这种模糊评价指标，本文将每种语义表达形式都表示成一定的设计或系统范围，并以隶属函数的形式表示，如图2所示。

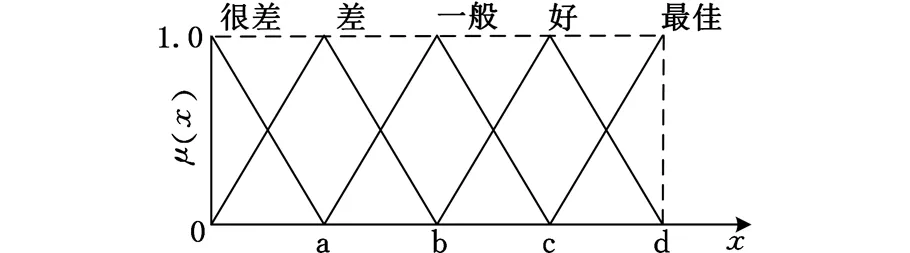
图2　三角形隶属度函数曲线

方案中对于定量功能需求，一般直接运用信息量的计算公式得出信息量，但对于定性功能需求，则需要运用模糊信息公理计算其信息量，本文将设计范围的隶属函数曲线所围成的面积定义为模糊设计范围RFD，系统范围的隶属函数曲线围成的面积定义为模糊系统范围RFS，它们的交集所围成的面积定义为模糊公共范围RFC，如图3所示。因此，模糊信息量的计算公式为

(3)

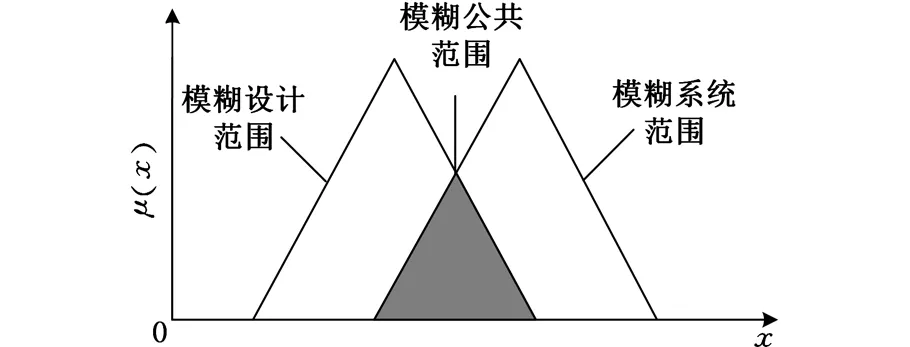
图3　模糊设计范围、模糊系统范围和模糊公共范围示意图

对于某选择方案而言，当功能需求评价值与评价目标值一致时，即其模糊系统范围刚好与其模糊设计范围重合，此时信息量为零，则该方案对于此项功能需求是理想的。当评价值和评价目标值不重合时，信息量无穷大，则该方案对于此项功能需求是不理想的。

2.2信息量计算

功能需求可分为效益型(属性值越大越好)和成本型(属性值越小越好)。不同类别的功能需求采用不同的信息量计算方法。当某个功能需求的属性值是一个实数时，假设第i个功能需求的属性值为xi，最佳属性值为x01，最劣属性值为x02，那么满足功能需求的概率P=xi/x01。对于效益型，其候选规格的信息量为[15]

(4)

成本型功能需求对应的信息量为[15]

(5)

假设已知某个功能需求的设计范围，当其属性值为具体实数时，式(2)就不再适用。因为当其属性值落在设计范围内，其信息量为0，落在范围外，其信息量为无穷大。如对某效益性功能需求，其设计范围为50～80，某一属性值为60，则系统范围为50～60，公共范围也是50～60，此时公共范围等于系统范围，其信息量为0。另一属性值为70，其系统范围是50～70，公共范围也是50～70，信息量为0。两个属性值的信息量相等，但实际上70明显要优于60，这与实际情况不符。因此就需要对信息量的计算公式做一定修改，信息量的计算式应改为

(6)

对应的模糊信息量应该改为

(7)

3　基于模糊偏好分析的QFD分析

3.1采用三角模糊数处理QFD中的不确定性语义信息

假设通过访谈和调研获取的产品功能需求优化方案中的顾客需求为Ci(i=1,2,…,m)，功能需求为Mj(j=1,2,…,n)。由专家Ek(k=1,2,…,q)采用语义评价术语对顾客需求重要度以及顾客需求和功能需求间的关联关系进行评价，然后采用三角模糊数对专家给出的语义评价信息进行处理。

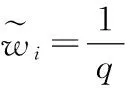
(8)

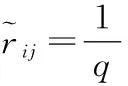
(9)

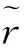
(10)

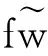
(11)

3.2采用模糊偏好分析计算功能需求的相对重要度

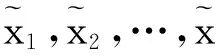
该组三角模糊数的均值为

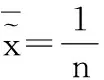
(12)

相对偏好分析采用Up*算子，通过计算组中每个三角模糊数和均值的相对偏好关系，将每个三角模糊数转化为精确数值。Up*算子的公式如下[12]：

(13)

其中

‖T‖=

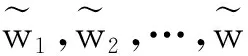
4　产品功能需求选择

在产品功能需求优化方案规划时，除了要考虑功能需求的信息量外，还需要考虑各项功能需求的成本因素以及相对重要度。由专家给出各项功能需求的成本以及总预定成本，要求在满足成本条件的情况下找到信息量最小的设计方案，建立0-1非线性整数规划模型。

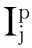
基于上述问题的描述和参数的说明，以信息量ys最小为目标，在约束条件下建立0-1线性规划模型：

(14)

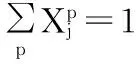
由于产品功能需求Mj间存在补偿关系，非准确性计算考虑功能需求间的补偿关系，可以计算不同补偿水平下的总信息量，提高选择结果的可靠性和准确性。考虑各功能需求间补偿关系的功能需求,选择0-1非线性规划模型：

(15)

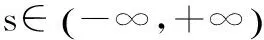
s.t.,　　∀j

其中,s为功能需求间的补偿因子。当s→-∞时补偿水平最低，即功能需求间不存在补偿关系，这时总信息量受限于最低性能的功能需求，此时其他具有高性能的功能需求对该功能属性不存在补偿关系。s=0时功能需求间存在完全补偿关系。高性能的功能需求对低性能的功能需求存在补偿关系，此时总信息量为各功能需求属性值的几何平均。s>0时功能需求间存在超补偿关系，当s=1时总信息量为各功能需求属性值的加权平均，当s→+∞时总信息量由具有最高性能的功能需求决定。

5　案例分析

某机械厂欲对其装载机进行功能升级，以满足不同市场需求层次的顾客需求，提高企业利润。因此要选用合适的规划方案来对企业产品进行设计。通过顾客访谈和调研获取的顾客需求包括：动力强劲(C1)、灵活高效(C2)、易操控(C3)、稳定可靠(C4)、服务及时(C5)、低能耗(C6);相关的功能需求有发动机额定功率(M1)、最大掘起力(M2)、斗容量(M3)、最大卸载高度(M4)、三项和时间(M5)、最小转弯半径(M6)、变速操纵方式(M7)、预防性维修策略(M8)、服务响应效率(M9)、服务完成效率(M10)、节能方案(M11)、尾气排放标准(M12)。由于企业设计专家、售后专家和顾客均对顾客需求有较深的了解和不同的看法，因此选择10位企业产品设计工程师、10位售后服务工程师和20位领先用户企业专家组成专家组对顾客需求重要度进行语义评价，然后利用表1中语义变量与三角模糊数的转换关系，将语义评价结果转换成由三角模糊数表达的顾客需求模糊重要度。利用式(12)～式(13)计算顾客需求的相对重要度，将顾客需求模糊重要度转化成精确数值，计算结果如表2所示。

同样，专家组对顾客需求重要度与功能需求间的关联关系进行语义评价，利用表1中的转换关系将语义评价结果转化成顾客需求与功能需求间的模糊关联关系，如表3所示。将顾客需求和功能需求间的模糊关联关系依次记录在表4中，得到顾客需求和功能需求间模糊关联关系矩阵。

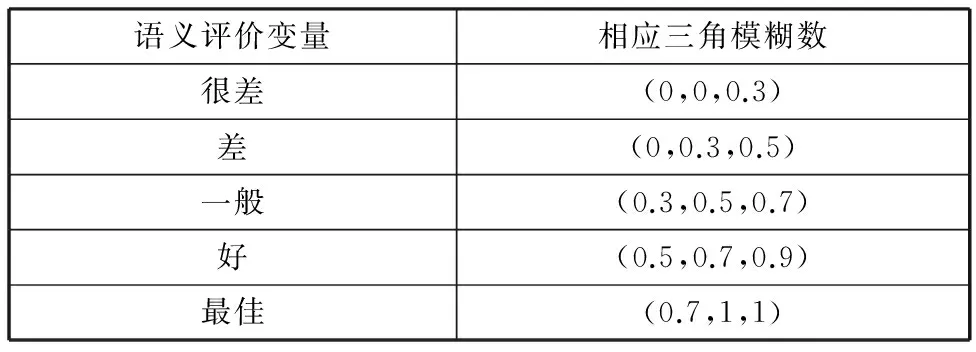
表1　语义评价变量与三角模糊数的转化关系

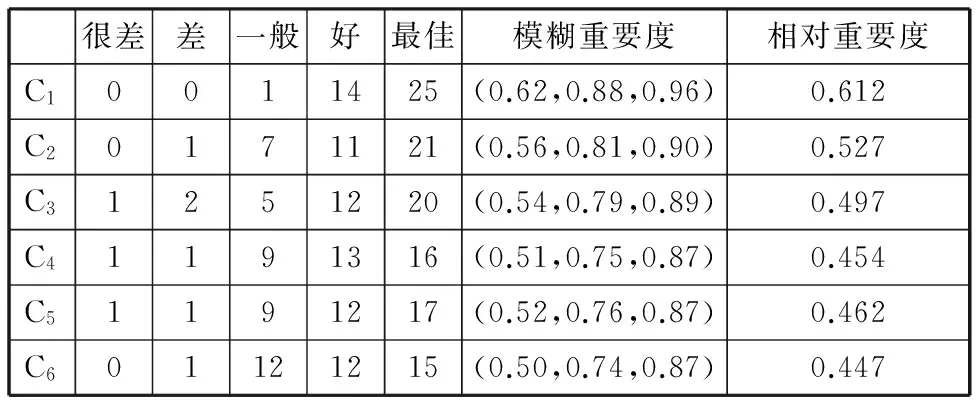
表2　顾客需求重要度的语义评价及其相对重要度

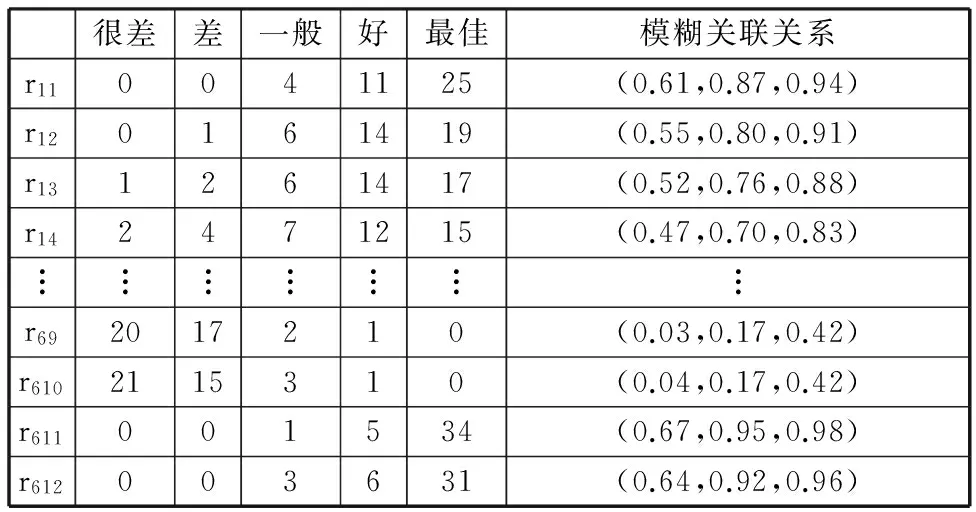
表3　顾客需求和功能需求关联关系的语义评价

根据表2中的顾客需求相对重要度和表4中顾客需求和功能需求间的模糊关联关系矩阵，利用公式(11)计算得到功能需求的模糊重要度。采用相对偏好关系分析，用式(12)～式(13)计算得到的12个功能需求的相对重要度为:0.619，0.580，0.545，0.502，0.481，0.410，0.492，0.480，0.481，0.468，0.485，0.455。表5为该企业的装载机方案规划的功能需求可选项及其相应成本。

根据信息公理及模糊信息公理求出每一个功能需求候选规格的信息量。根据顾客需求确定定性功能需求的设计范围：变速操纵方式(M7)自动变速为最佳，电液操纵为好，液压操纵一般，机械操纵为一般，设计范围要求一般以上。机械操纵预防性维修策略(M8)策略1为一般，策略2为好，策略3为最佳，设计范围要求一般以上。节能方案(M11)方案1为一般，方案2为一般，方案3为好，设计范围要求一般以上。尾气排放标准(M12)国一和国二为一般，国三为好，国四为最佳，设计范围要求一般以上。需要将其模糊重要度三角模糊数转换为隶属函数，根据公式(7)求出其模糊信息量。以变速操纵方式(M7)为例，给出其模糊信息量计算过程，其余各功能需求的信息量仅列出其计算结果，如表6所示。

表4　顾客需求和功能需求间的模糊关联关系矩阵

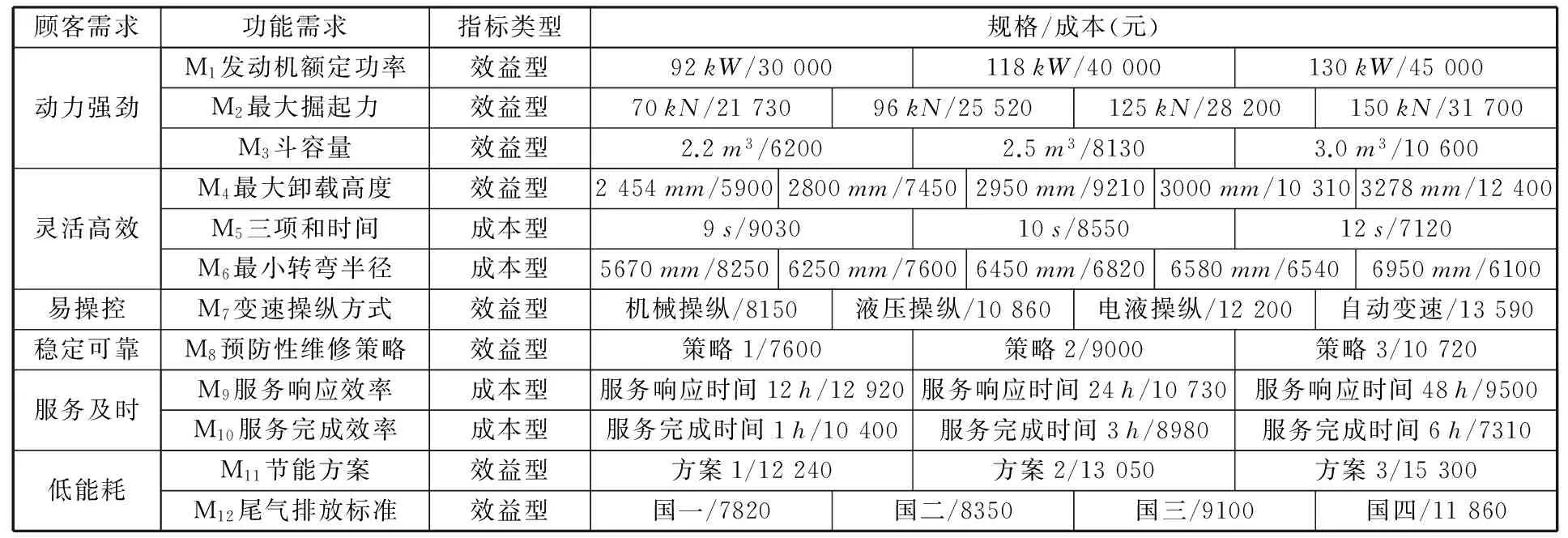
表5　功能需求候选规格及相应成本

变速操纵方式(M7)设计范围一般以上，机械操纵的为一般，其模糊设计范围隶属函数围成的面积为0.5，模糊公共范围隶属函数围成的面积为0.2，作出其三角隶属函数如图4所示，根据式(7)计算其模糊信息量为log2(0.5/0.2)=log22.5=1.3219。

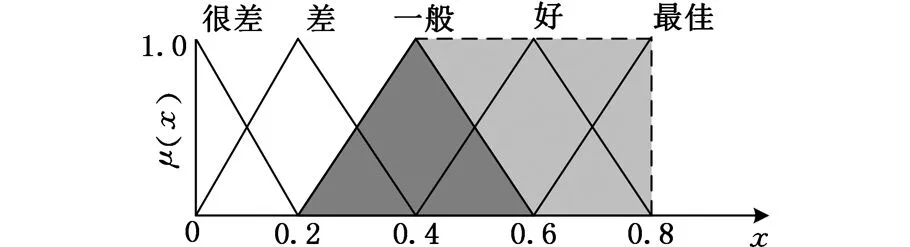
图4　变速操纵方式的隶属函数曲线

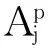
由计算结果可知，其他条件固定的情况下，只改变成本约束，随着成本的提升,各功能需求尤其是信息量小的属性更倾向于选配更优的属性值，如M2、M6、M7、M8等随着总成本的上升其属性值也变得更优，这与实际情况相符。图5给出了不同成本约束条件下，功能需求优化方案选择对比情况。候选规格表示选取功能需求Mj对应的第p个属性值。

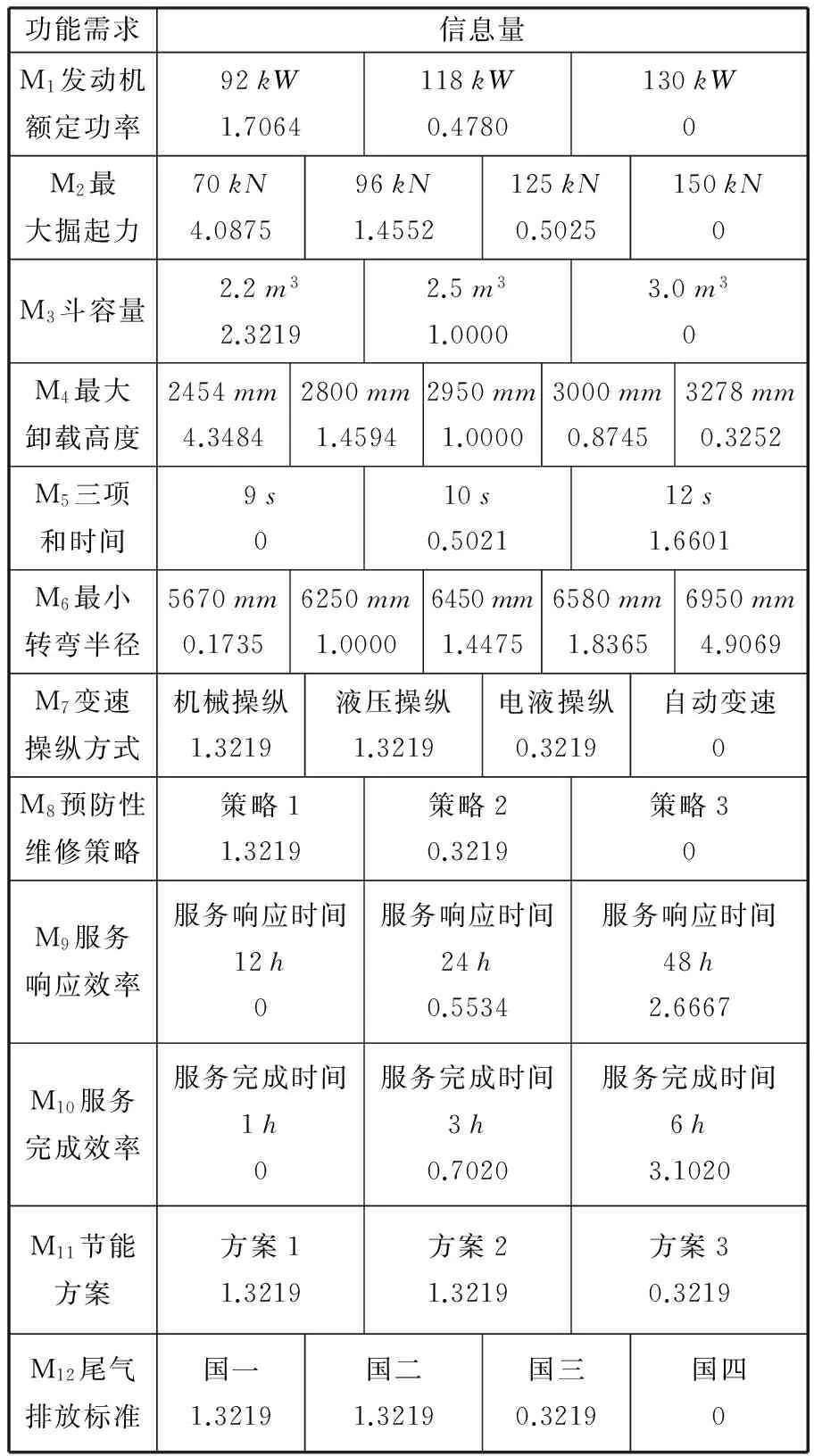
表6　功能需求候选规格的信息量

表7　不同成本下的功能需求优化方案

在成本都为18万的情况下，计算不同补偿水平下的装载机功能需求选择方案，结果如表8所示。其计算结果对比情况如图6所示。

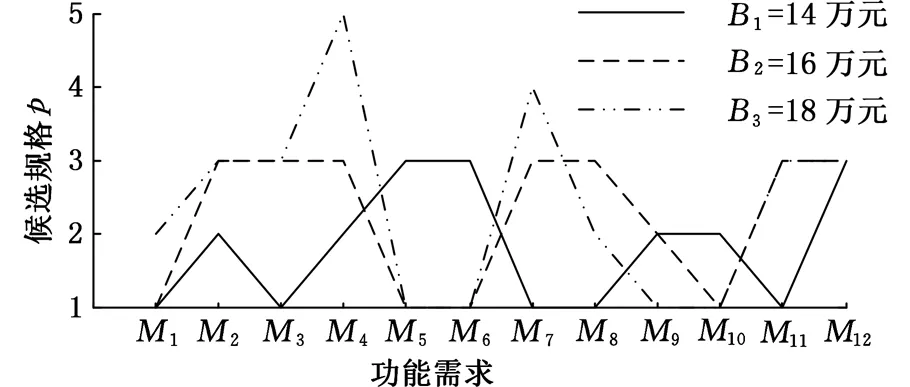
图5　不同成本约束条件功能需求优化方案选择对比图

补偿因子s=-1s=1补偿因子s=-1s=1M1A11A21M7A47A47M2A42A32M8A38A28M3A33A33M9A19A19M4A54A54M10A110A110M5A15A15M11A311A311M6A16A16M12A412A312

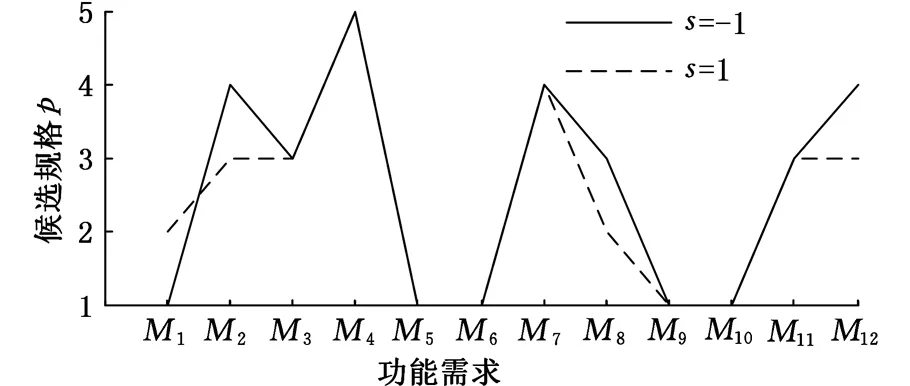
图6　不同补偿水平下功能需求选择方案对比图

根据表8可知，在成本及其他约束相同的情况下，随着补偿因子的增加，相对重要度较大的功能需求更倾向于信息量更小的属性值，相对重要度较小的功能需求更倾向于信息量大的属性值，例如，当补偿因子从-1变为1时，发动机额定功率从92kW提高到118kW，而尾气排放标准从国四降成国三，这与定性分析结果一致。

在补偿因子相同且成本相同的情况下，调整顾客需求重要度，给出三组不同的顾客需求重要度，其中：Wa为原始的顾客需求重要度，Wb和Wc为 另 外 给 出 的 两 组 参 照 组 ，Wb为 {0.800,0.700,0.600,0.500,0.400,0.300}, Wc为{0.300,0.400,0.500,0.600,0.700,0.800}。计算在相同补偿因子 s=1 和相同成本约束B2=18万元的条件下的选配方案，结果如表9所示，其计算结果对比图见图7。根据计算结果可知，当顾客需求变化时，最终产品功能需求选择也会变化。当某一顾客满意度增大，与其关联性较强的功能需求更倾向于选择更优的属性值。反之，则会选择较劣属性值。例如，当C4(服务及时)重要度由0.454升为0.700时，与其具有较强关联关系的M8(预防性维修策略)

表9不同顾客需求重要度下的功能需求优化方案

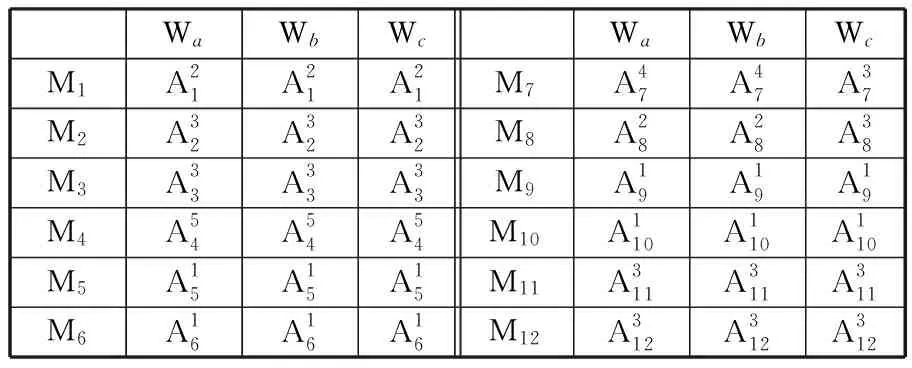
WaWbWcWaWbWcM1A21A21A21M7A47A47A37M2A32A32A32M8A28A28A38M3A33A33A33M9A19A19A19M4A54A54A54M10A110A110A110M5A15A15A15M11A311A311A311M6A16A16A16M12A312A312A312

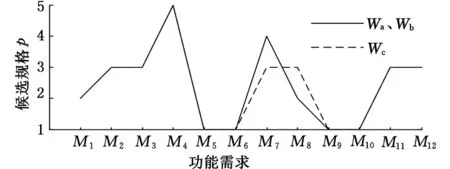
图7　不同顾客需求重要度下功能需求选择方案对比图

由原来的策略2变为策略3，性能上升。

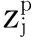
成本型功能需求的实现程度：

表10　所提方法与对比方法的方案优化结果

对于定性指标，如候选规格有5个，则从好到差依次用5～1表示；如候选规格有4个，则从好到差依次用4～1表示；如候选规格有3个，则从好到差依次用3～1表示；然后再计算其实现程度。在相同补偿因子 s=1 和相同成本约束 B2=16万元的条件下，对比方法的选配方案与本文所提方法的结果如表10所示。根据结果对比图(图8)可以看出本文所提基于模糊信息公理的选配方案中最大掘起力M2=125kN，最大卸载高度M4=2950mm，分别优于采用传统基于需求实现程度的优化结果M2=70kN和M4=2800mm，说明本文所提方法具有明显优势。

图8　不同方法下装载机功能需求优化方案选择结果对比图

6　结论

(1)在功能需求选择的QFD分析过程中，充分考虑了信息的模糊性和不确定性，结合模糊集方法和相对偏好关系分析，计算模块属性重要度。引入模糊信息公理，计算各功能需求的信息量。

(2)考虑了功能需求间可能存在的非线性补偿关系，采用非准确性计算的方法，以总信息量最小为目标，成本为约束，建立了0-1非线性规划模型。

(3)通过对国内某机械制造企业装载机功能需求优化选择方案的研究分析，表明了所提方法的有效性与可行性。

[1]Delice E K, Güngör Z. A New Mixed Integer Linear Programming Model for Product Development Using Quality Function Deployment [J]. Computers & Industrial Engineering, 2009, 57(3):906-912.

[2]Geng X, Chu X, Xue D, et al. A Systematic Decision-making Approach for the Optimal Product-service System Planning [J]. Expert Systems with Applications, 2011, 38(9):11849-11858.

[3]鲍宏, 刘光复, 张雷,等. 面向多样性和绿色性需求满意的产品配置设计[J]. 中国机械工程, 2012, 23(7):815-822.

Bao Hong ,Liu Guangfu, Zhang Lei,et al. Product Configuration Design Oriented to Satisfaction for Diversity and Green Requirements[J]. China Mechanical Engineering，2012, 23(7):815-822.

[4]Chen L H, Ko W C, Tseng C Y. Fuzzy Approaches for Constructing House of Quality in QFD and Its Applications: a Group Decision-making Method[J]. IEEE Transactions on Engineering Manage-ment, 2013, 60(1):77-87.

[5]Xue X, Wu L, Liu Y, et al. Study of System-level Electromagnetic Compatibility Indicator Process Based on QFD[C]// 10th International Symposium on Antennas, Propagation & EM Theory(ISAPE). Xi’an, 2012:1064-1068.

[6]Hashim A M, Dawal S Z M. Kano Model and QFD Integration Approach for Ergonomic Design Improvement [J]. Procedia-Social and Behavioral Sciences, 2012, 57:22-32.

[7]Chen D, Chu X, Sun X, et al. An Information Axiom Based Decision Making Approach under Hybrid Uncertain Environments [J]. Information Sciences, 2015, 312:25-39.

[8]童一飞,李东波,于敏建,等.基于信息公理与粗集理论的多属性模糊优选研究[J].中国机械工程, 2007, 18(17):2029-2033.

Tong Yifei,Li Dongbo,Yu Minjian,et al. Research on Multi-attribute Fuzzy Optimal Selection Based on Information Axiom and Rough Set[J].China Mechanical Engineering, 2007, 18(17):2029-2033.

[9]王浩伦,徐翔斌,周尔民.基于二元语义信息公理的汽车零件材料选择[J].中国机械工程, 2015,26(23):3172-3177.

Wang Haolun, Xu Xiangbin, Zhou Ermin. Material Selection of Automotive Components Based on Information Axiom with 2-Tuple Linguistics[J].China Mechanical Engineering,2015,26(23):3172-3177.

[10]Chen Y Z, Ngai E W T. A Fuzzy QFD Program Modelling Approach Using the Method of Imprecision [J]. International Journal of Production Research, 2008, 46(24):6823-6840.

[11]Li Y L, Tang J F, Luo X G, et al. An Integrated Method of Rough Set, Kano’s Model and AHP for Rating Customer Requirements’ Final Importance [J]. Expert Systems with Application, 2009, 36(3): 7045-7053.

[12]Wang Y J. A Criteria Weighting Approach by Co-mbining Fuzzy Quality Function Deployment with Relative Preference Relation [J]. Applied Soft Computing, 2014, 14:419-430.

[13]Suh N P. The Principles of Design [M]. Oxford: Oxford University Press, 1990.

[14]Suh N P. Axiomatic Design: Advances and Applications [M]. Oxford: Oxford University Press, 2001.

[15]程贤福, 肖人彬, 刘平安,等. 基于信息公理的混合型多属性产品方案评价[J]. 计算机集成制造系统, 2010, 16(9):1816-1822.

Cheng Xianfu, Xiao Renbin, Liu Ping’an, et al. Hybrid Multiple Attributes Evaluation Method for Product Scheme Based on Information Axiom[J]. Computer Integrated Manufacturing Systems, 2010, 16(9):1816-1822.

(编辑王旻玥 )

Optimization of Product Functional Requirements Based on Fuzzy Information Axiom

Geng XiuliDong Xueqi

University of Shanghai for Science of Technology, Shanghai, 200093

QFD was employed to translate the customer requirements (CRs) and their importance degrees into product functional requirements and their importance degrees. Based on the information axiom, the function requirement configuration concept with the least amount of information was selected. Triangular fuzzy number was used to deal with the fuzzy QFD information. The relative preference relation analysis was provided to process the QFD calculation, and fuzzy information was used to calculate the imformation of qualitative functional requirements. Considering the compensation relationships among the function requirements. a 0-1 non-linear programming model was established with the objective of minimizing the amount of information of function requirements. Finally, an example of product functional requirements optimization for loader was given out to demonstrate the effectiveness of the proposed approach.

information axiom; quality function deployment(QFD); fuzzy theory; relative preference relation; method of imprecision

2015-12-16

国家自然科学基金资助项目(71301104，71271138)；高等学校博士学科点专项科研基金资助项目(20133120120002，20120073110096)；上海市教育委员会科研创新项目(14YZ088)；上海市一流学科资助项目(S1201YLXK)；沪江基金资助项目(A14006)

TH122; N94

10.3969/j.issn.1004-132X.2016.17.013

耿秀丽，女，1984年生。上海理工大学管理学院副教授。主要研究方向为产品服务系统、服务科学、决策理论与方法等。发表论文30余篇。董雪琦，女，1993年生。上海理工大学管理学院硕士研究生。