钢筋混凝土核心筒水平双向抗震性能研究[1]

陈 盈 刘 昭 赵 均



钢筋混凝土核心筒水平双向抗震性能研究[1]

陈 盈1，2）刘 昭1）赵 均1，2）

1）北京工业大学建筑工程学院，北京 100124 2）北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京 100124

本文利用ABAQUS有限元分析软件，对双向水平往复荷载作用下的钢筋混凝土核心筒进行非线性分析，将所得结果与现有试验结果对比验证，明确了其破坏形态、承载力、刚度退化和耗能能力等抗震性能。研究结果表明，两个方向受力的耦合作用会导致刚度退化的加剧，降低其抗震性能；通过分析轴压比、连梁跨高比和截面长宽比等参数，并与单向加载下的结果对比，发现轴压比和连梁跨高比均是影响筒体破坏形态的重要因素，且两个方向的刚度差异则会导致筒体变形能力与延性有较大的降低；给出了考虑加载方式、洞口大小以及混凝土强度影响的核心筒在压、弯、剪、扭复合状态下的承载力计算公式，并与现有试验结果对比，吻合较好。

混凝土核心筒 高层建筑 双向水平荷载 抗震性能

引言

钢筋混凝土核心筒由于其在各个方向均有较大的抗侧刚度，是主要的抗侧力构件，并承担大部分水平荷载而成为高层和超高层建筑主要的结构形式（方鄂华等，1999；徐培福等，2005）。目前，国内外对核心筒抗震性能的研究已取得了一些成果，但大多集中在其受水平单向荷载作用下的试验研究（Nakachi等，1996；Atsushi等，2000；赵均等，2006；史庆轩等，2011）和有限元分析（赵均等，2010；侯炜等，2013）。实际震害表明，结构在多维地震动作用下各主轴方向上的反应相互影响，形成耦联，从而导致结构整体抗震性能的降低。因此，研究钢筋混凝土核心筒在双向水平地震作用下的抗震性能就显得尤为重要。近年来，国内已有少量对混凝土核心筒的双向加载下的试验研究成果，如：杜修力等（2012）进行了核心筒在双向水平受力条件下的抗震试验，表明考虑双向加载对核心筒的承载能力有明显影响；许洋等（2013a）针对更大高宽比的试件进行了抗震试验，认为高轴压比下双向加载对于筒体的性能影响更为不利。但由于双向加载规则的不同以及试验条件的限制，各试验之间难以比对，且影响核心筒性能的因素较多，为此有必要结合数值模拟方法分析，通过建立合理的有限元模型，对模型试验进行补充并研究核心筒在双向荷载作用下的受力性能。

本文在现有试验研究的基础上，利用ABAQUS有限元软件，通过改变轴压比、连梁跨高比和截面长宽比等参数，明确钢筋混凝土核心筒在水平双向荷载作用下的抗震性能及其主要影响因素，并建立了考虑加载方式、洞口大小以及混凝土强度影响的核心筒在压弯剪扭复合作用下的承载力计算公式，研究结果可为钢筋混凝土核心筒的工程设计提供参考。

1 抗震性能分析

1.1 试验简介

本文以已有钢筋混凝土核心筒抗震性能试验（许洋，2013b）为研究基础。试件以某大厦钢筋混凝土核心筒为原型，按照约1:7.5的缩尺比例设计，筒身共7层，净高3290mm，筒体横截面轮廓尺寸为1050mm×1050mm，高宽比为3.14，墙体厚度75mm，墙体配置双层钢筋网。对其中的编号为ZJT1和ZJT5试件进行有限元模拟，ZJT1试件采用单向水平低周反复加载，轴压比为0.24；ZJT5试件采用双向水平矩形加载，轴压比为0.15。试件平面配筋图以及加载图如图1所示。

1.2 有限元分析模型

本文采用大型通用有限元软件ABAQUS对核心筒进行非线性有限元模拟，加载方式与试验一致。采用分离式单元建立模型，混凝土采用实体单元C3D8R模拟，钢筋采用三维2节点桁架T3D2单元。混凝土采用弹塑性损伤塑性模型，主要输入参数见表1，其中拉伸和压缩特性采用《混凝土结构设计规范》（GB 50010-2010）提供的应力-应变表达式，损伤因子的定义采用Najar的损伤理论。考虑钢筋达到屈服强度后的强化特性，采用二折线随动强化模型，取钢筋初始弹性模量的1%作为屈服后的弹性模量，其材料属性见表2。

表1 混凝土模型输入参数 Table 1 Input parameters of concrete model

表2 钢筋材料性能 Table 2 Material properties of the rebar

1.3 分析模型的试验验证

对于筒体的开裂及破坏特征通过查看图3和图4中混凝土的受拉、受压损伤因子的变化和分布进行判断，可知计算模型在加载过程中的破坏特征与试验吻合较好。

（a）受拉损伤因子 （b）受压损伤因子

图3 试件ZJT1损伤分布
Fig. 3 Damage factor distribution of specimen ZJT1

（a）受拉损伤因子 （b）受压损伤因子

图4 试件ZJT5损伤分布
Fig. 4 Damage factor distribution of specimen ZJT5

图5为各试件基底剪力-顶部位移曲线。可见，在两种不同加载方式作用下，计算所得的荷载-位移曲线与试验骨架曲线均吻合较好，在单向水平荷载作用下所得结果更趋同于试验值，而在双向水平荷载作用下，试验模型刚度衰减要快于计算模型，导致计算所得屈服荷载及最大荷载均大于试验值，但最大误差不超过10%。考虑到试验中的矩形加载在实现时有一定的误差，而计算模型为理想模型，可以认为该模型比较真实地对钢筋混凝土核心筒的加载过程、破坏特征、承载力及变形能力进行了模拟，是一个比较准确而有效的计算模型。

（a）ZJT1          （b）ZJT5向           （c）ZJT5向

图5 试件基底剪力-顶部位移曲线比较
Fig. 5 Base shear-top displacement vs. biaxial cyclic lateral loading

1.4 单双向荷载作用下的对比

本文对比了轴压比=0.24的核心筒分别在单向、双向水平荷载下的受力性能，包括破坏形态、承载力、耗能能力等。

核心筒在极限破坏状态时的受拉损伤因子分布如图6所示。两种加载方式下破坏均首先表现为连梁两端的竖向裂缝和底层墙肢的水平裂缝，然后连梁中部和墙肢分别出现斜向剪切裂缝。在单向荷载作用下腹板墙肢斜向剪切裂缝明显，连梁破坏严重；翼缘墙体水平裂缝集中在下部，连梁无破坏；而在双向水平荷载作用下，、向墙肢交替充当腹板墙体和翼缘墙体，两个方向墙肢的剪切斜向裂缝和弯曲水平裂缝相互交织，均匀分布，破坏时连梁较单向加载的腹板墙体连梁破坏轻，但墙肢转角处破坏严重。两者的最后破坏形态相同，底部墙肢受拉钢筋屈服后，混凝土压溃，为整体弯曲破坏。

（a）单向 （b）双向

图6 不同加载方式下核心筒损伤因子分布
Fig. 6 Damage distribution of specimen under different load modes

图7为两种加载方式下核心筒的顶部位移-基底剪力曲线对比，各模型特征量如表3所示，包括试件名义屈服时、峰值荷载时、以及极限荷载时的水平荷载和对应的核心筒顶部位移。可见，双向加载时，各特征值均有不同程度的减小，如、方向的极值荷载分别减小了9.4%和17.6%；延性系数分别降低了19.9%和27.0%。说明在双向荷载作用下，核心筒两个方向的损伤相互耦合，加速了筒体墙肢裂缝的出现和发展，且较之单向加载的情况有明显的扭转效应，筒体达到最大承载力后，很快达到极限承载力，延性较差。

表3 不同加载方式时核心筒特征量对比 Table 3 Characteristic values of specimen with different load modes

注：y、d、u分别代表屈服荷载、极值荷载和极限荷载；u、d、y分别代表达到各特征荷载时所对应的位移。

2 参数分析

为进一步明确核心筒在双向水平荷载作用下的空间受力性能，讨论轴压比、连梁跨高比和截面长宽比等因素的影响，各模型均采用双向水平矩形加载。

2.1 轴压比

对轴压比（）分别取0.15、0.24、0.45、0.60及0.80的核心筒进行非线性分析，轴压比采用试验轴压比，由各模型损伤分布和开展可知，轴压比较小时，如=0.15的核心筒在其底部受拉纵筋屈服后，受压区混凝土压碎，筒体达到极限承载力，为弯曲破坏；当轴压比增大，如达到0.60及以上时，筒体底部受压区混凝土突然压碎，发生脆性破坏。

核心筒顶部位移-基底剪力曲线如图8所示，各模型特征量如表4所示。可知，随着轴压比的增大，各特征荷载均先增大后减小，在=0.45时达到最大值，如向最大承载力比=0.15时增大了15.0%，当=0.60时，向承载力已比最大值降低了15.2%，当=0.80时，则降低了39.1%。而单向荷载作用下轴压比取0.60时承载力达到最大，此时筒体仍为弯曲破坏（周忠发等，2010），可见，较大的轴压比将使筒体发生剪切破坏，延性降低，对于双向加载的情况更加不利。取刚度退化系数为/0，其中0为弹性阶段的初始刚度值，为割线刚度，则各模型刚度退化曲线如图9所示。可见，轴压比较小的时候，初期刚度退化较快，筒体屈服后刚度退化逐渐减慢，达到最大荷载后则趋于平缓；当轴压比大于0.45之后，模型刚度迅速下降，筒体延性较差。可以认为，筒体双向受力不均匀的情况对于轴压比的限制更为严格，工程设计上应引起注意。

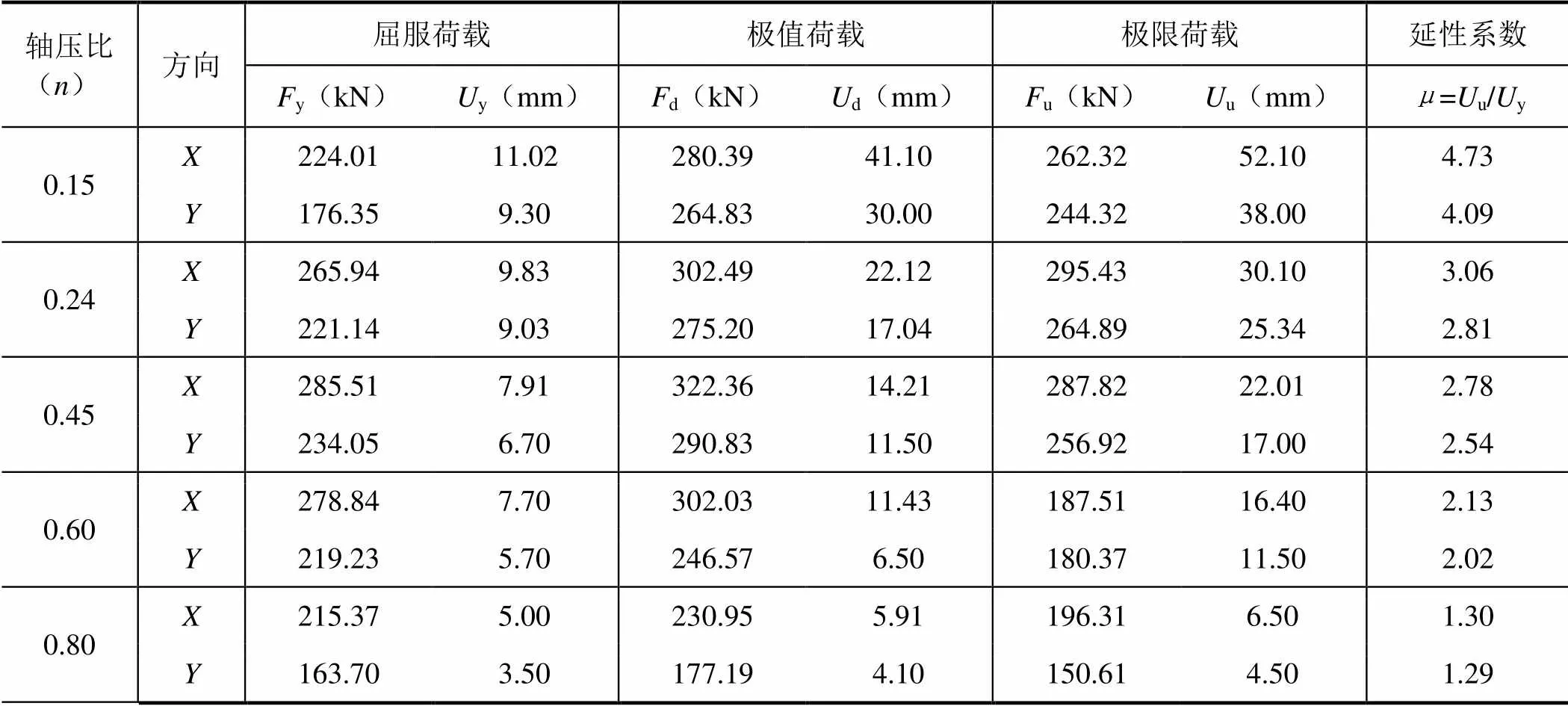
表4 不同轴压比下核心筒特征量对比 Table 4 Characteristic values of specimen with different axial compression ratio

2.2 连梁跨高比

对连梁跨高比（）分别为0.72、1.62和2.48的核心筒进行分析，其洞口尺寸分别为150mm×260mm、340mm×260mm、520mm×260mm。由各模型损伤分布和开展可知，随着连梁跨高比的增大，模型的破坏形式由连梁对角斜裂缝贯通的剪切破坏向梁端弯曲破坏转化。

图10为核心筒顶部位移-基底剪力曲线，各模型特征量如表5所示。可见，随着连梁跨高比的增大，屈服荷载和极值荷载均明显减小，其中极值荷载降低了43.6%，相应的屈服位移和极值位移略有增大，延性系数提高了34.6%。在单向荷载作用下，当连梁跨高比从0.4增大到2.4时，极值荷载降低了36.7%，当连梁跨高比从0.9增大到2.4时，延性系数提高了58.3%（赵均等，2010），显然，连梁跨高比的改变对于空间受力状态下的核心筒影响更大。由图11所示的刚度退化曲线可知，连梁跨高比越大，刚度退化曲线越缓和。可见，洞口大小的改变直接改变了单片墙肢的高宽比和连梁的跨高比，破坏机制将会随之发生改变，合理确定核心筒连梁跨高比对改善核心筒的抗震性能提高其延性非常重要。

（a）向        （b）向

图10 不同连梁跨高比的核心筒顶部位移-基底剪力曲线
Fig.10 Base shear-top displacement vs. high aspect ratio of coupling beam

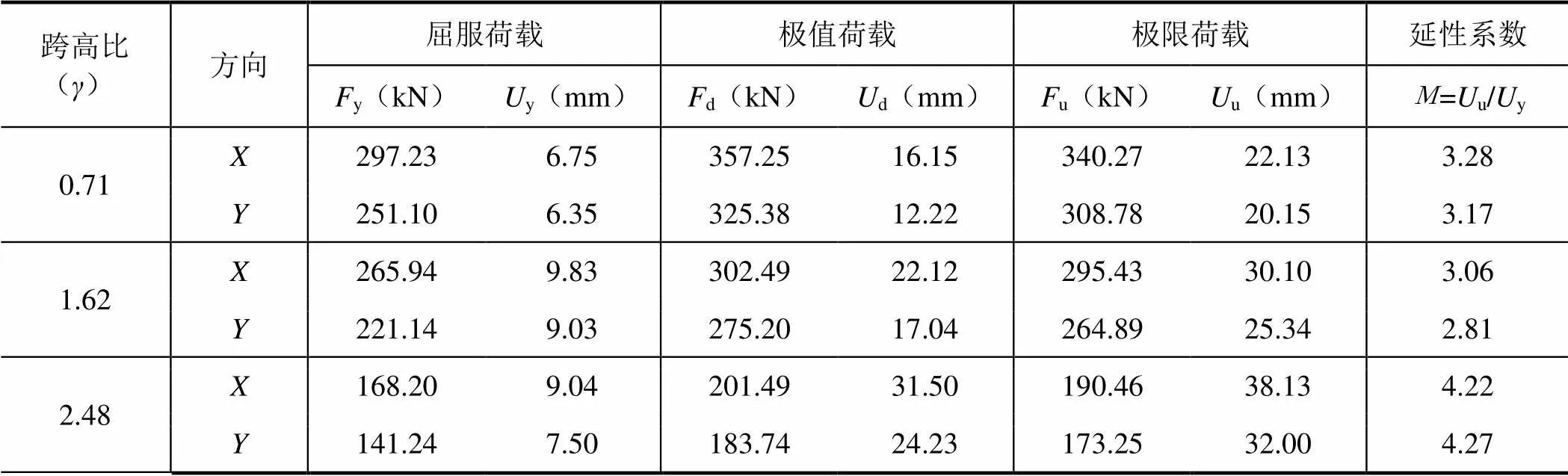
表5 不同连梁跨高比的核心筒特征量对比 Table 5 Characteristic values of specimen with different high aspect ratio of coupling beam

（a）向        （b）向

图11 不同连梁跨高比的核心筒刚度退化曲线
Fig. 11 Stiffness degradation curves of specimen with different high aspect ratio of coupling beam

2.3 截面长宽比

为研究两个方向刚度差异对核心筒受力性能的影响，对筒体截面长宽比（/）分别为1.00、1.50和1.78的模型进行分析，其平面尺寸分别为1050mm×1050mm、900mm×1350mm、900mm×1600mm，向为强轴方向。由各模型损伤分布和开展可知，随着长宽比的增大，核心筒两个方向的刚度差异不断增大，模型破坏的位置发生改变，由于强轴方向二层处剪切裂缝与弯曲裂缝的相互交织，最后破坏主要发生于强轴二层与弱轴的一层，强轴方向墙肢剪切破坏严重，裂缝开展不充分，耗能较弱。在/=1.78的模型中，发生底部严重破坏的同时，在强轴方向第七层处连梁出现严重损伤。

图12为不同截面长宽比的核心筒顶部位移-基底剪力曲线，表6为对应的核心筒特征量。可见，随着长宽比的增大，强轴方向上的屈服荷载和极值荷载不断增大，对应的屈服位移和极值位移则不断减小，延性降低；弱轴方向表现则相反，刚度差异大的模型承载力更低，但总体变化不明显。如图13所示的刚度退化曲线表示，随着长宽比的增大，即刚度差异的加大，刚度衰减速度加快，强轴方向表现更加明显。

（a）向          （b）向

图12 不同截面长宽比的核心筒顶部位移-基底剪力曲线
Fig. 12 Base shear-top displacement curves of specimen with different length-width ratio of the section

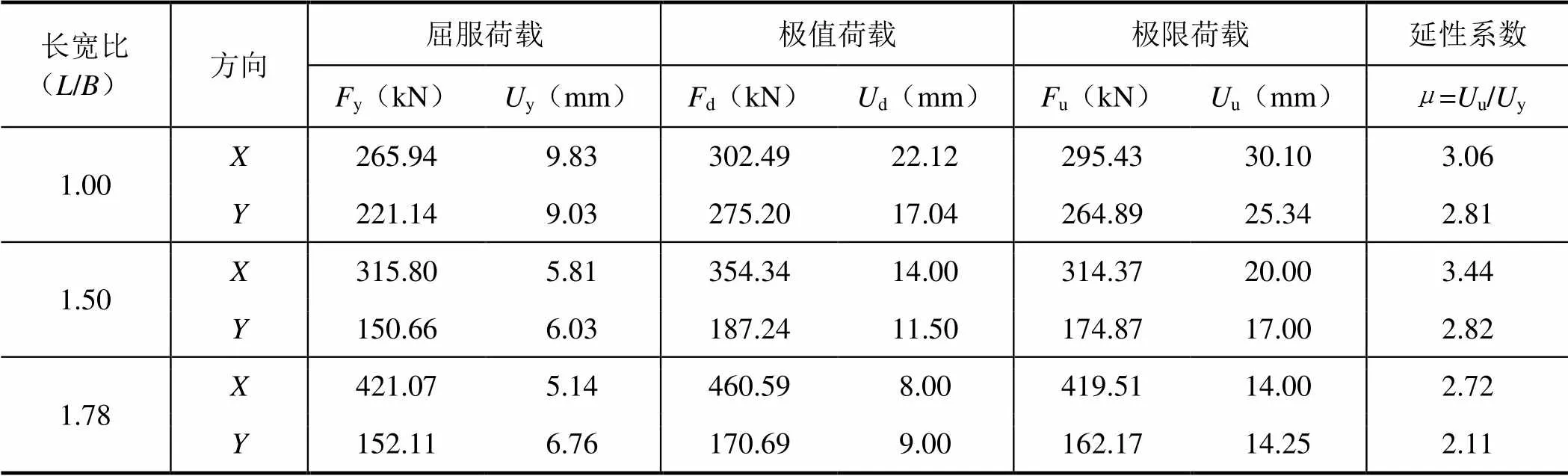
表6 不同截面长宽比的核心筒特征量对比 Table 6 Characteristic values of specimen with different length-width ratio of the section

（a）向          （b）向

图13 不同截面长宽比的核心筒刚度退化曲线
Fig. 13 Stiffness degradation curves of specimen with different length-width ratio of the section

因此，两个方向刚度的差异对核心筒的延性有较大的影响，刚度差异加大使核心筒承载力下降变快，导致后期承载力不足。《高层建筑混凝土结构技术规程》（JGJ 3-2010）第9.2.6条规定，当内筒长宽比大于2时，宜采用框架-双筒结构。可以认为，当考虑双向荷载作用下的空间效应时，该长宽比限制可更加严格，并且应进行局部构造加强。

3 双向水平荷载作用下混凝土核心筒承载力计算

由以上分析可知，双向水平荷载作用下混凝土核心筒承受压力、剪力、弯矩和扭矩的复合作用，在混凝土开裂后，这样的压、弯、剪、扭复合受力构件是一个带裂缝工作的空间受力问题，受力情况非常复杂。常卫华（2008）对模型骨架曲线中核心筒承载力的计算公式进行了研究，但并未考虑混凝土核心筒开洞以及混凝土强度的影响，而连梁跨高比是影响核心筒抗震性能的重要因素。

本文采用空间桁架理论（Rausch，1929；Thürlimann，1997）对复合受扭构件的承载力进行计算，进一步考虑了加载方式、洞口大小以及混凝土强度对承载力的影响，得到的核心筒承载力计算公式如式（1）所示，其中，、、、分别为核心筒所受弯矩、扭矩、剪力和轴压力。

（，，）为考虑加载方式、洞口大小以及混凝土强度的综合影响系数，按式（2）计算。

（）=··（2）

其中，为考虑加载方式的影响系数，双向水平加载的情况下取值为0.9，单向加载时则取1.0；为核心筒洞口大小影响系数，由式（3）求得；为核心筒混凝土强度的影响系数，由式（4）可得。

=0.588+0.0242+0.237+3.296+1.991（3）

=0.0002c2-0.0067c+1.0192 （4）

式中，为核心筒的连梁跨高比；为核心筒的腹板开洞率；c为混凝土的轴心抗压强度。

为验证公式的适用性与可靠性，笔者采用式（1）得到的核心筒承载力计算结果与本项目试验及文献结果进行了比较，如表7所示。其中，对于仅受双向水平荷载的筒体，其扭矩近似用所受水平推力和与之垂直方向上的位移乘积表示。可见，利用本文计算公式所得的核心筒承载力均比试验值略大，但最大增幅不到10%。考虑到实际设计中应对核心筒各关键部位进行加强，而试验中均为未加强的状态，可认为本文给出的公式是适用的。

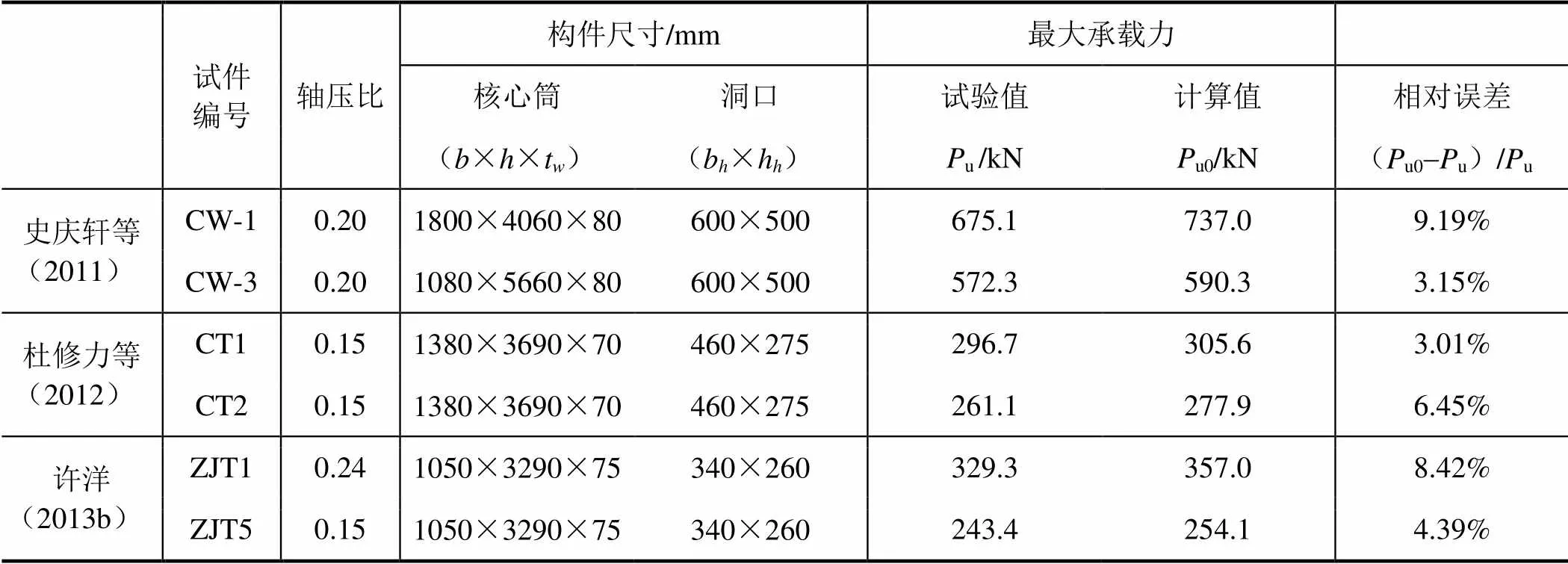
表7 核心筒承载力对比 Table 7 Comparison between theoretical and experimental flexural capacity

注：u、u0分别代表承载力的试验值和计算值；t为核心筒的壁厚；bh分别为洞口的宽度和高度。

4 结论

本文运用ABAQUS软件对双向水平往复荷载作用下的钢筋混凝土核心筒进行非线性有限元分析，研究了轴压比、连梁跨高比和截面长宽比等因素对核心筒破坏特征、承载力、刚度退化及耗能能力的影响，得到的主要结论如下：

（1）与单向水平荷载作用相比，双向水平荷载作用下筒体的破坏形态没有显著变化，均为底部钢筋受拉屈服后混凝土压溃的整体弯曲破坏。但两个方向的损伤相互影响导致了筒体的刚度退化加剧，变形能力降低，扭转效应显著增大，使得筒体最大承载力减小，抗震性能明显降低。

（2）轴压比是控制核心筒破坏状态的重要因素，当轴压比大于0.45后，筒体的破坏形态将由延性破坏变为脆性破坏，刚度退化加剧；两个方向刚度差异较大的筒体变形能力以及延性均有较大的降低，在设计中应注意平面布置对筒体空间受力性能的影响。随着连梁跨高比的增大，连梁的破坏形态由剪切破坏向弯曲破坏转变，筒体转动能力提高，耗能能力增强，工程设计中应合理控制连梁跨高比，确保连梁纵向钢筋屈服先于截面剪切破坏。

（3）采用空间桁架理论，考虑加载方式、筒体洞口大小以及混凝土强度对核心筒承载力的影响，得到了压弯剪扭复合作用下核心筒的承载力近似计算公式，并与试验结果符合较好。

常卫华，2008．内藏钢桁架混凝土组合核心筒抗震试验及理论研究．北京：北京工业大学建筑工程学院．

杜修力，贾鹏，赵均，2012．水平双向加载条件下钢筋混凝土核心筒抗震性能试验研究．建筑结构学报，33 （10）：7—12．

方鄂华，钱稼茹，1999．我国高层建筑抗震设计的若干问题．土木工程学报，32（1）：3—8．

侯炜，史庆轩，郭子雄，2013．不同参数钢筋混凝土核心筒抗震性能研究．工程力学，30（10）：77—85．

史庆轩，侯炜，刘飞，郭栋，张兴虎，2011．钢筋混凝土核心筒抗震性能试验研究．建筑结构学报，32（10）：119—129．

徐培福，傅学怡，王翠坤，肖从真，2005．复杂高层建筑结构设计．北京：中国建筑工业出版社．

许洋，赵均，徐金蓓，李月，侯鹏程，2013a．混凝土核心筒的水平双向循环加载试验研究．震灾防御技术，8 (2)：173—180．

许洋，2013b．水平双向循环加载下混凝土核心筒性能的试验研究．北京：北京工业大学建筑工程学院．

赵均，马家幸，贾鹏，杜修力，2006．混凝土核心筒反复加载性能的试验研究．建筑结构，36（增刊1）：41—44．

赵均，周忠发，2010．混凝土核心筒水平受力性能的非线性有限元分析．土木工程学报，43（增刊）： 150—157．

周忠发，赵均，2010．混凝土核心筒的有限元模拟及若干参数的影响分析．防灾减灾工程学报，30 (6)： 660—666.

Atsushi Habasaki, Yoshio Kitada, Takao Nishikawa et al., 2000. Multi-directional loading test for RC seismic shear walls．12WCEE，Paper No. 454．

Thürlimann B., 1979. Torsional Strength of Reinforced and Prestressed Concrete Beam-CEB Approach. Concrete Design: US and European Pacfices, SP-59: 117-143．

Rausch E., 1929. Design of Reinforced Concrete in Torsion. Berlin:Technische Horchschule．

Nakachi T., Toda T. et al., 1996．Experimental study on deformation capacity of reinforced concrete core walls after flexural yielding. 11WCEE, Paper No.1747．

Analysis on the Performance of Reinforced Concrete Core Walls under Biaxial Cyclic Lateral Loading

Chen Ying1, 2), Liu Zhao1)and Zhao Jun1, 2)

1) College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China 2) Key Lab of Urban Security& Disaster Engineering MOE, Beijing University of Technology, Beijing 100124, China

Seismic performance of reinforced concrete core wall under biaxial cyclic lateral loading is studied by finite element (FE) analysis. A FE model is built by software ABAQUS to carry out nonlinear analysis. The model is then verified by comparing its computational results with results of corresponding large-scale specimen model tests. Compared to the case of the tests under uniaxial cyclic loadings, the biaxial loadings effects result in significant decrease in bearing capacity and deformation ability, and a faster degradations in stiffness, which obviously reduces the seismic performance．Then, reinforced concrete core walls under biaxial cyclic lateral loadings with different parameters are simulated by elasto-plastic finite element analysis. Influences of the seismic behavior of reinforced concrete core wall are studied, including axial compression ratio, span-height ratio of coupling beam and length-width ratio of the section and so on. Compare these results with that under single direction loading, it is found that axial compression ratio and span-height ratio of coupling beams are all key factors influencing the failure mode of the core wall. And the differences of stiffness in two directions result in the dropping in capacity of deformation and ductility. Further, considering the spatial effect of torsion and influences of loading mode, opening size and concrete strength, a calculation formulae for bearing capacity of the reinforced concrete core wall under combined action of bending, shear and torsion is proposed. The results are in good accordance with that from tests.

Core walls; High-rise building; Biaxial cyclic lateral loading; Seismic performance

[1] 基金项目 国家自然科学基金青年基金（51108008）

［收稿日期］ 2015-04-03

［作者简介］ 陈盈，女，生于1981年。博士，讲师，硕士研究生导师。主要从事多高层结构抗震研究。E-mail：chenying@bjut.edu.cn

陈盈，刘昭，赵均，2016．钢筋混凝土核心筒水平双向抗震性能研究．震灾防御技术，11（1）：55—66．

doi：10.11899/zzfy20160106