郑州市的交通拥堵治理及雾霾治理的协调问题

胡康静　魏子钰

摘 要：随着经济的发展，郑州的机动车数量与日俱增，导致交通日渐拥堵，与此同时空气质量指数却每况愈下，本文是针对郑州市交通拥堵现状和雾霾进行分析，从而找到两者的相关性，最后科学的提出如何有效的治理交通拥堵以及雾霾问题。

关键字：灰色模拟系统；相关性 minitab软件；线性规划 matlab软件

1 解决的问题

用数学建模的方法解决交通拥堵以及空气质量的治理问题并进行以下分析：

（1）在现有不变的模式下，进行对2015-2025年郑州市交通拥堵和空气质量的发展趋势预测。

2 模型的建立及求解

2.1 对问题的分析

在问题（1）中，交通拥堵的状况用通过平均每新建一公里道路增长车辆数来表示。其次空气质量变化趋势则用空气质量指数（AQI）的变化来表示。

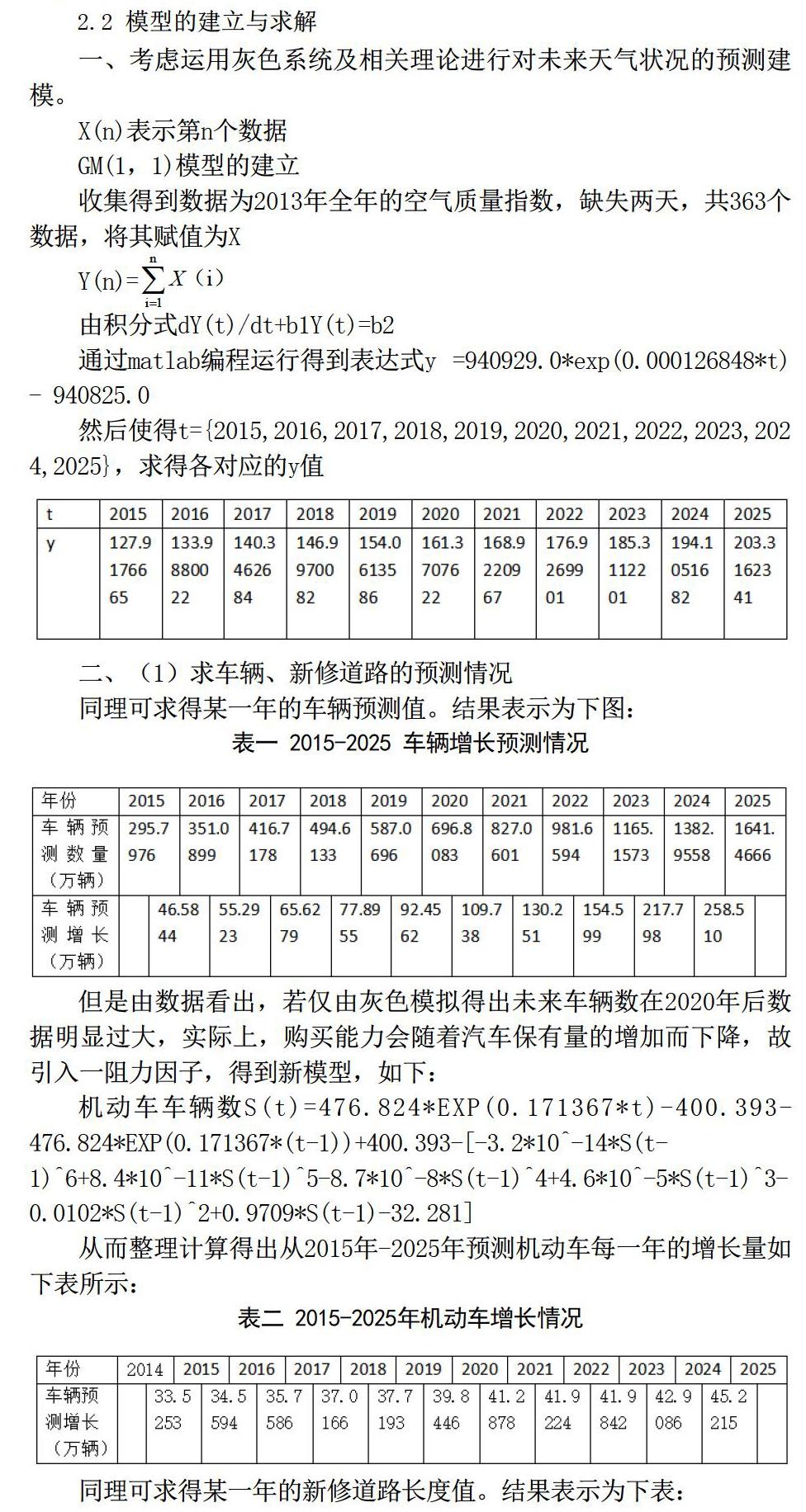
2.2 模型的建立与求解

一、考虑运用灰色系统及相关理论进行对未来天气状况的预测建模。

X（n）表示第n个数据

GM（1，1）模型的建立

收集得到数据为2013年全年的空气质量指数，缺失两天，共363个数据，将其赋值为X

由积分式dY（t）/dt+b1Y（t）=b2

通过matlab编程运行得到表达式y =940929.0*exp（0.000126848*t） - 940825.0

然后使得t={2015，2016，2017，2018，2019，2020，2021，2022，2023，2024，2025}，求得各對应的y值

二、（1）求车辆、新修道路的预测情况

同理可求得某一年的车辆预测值。结果表示为下图：

但是由数据看出，若仅由灰色模拟得出未来车辆数在2020年后数据明显过大，实际上，购买能力会随着汽车保有量的增加而下降，故引入一阻力因子，得到新模型，如下：

机动车车辆数S（t）=476.824*EXP（0.171367*t）-400.393-476.824*EXP（0.171367*（t-1））+400.393-[-3.2*10^-14*S（t-1）^6+8.4*10^-11*S（t-1）^5-8.7*10^-8*S（t-1）^4+4.6*10^-5*S（t-1）^3-0.0102*S（t-1）^2+0.9709*S（t-1）-32.281]

从而整理计算得出从2015年-2025年预测机动车每一年的增长量如下表所示：

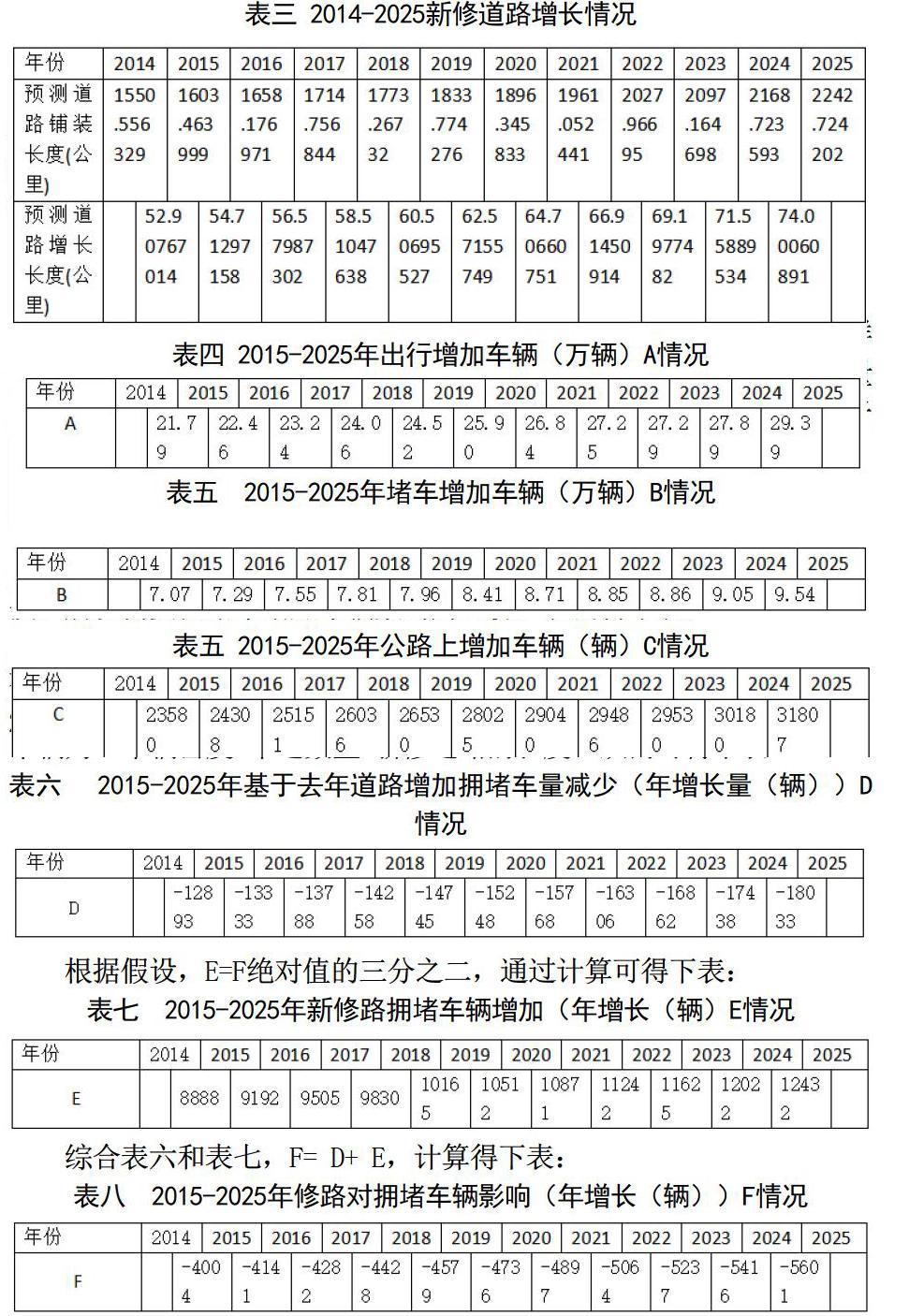
同理可求得某一年的新修道路长度值。结果表示为下表：

（2）增加车辆对交通拥堵的影响

查得郑州市车辆保有量和上路量之间关系为40～50%，考虑到新车上路机会多，且一车一天可多次出行，以及其他因素的影响等，则最终取得65%的比例关系，得下表：

出行车辆数并不能代表拥堵车辆，因此选取了八个路口作为样本，某一路口的拥堵车辆数占出行车辆的比例数=（高峰期的车流量数—平峰期的车流量数）/高峰期的车流量数，取平均比例数等于0.324625，用每年出行增加车辆数*0.324625得到下表：

在实际情况中，一天的车辆拥堵高峰期分为早、中、晚三个时间段，所以需要把堵车增加车辆数均为三份，从而得下表：

（3）新修道路对交通拥堵的影响（—：拥堵车量减少，+：拥堵车辆数增加）

理想条件下，由多车道不控制出入一级公路服务水平分级指标，有最大车辆密度（veh/km/ln）<=42，最大服务流率（veh/h/ln）为2000。郑州的道路车道为六车道。所以基于去年新修道路缓解拥堵的车辆为：车辆密度*车道数量*新修道路的长度。从而可得下表：

根据假设，E=F绝对值的三分之二，通过计算可得下表：

综合表六和表七，F= D+ E，计算得下表：

（4）修路和公路上增加车辆对拥堵车辆的影响

结合表五和表八，得出修路和公路上增加车辆对拥堵车辆的影响 = 公路上增加车辆+ 修路对拥堵车辆影响，得下表：

3 结果的表示

（1）对于2015-2025年空气质量的变化趋势的回答如下：

最终整合求得的y、t数据绘制曲线图如下：

由上图可得在未来十年里，空气质量指数逐渐上升，且上升速度有增加的势头。

对于2015-2025年交通拥堵的发展状况的回答如下：

将表九的数据绘制成折线图如下：

通过上图可得出结论在未来十年交通的发展状况将会愈渐拥堵。

参考文献

[1] 韩中庚，数学建模方法及其应用[M]，北京：高等教育出版社，2005

[2] 盛骤，谢式千，概率论与数理统计，北京：高等教育出版社，2003

[3] 费业泰，误差理论与数据处理（第五版），北京：机械工业出版社，2004.6

[4] 韩中庚，数学建模方法及其应用，北京：高等教育出版社，2005.6