EHF频段芯片引线键合与装配公差的仿真与分析
卢绍英,任 榕
(中国电子科技集团公司 第三十八研究所,安徽 合肥 230000)
EHF频段芯片引线键合与装配公差的仿真与分析
卢绍英,任榕
(中国电子科技集团公司 第三十八研究所,安徽合肥230000)
文章从工程角度出发,使用仿真软件分别对极高频(Extremely High Frequency,EHF)频段芯片的引线键合和装配公差进行了仿真分析,确定键合线的拱高、距离等参数,明确装配公差的合理范围,以便减小芯片级联时的射频损耗,并满足多个射频模块之间的一致性要求。
EHF频段;键合线;装配公差
近年来国内EH F频段技术发展迅速,其频段为30~300GHz,宽带宽、容量高、截获概率低、抗干扰能力强,在卫星通信技术中前景广阔[1],其设备的需求日益迫切。EHF频段频率高,分布参数影响大,加工、制造工艺复杂,对芯片的匹配设计和装配的工艺控制提出了很高的要求。
本文旨在通过对芯片引线键合与装配公差的仿真与分析,确定键合线的参数与装配公差带来的影响,为EHF频段射频模块设计提供依据。软件采用三维电磁场分析软件高频结构仿真(High Frequency Structure Simulator,HFSS),建立了仿真模型并进行分析和优化,仿真结果直接指导EHF频段射频模块的设计、加工和装配,最终EHF频段射频模块性能满足指标。
1 仿真模型
HFSS采用有限元法,能计算任意形状三维无源结构的S参数和全波电磁场。其自带键合线模型,对分析键合引线参数十分便利。
仿真模型中,选择砷化镓作为微带线介质模拟芯片键合焊盘,介电常数12.9,微带线宽度0.2mm。过渡微带线选择高频板RT6002, 厚度0.254mm,微带线宽度0.66mm。过渡微带考虑激光切割配装,故端口未作展宽处理。
2 键合线的仿真与分析
通常射频电路中键合线采用压焊工艺,键合线形状如图1所示,实际操作过程中可以对键合线的键合位置和拱高进行控制。故本文使用HFSS软件自带JEDEC4-point Bondwires模型(见图2)近似仿真,其参数如下:

分别设置金丝的直径(Diameter)、距离(D)和拱高(h1)为变量进行仿真分析。键合线参数仿真时不考虑装配工差的影响。

图1 压焊键合线照片

图2 JEDEC-4 Bondwires模型
2.1单根键合金丝的仿真
单根键合金丝的仿真模型如图3所示,芯片与微带板缝隙宽度为25μm,无高度差。

图3 单根键合金丝模型
2.1.1直径对驻波的影响
常规金丝直径有12.7μm,25μm和38μm。设置金丝距离0.5mm,拱高0.1mm,其余参数不变的情况下,通过仿真得出:直径越大,驻波越好。仿真结果如图4所示。

图4 单根金丝直径变化的仿真结果
2.1.2距离对驻波的影响
设置金丝直径25μm,拱高0.1mm,余参数不变的情况下,通过仿真得出:距离越小,驻波越好。仿真结果如图5所示。

图5 单根金丝距离变化的仿真结果
2.1.3拱高对驻波的影响
设置金丝直径25μm,距离0.5mm,余参数不变的情况下,通过仿真得出:拱高越小,驻波越好。仿真结果如图6所示。

图6 单根金丝拱高变化的仿真结果
2.2两根键合金丝的仿真
两根键合金丝的仿真模型如图7所示,芯片与微带板缝隙宽度为25μm,无高度差。
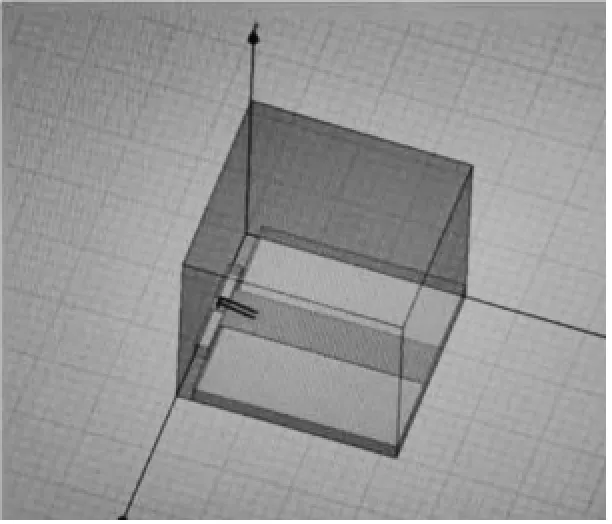
图7 两个键合金丝模型
2.2.1直径对驻波的影响
设置金丝距离0.5mm,拱高0.1mm,其余参数不变的情况下,通过仿真得出:直径越大,驻波越好。仿真结果见图8。

图8 两根金丝直径变化的仿真结果
2.2.2距离对驻波的影响
设置金丝直径25μm,拱高0.1mm,余参数不变的情况下,通过仿真得出:距离越小,驻波越好。仿真结果如图9所示。
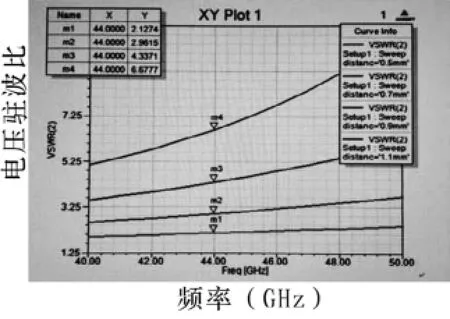
图9 两根金丝距离变化的仿真结果
2.2.3拱高对驻波的影响
设置金丝直径25μm,距离0.5mm,余参数不变的情况下,通过仿真得出:拱高越小,驻波越好。仿真结果如图10所示。

图10 两根金丝拱高变化的仿真结果
2.2.4角度对驻波的影响
对键合线的键合位置控制,可以使两根键合线形成一定的夹角(见图11),设置金丝直径25μm,距离0.5mm,拱高0.1mm,余参数不变的情况下,通过仿真得出:角度增加对驻波有改善,但改善较小。仿真结果如图12所示。

图11 两根金丝形成一定的角度

图12 两根金丝角度改变对驻波的影响
2.3键合金丝的参数控制
通过仿真结果可知,在同等参数下,两根金丝性能优于单根金丝,金丝直径越大、距离越短、拱高越低,驻波越小,角度的增加对驻波有改善,但影响较小,拱高改变对驻波的影响最大。
鉴于芯片焊盘尺寸的大小和压焊工艺的特点,推荐采用两根金丝,且尽量使用机器操作控制精度,避免人为误差。
3 装配公差的仿真与分析
通过模拟芯片与微带板高度差和缝隙间隔的大小,分析对驻波的影响。仿真模型如图13所示。
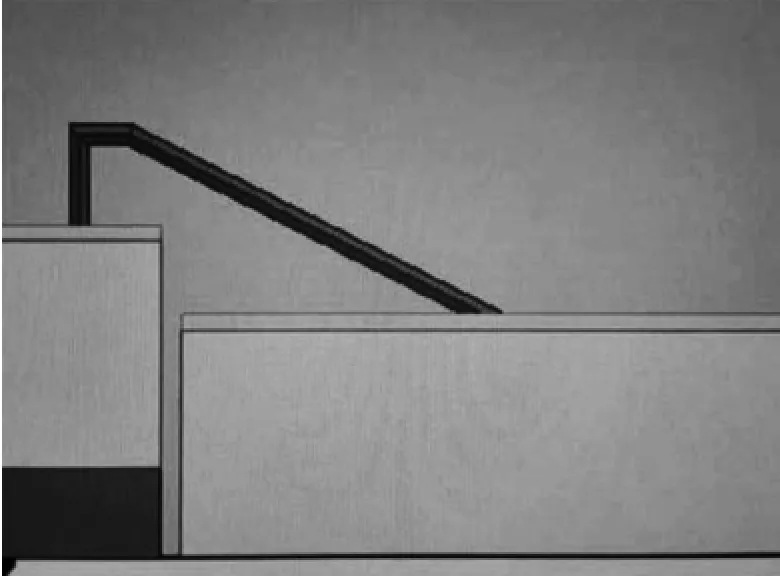
图13 装配公差仿真模型
3.1高度差对驻波的影响
设置金丝直径25μm,距离0.5mm,拱高0.1mm,芯片与微带板缝隙间隔25μm,余参数不变的情况下,通过仿真得出:高度差越大,驻波越差。仿真结果如图14所示。

图14 高度差对驻波的影响
3.2缝隙间隔对驻波的影响
设置金丝直径25μm,距离0.5mm,拱高0.1mm,无高度差,余参数不变的情况下,通过仿真得出:无缝隙间隔时,驻波值最好;有缝隙间隔时,驻波恶化。仿真结果如图15所示。

图15 缝隙间隔对驻波的影响
3.3装配公差的控制
通过仿真结果可知,在EHF频段下,装配公差对驻波影响较大,高度差越小,驻波越好;缝隙宽度对驻波的影响更大,当无缝隙时,驻波极。工艺控制时应尽量减小公差,并兼顾组建的一致性要求。
4 结语
本文对引线键合的参数与装配公差的控制进行了仿真分析,此种方法更贴近实际工程,可以对EHF频段射频模块的设计、加工和装配进行指导。通过仿真发现改变键合线的参数,可以改变端口的驻波特性,故此方法也可以成为模块调试的手段。
[1]袁飞,文志信,王松松.美军EHF卫星通信系统[J].国防科技,2010(31):22.
Simulation and analysis of EHF band chip wire bonding and assembly tolerance
Lu Shaoying, Ren Rong
(The Thirty-eighth Institute of China Electronic Technology Group Corporation, Hefei 230000, China)
This paper conducts simulation analysis on EHF band chip bonding and assembly tolerances by using simulation software from the view of the engineering, then determines the parameter of bonding wire such as arch height and distance, clears the reasonable range of assembly tolerance in order to reduce RF loss in the chip cascade and meet the consistent requirements among multiple radio frequency modules.
EHF band; bond line; assembly tolerance
卢绍英(1983— ),男,吉林吉林,硕士;研究方向:射频收发通道/模块。

