单相交流电子负载电感参数的选取分析

江秀浩，党幼云，王湘涛，韩明琦，涂　展

（西安工程大学 电子信息学院，陕西 西安 710048）

单相交流电子负载电感参数的选取分析

江秀浩，党幼云，王湘涛，韩明琦，涂展

（西安工程大学 电子信息学院，陕西 西安 710048）

文章对电路拓扑结构为电压型PWM的整流器采用滞环电流控制的单相交流电子负载，目前其交流侧电感参数的选取缺乏相关理论基础。文中先对快速跟踪给定电流进行单独分析，得出电感参数选取范围的上限；再对器件的开关频率限制和抑制谐波电流进行综合分析比较，得出电感参数选取范围的下限，最终确定出交流侧电感参数的选取范围。最后通过在Matlab/Simulink中进行仿真实验，验证了该电感选取方案的可行性，具有一定的实用性。

PWM整流器；电子负载；电感参数

交流电子负载通过控制电力电子器件，能够模拟阻感、阻容、纯电阻等不同的负载，实现四象限运行。交流侧电感参数的选取很重要，其取值不仅对输出电流质量有直接的影响，而且对系统的响应速度、直流电压纹波水平也有影响。电感取值过大虽然有助于谐波电流的抑制，但却减慢系统的响应速度；电感取值过小虽然能够达到快速跟踪电流的能力，但却使电感电流谐波很大。因为交流电子负载采用滞环PWM电流控制，所以开关器件的频率也不固定，这也对电感值的选取有了一定的限制。文献［1］考虑了快速跟踪给定电流、抑制谐波和开关频率限制，但在分析快速跟踪给定电流上用了极限近似值法，不能分析出任意负载情况，存在一定的缺陷；文献［2］在分析抑制谐波电流时将器件的开关周期当作已知量，而实际上器件的开关周期为变量，同样存在缺陷。此外，在查阅文献过程中发现，大多数文献在分析开关频率限制和抑制谐波电流时只是对它们进行独立分析，并没有将两者相结合分析。本文在分析快速跟踪给定电流中，通过建立任意负载时刻电感参数的数学模型来确定电感值选取范围的上限；通过对器件的开关频率限制和抑制谐波电流进行综合分析比较得出电感值选取范围的下限，最终确定出电感参数的选取范围。最后通过仿真实验对结论进行了验证。

1　单相交流电子负载拓扑结构

如图1所示，单相交流电子负载的拓扑结构基础是电压型PWM整流器（Voltage Source Rectifer，VSR）。其中L为等值电感，可作为临时储能元件传递能量，也可抑制高次谐波电流；VT1—VT4是全控型开关器件；电容C为直流侧母线稳压电容，起稳压和滤波作用。直流母线电压UDC必须大于交流电源电压峰值，PWM整流器才能正常工作［3—4］。

本文采用响应速度快、鲁棒性好的滞环控制方式［4—5］。滞环控制的优点是硬件电路简单、电流响应速度快和不需要载波等。其控制方式为：用测得的实际电流与给定电流做差，其差值作为滞环比较器的输入信号；用滞环比较器的输出信号来控制开关器件的通断，从而使实际电流跟随给定电流，模拟任意负载。

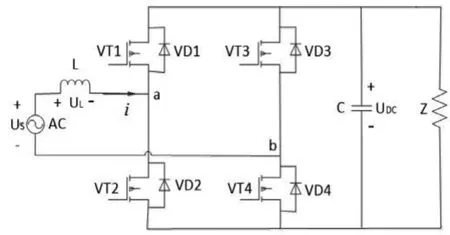
图1　单相交流电子负载主电路拓扑结构

2　电感参数L的选取

本文主要分析双极性滞环控制下电感参数的选取。

2.1快速跟踪给定电流

单相交流电子负载交流侧矢量图如图2所示。其中A，B，C，D分别表示系统工作于纯电感、纯电阻、纯电容和恒负阻状态，A∧B，B∧C，C∧D，D∧A分别表示系统工作于阻感、阻容、能馈阻容和能馈阻感状态。

图2　单相交流电子负载交流侧矢量图

根据余弦定理，有

可解得：

式中：φ表示系统功率因数角，Usm表示交流电源电压峰值，Im表示交流侧基波电流峰值，Uabm表示交流侧基波电压峰值。

又Uabm=MUDC（4）

式中：M表示PWM相电压最大利用率［6］。

将式（4）代入式（3）中得到：

由图2知，若系统工作于阻感状态，有0≤θ≤90°和0≤φ≤90°；系统工作于阻容状态时，有90°≤θ≤180°和0≤φ≤-90°；系统工作于能馈状态D点时，有θ=270°和φ= -180°。

根据以上分析可知，当系统模拟线性负载时，只有系统工作于C点，即纯电容状态，电感值的上限才取最小值，此时应满足：

当系统处在能量回馈单元，即工作于恒负阻时，其理想状况下应该工作于D点，此时电感应满足：

综上：当系统模拟线性负载时，用公式（6）来确定电感参数选取范围的上限；当系统模拟恒负阻时，用公式（7）来确定电感参数选取范围的上限。

2.2器件的开关频率限制和抑制谐波电流

在选取电感参数时，还要考虑到器件的开关频率限制和抑制谐波电流。滞环控制电流波形如图3所示。图中i*为给定电流，i为实际电流，Iω为滞环宽度。

图3　滞环控制电流波形

2.2.1器件的开关频率限制

由于器件的开关频率远大于给定电流的频率，因此在一个开关周期内，给定电流值可近似看成不变［7］。若不考虑直流电压的波动，即直流电压维持在UDC。

当0≤t≤t1时，VT2（VD2）、VT3（VD3）导通，电流i从i*0.5Iω上升到i*+0.5Iω，电流变化量为Iω，有：

当t1≤t≤t2时，VT1（VD1）、VT4（VD4）导通，电流i从i*+0.5Iω下降到i*-0.5Iω，电流变化量为-Iω，

有：器件的开关周期：

由式（8）、式（9）、式（10）可得：

则器件的开关频率为：

由于Us=Usmsin（ωt）是一个变量，所以器件的开关频率f不是一个定值。器件的开关频率最大值为：

设所采用的开关器件的最高频率为F，则fmax≤F，得到：

2.2.2抑制谐波电流

电感具有抑制谐波电流的作用。在正弦波电流峰值附近，电流脉动幅度最大，此处电感值应足够大［8］。

由式（11）得：

式中：Iω为电流变化量。

根据抑制峰值电流谐波的要求，若谐波电流允许的最大脉动幅值为△Imax，则电感L的取值应大于式（15）右端最大值。由2.2.1对器件的开关频率限制分析知，器件的开关周期T 不是一个定值。当Us=0时，UDC2-Us2最大，有：

综上：由式（14）和式（17）知，电感参数选取范围的下限应由式（14）确定，考虑到抑制谐波电流，电感L的取值应尽量大。

2.3电感的选取

电感参数L的选取应综合考虑以上3方面因素。当系统模拟线性负荷时，取式（6）、式（14）的交集得出电感L的选取范围；当系统模拟恒负阻时，取式（7）、式（14）的交集得出电感的选取范围，且电感L的取值应尽量大。

3　仿真实验

在Matlab/SimulinK环境中搭建仿真实验平台。本实验中设定输入交流电源电压有效值为115V，频率为200Hz，直流母线电压为400V，输入电流最大值Im=25A，器件的开关频率为20KHz，滞环宽度Iω=2A。当系统模拟线性负荷时，取式（6）和式（14）的交集，得到电感L的选取范围：5mH≤L≤7.6mH；当系统模拟恒负阻时，取式（7）和式（14）的交集，得出电感L的选取范围：5mH≤L≤11.6mH。实验以模拟阻容性负载Z=5-j5Ω和恒负阻Z=-6.5Ω为例，L分别取1mH，7mH，10mH和2mH，10mH，15mH得出各自电感电流的仿真波形，如图4—9所示。

图4　电感L=1mH时的电流波形

图5　电感L=7mH时的电流波形

图6　电感L=10mH时的电流波形

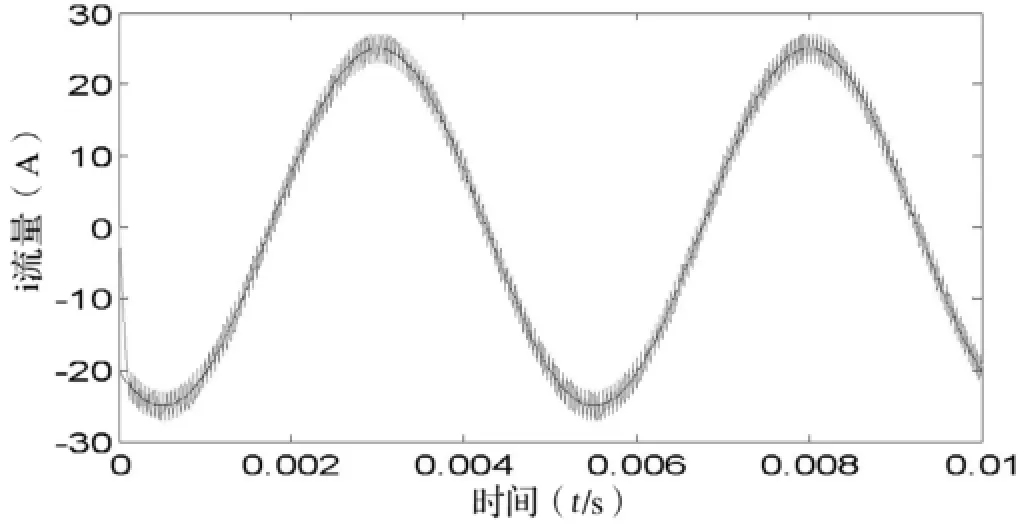
图7　电感L=2mH时的电流波形

图8　电感L=10mH时的电流波形

从以上图中可知：当电感L取值比规定范围小时，电感电流存在很大的谐波；当电感L取值比规定范围大时，实际电流不能快速跟踪给定电流；只有当电感L在规定范围内取值时，才能够实现快速跟踪给定电流和有效抑制谐波电流。

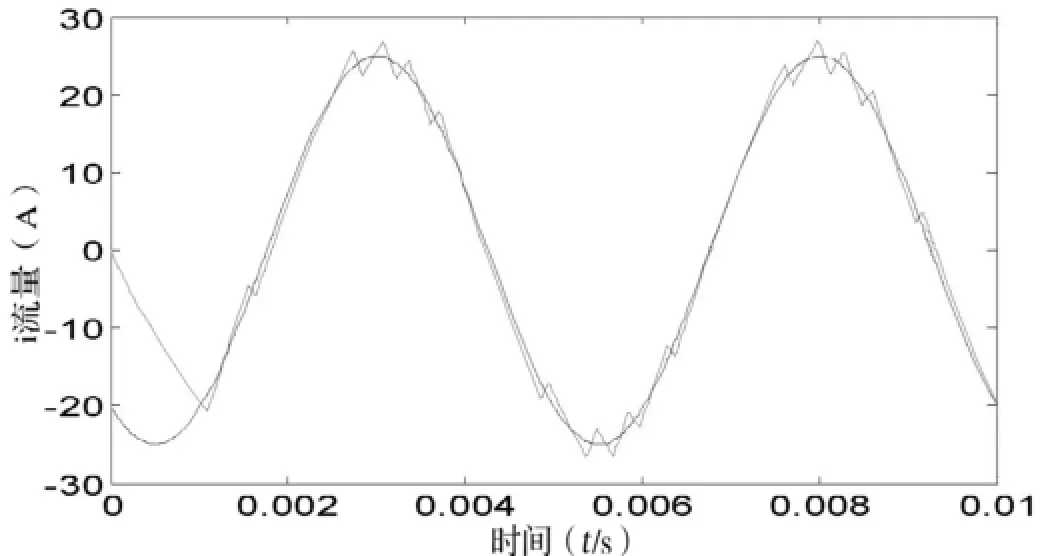
图9　电感L=15mH时的电流波形

4　结语

本文对单相交流电子负载的拓扑结构及滞环控制原理进行了简单的介绍，重点分析了交流侧电感参数的选取依据。通过建立数学模型，从快速跟踪给定电流、器件的开关频率限制和抑制谐波电流3方面综合分析，得出了电感参数的选取范围。最后通过进行仿真实验，证明了理论分析与实验结果的一致性，由此证明了本文所述方法的正确性与可行性。

［1］严雪飞，朱长青，赵月飞，等.交流电子负载中电感参数的选取［J］.电网与清洁能源，2014（6）：12-13.

［2］李春龙，沈颂华，卢家林，等.任意PF下单相PWM整流器电感参数的选择［J］.电力电子技术，2007（4）：64-65.

［3］张兴，张崇巍.PWM整流器及其控制［M］.北京：机械工业出版社，2012.

［4］潘诗锋.大功率交流电子负载的研究［D］.南京：东南大学，2005.

［5］黄海宏，王海欣，张毅，等.PWM整流电路的原理分析［J］.电气电子教学学报，2007（4）：28-30.

［6］齐焱.单相能馈式电力电子负载的研究［D］.哈尔滨：哈尔滨理工大学，2015.

［7］王雷.能量回馈型交流电子负载变换器研究［D］.南京：南京航空航天大学，2008.

［8］方露，党幼云，康鹏飞.交流电子负载电感参数设计［J］.西安工程大学学报，2015（4）：432-433.

Analysis of single phase AC electronic load inductance parameters

Jiang Xiuhao， Dang Youyun， Wang Xiangtao， Han Mingqi， Tu Zhan
（School of Electronics and Information， Xi’an Polytechnic University， Xi’an 710048， China）

The paper applies the single phase AC electronic load with current hysteresis control to the PWM rectifier circuit topology，but currently the selection of AC side inductance parameters is lack of theoretical basis. Firstly， it analyzes the fast tracking of a given current separately and gets the upper bound of the inductance parameter selection range. Secondly， the thesis compares witching frequency limitation with suppression of harmonic currents， obtains the lower limit of inductance parameter selection range， and eventually determines the selection range of the AC side inductance parameters. Finally， the feasibility of the inductance selection scheme is verified through the simulation experiments in Matlab/Simulink， which has a certain practicality.

PWM rectifier； electronic load； inductance parameter

江秀浩（1988— ），男，河南唐河，硕士；研究方向：电力电子与电力传动。