基于张量积Bézier曲面生成组合混沌系统的图像加密算法

张 永 红

(渭南师范学院 数理学院,陕西 渭南 714099)



【自然科学基础理论研究】

基于张量积Bézier曲面生成组合混沌系统的图像加密算法

张 永 红

(渭南师范学院 数理学院,陕西 渭南 714099)

给出了一种基于组合混沌系统的图像加密算法:首先,通过给定的密钥生成器,获得若干个混沌系统的初始值,利用所得初始值通过混沌系统生成若干个混沌矩阵；其次,利用张量积Bézier曲面的生成方法得到组合混沌矩阵,把所得的组合混沌矩阵和原始图像进行插值,得到插值图像；最后,把插值图像利用组合混沌序列进行置乱处理,从而得到最终的加密图像。数字实验表明,利用组合混沌系统进行加密具有较好的加密与恢复效果。

数字图像；混沌系统；插值；加密

0　引言

人们越来越关心日新月异的信息技术发展中的信息安全问题,如何能够保证信息量的完整性、可用性和保密性便成了信息安全技术中的一个最为基本的问题,在信息安全技术中一个最为必要的手段便是对信息的加密。

混沌现象是非线性动力学系统中的类随机过程的表现形式之一[1],目前广泛应用于信息安全中。利用混沌系统对信息进行加密主要是依赖该系统所生成的混沌序列的不可预测性[2-5]。文昌辞等[2,6]基于仿射变换和复合混沌系统提出了一种数字图像加密的新算法,该算法首先利用三维类仿射变换对数字图像进行初步加密,然后根据像素的坐标在置乱像素位置的同时对灰度值进行混合,最后按行交替进行非线性扩散和自适应替代,在替代过程中用图像信息扰动耦合的多个混沌系统从而进行自适应加密。郭银景等[3]基于三维Baker映射与复合混沌序列提出了一种数字图像加密算法,该算法分别选用了一维无限折叠映射和三维Baker映射对图像进行置乱,然后利用指数变换和一维Logistic映射对像素进行扩散处理。胡学刚等[4]结合一维与高维混沌系统的优点,基于一维Logistic系统和三维Lorenz系统提出了一种数字图像加密算法,该算法依据加密矩阵和数字图像自身特征,自适应地对每一个像素点选择不同的置乱和扩散变换等等。

现有的这些算法均是把不同的混沌系统混合起来应用于图像加密之中,这里基于张量积Bézier曲面生成思想,首先获得新的组合混沌系统,然后把该组合混沌系统应用于数字图像加密之中,从而给出了一种基于组合混沌系统的图像加密算法,该算法的思想是:首先,通过给定的密钥生成器,获得若干个混沌系统的初始值,利用所得初始值通过混沌系统生成若干个混沌矩阵；其次,利用张量积Bézier曲面的生成方法得到组合混沌矩阵,把所得的组合混沌矩阵和原始图像进行插值,得到插值图像；最后,把插值图像利用混沌序列进行置乱处理,从而得到最终的加密图像。

该算法的优点是首先生成了新的组合混沌系统,该系统的初始条件较多,从而在应用于图像加密时使得密钥空间大大增加,可以增大加密的安全性。数字实验表明,利用组合混沌系统进行加密具有较好的加密与恢复效果及良好的安全性与抗攻击性。

1　算法原理

1.1Logistic混沌系统

Logistic混沌系统[7]也被称为虫口模型,该混沌系统最早被用来描述和预测昆虫数目变化情况,由于其表述简洁、计算简单而被广泛应用。

Logistic混沌系统的迭代形式如式(1)所示:

xn+1=f(xn,μ)=μxn(1-xn)。

(1)

其中：初始值x0∈(0,1),当3.569 946 …≤μ≤4时,Logistic系统的输入和输出都分布在区间(0,1)上,并呈现混沌状态。图1给出了Logistic系统的分岔图。

图1　Logistic映射的分岔图

图2　组合混沌序列分布图

图3　组合混沌序列的初值敏感性

(2)

1.2张量积Bézier曲面

张量积Bézier曲面[8]定义为

(3)

张量积Bézier曲面改写成矩阵的形式为

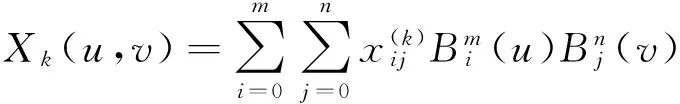
(4)

其中：参数u,v∈[0,1]。

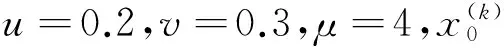
1.3加密与解密算法

Step1:输入大小为M×N的原始图像PI ,密钥序列K,μ,u,v,θ,λ,m,n;

通过线性变换

u=(1-θ)a+θb

(5)

Step3:将原图像矩阵PI和组合混沌矩阵ECM对应位置按照式(6)进行线性插值

MidPI=(1-λ)PI+λECM；

(6)

Step4:利用组合混沌序列对MidPI进行混沌置乱运算,从而得到加密图像EnI。

解密算法是加密算法的逆过程。

2　数值试验

为了验证所给算法的有效性,分别选取不同的原始图像进行试验,这里选取了Couple (64×64),Bridge(128×128),Camera(256×256),Lake(512×512),括号中的数字表示图像的大小。其中图4至图7中的(a)分别表示原始图像；图4至图7中的(b)分别表示加密图像,这里密钥选取:μ=4,u=0.2,v=0.3,K=qwertyuiopasdfgh,m=2,n=2,θ=0.1,λ=0.9;图4至图7中的(c)分别表示正确密钥的解密图像；图4至图7中的(d)分别表示错误密钥的解密图像,这里的密钥仅仅把K=qwertyuiopasdfgh改变为K=zwertyuiopasdfgh,其他密钥不改变。

从图4至图7中的(b)可以看出,该算法加密效果较好;从图4至图7中的(c)可以看出,该算法恢复效果较好；从图4至图7中的(d)可以看出,仅仅改变密钥序列K的一位(a改为z),原始图像便不能正确地恢复出来。从而可知,该算法具有较好的加密解密效果和较高的安全性。

图4　对Couple应用加密解密算法

图5　对Bridge应用加密解密算法

图6　对Camera应用加密解密算法

图7　对Lake应用加密解密算法

3　安全性分析

3.1密钥空间和初值敏感性分析

加密算法的安全性首先体现在其具有足够大的密钥空间[9],致使其能够更为有效地抵御暴力攻击。这里所谓的密钥空间是指所有应用于加密算法和解密算法的所有不同的密钥的总数[1]。该算法的密钥序列为K,μ,u,v,θ,λ,m,n。其中:K=K1K2…Kk,Ki(i=1,2,…,k)表示第i个位置字母或者数字的二进制表示; μ表示Logistic混沌系统的混沌参数; (m+1)× (n+1)表示需要的混沌序列的个数; u,v表示张量积曲面的参数; θ,λ表示线性插值所需参数。因此,密钥空间为2135(≈4.355 6×1040)。

图8　密钥敏感性分析

另一方面,密钥的敏感性也是一个理想的加密方案所必须的,即对密钥进行细微改变的时候,加密结果会完全改变[7]。图8针对Couple图像给出了密钥的敏感性分析,其中:图8(a)表示密钥正确时的解密图像,其密钥选取为:μ=4,u=0.2,v=0.3,m=2,n=2,θ=0.1,λ=0.9,K=qwertyuiopasdfgh；图8(b)(c)(d)分别表示密钥错误时的解密图像,这里仅仅改变密钥K中的某一位,分别选取K1=zwertyuiopasdfgh，K2=qxertyuiopasdfgh， K3=qwcrtyuiopasdfgh,其他密钥均不发生改变。从图8可以看出,当解密的密钥仅仅一位发生改变时,原始图像便不能被正确恢复出来,由此可知该算法具有较好的密钥敏感性,可以满足加密的安全性要求。

3.2直方图分析

直方图是用来表示数字图像变化情况的一种非常重要的工具。[10]利用直方图可以非常清楚地解析出图像的规则性,比较清晰直观地发现数字图像质量特性的分布状态,对于数字图像的分布状况可以做到一目了然,从而可以非常方便的判断出其总体质量的分布情况。

图9至图12分别给出了图像Couple、Bridge、Camera和Lake的加密实验的直方图，其中：图9至图12中的(a)表示原始图像的直方图；图9至图12中的(b)表示加密后图像的直方图,这里密钥选择：μ=4,u=0.2,v=0.3,m=2,n=2,θ=0.1,λ=0.9,K=qwertyuiopasdfgh；图9至图12中的(c)表示正确密钥解密图像的直方图；图9至图12中的(d)表示错误密钥解密图像的直方图,这里仅仅是把K=qwertyuiopasdfgh改变成为K1=zwertyuiopasdfgh,其他密钥不变。

图9　图像Couple的直方图

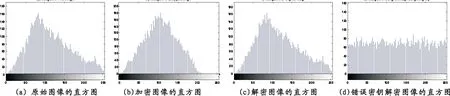
图10　图像Bridge的直方图

图11　图像Camera的直方图

图12　图像Lake的直方图

由图9至图12可以看出，原始图像与正确密钥的解密图像的直方图基本相像,加密图像和错误密钥解密图像的直方图与原始图像的直方图相差较大,由此可知该算法有效。

4　结语

本文提出了一种基于张量积Bézier曲面生成的组合混沌序列的方法,并将该组合混沌序列应用于数字图像加密中。首先利用特定的密钥序列生成若干个混沌初始值,进而利用张量积Bézier曲面生成了组合混沌序列,并把该混沌序列应用于数字图像加密之中。数字实验表明,利用组合混沌系统进行加密具有较好的加密与恢复效果和良好的安全性和抗攻击性。

[1] 廖晓峰,肖迪,陈勇,等.混沌密码学原理及其应用[M].北京:科学出版社，2009.

[2] 文昌辞,王沁,刘向宏，等.基于仿射和复合混沌的图像自适应加密算法[J].通信学报,2012,40(11):119-127.

[3] 郭银景,武光收,王萍，等.基于三维Baker映射与复合混沌序列的图像加密算法[J].山东科技大学学报,2008,27(6)：68-71.

[4] 胡学刚,王月.基于复合混沌系统的图像加密新算法[J].计算机应用，2010,30(5)：1209-1211.

[5] G.R.Chen,Y.B.Mao,C.K.Chui.A symmetric image encryption scheme based on 3D chaotic cat map[J].Chaos,Solitons and Fractals，2004,21：749-761.

[6] 文昌辞,王沁,刘向宏，等.基于仿射和复合混沌的图像加密新算法[J].计算机研究与发展,2013,50(2):319-324.

[7] 李彩虹,李贻斌,赵磊，等.一维Logistic映射混沌伪随机序列统计特性研究[J].计算机应用研究,2014,31(5)：1403-1406.

[8] Gerald Farin. Curves and Surfaces for Computer aided Geometric Design[M].Boston:Academic press,1984.231-251.

[9] 张永红.基于有理Bézier曲面生成组合混沌序列的图像加密算法[J].计算机科学,2015,42(4)：136-141.

[10] 张雪锋.混沌序列生成技术及其若干应用研究[D].西安:西安电子科技大学博士学位论文,2011.

【责任编辑牛怀岗】

An Algorithm of Image Encrypting Based on Multi-chaotic System Generated by Tensor Product Bézier Surfaces

ZHANG Yong-hong

(School of Mathematics and Physics,Weinan Normal University,Weinan 714099,China)

In this paper,an implementation of digital image encryption scheme based on the multi-chaotic system is proposed. The first,many initial conditions of Logistic chaotic system are generated by using the external secret key of 128-bit,and then many Logistic chaotic matrixes are generated; the second,the multi-chaotic matrix is generated based on tensor product Bézier surfaces; the third,the interpolation between plain-image and chaotic matrix is applied; finally,the chaotic address set is generated by using the multi-chaotic matrix,and then the permutation is given by using this chaotic address set. The algorithm has the advantage that both diffusion and scrambling are operated by using the multi-chaotic sequence. The results of several experimental,statistical analysis and key sensitivity tests show that the proposed image encryption scheme provides an efficient and secure way for real-time image encryption and transmission.

digital image; chaos map; interpolation; encryption

TP391.41

A

1009-5128(2016)12-0019-06

2016-03-14

陕西省教育厅科学研究项目：基于脊波和曲波的数字图像降噪技术研究(2013JK0569)；渭南师范学院特色学科建设项目：数学方法在秦东经济社会发展中的应用(14TSXK02)；渭南师范学院(省)扶持学科项目：基于小波的图像加密算法研究

张永红(1976—)，男,陕西合阳人,渭南师范学院数理学院副教授,理学硕士,主要从事计算机图形学及图像处理研究。