悬索桥施工误差对空缆线形的影响

曹　旭，陈香杰

(长安大学 公路学院，陕西 西安 710064)



悬索桥施工误差对空缆线形的影响

曹旭，陈香杰

(长安大学 公路学院，陕西 西安 710064)

悬索桥施工过程中，主缆空缆线形是非常关键的控制目标，其精确程度对成桥的质量具有决定性的影响，而主缆空缆线形受到很多因素的影响。以云南普立特大桥为依托工程，采用单因素分析法，用悬索桥主缆线形计算系统计算出所需数据以研究悬索桥施工误差对空缆线形的影响。以主缆空缆线形为控制目标，对悬索桥施工过程中各个参数的敏感性进行分析，结果表明：对空缆线形影响由大到小依次为：塔高、双塔纵偏、主缆弹性模量、主缆钢丝直径、钢箱梁重量、主缆钢丝容重。

悬索桥；参数误差；空缆线形

普立特大悬索桥位于云南省宣威市，跨越普立大沟深切峡谷，桥型为(166+628+166) m单跨钢箱梁悬索桥。全长1 040 m，桥面全宽28.5 m，桥面至沟谷底深达388 m，大桥位于云贵高原地区，自然环境复杂，施工过程中主缆线形影响因素较多。而悬索桥施工控制的首要任务是精确计算出空缆状态的线形，再以此为前提进行后续阶段的施工。文献[1]介绍了温度因素对悬索桥主缆线形的影响，并给出了相应温度下空缆线形的计算方法；文献[2]计算分析了主缆的弹性模量误差和截面积误差对施工线形的影响，并给出了很好的建议。本文在借鉴前人研究的基础上，从主缆、主塔、钢箱梁、索鞍方面，量化研究各个参数对主缆线形的影响，从而分析其敏感性。

1　参数误差及其影响分析

1.1主缆参数误差及影响分析

普立特大悬索桥主缆采用PPWS法。桥梁左右幅各有一根主缆，每根主缆由91根索股组成，单根索股由91根直径5.1 mm的镀锌高强钢丝组成。在横桥向，两根主缆中心距离为26 m，钢丝标准抗拉强度为1 670 MPa，索股两端采用热铸锚头。架设过程中索股为正六边形，入索鞍部分索股变成了正四边形，其他部分形状不变。

在影响主缆空缆线形的因素中，除了主缆弹性模量和钢丝容重等因素外，主要因素还有钢丝直径，在钢丝直径有误差时，将会影响单股的截面积，从而影响单缆的横截面积。主缆在制作时，弹性模量范围为(2.0±0.1)×105MPa,误差范围为(-0.1×105～0.1×105) MPa。钢丝直径范围为(5.10±0.06) mm，误差范围为(-0.06～0.06) mm。

1.1.1主缆弹性模量对空缆线形的影响

从参数误差分析可知主缆弹性模量在制造时的误差范围为(±0.1)×105MPa，在施工中主缆弹性模量取值为1.98×105MPa。为了更加精确清晰的分析参数的影响规律，分别取主缆弹性模量为1.88×105、1.90×105、1.92×105、1.94×105、1.96×105、1.98×105、2.00×105、2.02×105、2.04×105、2.06×105、2.08×105MPa进行模型计算，计算主缆空缆线形。由于悬索桥主缆是柔性体系，主缆空缆各点坐标，是由悬链线公式唯一确定的。所以在分析主缆空缆线形时，仅分析主缆两个边跨和主跨的跨中标高即可以确定整个主缆的空缆线形。

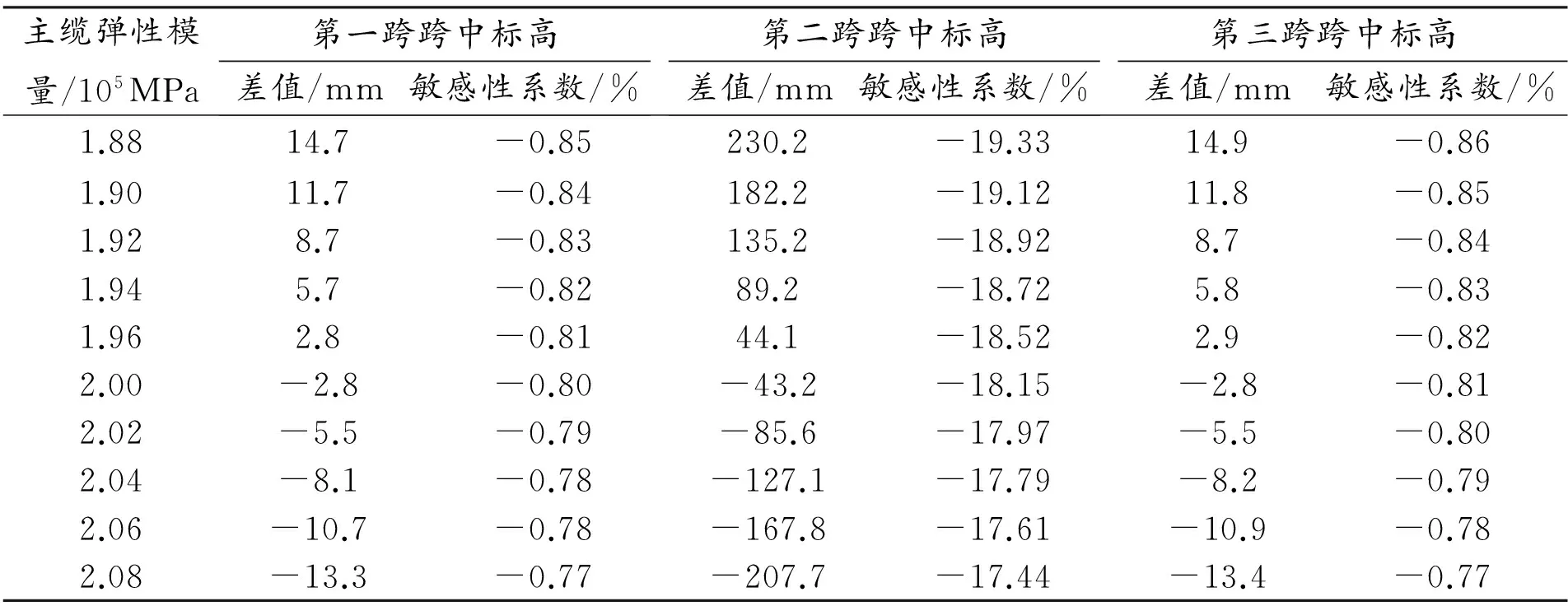
表1　主缆空缆线形敏感性分析表

主缆跨度为(166+628+166) m，分析表1可得，主缆取不同的弹性模量时，两个边跨的误差值基本上是一致，所以图1中，第一、第三边跨的分析线基本上是重合的。随着主缆弹性模量的增大，悬索桥三跨跨中标高均是逐渐减小的，成反相关的关系，且基本上是线性变化。主缆弹性模量取1.88×105MPa时，两个边跨的跨中标高分别增加了14.7 mm和14.9 mm，但是跨中标高增大230.2mm，反之取2.08×105MPa时，两个边跨跨中标高分别降低了13.3 mm和13.4 mm，跨中标高降低了207.7 mm。分析可得，主缆弹性模量是影响主缆空缆线形的重要因素之一。

1.1.2主缆钢丝直径对空缆线形的影响

从上面参数分析可知，主缆钢丝束在制造时的误差范围为±0.06mm，为了更加精确清晰的分析参数的影响规律，取主缆钢丝直径分别为5.04 mm、5.06 mm、5.08 mm、5.10 mm、5.12 mm、5.14 mm、5.16 mm，进行模型计算。分析主缆空缆线形时，仅分析悬索桥各跨跨中标高的变化量，坐标(0,0)点取在普立岸散索鞍的IP点处。

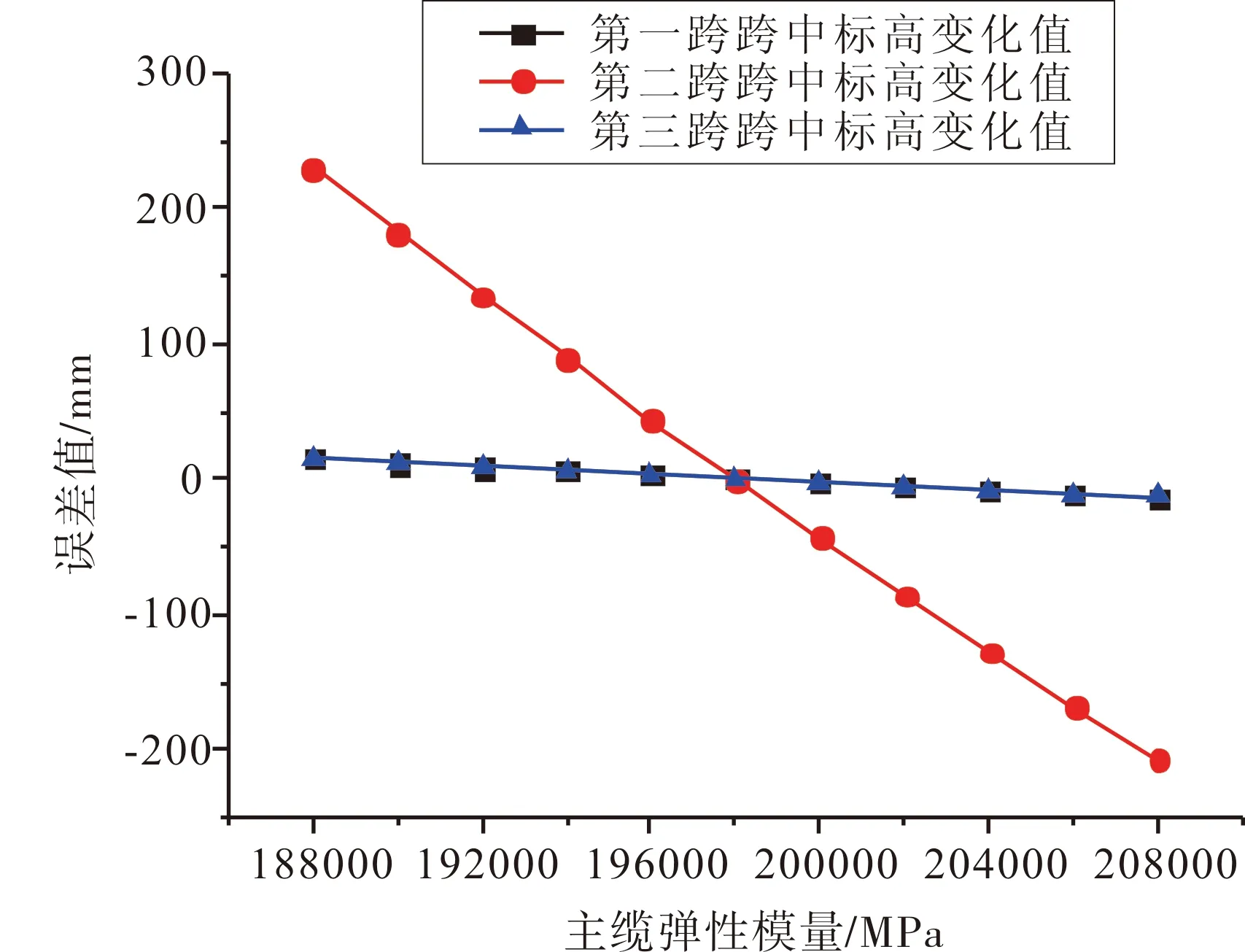
图1　主缆空缆线形敏感性分析图

图2　主缆空缆线形敏感性分析图

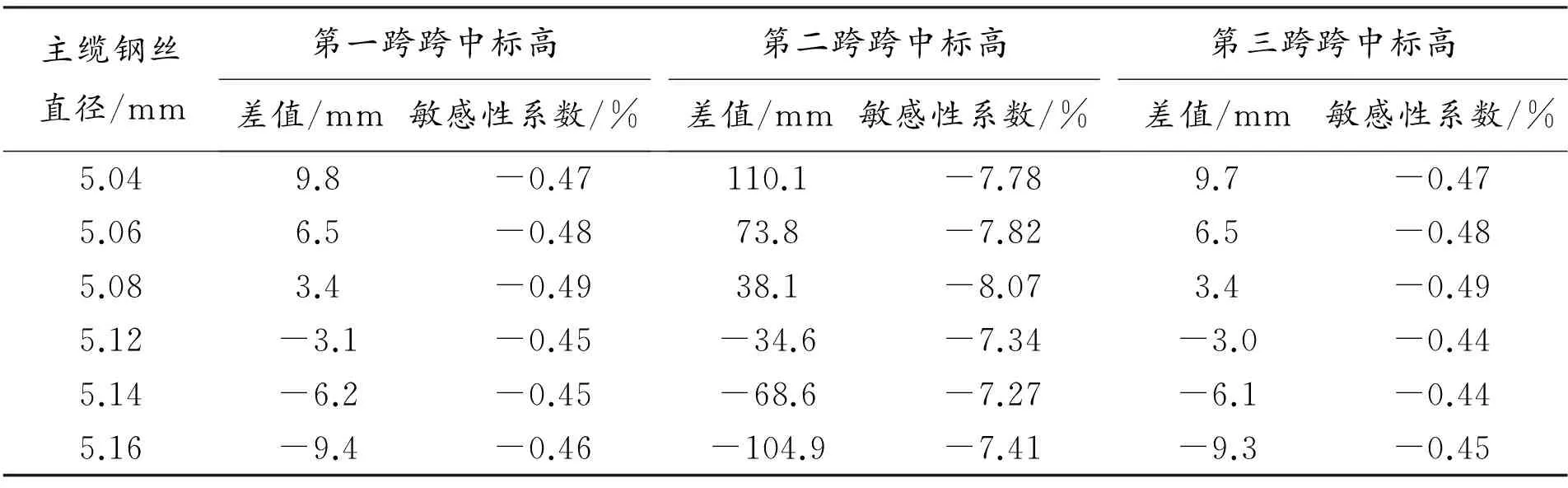
主缆钢丝直径/mm第一跨跨中标高差值/mm敏感性系数/%第二跨跨中标高差值/mm敏感性系数/%第三跨跨中标高差值/mm敏感性系数/%5.049.8-0.47110.1-7.789.7-0.475.066.5-0.4873.8-7.826.5-0.485.083.4-0.4938.1-8.073.4-0.495.12-3.1-0.45-34.6-7.34-3.0-0.445.14-6.2-0.45-68.6-7.27-6.1-0.445.16-9.4-0.46-104.9-7.41-9.3-0.45

从表2和图2分析可得，当主缆钢丝直径取值5.12 mm时，跨中空缆的标高已经减少了34.6 mm，当取值5.04 mm时，跨中空缆标高增高了110.1 mm，主跨为628 m，这个影响相当明显。边跨的影响并不很明显，当主缆钢丝直径分别取最小值和最大值时，标高值分别增加了9.8 mm，减少了9.4 mm。从图2可以看出：随着主缆钢丝直径的增大，主缆空缆线形是逐渐降低的，即成反相关的关系，并且基本上成线性的关系在变化；第一、第三跨的分析影响线基本上是重合的，所以两边跨的变化基本上是一致的；主缆钢丝直径对主缆空缆线形的影响是较明显的。

1.1.3主缆钢丝容重对空缆线形的影响

在分析悬索桥主缆状态时，主缆容重不同时，主缆的自重荷载会不同，将会影响悬索桥的成桥状态，为了使悬索桥的成桥状态达到设计的基准状态，所以在施工过程中，主缆空缆线形可能会与设计的空缆线形有一定的偏差，施工中取其容重为78.5 kN/m3，主缆容重取不同值时，主缆空缆线形的变化规律如表3和图3所示。

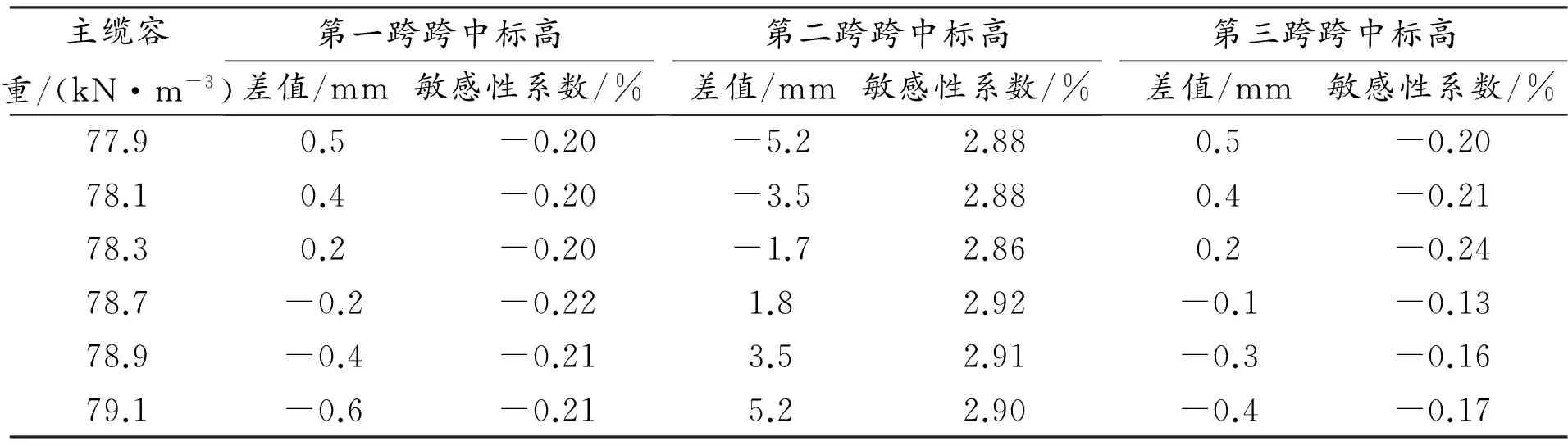
表3　主缆空缆线形敏感性分析表

分析图3和表3可得，主缆容重在77.9 kN/m3～79.1 kN/m3之间变化时，主缆的空缆线形变化也是十分微小的。当主缆容重取77.9 kN/m3，第二跨跨中的空缆线形比设计基准值仅低了5.2 mm。两边跨的分析影响线基本上是重合的，说明两边跨的空缆标高变化随着主缆容重的变化基本上是一致的。主跨空缆线形与主缆容重是正相关的关系，两边跨空缆线形与主缆容重是反相关的关系。总之，主缆容重对主缆空缆线形的影响不明显，当主缆容重在误差允许范围内时，可以不予考虑此误差对空缆线形的影响。

图3　主缆空缆线形敏感性分析图

1.2主塔参数误差及影响分析

在考虑主塔对悬索桥主缆空缆线形的影响时，主要考虑主塔的两个参数，一是主塔的塔顶标高变化，二是塔顶的纵向偏位。

普立特大桥跨过普立大沟，受自然因素的影响很大，最高的塔高达到153.5 m，考虑到主塔混凝土的收缩徐变和主塔的基础沉降，将会使塔顶标高有一定的变化，从而影响主缆状态参数。悬索桥在架设主缆的过程中，主塔在猫道和已经架设的索股等的作用下，在桥梁的纵桥方向将会受到不平衡力的作用，所以在纵桥方向上将会有一定的塔偏，也会影响主缆空缆线形。

1.2.1塔高变化对空缆线形的影响

在分析塔高变化对主缆状态的影响时，从三个方面进行考虑：(1) 4号塔高的变化(普立岸主塔)；(2) 5号塔高的变化(宣威岸主塔)；(3) 4和5号主塔塔顶标高同时比设计基准值增大或者减小。

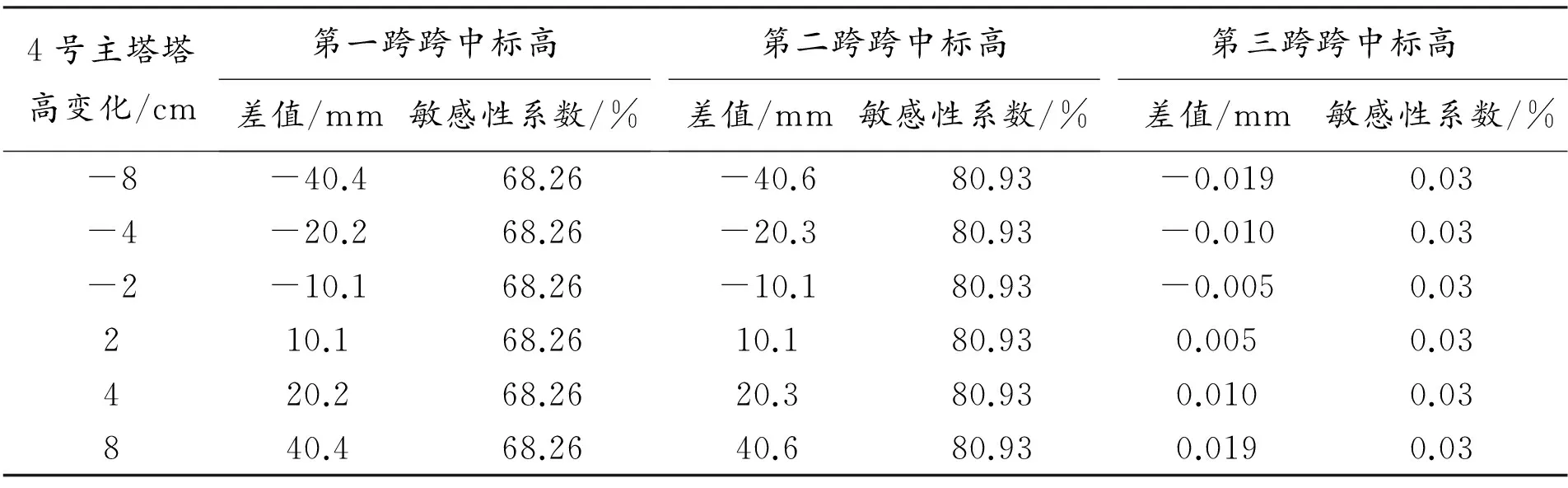
表4　4号主塔塔高变化时主缆空缆线形的敏感性分析表

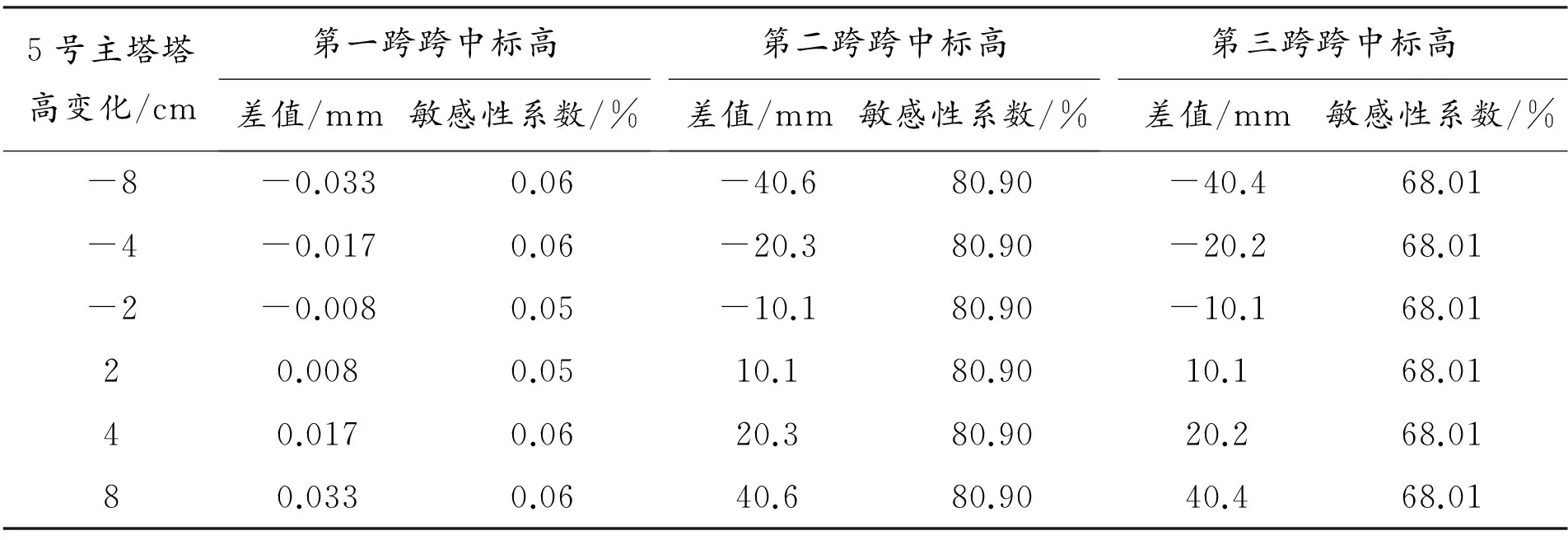
表5　5号主塔塔高变化时主缆空缆线形的敏感性分析表

表6　双塔塔高同时变化时主缆空缆线形的敏感性分析表

由表4可知，在4号主塔塔高单独变化时，受影响最大的主要是第一跨和第二跨的主缆线形，对第三跨的主缆线形基本上没有影响。对第一跨和第二跨的影响误差值基本上是相等，但是，由于跨度的不同敏感性还是有区别的。塔高与主缆线形是正相关的关系且基本上呈线性变化。

由表5可知，5号主塔塔高单独变化时，结果刚好与4号主塔单独变化时的结果相反，对第二跨和第三跨的主缆线形影响是很大的，最大的已经达到4 cm，且其影响基本上是一致的影响程度，对第一跨的主缆线形基本上没有影响。从分析中可以看出，主塔高度变化与主缆线形的变化是正相关的关系且基本上是呈线性变化的关系。

由表6可知，主跨的跨中标高变化基本上是两个边跨的两倍，两边跨的变化在误差值上基本上是相同的，主跨主缆最大变化值已经达到了8 cm，这种影响是不容忽视的。主塔塔高变化与主缆线形的变化是正相关的关系，且在一定范围内呈现出线形变化的关系。

从上面分析主塔塔高变化对主缆线形的影响可以总结出，当单主塔塔高单独变化时，基本上仅影响变化塔高两侧主缆的线形，且主缆跨中的标高变化值基本上是一致的。当两塔高同时变化时，三跨的主缆线形均会变化，且主跨的跨中标高值基本上是两边跨跨中标高变化值的两倍。主塔塔高变化与主缆线形变化基本上均是正相关的关系，且呈现线性变化的关系。

1.2.2塔纵偏对空缆线形的影响

分析主塔纵偏对主缆状态的影响，在保证普立特大桥三跨全长960 m不变的前提下，同理从三个角度考虑:(1) 4号主塔单独纵向偏位；(2) 5号主塔单独纵向偏位；(3) 4和5号主塔同时纵向偏位，指两主塔纵偏的方向相反，同时使主跨增大或者同时使主跨减小。

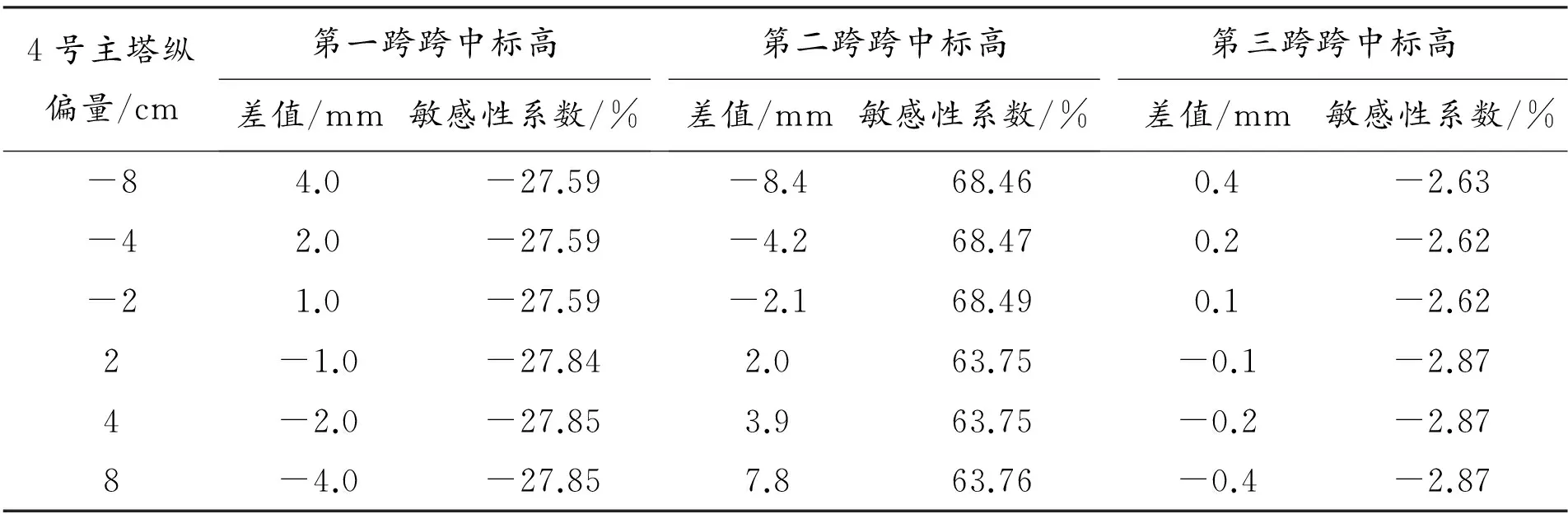
表7　4号主塔单独纵偏时主缆空缆线形的敏感性分析表

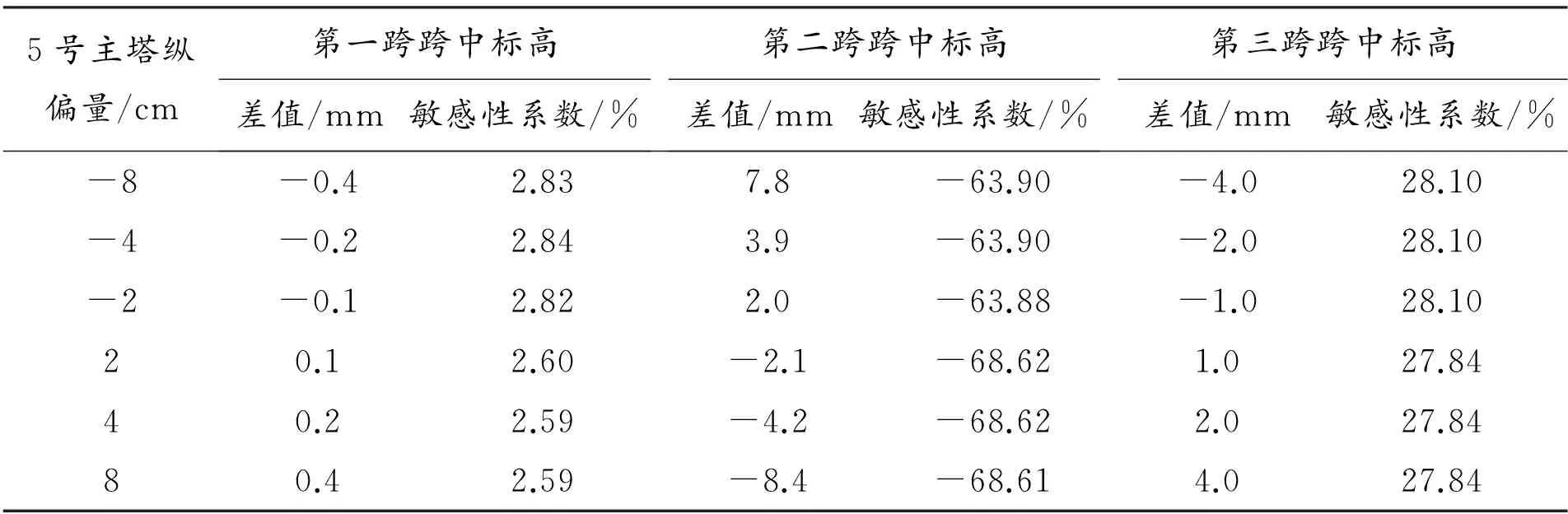
表8　5号主塔单独纵偏时主缆空缆线形的敏感性分析表

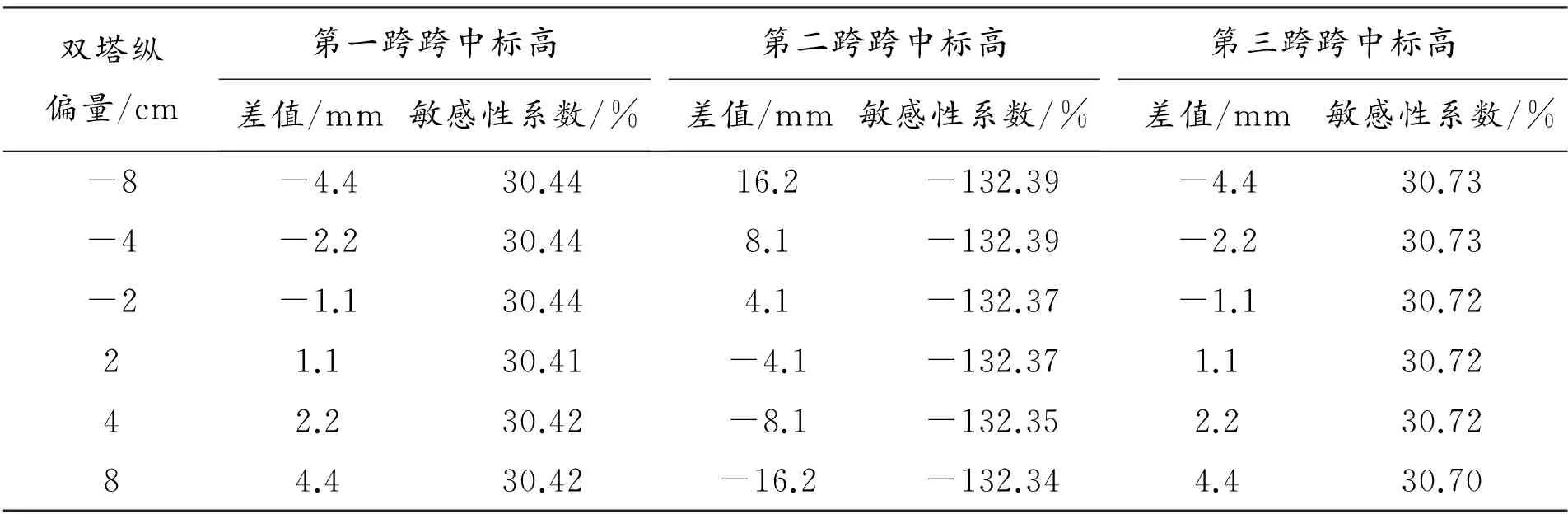
表9　双塔同时纵偏时主缆空缆线形的敏感性分析表

从表7可得，4号主塔纵偏对主跨跨中标高的影响最明显，第一跨次之，第三跨的影响最小。虽然最大的影响值仅有8.4 mm，但是敏感性系数则达到了68.4%，主塔纵偏量与主缆空缆线形标高变化量基本呈线性变化。

从表8可得，5号主塔纵偏的分析同4号主塔纵偏相同，主塔纵偏使得主跨跨度由小到大的变化过程中，均是主跨空缆线形标高逐渐减小，边跨主缆空缆线形标高逐渐增大。5号主塔纵偏与主缆空缆线形成线性变化的关系。

从表9可得，双塔纵偏量值是指两主塔各自的偏量，在主跨跨度由小变大的过程中，主跨空缆线形标高是逐渐减小，两边跨的空缆线形标高逐渐增大，且两边跨的变化过程基本相同。两主塔在相反方向各偏8 cm时，主跨标高变化最大为1.62 cm，敏感性系数也是相当大。双塔纵偏量与主缆空缆线形标高变化量呈线性变化的关系。

在普立特大桥全桥960 m一定的前提下，主塔纵偏使得主跨跨度从减小到增大的过程中，主跨空缆线形标高是由增大逐渐减小的，两边跨的主缆空缆线形由减小逐渐增大。预偏量与主缆空缆线形标高变化量基本上均是呈线性变化的关系。

1.3钢箱梁重量误差及影响分析

在计算悬索桥主缆空缆线形时，需要精确的确定钢箱梁的重量，因为钢箱梁的重量和其上面的二期恒载是通过吊杆传递给主缆。通过称重得出钢箱梁重量误差范围在±2 t内。

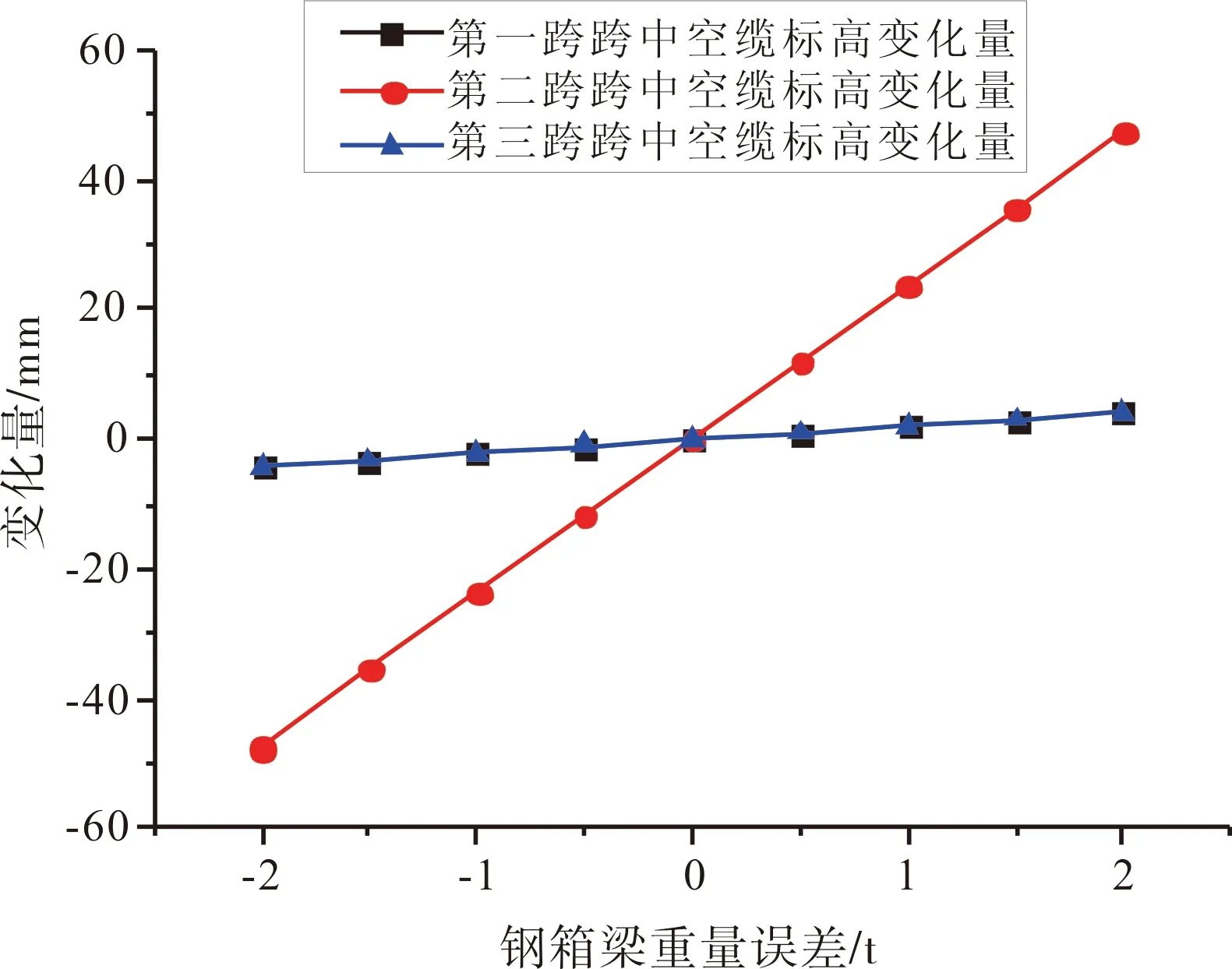
图4　主缆空缆线形敏感性分析图

由图4可知，随着钢箱梁重量的增加，主缆空缆线形比设计基准线形提高了，为了达到设计成桥基准线形，只有空缆线形提高的情况下，钢箱梁重量增加后，才能达到设计成桥线形。钢箱梁重量变化2 t时，主跨空缆线形变化4.7 cm，这个数值是不容忽视的。两边跨的分析影响线基本重合，说明两边跨的空缆线形变化基本一致。钢箱梁重量变化对主跨的空缆线形标高影响比较大，与三跨的空缆线形变化基本上均是成线性变化的关系。

2　主缆空缆线形影响因素主次分析

根据以上分析，现取所有参数的敏感性系数均值进行对比分析，得出其对空缆主缆线形影响的大小情况，见表10。

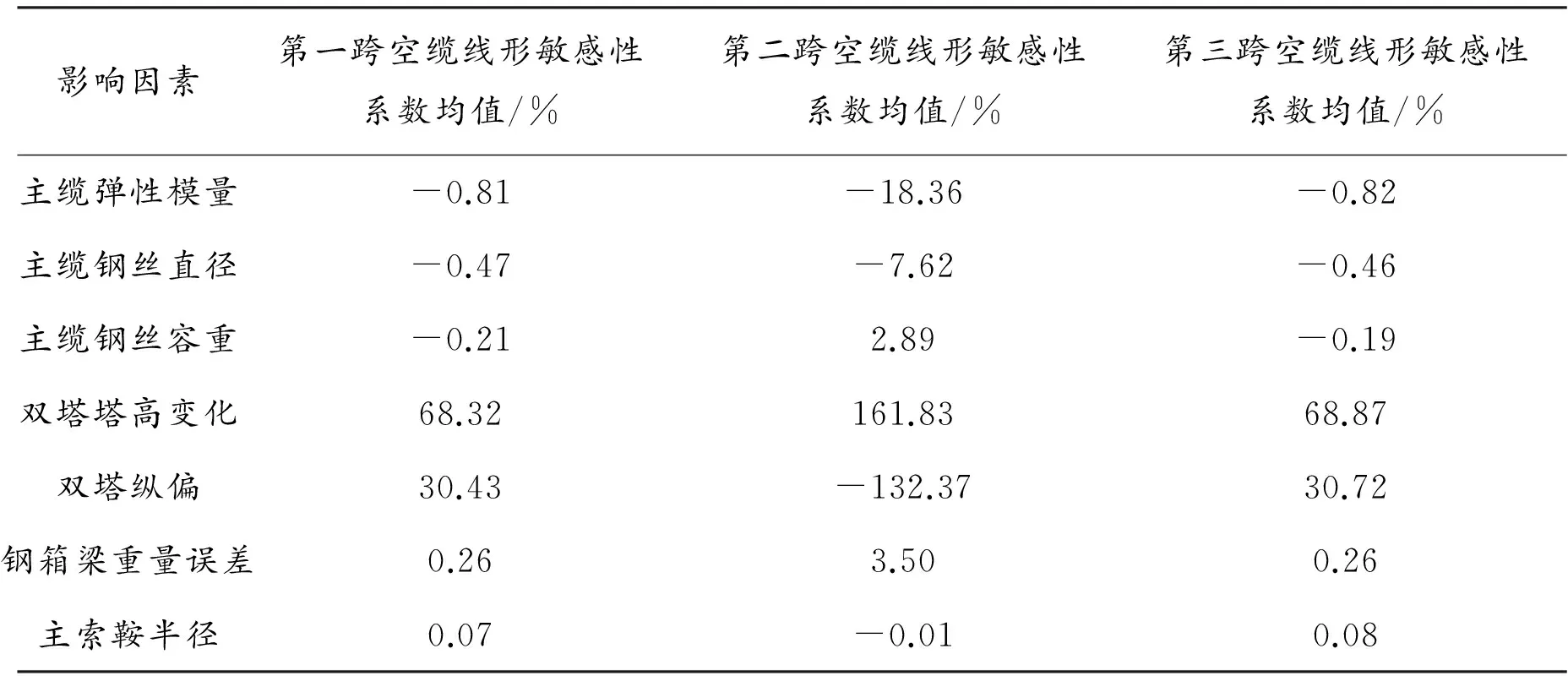
表10　主缆空缆线形影响因素主次分析表

由表11可知，对于第一、第二、第三跨，各个参数的影响敏感性系数均值大小虽不同，但其影响规律变化是一致的。对主梁空缆线形的影响由大到小依次为：双塔纵偏、塔高变化、主缆弹模、主缆钢丝直径、钢箱梁重量、主缆钢丝容重、主索鞍半径。

3　结语

(1)悬索桥主缆在生产过程中具有一定的生产误差，从而对空缆线形有一定影响。在主缆参数误差中对空缆线形影响最大的为主缆弹性模量，对于中跨敏感性系数为18.36%，是比较大的影响因素之一。因此主缆在制造过程中应该尽量减小误差，符合制造要求，以使空缆达到预期线形目标。

(2)主塔施工误差因素主要由施工引起，在施工中主塔与温度和混凝土自身收缩徐变有很大关系，因此塔高、塔偏相对难以控制。但从敏感性系数来看，塔高塔偏误差对空缆线形影响都是很大的，分别为161.83%和132.38%。因此，主塔在施工过程中要严格按照施工图纸施工，同时要考虑温度和混凝土等外界因素的影响，以使主塔施工趋近理论值，减小对主缆空缆线形的影响。

(3)钢箱梁重量对空缆线形影响相对较小，钢箱梁在预制时尽量减小制造误差，施工时确保钢箱梁的焊缝密实度以减小对空缆线形的影响。

[1]孙永明,张连振,李忠龙.自锚式悬索桥吊索目标索力影响参数分析[J].桥梁建设,2015(4):69-74.

[2]杜善明.大跨度悬索桥主缆线形影响参数分析研究[D].西安:长安大学,2014.

[3]向中富.桥梁工程控制[M].北京:人民交通出版社,2011.

[4]罗喜恒.悬索桥基准索股的空缆状态[J].结构工程师,2004(3)：21-26.

[5]于琦.悬索桥主缆施工参数及温度校准研究[D].西安:长安大学,2014.

[6]田芳.大跨度悬索桥的参数研究与静动力分析[D].北京:北京交通大学,2011.

[7]齐东春，沈锐利.悬索桥空间缆索主缆线形的计算方法[J].铁道建筑,2013(4):13-16.

[8]许腾.悬索桥施工误差对吊索长度的影响[J].重庆交通大学学报(自然科学版),2013，32(5):915-917.

[9]叶志龙.悬索桥主缆架设误差影响分析及参数控制[D].成都:西南交通大学，2008.

Influence of construction error on free cable shape of suspension bridges

CAO Xu，CHEN Xiang-jie

(School of Highway,Chang’an University,Xi’an 710064,China)

Free cable shape is the critical control target in suspension bridge construction process and its accuracy has a decisive effect to the quality of the bridge though it is affected by many factors.Based on Yunnan Puli super bridge engineering,using the single factor analysis method,with the main cable shape of suspension system to calculate the required data to study the influence of construction error on empty cable shape of suspension bridges.For goal of controlling the shape of free cable,the sensitivity of each parameter in the process of suspension bridges construction is analyzed.The result showed that the effect sequences of factors for free cable shape are as follows:temperature,tower height,tower deviation,elastic modulus of main cable,diameter of main cable wire,steel box girder weight,main cable wire density.

suspension bridge;parameter errors;free cable shape

2016-03-15

云南省交通运输厅科技计划项目(云交科2013(A)02)

曹旭(1991—)，男，河南民权人，硕士研究生。

1674-7046(2016)04-0053-07

10.14140/j.cnki.hncjxb.2016.04.011

U445

A