山地典型地形下的2 MW风力机仿真研究

■ 庞博邓胜祥（1.中南大学能源科学与工程学院；2.长沙理工大学可再生能源电力技术湖南省重点实验室）

山地典型地形下的2 MW风力机仿真研究

■ 庞博1*邓胜祥1，2
（1.中南大学能源科学与工程学院；2.长沙理工大学可再生能源电力技术湖南省重点实验室）

根据我国中部某实测地的山地狭管及风速数据，使用Solidworks建立2 MW风力机模型，并分别建立了风力机在平地与狭管中的计算域模型，然后通过ICEM划分网格，用Fluent软件对模型进行仿真。仿真结果表明，额定风速下，平地风力机输出功率比理论值低，与平地相比，狭管对流体有明显的加速作用，可使狭管风力机比同入流风速下的平地风力机功率高约5.0％ ～43.5％。研究结果为在山地狭管中布置风力机提供了参考。

复杂山地；CFD仿真；输出功率；狭管效应；水平轴风力机；流场分布；Wilson理论

0　引言

随着我国风电产业的高速发展，风电场的选址地点逐渐从沿海与西部地区向内陆发展，地形逐渐从平地向山地、丘陵等复杂地形转变，而提高风电场发电效率的关键是在电场宏观选址区域进行科学的微观选址。山地狭管是山地与丘陵地带常见的一种地形，当气流流经山地狭管时，由于空气质量不能大量堆积，其将加速流过狭管，可以显著提高此段风力机的输出功率[1,2]。

目前国内外关于地形对风力机运行过程的研究主要集中在数值仿真与实验模拟两方面。1)实验方面：通常集中在单一风力机或纯地形研究领域，鲜见有人将这两方面结合研究。哈尔滨工业大学的郭文星[3]对二维山坡、二维山脊、三维轴对称山丘的典型模型风电场进行了实验研究，并与CFD仿真结果进行了对比，肯定了数值模拟的准确性。2)数值模拟方面：荷兰海事研究所的Michel Make等[4]应用试验结合数值模拟，对比研究了两种型号风力机表面的扰流情况，结果表明数值模拟能准确计算出风力机运行的情况。

现今，国内研究者主要使用两类国外商业软件进行山地风力机研究与选址，一类以丹麦KAMMWAsP、美国Meso Map、加拿大WEST为代表，采用中尺度气象模式与小尺度模式结合分析，不适合分析局部细微流场；另一类以丹麦WAsP、英国Windfarm和法国Meteodyn WT为代表，采用标准线性流动模型，但在陡峭地形往往会过高估计此地形的风速[5]。

本文利用Wilson理论建立了山地风力机模型，并利用CFD 方法对平地风力机与狭管风力机进行数值仿真，研究了两种地形下风力机在多风速下的功率-速度曲线、额定输出功率条件下的流场分布情况。结果表明，CFD模拟出的风轮转矩值与风力机尾流发展结果，考虑了山体对风力机的影响、压力与湍耗散的存在，比理论计算更精确地展示风力机运行的真实情况，而合理的功率损失也验证了数值计算的正确性。

1　建立数学模型

1.1数学模型

仿真基于稳态不可压缩三维定常雷诺时均N-S方程(RANS)进行数值模拟，采用剪切压力输运SST k-ω湍流模型使方程组封闭；求解器采用Segregated隐式三维稳态算法、 SIMPLE压力-速度耦合算法；通用控制方程的离散采用有限容积法；对流项差分采用二阶迎风格式[6-8]。过程如下：

不可压缩流体连续性方程：

雷诺时均N-S方程(RANS)：

比耗散率ω方程：

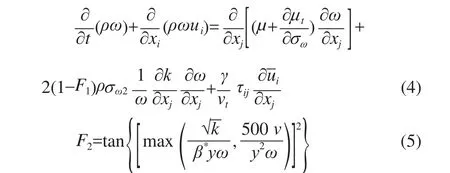
湍动能k方程：

式中，ui为速度；τij为粘性切应力；F1、F2为混合函数，F2用来修正F1在自由剪切流中的误差；y 为网格点到最近壁面的距离；v为分子运动粘度；uj为速度分量；t为时间；P为压力；σω、 σω2、β*为3个封闭常数；为分子动力粘度；为湍流动力粘度；Fi为质量力；上标“ ′ ”为脉动值。

1.2Wilson叶片建模理论

Wilson理论较于Schnlitz理论，考虑了涡流损失因素；相对于Glauert理论，考虑了叶尖损失与升阻比对气动性能的影响；且理论本身考虑了轴向与周向诱导因子，是当前最合理的叶片设计理论。其核心思想就是要使各叶素的风能利用系数Cpr达到最大[5,9]，如下：

半径r处风能利用系数：

半径r处尖速比：

式中，ar为半径r处轴向诱导因子，0＆lt;ar＆lt;1；br为半径r处周向诱导因子，0＆lt;br＆lt;1；Ftr为半径r处叶尖损失系数，0＆lt;Ftr＆lt;1； λr为半径r处的尖速比；Cpr为半径r处风能利用系数；βr为半径r处入流角；ω为叶轮转速；B为叶片数；R为叶轮半径；Vc为来流风速。

2　建模与网格划分

2.1风力机与狭管建模

本文根据湖南某地一年风塔实测风资源数据确定风力机参数，设计风速11.5 m/s，风轮额定转速17 r/min，风力机机电效率81％，风能利用系数Cp=0.4，尖速比为7，轮毂半径1.5 m。使用Wilson法，通过 Matlab计算出如图1所示的2 MW风力机沿叶片展向各叶素的原始安装角与弦长；然后采用6阶拟合，得到图2所示的安装角与弦长拟合曲线，拟合曲线相关系数的平方(R2)分别为0.9988与0.9971。Solidworks风力机叶片建模结果如图3所示。

图1　沿叶片各叶素的原始弦长与安装角

本文使用Global Mapper提取已公开的测风塔实测地STRM高程数据，并划分实测地狭管区域的等高线，将其导入Solidworks中，适当优化后建立狭管模型。选取狭管渐缩段之后布置风力机，狭管与风力机模型如图4所示，主要尺寸为入口谷宽408.9 m、谷底宽118.1 m、风力机距入口159.8 m。

图2　沿叶片各叶素的拟合弦长与安装角

图3　叶片模型

图4　狭管、风力机模型及尺寸

2.2计算域建模与网格划分

本文分别布置了平地风力机与狭管风力机地形，并根据最小经验尺寸进行计算域划分，仿真后确定没有边界对模型仿真造成影响[10]。其中，平地计算域如图4所示，长28D、宽8D、总高5.35D、风力机距计算域前端3D。由于狭管地形尺寸较平地大，为了准确模拟此地形下游远场尾流的发展情况，计算域扩大为长60D、宽26.08D、高10D、风力机距计算域前端9D，如图5所示。

图4　平地计算域模型及尺寸

图5　狭管计算域模型及尺寸

为提高计算的准确性与效率，全部模型均采用ICEM划分网格，综合考虑分块合理性与计算效率，除如图6a中叶轮较小的“Y”型域采用非结构网格，其他计算域均采用结构网格划分；为提高狭管地形仿真的可靠性，在如图6b所示的山体间区域专门划分了一个域提高网格的密度和质量；两个计算域均采取了合理的渐变网格策略以提高计算的效率[11,12]。

图6　叶轮与狭管区域网格划分

对于平地风力机计算域，本文从约120万网格开始，对压力梯度较大部分每次增加10万～15万网格，并进行额定风速11.50 m/s的计算，直至最终风轮转矩值无明显变化，最终选择1726452个网格的方案。对于类似狭管风力机计算域的，从约200万网格开始计算比较，风速设定为11.50 m/s，最终选择2916723个网格的方案[13]。

3　结果与讨论

3.1速度分析

本文所有云图均以叶轮轮毂中心为(0,0,0)原点。由于来流风速的扰流、叶轮圆周运动、塔架的干扰等因素，空气在流经风力机时将产生较强的湍流，进而会在尾流中产生扰动，增大这些地方的速度梯度[14]。

图7从原点后30～2230 m，每隔440 m做一个切片，共6个。切片1可发现由于塔架的存在，叶轮下部有一块速度渐变的方形区域；因为风驱动风轮转动产生力矩，而桨叶对气流产生反转矩作用，两叶片间的扇形区域速度从前叶片至后叶片逐渐增大，符合风力机旋转尾迹理论；受叶片阻挡的影响，叶片后部的半径略大于叶轮的“Y型”区域内速度梯度变化较大，区域直径约为1.5D～2D；从切片2～6可发现，随着距离的增加，低速尾流区域发展成了端部为圆的“Y型区域”，影响范围扩张速度适中，至风力机下游2230 m的切面6处，速度变化微小且均恢复到10.75 m/s以上，气流已趋于稳定。

图8为平地计算域风速-Y轴曲线，Y轴穿过轮毂与机舱的中轴线，可看出受风轮影响，风速在风轮前端快速下降，至轮毂表面处降至0 m/s，而在机舱后部风速迅速升至约9 m/s，接着平稳上升，至风力机后方1700 m处已恢复至10.50 m/s。

图8 平地风力机风速-Y轴曲线

图9为原点上方30 m处Y切面风速云图。可看出，受风力机与山体间的扰流影响，分布明显比平地时复杂得多，两座山体外侧形成了高速尾流带，两座山体与风力机后部明显出现了3条低速尾流带，同时风力机与两侧山体间则形成了2条高速尾流带，类似于射流卷吸效应，使风力机后的低速尾流带在约-220 m处迅速分叉，于约-1000 m处消失。而两座山体由于外形差异导致尾流差别很大，左侧山体内部向狭管凸出、外部有一断崖，使得流体较难绕到山体后侧，增强了其低速尾流带，可影响到-800 m后；右侧山体内部凹陷、整体呈圆锥台状，流体容易绕流，使其低速尾流带较弱，于约-400 m处消失，但中低速区域都可影响到-4500 m处。

图9 狭管计算域Y=30 m切面风速

图10为狭管计算域风速-Y轴曲线，Y轴穿过轮毂与机舱的中轴线。可看出，风速受狭管影响加速，至风力机前方达到11.80 m/s；接着在风轮前端快速下降；受狭管内高风速的影响，在机舱后部风速迅速升至约11.65 m/s；至狭管尾部渐扩段且受尾流影响，风速降至约6.5 m/s；接着由于受两边高速尾流带影响，尾流分叉，风速快速升到约10 m/s直至末端。

图10　沿Y轴狭管风力机风速

3.2全风速段功率分析

本文对平地风力机与狭管风力机从风力机切入速度3.00 m/s至额定功率速度11.50 m/s分别做了仿真，并与各风速的理论输出功率值进行了对比，如图11所示。由于考虑到实际情况并未将叶片设成光滑表面，且Wilson方法未考虑轮毂损失、尾流损失因子、叶轮受塔架回流等因素的影响，因此平地风力机输出功率较理论值有一定减小，但变化幅度并不大。而因为狭管对来流明显的加速能力，使狭管风力机在各个风速条件下的输出功率都明显高过平地与理论风力机的功率值，且狭管风力机可在风速较低时就达到风力机额定输出功率2 MW，从而使风力机在更广阔的风速段获得额定发电功率。

图11 全风速段3种风力机输出功率

图12展示的是理论、狭管及平地风力机三者间的差值。可从此图直观看出3条差值曲线的斜率呈不同程度的增大，且有关狭管风力机的2条曲线的斜率明显更大。平地-理论差值升高较慢，最大值位于11.60 m/s附近，在140 kW以下。而有关狭管风力机的2条差值曲线均在9.60 m/ s附近达到最大值，此处平地-理论差值约为80 kW，而狭管-理论差值＆gt;750 kW，占2 MW理论功率的37.5％，是同风速下平地-理论差值的9.38倍，是平地-理论最大值的5.36倍；另外，此风速狭管-平地差值约为870 kW，为2 MW理论功率的43.5％，是同风速下平地-理论差值的10.88倍，是平地-理论最大值的6.21倍。

图12　各风速下3种风力机功率差

4　结论

1)狭管区域对流经其内的流体有明显的加速效果，从而可明显提高风力机的输出功率。对于本文建立的2 MW风力机，在入口风速约9.6 m/s时，狭管对风力机功率的提升达到最大，比同风速条件下的平地风力机高870 kW，占2 MW理论功率的43.5％，是同风速下平地-理论功率差值的10.88倍，功率提升效果十分明显。

2)从切入风速3 m/s至额定风速11.5 m/s，狭管对功率提升的效果逐渐增加，使狭管风力机在约9.60 m/s的风速下即可达到设计11.50 m/s才能达到的2 MW额定功率。

3)Wilson叶片建模法总体来说考虑比较全面，模型输出功率符合预期，但由于考虑到实际情况仿真时并未将叶片设成光滑表面，且Wilson方法未考虑轮毂损失、尾流损失因子、叶轮受塔架回流等因素的影响，使同风速下平地风力机功率比理论值稍低。

4)狭管区域收缩段对流体加速效果明显，但风力机后部的整体流场明显比单机时复杂得多，且影响距离与两座山体的外形密切相关，由于扰流等因素将产生多条高速与低速尾流带，彼此相互影响。在选择狭管区域与进行风力机排布时，需充分考虑尾流发展的情况。

[1] 沈晶, 赖旭. 峡谷地形条件下风电场风况数值模拟研究[J].水电能源科学, 2011, 29(8): 167-171.

[2] 庞加斌. 沿海和山区强风特性的观测分析与风洞模拟研究[D]. 上海: 同济大学, 2006.

[3] 郭文星. 复杂山地地形风场 CFD 多尺度数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[4] Michel Make, Guilherme Vaz. Analyzing scaling effects on offsho-re wind turbines using CFD[J]. Renewable Energy, 2015, (83): 1326-1340.

[5] 陈洁鹰. 2MW风力机叶片优化设计及其关键性能仿真研究[D]. 沈阳: 东北大学, 2012.

[6] Carrión M, Steijl R, Woodgate M, et al. Aeroelastic analysis of wind turbines using a tightly coupled CFD–CSD method[J]. Journal of Fluids and Structures, 2014, (50): 392-415.

[7] Alexandros Makridisn, John Chick. Validation of a CFD model of wind turbine wakes with terrain effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, (123): 12-29.

[8] 李少华, 王东华, 岳巍澎, 等. 双风力机风向变化时尾流及阵列数值研究[J]. 动力工程学报, 2011, 31(10): 768-778.

[9] 汪泉. 风力机叶片气动外形与结构的参数化耦合设计理论研究[D]. 重庆: 重庆大学, 2013.

[10] Francesco Balduzzi, Alessandro Bianchini, Riccardo Maleci, et al. Critical issues in the CFD simulation of Darrieus wind turbines[J]. Renewable Energy, 2016, (85): 419-435.

[11] Young-Tae Lee, Hee-Chang Lim. Numerical study of the aerody-namic performance of a 500W Darrieus-type vertical-axis wind turbine[J]. Renewable Energy, 2015, (83): 407-415.

[12] Abdullah Mobin Chowdhury, Hiromichi Akimoto, Yutaka Hara-M. Comparative CFD analysis of vertical axis wind turbine in upright and tilted configuration[J]. Renewable Energy, 2016, (85): 327-337.

[13] Juliana B R Loureiro, Alexandre T P Alho, Atila P Silva Freire. The numerical computation of near wall turbulent flow over a steep hill[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(5): 540-561.

[14] Li Y, Castro A M, Sinokrot T, et al. Coupled multi-body dynamics and CFD for wind turbine simulation including explicit wind turbulence[J]. Renewable Energy, 2015, (76): 338-361.

2016-03-11

可再生能源电力技术湖南省重点实验室(长沙理工大学)开放基金资助项目(2012ZNDL008）

庞博( 1991—)，男，硕士研究生，主要从事风能资源评估，风力机发电、计算机仿真与优化，热工设备检测与热工计算方面的研究。cspangbo@163.com