基于沥青混合料细观结构的劈裂试验数值模拟
陈斯宁,赵俊明,陈红斌
(1.宿迁市高速公路建设指挥部,江苏 宿迁 223800; 2.苏交科集团股份有限公司,江苏 南京 210017)
基于沥青混合料细观结构的劈裂试验数值模拟
陈斯宁1,赵俊明2,陈红斌2
(1.宿迁市高速公路建设指挥部,江苏 宿迁 223800; 2.苏交科集团股份有限公司,江苏 南京 210017)
为了分析非均质性对沥青混合料劈裂试验的影响,文章基于沥青混合料CT扫描图像,利用数字图像处理技术获取细观几何结构信息,结合推进波前法(Advancing Front Technique,AFT)网格剖分技术生成沥青混合料细观网格模型,进一步进行材料属性定义、边界条件约束和加载来模拟劈裂试验过程。从时间和空间角度剖析了沥青混合料细观结构的应力应变分布规律,研究结果表明:随着加载时间的增加,水平应力应变、竖向应力应变和剪切应力应变均以不同的速率逐渐增加,竖向应力应变大于水平应力应变,剪切应力应变最小;整体上,应力应变在竖向两端处最大,中心位置处次之,水平两端处最小;竖向两端处和中心位置最容易出现裂缝。
沥青混合料;细观结构;有限元法;劈裂试验
1 概述
沥青混合料作为一种多组分构成的复合材料,可视为大量的粗集料和空隙分散于沥青砂浆中。由于各组分体积比、性质、几何特征和空间分布特征等细观结构特征的不同,导致沥青混合料力学特性极其复杂。劈裂试验作为一种评价物质劈裂破坏时性能的手段,可用于测定沥青混合料在规定温度和加载速率下劈裂破坏时的力学性能[1]。然而,仅仅通过劈裂试验无法获得沥青混合料试件的内部力学响应。因此,在劈裂试验的加载过程中,如何从细观角度评价沥青混合料内部力学响应是一个亟需解决的问题。
国内学者大多数利用CT扫描技术和数字图像处理技术生成数值模型,通过模拟劈裂试验的全过程分析沥青混合料的力学响应。皮育晖等[2]人利用ABAQUS有限元软件对沥青混合料劈裂试验进行二维和三维数值模拟对比,发现网格划分密度、划分形式对有限元模拟结果有较大影响;对于不同的沥青混合料,其劈裂试验模拟应以相应材料的单轴抗压试验结果为材料特性进行定义;通过三维模拟及理论对比验证,发现在一定条件下利用简化的二维模型是可行的。邱延峻等[3]人通过模拟劈裂试验得出,裂纹状态随均质度的减小趋向离散,高均质度的试件劈裂裂纹状态更具有规则;受非均质基元体随机分布的影响,试件劈裂过程中的应力分布呈现出多峰值现象;马歇尔试件的数值试验和物理试验具有相同的劈裂过程。闫超[4]利用ANSYS有限元软件模拟了平面应变和三维沥青混合料的劈裂试验,提出了模型在不同切割宽度下劈裂强度的计算公式,并进一步尝试模拟黏弹性条件下沥青混合料的劈裂试验。王端宜等[5]考虑了沥青混合料内部分布的不均匀性,利用CT扫描技术和数字图像处理技术构建沥青混合料数值模型,讨论分析了沥青混合料内部不均匀分布、级配类型、模量比、有无空隙及加载位置对劈裂试验模拟结果的影响。杨继康等[6]基于数字图像处理技术,利用有限元方法进行细观力学分析,最后得出水平拉应变集中出现在沥青砂浆相且沿边界面传递,砂浆与界面处为抗拉薄弱区。
综上所述,对于沥青混合料的劈裂试验,采用CT扫描技术-数字图像处理技术-有限元方法能够很好地将沥青混合料细观结构力学响应与宏观力学性能结合起来,因此,本文利用CT扫描技术获得沥青混合料图像特征信息,利用数字图像处理技术获取细观几何结构信息,利用有限元方法模拟劈裂试验过程,讨论分析了不同加载时间不同空间位置的应力和应变变化规律。
2 沥青混合料劈裂试验有限元模拟建模
2.1 几何模型
鉴于劈裂试验中试件尺寸要求,本文采用标准马歇尔试件进行劈裂试验数值模拟,即试件直径为101.6 mm,压头宽度为12.7 mm,压头内表面与试件进行完全粘合。将沥青混合料视为粗集料和沥青砂浆组成的二相混合物,为了生成沥青混合料细观有限元模型,首先需要识别和提取各组分的细观结构特征,具体步骤如下:
(1)利用工业CT扫描沥青混合料试件获取图像,并利用数字图像处理技术进行图像处理,比如图像增强、噪声消除等操作,根据双峰法确定分割阈值,提取粗集料坐标点信息,剩余部分视为沥青砂浆组分;
(2)根据提取的粗集料坐标点信息,通过实际尺寸单位和像素单位之间的转化、粗集料颗粒编号、边界简化及布尔运算等处理,从而生成沥青混合料细观几何模型,几何信息包括粗集料颗粒边缘坐标及试件外围坐标。
2.2 材料模型
参考相关的文献资料[7],本文采用的玄武岩集料视为线弹性材料[8],将沥青砂浆视为黏弹性材料,鉴于Burgers模型可以较好表征沥青砂浆中温及低温状况下短期应力应变特性,综合考虑后选取Burgers模型来描述其行为特征。本文根据室内单轴压缩蠕变试验结果,通过对试验数据进行拟合得到Burgers模型四参数,并转换成prony级数形式用于后期模拟计算。在模拟中,不考虑集料和沥青砂浆之间的接触问题,上下压头为刚体,并与沥青混合料形成一个连续的整体。沥青混合料各组分材料参数如表1所示。

表1 沥青混合料各组分材料参数
2.3 网格剖分及边界条件
将沥青混合料视为粗集料和沥青砂浆组成的二相混合物,在识别和提取各组分的细观结构特征后,需要根据几何结构特征进行网格剖分。目前,常规的网格剖分方法有自由网格剖分、栅格网格剖分、推进波前法(Advancing Front Technique ,AFT)网格剖分等[9]。自由网格剖分是将几何模型直接导入通用有限元软件中,根据一个网格尺寸大小来控制网格数量,直接对几何模型进行网格剖分,该方法可以较快地生成网格,但其网格质量与几何形状、网格数量、自由划分算法等有关,对于沥青混合料细观结构具有一定的局限性。栅格网格剖分是将沥青混合料截面中每个像素作为一个网格,其适用于任何复杂几何形状的网格剖分,但其网格质量受CT扫描图像质量的影响,且网格边界单元质量差。推进波前法是从待剖分区域的边界开始的,由边界构成初始前沿队列,每次生成一个单元向未生成网格的区域内部推进,直至整个区域完全被单元覆盖为止,是一种较好的非结构化有限元网格剖分方法。本文考虑沥青混合料细观结构特点,采用推进波前法进行网格剖分,具体步骤如下:
(1)考虑沥青混合料细观几何模型特点,首先提取沥青混合料中粗集料的闭合边界坐标以及沥青混合料外边界坐标,作为初始前沿队列;然后基于初始前沿队列逐个生成单元向未生成网格的区域内部推进,直至整个区域完全被单元覆盖为止,沥青混合料细观网格模型如图1所示。

图1 沥青混合料细观网格模型
(2)通过直接建模方法,将细观网格模型导入有限元软件中,并设置材料属性,构建沥青混合料细观有限元模型,用于细观力学分析。
在进行加载时,可以采用力加载模式或位移加载模式,考虑劈裂试验的实际加载过程,本文采用顶部竖向加载方式,施加1 mm竖向位移,加载速率为10 mm/min,其底部竖向约束。
3 试验结果与分析
3.1 不同加载时间下的应力和应变变化规律分析
不同加载时间下沥青混合料劈裂细观有限元模型中心点处的应力应变变化曲线如图2所示。
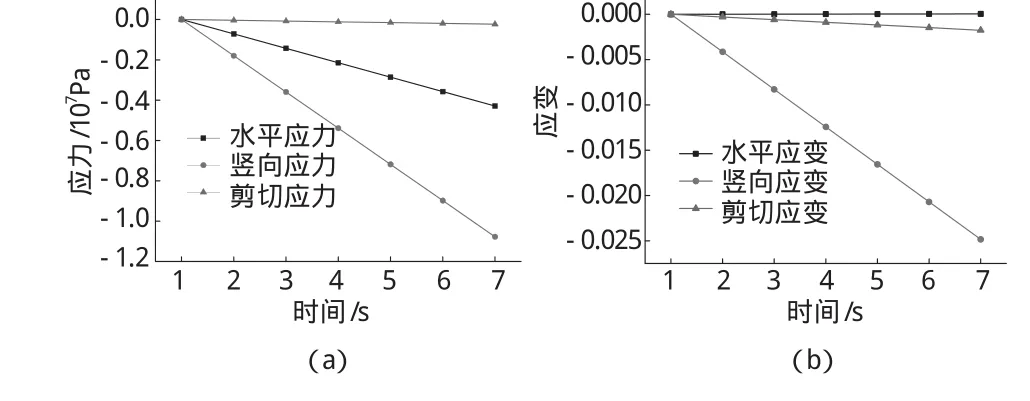
图2 应力和应变随加载时间的变化曲线(顶点处)
由图2可以看出,对于应力来说,随着时间的增加,水平应力、竖向应力和剪切应力均以不同的速率逐渐增加,负号代表应力的方向;增长速度最快的是竖向应力,其次是水平应力,增长速度最慢的是剪切应力;在最大时间点,竖向应力达到11 MPa,水平应力达到4 MPa,相对而言,剪切应力几乎没有太大变化。由此可以推断出,在荷载作用下,竖向应力敏感性最强,其次为水平应力,而剪切应力的敏感性最差,几乎没有变化。对于应变来说,随着时间的增加,水平应变、竖向应变和剪切应变亦在逐渐增加,但是应变的变化规律和应力相比则不同。可以发现,竖向应变的变化规律和竖向应力是相同的,且变化程度相对于水平应变和剪切应变都比较大;和应力变化不同,剪切应变的变化速度则是大于水平应变,这点和应力相反,应力的变化是水平应力变化速度大于剪切应力变化速度。在最大时间点,竖向应变已经达到-0.025,剪切应变却只有-0.002,水平应变则更小。
3.2 不同空间位置的应力和应变变化规律分析
在2 s时间点处,沥青混合料劈裂细观有限元模型不同空间位置的应力云图如图3所示,应变云图如图4所示。

图3 应力云图(2 s时刻)

图4 应变云图(2 s时刻)
由图3可以看出,在2 s时刻,水平应力云图的最大压应力为7.72 MPa,其位置出现在试件接近压头的部位,试件沿中垂线方向压应力逐渐减小,甚至中间有几部分出现拉应力,试件左右两端则是标准受压状态,压应力数值可达0.7 MPa左右。水平应力的最大拉应力为7.98 MPa,这一数值比最大压应力的数值还要大;水平应力呈水平带状分布,且砂浆和粗集料均产生不均匀分布;竖向压应力云图的最大压应力为8.72 MPa,可以看出在压头上下区域都有条纹达到最大压应力,沿着试件中垂线劈裂状态下的压应力逐渐减小,但是在试件水平方向,压应力是逐渐在减小,但仍然处于受压状态,其数值可达0.5 MPa左右。竖向应力的最大拉应力为5.98 MPa,相对于最大压应力小的多,这一现象和水平应力相比则不同。竖向应力沿粗集料边界呈竖向带状分布,且砂浆区域的竖向应力相对分布均匀;剪切应力云图的最大压应力为5.72 MPa,可以看出在压头下方的区域,此时的受力比较复杂,同时有最大和最小应力出现,但是在试件水平方向仍然是处于压应力状态,这一现象和水平应力以及竖向应力都有不同,且其最大值均比水平应力和竖向应力要小。剪切应力呈两端沿粗集料长轴方向斜向分布,且在粗集料中呈不均匀分布。
由图4可以看出,在2 s时刻,水平应变沿中垂线方向呈现的是受压状态,其最大应变值为0.009 067在水平方向呈现受拉状态,其应变值约为- 0.001 302其中试件的最大受压应变为- 0.009 598,对比可以发现最大压应变的数值要比最大拉应变的要大,但相差并不是太大;由竖向应变的云图可以看出,试件的水平方向大部分区域都是处于压应变的状态,在压头附近出现最大压应变的区域,最大值为0.002,但是在试件沿中垂线方向,则是出于受拉应变状态,其值最大为-0.015。在竖向应变云图中,其压应变的最大值要小于拉应变的最大值,这一现象和水平应变云图相比是相同的,并且在竖向应变中,拉应变的最大值是压应变的最大值的7.5倍;由剪切应变云图可以看出,在压头附近同时出现了最大最小值,这一现象和剪切应力云图类似,最大拉应变为-0.015,最大压应变为0.01,同样也是最大拉应变的数值要比最大压应变的要大,但是相对于竖向应变而言,其大小差距程度要小的多。
在2 s时间点处,沥青混合料劈裂细观有限元模型应力和应变沿水平方向的变化曲线如图5所示,应力和应变沿竖向的变化曲线如图6所示。

图5 应力和应变沿水平方向的变化曲线

图6 应力和应变沿竖向的变化曲线
由图5可以看出,整体上,3种应力的变化有一定的相关性,其中竖向应力在数值上大于水平应力和剪切应力,对于竖向应力,随着距左边顶点距离的增加,呈先增加后减小的趋势,受沥青混合料非均质的影响,其应力大小出现波动变化规律,一定程度上反映了集料和沥青砂浆的不均匀分布对应力分布的影响;此外,在试件水平方向端点处的应力数值较小,中心位置较大,且峰值一般出现在沥青砂浆和集料的界面处;水平应力和剪切应力数值随着距左顶点的距离变化而变化,但变化幅值较小;对于应变而言,其变化规律与应力类似,竖向应变在数值上仍然是大于水平应变和剪切应变,对于竖向应变,随着距左边顶点距离的增加,呈先增加后减小的趋势,受沥青混合料非均质的影响,其应变大小也出现波动变化规律;此外,在试件水平方向端点处的应变数值较小,中心位置较大,且在端点处出现了竖向应变小于水平应变和剪切应变的情况。
综上分析可以看出,应力应变在水平方向两端处较小、中心位置处较大,中心位置相比水平方向两端位置更容易出现裂缝。
由图6可以看出,与水平方向的应力应变变化曲线类似,整体上,3种应力的变化是有一定的相关性的,其中竖向应力在数值上仍然是大于水平应力和剪切应力,对于竖向应力,随着距上顶点距离的增加,呈先减小后增加的趋势,受沥青混合料非均质的影响,其应力大小出现波动变化规律;此外,在试件竖向端点处的应力数值较大,中心位置较小,且峰值一般出现在沥青砂浆和集料的界面处;水平应力和剪切应力的大小则随着距上顶点的距离的变化而变化,但变化幅值较小。对于应变而言,整体上,竖向应变数值大于水平应变和剪切应变,三者在集料区域变化较大,而在沥青砂浆区域变化较小,且竖向应变均为负值,而水平应变和剪切应变均为正值。
综上分析可以看出,应力应变在竖向两端处较大、中心位置处较小。竖向两端位置相比中心位置更容易出现裂缝。
4 结论
针对非均质条件下沥青混合料劈裂试验数值模拟问题,本文基于沥青混合料CT扫描图像,利用数字图像处理技术和有限元数值模拟技术,分析劈裂试验过程中沥青混合料内部应力应变的时空分布规律,具体结论如下:
(1)随着加载时间的增加,各方向应力应变逐渐增加,其中竖向最大,应力达11 MPa,应变达-0.025;剪切最小;
(2)水平方向上,应力应变在水平方向两端处较小、中心位置处较大;竖向方向上,应力应变在竖向两端处较大、中心位置处较小;相比水平两端位置,竖向两端位置最容易出现裂缝,其次是中心位置、水平方向。
[1]JTJ052—2000公路工程沥青及沥青混合料试验规程[S].
[2]皮育晖,张久鹏,黄晓明,等.沥青混合料劈裂试验数值模[1]拟[J].公路交通科技,2007,24(8):1-6.
[3]邱延峻,闫常赫,艾长发.非均质沥青混合料劈裂试验全过[1]程数值模拟[J].交通运输工程学报,2009,9(2):12-16.
[4]闫超. 沥青混合料间接拉伸试验的弹粘性分析[D].西安:[1]长安大学,2010.
[5]王端宜,吴文亮,张肖宁,等.基于数字图像处理和有限元建模方法的沥青混合料劈裂试验数值模拟[J].吉林大学[1]学报,2011,41(4):968-973.
[6]杨继康,王晓川.沥青混合料劈裂试验的细观模拟验证与[1]分析[J].中外公路,2015,35(2):230-233.
[7]汪海年.沥青混合料微细结构及其数值仿真研究[D].西[1]安:长安大学,2007.
[8]Kose,S.,Guler,M.,Bahia,H. U. Distribution of strains within [1]asphalt binders in HMA using imaging and finite element [1]techniques[C]∥TRB,2000.
[9]古成中,吴新跃.有限元网格划分及发展趋势[J].计算机[1]科学与探索,2008,2(3):248-259.
Numerical Simulation of Spli Test Based on Microstructure of Asphalt Mixture
Chen Sining1, Zhao Junming2, Chen Hongbin2
(1.Expressway Construction Headquarters of Suqian City, Suqian 223800, China; 2. JSTI Group, Nanjing 210017, China)
In order to analyze the influence of heterogeneity on asphalt mixture split test, a microscopic finite element (FE) modeling of asphalt mixtures was obtained base on CT computed technique, digital image processing and finite element method. Firstly, the geometry information of microstructure was identified by digital image processing. Secondly, mesh model of microstructure was generated with advancing front technique (AFT). Finally, the material properties, boundary conditions and loading were used to simulate the process of splitting test, and the stress and strain distributions of the asphalt mixture were analyzed from the perspective of time and space. The results indicated that horizontal stress strain, vertical stress strain and shear stress strain increased gradually with the increase of the loading time, and vertical stress strain was greater than horizontal stress strain, while shear stress strain was the smallest; on the whole, the stress and strain in the vertical ends was the biggest, the center position was second, the horizontal ends was the smallest; the vertical ends and the center position were the most easily cracking. Key words: asphalt mixture; microstructure; finite element method; split test
U414
A
1672-9889(2016)04-0011-05
陈斯宁(1969-),男,江苏宿迁人,高级工程师,主要从事高速公路建设和管理工作。
2015-09-30)

