非圆锥齿轮的设计及运动学仿真
李文长,贾巨民,张学玲
(1.军事交通学院 研究生管理大队,天津 300161;2.军事交通学院 军事物流系,天津 300161)
● 基础科学与技术Basic Science & Technology
非圆锥齿轮的设计及运动学仿真
李文长1,贾巨民2,张学玲2
(1.军事交通学院 研究生管理大队,天津 300161;2.军事交通学院 军事物流系,天津 300161)
为提高变传动比差速器的锁紧系数,基于保测地曲率映射的非圆锥齿轮设计方法,提出一种非圆锥齿轮的传动比规律,设计该非圆锥齿轮,建立三维模型,对非圆锥齿轮的传动进行运动学仿真。将仿真数据与理论计算结果进行对比,验证了理论设计方法及其模型建立的正确性。
非圆锥齿轮设计;运动仿真;误差分析
非圆锥齿轮综合了非圆齿轮与圆锥齿轮的特性,既能够实现相交轴之间的传动,又能够实现变速比传动。对称安装的非圆锥齿轮具有结构紧凑、传动平稳、传动效率高且易实现动平衡等优点[1]。非圆锥齿轮作为一种新型的齿轮传动形式,目前尚无成熟的理论和方法来指导非圆锥齿轮的设计。林超等[1]基于传统的齿轮范成法原理,对高阶椭圆锥齿轮的设计计算方法进行了研究;姜虹等[2]提出了一种非圆锥齿轮的当量设计方法;贾巨民等[3]提出了一种利用保测地曲率映射的方法将非圆锥齿轮球面节曲线映射到平面,将空间啮合问题转换为平面问题,给出了齿形的设计计算方法。这些研究成果对非圆锥齿轮的设计制造与推广应用提供了途径,但是由于非圆锥齿轮结构的复杂性,均未对所设计的非圆锥齿轮运动规律作详细分析研究。
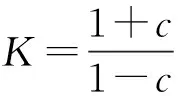
1 非圆锥齿轮设计
1.1传动比变化规律和节曲线设计
对于如图1所示的一对锥齿轮传动,当齿轮副的轴间夹角之和∑=δ1+δ2=90°,传动比为
(1)
式中:φ1、φ2分别为主动齿轮与从动齿轮转角;δ1、δ2分别为主动齿轮与从动齿轮节锥角。
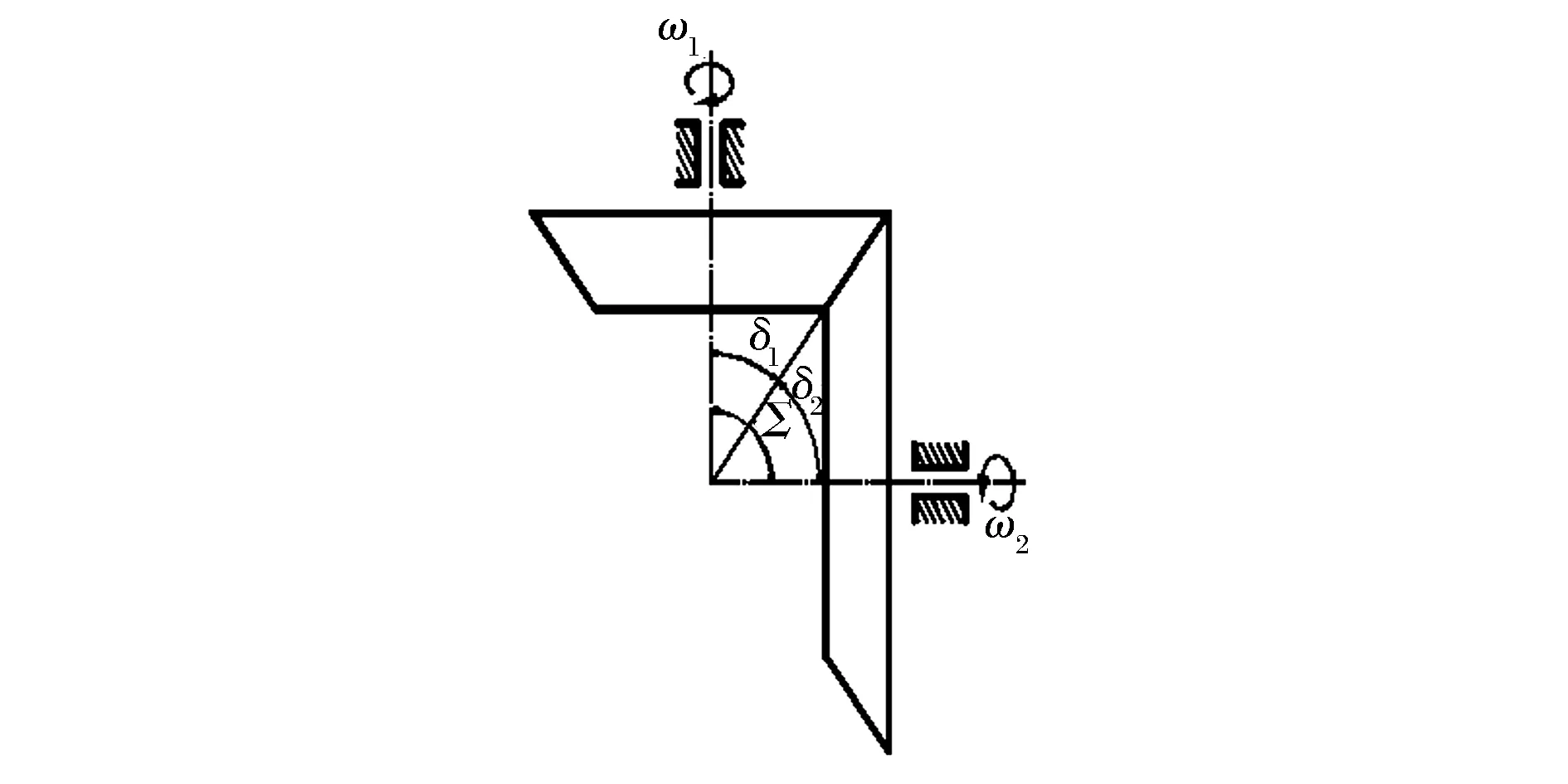
图1 一对锥齿轮传动示意
对于非圆锥齿轮来说,两个齿轮的节锥角δ1、δ2不再是定值,而是关于两个传动齿轮转角φ1或φ2的函数。
正弦曲线运动规律的加速度规律为余弦规律,加速度曲线连续。由齿轮传动理论,传动比函数为周期函数,既保证节曲线的封闭,又使传动比周期性变化,同时余弦加速度规律减小了冲击。因此,本文选用传动比规律为
(2)
根据几何关系,齿轮1,2的球面节曲线可分别表示为
(3)
式中R为球面半径。
根据式(1)和式(2),可得到非圆锥齿轮的δ1、δ2、φ2关于φ1的函数关系为
代入式(3)即为以φ1为参数的球面节曲线方程。
1.2节曲线平面映射
根据微分几何曲面论的基本定理[2],若曲面Σ上一条曲线Γ在平面上π展开为平面曲线Γ*,则Γ在曲面上的测地曲率κg等于Γ*在平面上的相对曲率κr,即
κg=κr
(4)
结合平面曲线论的唯一存在定理[4],已给一个闭区间[s0,s1]里的连续函数kr(s),平面曲线上的一个点(x0,y0),和一个矢量a=icosψ0+jsinψ0,有且仅有一条平面有向曲线为
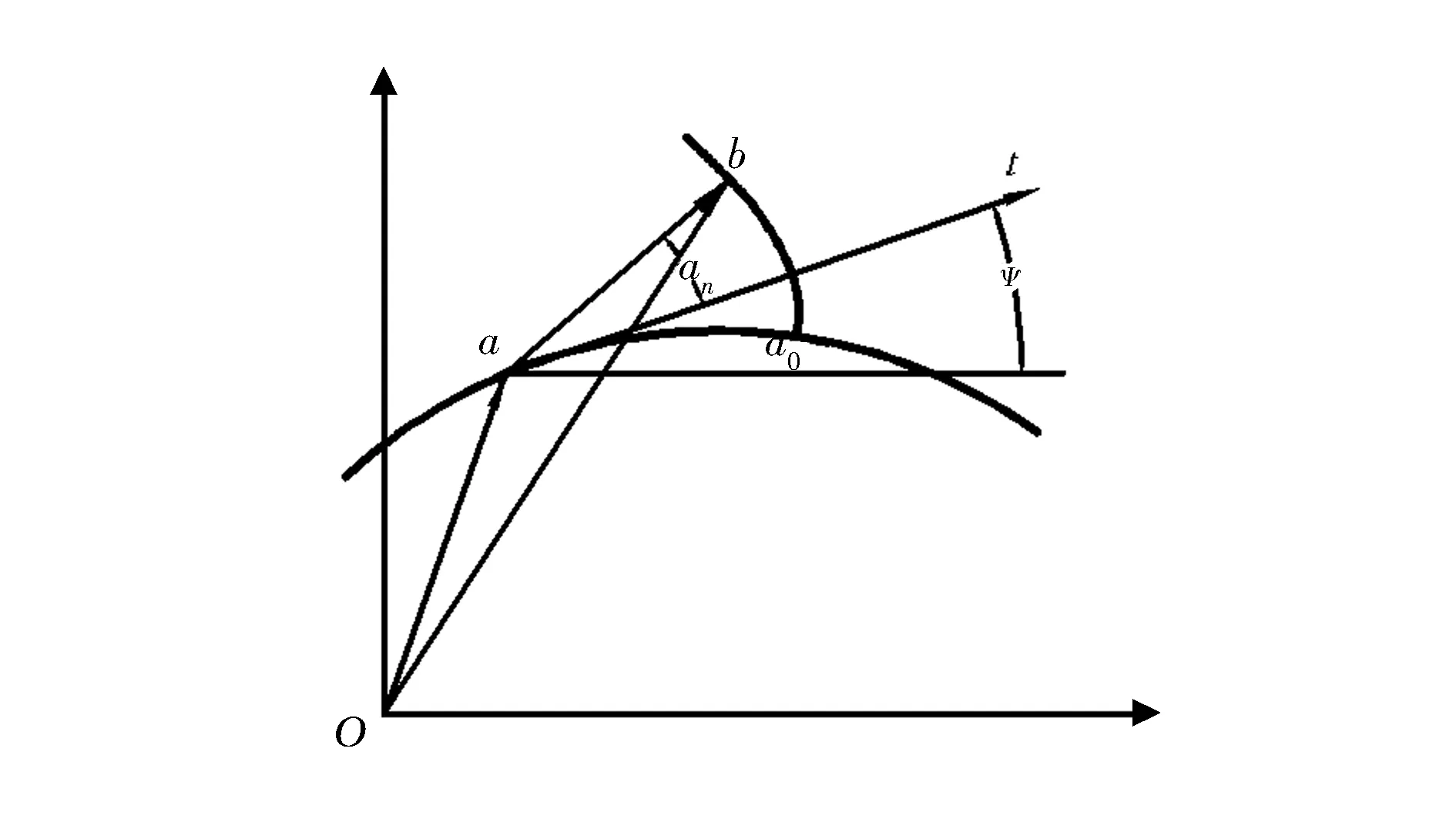
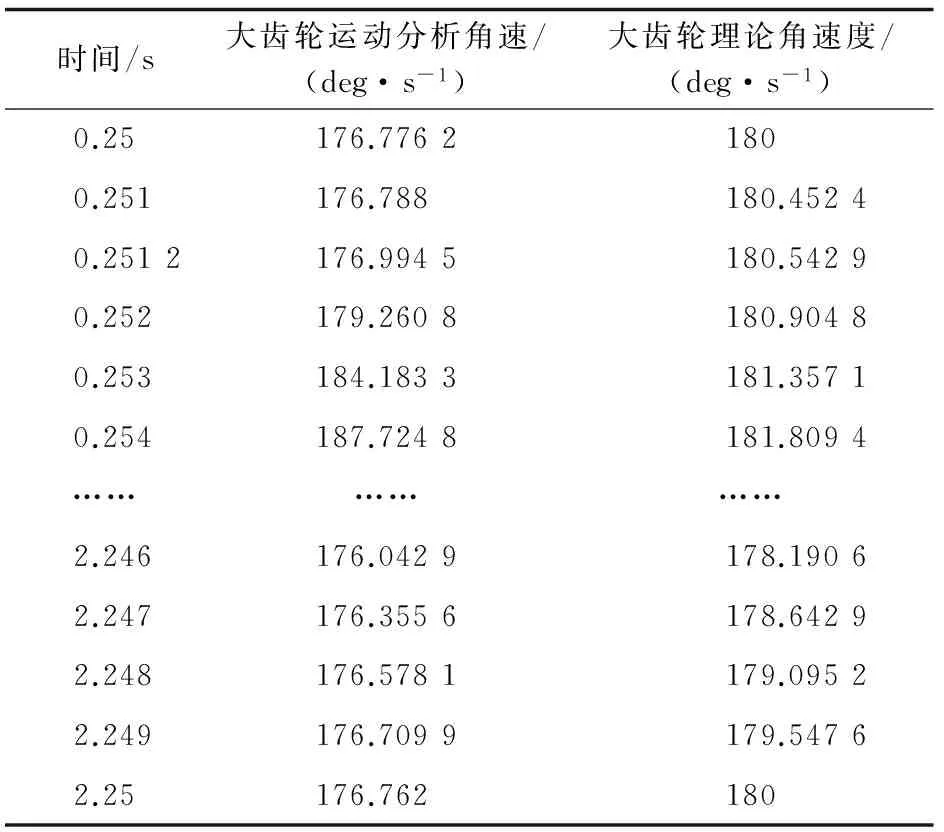
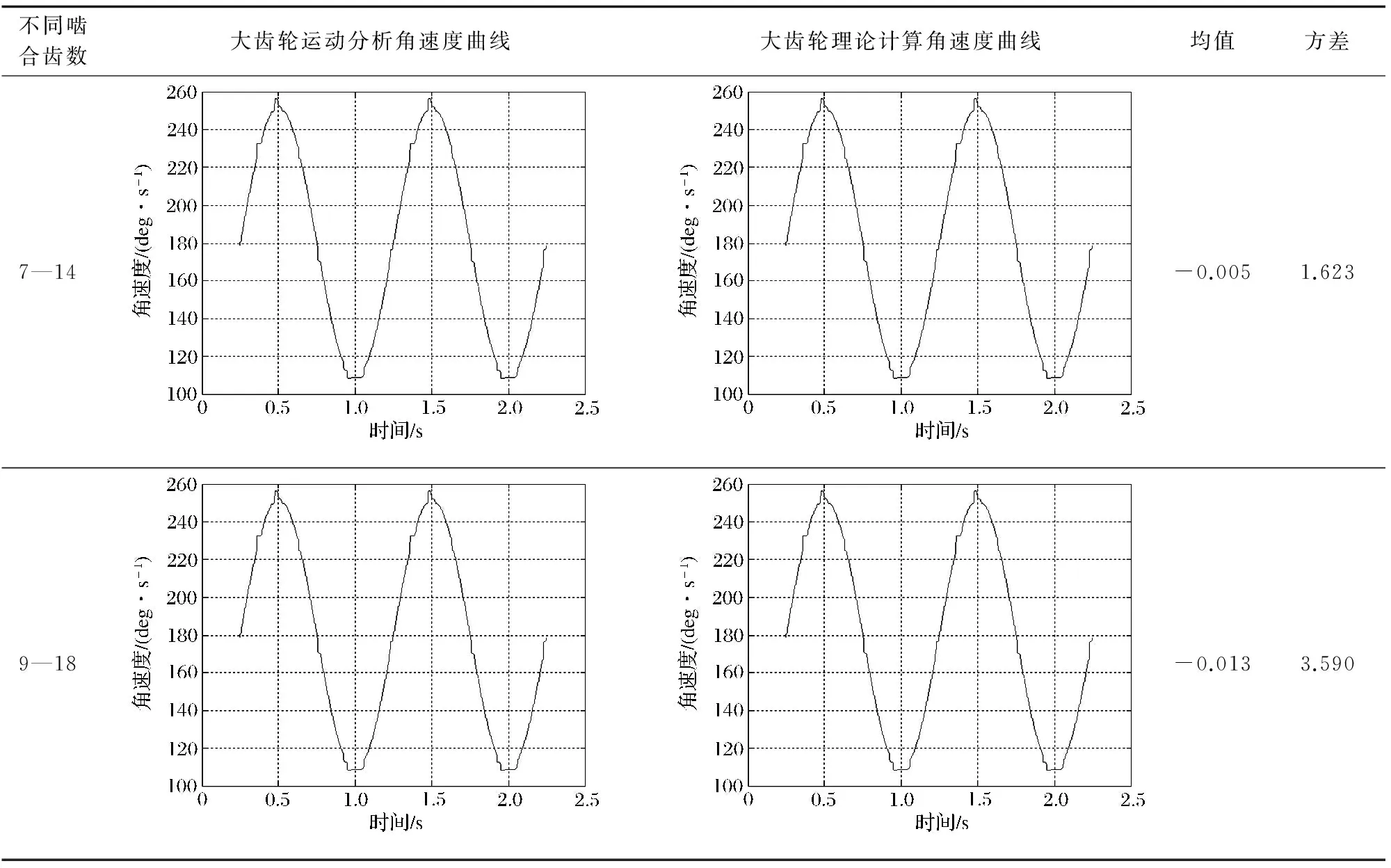
r=x(s)i+y(s)js0 (5) 因此,只要给出曲面上一条曲线的测地曲率以及初始条件,就可以唯一确定一条平面展开曲线,映射后得到平面曲线为 (6) 式中s0、s1、ψ0、x0、y0由边界条件确定。 对于本文实例,按上述方法求出其平面映射节曲线如图2所示,非圆锥齿轮副的啮合传动相当于图2中节曲线的纯滚动。 图2 球面节曲线在平面上伸展—映射节曲线 1.3平面齿形设计 通过解析法直接由节曲线方程推导齿形方程,根据基本啮合原理[5],采用渐开线齿形为例进行说明。如图3所示,以节曲线上的右齿形为例,则齿形上任意一点b的方程可写为[6] rb=ra+Iab (7) 式中:ra为节曲线a点处的矢径;Iab为齿形上b点的法矢量。 根据齿形法线法原理(如图3所示),有 Iab=a0acosαn=scosαn (8) 式中αn为齿条刀具齿形角。 图3 齿形计算原理 (9) 同理,可得出左齿形方程 (9) 根据以上公式,以当量齿轮节曲线为基础,就可以借助平面啮合原理进行非圆锥齿轮传动的齿形分析和设计。 1.4非圆锥齿轮模型创建 给定齿厚、顶圆高和齿根高,结合数学软件,根据设计理论编制数学程序,计算锥齿轮的齿廓坐标,将齿廓坐标计算结果导入Solidworks软件中,利用轮廓数据点生成样条曲线来创建齿轮齿廓,生成非圆齿轮三维模型。用上述方法设计的非圆锥齿轮对如图4所示,齿数分别为7、14。同理设计齿数分别为9、18的齿轮对。 图4 7—14齿非圆锥齿轮对 为检验所设计非圆锥齿轮对的运动情况,检查其齿形能否正确啮合,以及两个齿轮能否提供预设的传动比,要对其三维模型进行干涉检查和运动学仿真。 2.1仿真分析方法 将设计的大小两个非圆锥齿轮进行配合,创建非圆锥齿轮装配仿真模型(如图4所示)。小齿轮为主动齿轮,绕其固定轴线转动,通过齿轮间的啮合,将运动传递给大齿轮,大齿轮绕其轴线转动。 进入SolidWorks Motion分析环境,选取两个模型,对装配好的两个齿轮进行接触的定义[7-9]。定义伺服电动机,选择小齿轮的连接轴作为伺服电动机的驱动对象,并且规定电动机的转动方向,设定小齿轮的当前位置为初始位置,定义伺服电动机的速度为常数“60 r/min”。 最后,对运动分析属性进行设置,运动帧数设置1 000,接触精度0.000 000 001,高级设置中设置解算器WISTIFF,以获得足够的运动数据,保证运动分析数据的精确性。 2.3运动分析数据获取 运动分析后,可得大齿轮运动仿真速度数据,取极限位置为起始点,一个周期的数据分析。部分数据见表1。 2.4误差计算及分析 设计不同齿数的非圆锥齿轮进行配合,分别设计7齿与14齿、9齿与18齿两组齿轮进行啮合运动仿真。小齿轮转速n1=360 deg/s,代入传动比设计规律式(2),则大齿轮的理论角速度为n2t=n1i12=360×i12。 表1 齿轮运动仿真速度数据与理论角速度 对于数据采集点j处,其理论速度与仿真分析角速度差为 Δnj=n2t-n2 (10) 则角速度差的均值为 (11) 则角速度差的方差为 (12) 对角速度差数据处理,计算其均值和方差。去除运动仿真时啮合机构运行的启动阶段数据,速度曲线及计算结果见表2。 从7—14齿齿轮对模型计算结果可以看出,仿真速度曲线与理论设计曲线相吻合,速度差值较小,由方差可以看出理论与分析速度差变化幅度小,运动相对稳定。 表2 大齿轮理论与仿真分析计算结果 设计9—18齿齿轮对模型,与7—14齿齿轮对模型进行对比,由于齿数的增加,啮合传动更加充分,速度差的均值变小,其方差也变小,运动更平稳。两组模型的均值和方差计算结果都较小,在合理范围内,表明非圆锥齿轮的设计计算、模型建立以及仿真方法的正确性。 但从两组模型的仿真速度曲线可以看到,在靠近速度最大与最小的极限位置,速度波动程度相对较大,出现小幅度速度突变。以7—14齿齿轮对为例,速度突变处对应的极限位置分别如图5、图6所示。 图5 极限位置1 图6 极限位置2 节曲线的设计在理论上是处处光滑的,极限位置1、2处既是传动比变化最大处,也是节曲线变化最大处,该位置出现速度曲线突变的原因,一方面是该处曲线齿廓曲线精度较低,另一方面齿廓曲线采用数值方法来设计,必然存在一定误差,这也是未来需要深入研究之处。 通过分析可知:齿数增加可以减小误差,但齿数增加同时减小轮齿的“模数”,从而减小抗弯强度,这是实际的一个矛盾点;另一方面,减小锁紧系数可以减小误差,这与设计期望相矛盾。综合考虑,设计参数合理,且在工程误差允许范围内。 本文基于保测地曲率映射的非圆锥齿轮传动设计分析方法,提出新的传动比规律,设计非圆锥齿轮,提高锁紧系数。设计两组不同齿数的配合齿轮对,分别进行运动仿真以及误差分析,均值和方差计算结果都在合理范围内;分析了最大误差位置及误差产生的主要原因,齿数增加可以减小误差,使运动更平稳,增大锁紧系数会增大误差。所设计齿轮能实现预期的运动特性,为非圆锥齿轮的设计和制造提供了参考方法和理论依据。 [1]林超,龚海,侯玉杰,等.高阶椭圆锥齿轮齿形设计与加工[J].中国机械工程,2012,23(3):253-254. [2]姜虹,王小椿. 三周节变传动比限滑差速器设计与实验[J]. 农业机械学报,2007,38(4):31-34. [3]贾巨民,高波,赵德龙.基于保测地曲率映射的非圆锥齿轮传动设计分析方法[J].机械工程学报,2008,44(4):53-57. [4]吴大任. 微分几何学讲义[M].北京:人民教育出版社,1982:222-225. [5]李福生,尹种芳,张遵连,等.非圆齿轮与特种齿轮传动设计[M].北京:机械工业出版社,1983:111-117. [6]贾巨民,高波,索文莉,等.越野汽车新型变速比差速器的研究[J].中国机械工程,2012,23(23):2845-2846. [7]顾婷婷.槽轮机构在SolidWorks中的建模装配与运动分析[J]. 机械工程与自动化,2007,142(3):144-145. [8]柴树峰,张学玲,李玉兰.非圆齿轮设计及运动学仿真分析[J].军事交通学院学报,2014,16(9):36-40. [9]林超,侯玉杰,冉小虎,等.高阶椭圆锥齿轮的传动模型与干涉检查的运动仿真[J].重庆大学学报,2010,33(10):4-5. (编辑:史海英) Design and Kinematic Simulation of Noncircular Bevel Gears LI Wenchang1, JIA Jumin2, ZHANG Xueling2 (1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161,China;2.Military Logistics Department, Military Transportation University, Tianjin 300161,China) To improve the locking coefficients of variable ratio differentials, by using preserved geodesic curvature designing method, this paper presents the laws of transmission ratio, comes up with a new design of noncircular bevel gear and builds a 3-Dimentional model by which kinematical simulation are carried out with the transmission of this gear. The comparison between the data obtained from the kinematic simulation and the results of the theoretical calculation verifies the method and the model. noncircular bevel gear; kinematic simulation; error analysis 2015-10-15; 2015-11-13. 天津市应用基础与前沿技术研究计划项目(12JC2DJC34600). 李文长(1992—),男,硕士研究生; 贾巨民(1965—),男,博士,教授,硕士研究生导师. 10.16807/j.cnki.12-1372/e.2016.07.021 TH132.4 A 1674-2192(2016)07- 0091- 05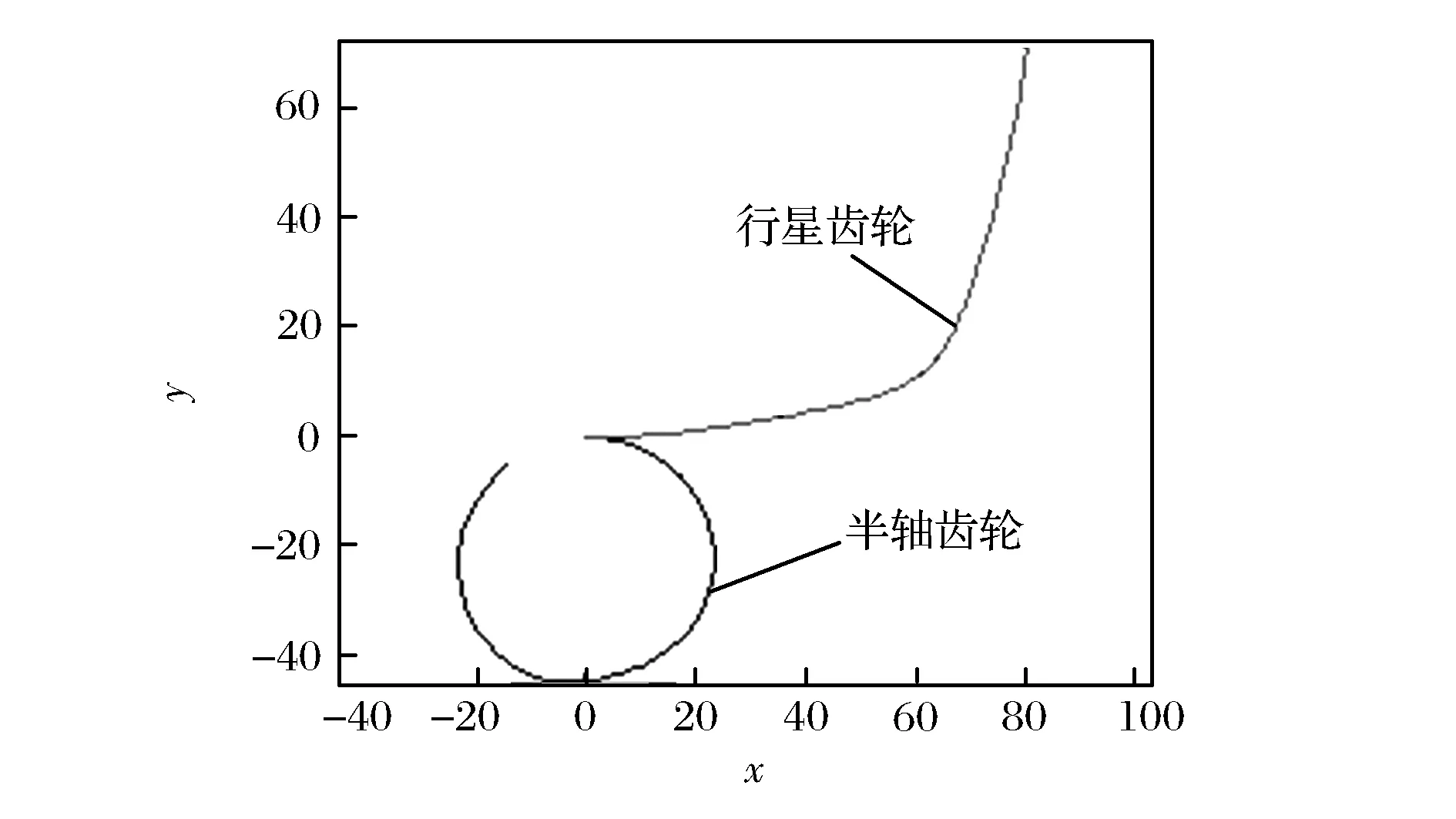
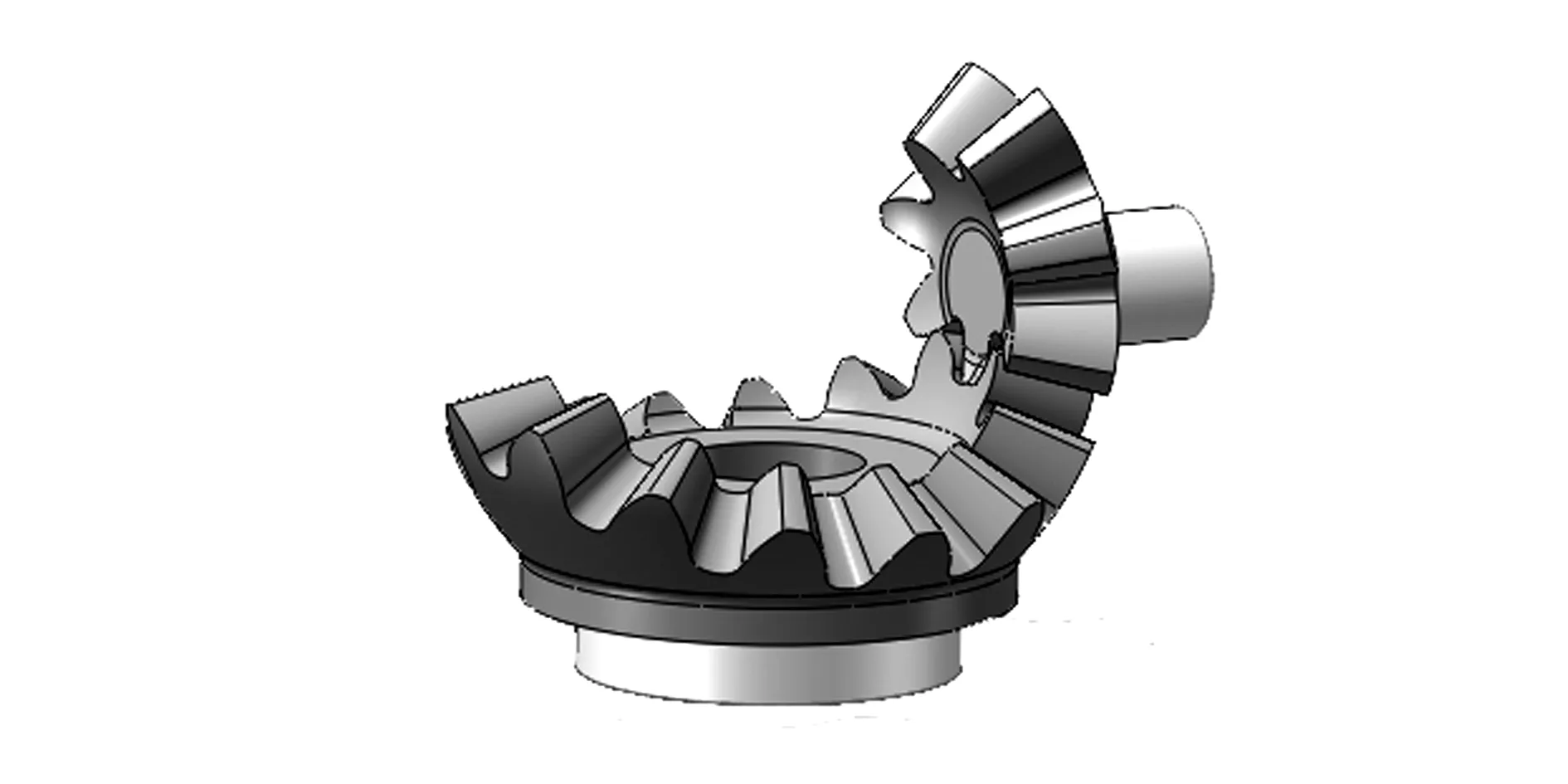
2 运动学仿真分析

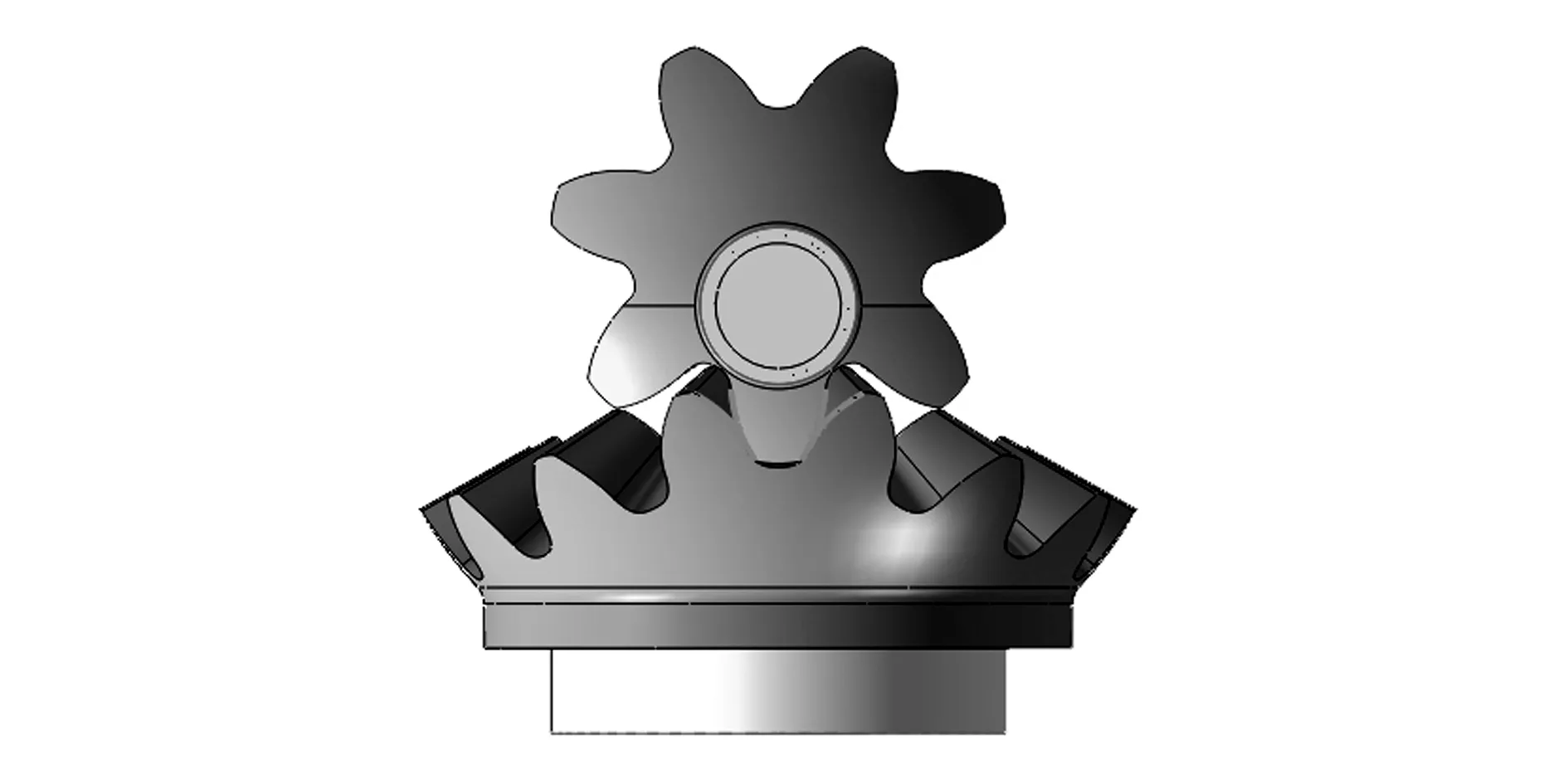
3 结 语

