基于子阵结构的相控阵M IMO雷达分辨能力分析*

文小乔，谭贤四，吕　伟，王力宝

（空军预警学院，武汉　430019）

基于子阵结构的相控阵M IMO雷达分辨能力分析*

文小乔，谭贤四，吕伟，王力宝

（空军预警学院，武汉430019）

在阵元总数一定的情况下，不同的子阵划分方式和布阵间距对不同子阵发射正交波形，子阵内发射相干波形的相控阵-MIMO雷达系统的分辨力的影响，首先通过相控阵-MIMO雷达的信号模型推导出其广义模糊函数，然后以此分析子阵结构对距离、多普勒、方位三维分辨力的影响。仿真结果表明，在阵元总数一定的情况下，子阵越多，系统距离分辨力越高，子阵越大，多普勒分辨力越高，子阵间距满足一定条件才能有较好的系统分辨力。这些结论对相控阵-MIMO雷达子阵结构设计具有指导意义。

相控阵MIMO雷达，广义模糊函数，分辨力，正交频分信号

0　引言

多输入多输出（Multiple InputMultiple Output，MIMO）雷达在发射端采用多天线同时发射相互独立的波形，然后在接收端多天线接收。根据阵元布置不同，MIMO雷达可分为两类：共置天线MIMO雷达［1］、分置天线MIMO雷达［2］。性能兼顾相控阵和MIMO雷达优点的相控阵-MIMO雷达也随之出现［3-6］，它在发射端将阵列划分为若干个子阵列，每个子阵列相干的发射相同波形的信号，这些子阵列之间发射互相正交的信号。它既能够有一定的相干增益，又可以实现波形或空间分集。

雷达系统分辨率由信号来决定，MIMO雷达的分辨率还与子阵的结构有关。上世纪90年代文献［7］对稀疏布阵综合脉冲孔径雷达的模糊函数及特性进行了分析。文献［2，8-12］研究了MIMO雷达的分辨特性。文献［13-14］推导了MIMO雷达的模糊函数，分析了其属性。文献［15］对MIMO-VSAR雷达的方位无模糊定位进行了研究，提出了优化方法。文献［16］对MIMO雷达距离旁瓣的抑制方法进行了研究。文献［17］对多载频MIMO雷达的模糊函数进行了分析，研究了系统的距离分辨力。文献［18］对接收分集MIMO雷达监测性能和模糊函数进行了研究。文献［19］对MIMO雷达和相控阵雷达的分辨力进行了比较。文献［20］研究了分布式MIMO雷达相干信号处理时的分辨能力。文献［21］对基于广义模糊函数的MIMO SAR分辨特性进行了研究。文献［22-23］分析推导了相控阵MIMO雷达的模糊函数及属性。文献［24］研究了正交高斯脉冲序列对MIMO雷达模糊函数的影响。总的来说关于MIMO雷达分辨力的研究主要从信号和阵列两个方面展开，对于相控阵MIMO雷达，前面的研究都没有对总阵元数一定的情况下，不同的子阵的大小、数目以及子阵的间距对雷达三维分辨力的影响进行分析，而子阵的结构对于相控阵MIMO雷达分辨力的影响是一个很有现实意义的问题。

基于上面的考虑，本文首先从相控阵MIMO雷达信号模型推导出其广义模糊函数，对阵元总数恒定，不同子阵结构的情况分别进行分析，并通过信号为正交频分LFM信号的仿真实验研究子阵的数目、大小、布阵间距对系统三维分辨性能的影响，最后分析结果，得到了对相控阵MIMO雷达子阵设计具有指导意义的结论。

1　相控阵-MIMO雷达信号模型

考虑一个多输入多输出（MIMO）雷达系统，它由M个发射天线和N个接收天线组成，如图1、图2所示。

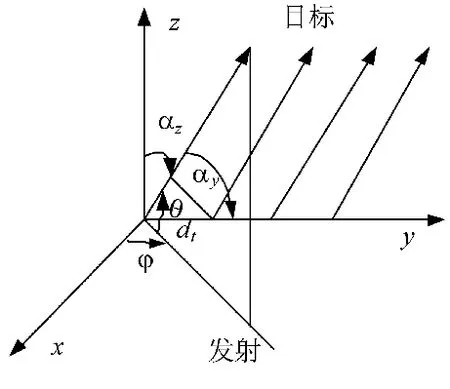
图1　MIMO雷达发射端结构

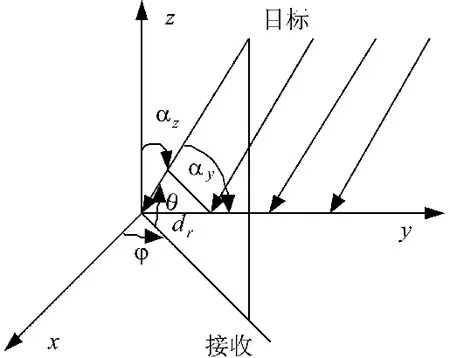
图2　MIMO雷达接收端结构

图中，dt、dr、φ和θ分别为发射阵元间距，接收阵元间距和目标方位和俯仰角，为了分析方便假设目标符合远场条件，收发阵列都为均匀线阵。M个天线的发射信号u（t）用式（1）表示。

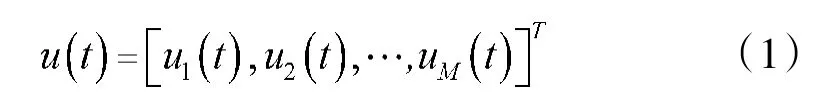
接收端的信号可表示为：

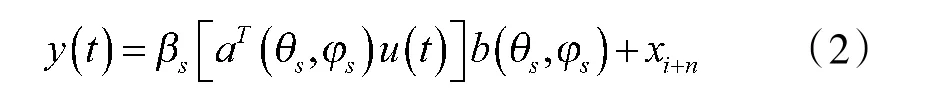
式中θs，φs为目标位置的俯仰角和方位角，βs为目标复反射系数，xi+n为机内噪声和外部干扰。a（θs，φs）和b（θs，φs）分别为发射和接收导向矢量，式中fc为发射信号频率和分别表示信号从第i个天线达到目标的时延，与第j个天线接收到信号的时延。

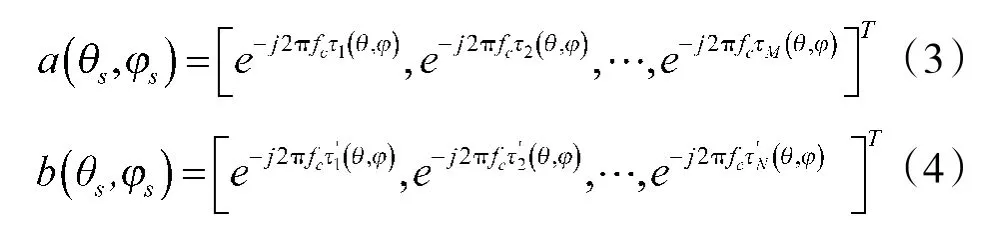
根据前面的假设，考虑M个阵元被划分为K个子阵，第k个子阵的发射信号复包络可以表示为［6］：

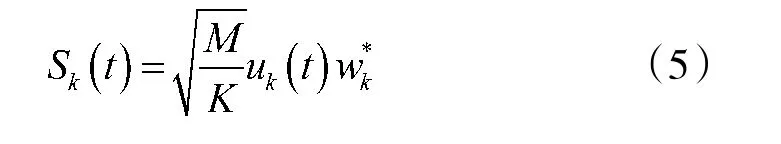
其中，wk为子阵的波束合成单位权向量，子阵间的发射信号能量是均等的，总能量为M，则在θs，φs方向发射的总信号为［19］：

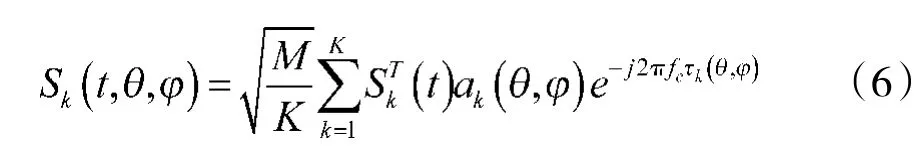
其中，a（kθs，φs）为第k个子阵的M/K个阵元的阵列内部导向矢量，fc如前所示为发射信号频率，（θ，φ）为第k个子阵的第一个阵元与参考阵元的信号传输相对时延，式（3）中的接收信号可以表示为：

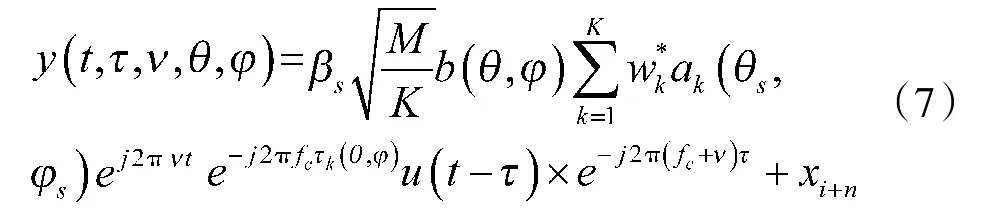
其中，υ为目标运动产生的多普勒频移，为了分析问题方便，忽略通道延时产生的频移，得到：

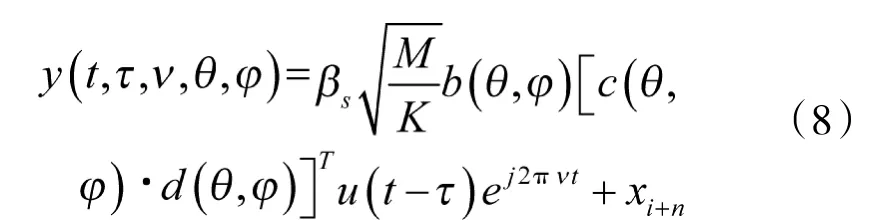
其中：

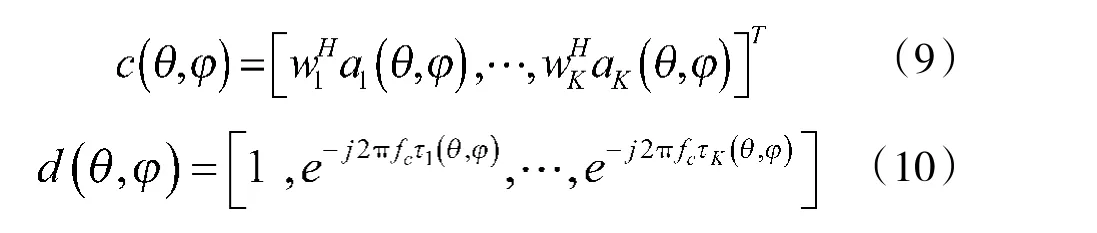
后面的分析都是在不考虑噪声和干扰的情况下进行，并且假设βs=1。

2　相控阵MIMO雷达广义模糊函数

模糊函数分析雷达的整体性能常用的切入点［25］，伍德沃德通过研究如何由已知的发射信号确定信号的时延参数和频移参数。雷达信号的模糊函数通常定义为：

u（t）为雷达所用信号，Δt为回波到达实际时间与匹配滤波器时差，Δf为回波为多普勒频移与匹配滤波器的频差。

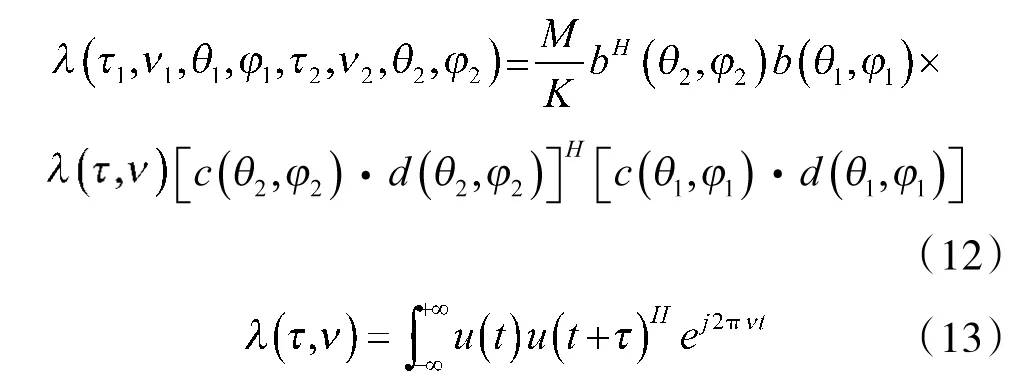
假设子阵的间距为ds，如图1、图2所示，相邻阵元的相位差因子为d cosαy也就是d cosθsinφ，进一步展开式（12）：

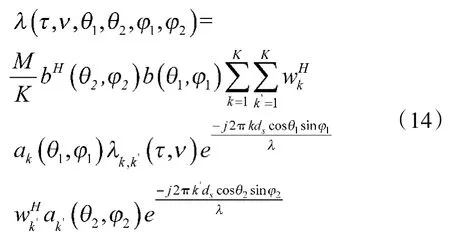
其中：

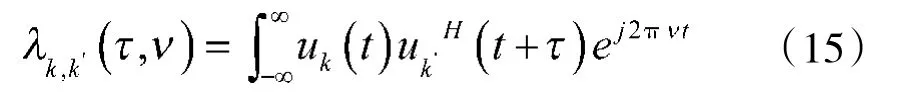
式（15）是影响分辨力的信号因素，b（θ，φ），c（θ，φ），d（θ，φ）为阵列因素，都会影响雷达系统的分辨力。

所有的子阵波束指向同一个方向，这样可以得到：

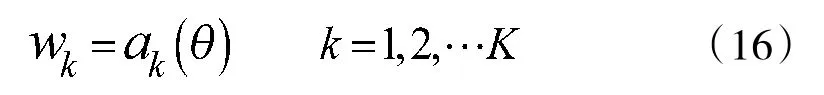
2.1均匀划分阵列

图3　发射阵列均匀划分

图4　发射阵列重叠划分

假设均匀线阵的子阵是均匀划分，如图3所示，每个子阵包含的阵子数为M/K个，子阵的间距ds为M/KdT，这样得到：

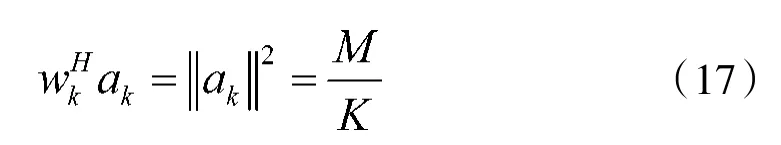
为了分析问题方便，系统假定天线收发共址得到：

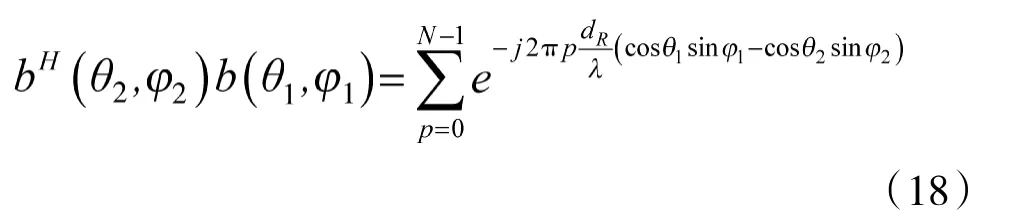
均匀划分子阵的相控阵MIMO雷达的广义模糊函数可以表示为：

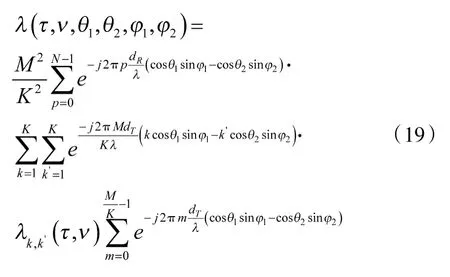
本文采用线性调频信号来进行分析，设K个子阵分别发射正交的的LFM信号［26］：

其互模糊函数：

将式（22）带入式（19）可得

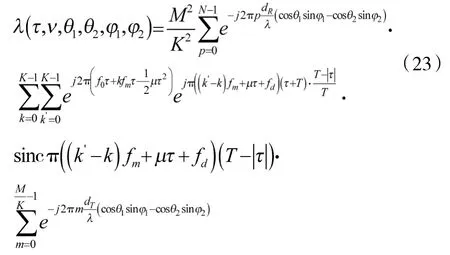
2.2重叠划分子阵列

假设均匀线阵的子阵是完全重叠的情况下，也就是每个子阵包含的阵子数为M-K+1个，子阵的间距ds为dT，这种子阵划分，相控阵MIMO雷达的广义模糊函数可以表示为：

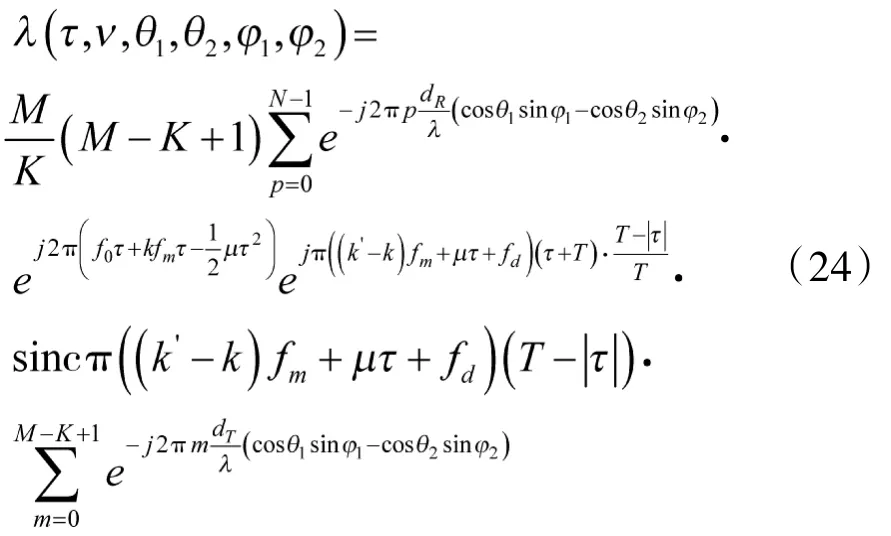
3　仿真分析

本实验取相控阵MIMO雷达的发射与接收阵列都是等间距布设的，阵元的间距为半波长，则阵列的方向信息为一维的（仅有方位角信息），LFM信号的中心载频fo为1GHz，子阵间发射信号频率之差fm为0.2MHz，信号带宽为3MHz。实验主要讨论子阵的个数，子阵内部的阵子数目，子阵之间的间隔对三维分辨力的影响。

实验1，总阵元数目一定的情况下，子阵个数变化对分辨力的影响。

首先取M=64，N=64，均匀划分子阵，子阵数目K=4和8时，分析其距离，多普勒和角度分辨力，这里角度分辨力为方位角（图1中的αz）。图5、图6是子阵数目为4和8时的距离多普勒模糊函数图。

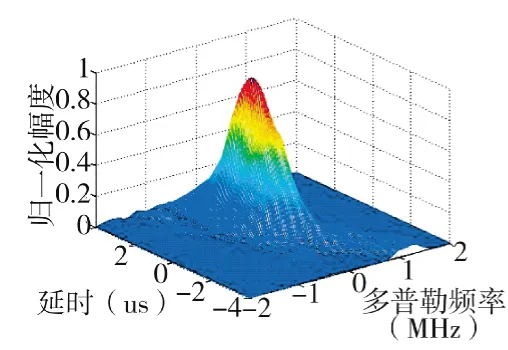
图5　均分4个子阵模糊函数图

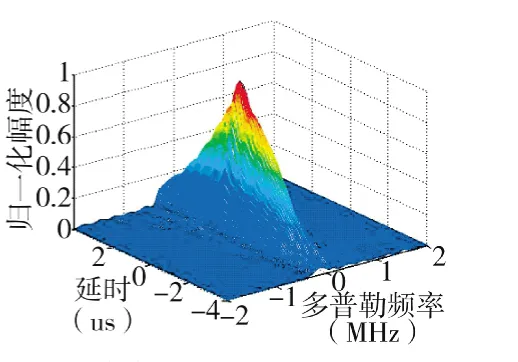
图6　均分8个子阵模糊函数图

取其等高线进行分析，如图7、图8所示。

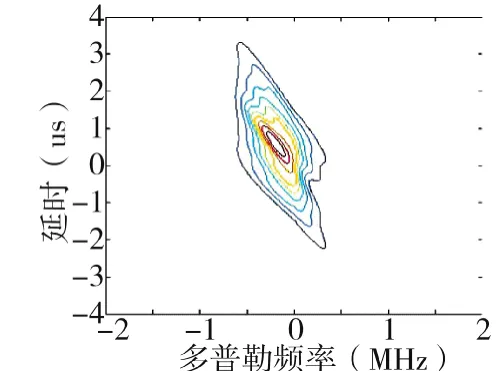
图7　均分4个子阵等高线图

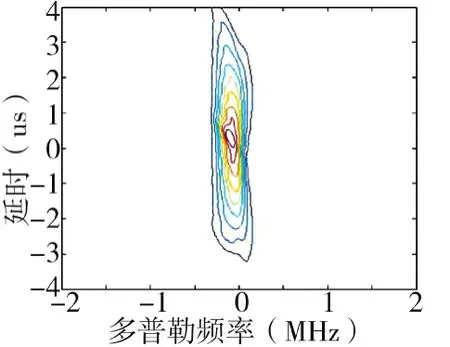
图8　均分8个子阵等高线图

再分析阵元总数保持不变，子阵数目变化时，角度-距离分辨力的变化情况如图9、图10所示。

结论1：如上所示，总的阵元数不变的情况下，子阵数目增加，每个子阵包含的阵元数相应减少的情况下，对距离分辨力有所改善，多普勒分辨力和角度没有明显变化。

这是因为，均分4个或者8个子阵，不会带来接收孔径的增大，这样角度分辨不会变化，本文在每个子阵间的频率间隔是一定的，而8个子阵会带来发射信号的总的带宽增加，进而改善距离分辨率。

实验2，总阵元数目和子阵数目均一定的情况下，子阵的大小变化对分辨力的影响。M=64，N=64，子阵数目K=4，这里使用前面提到的两种子阵划分方式，均匀划分与完全重叠划分，先考虑距离和多普勒分辨力的变化情况。

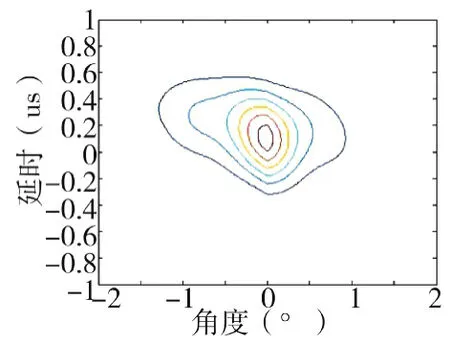
图9　均分4个子阵角度-时延等高线图

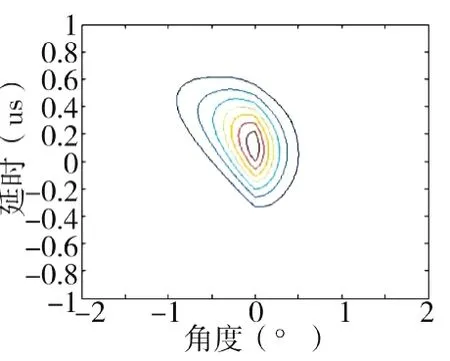
图10　均分个子阵角度-时延等高线图

图11　均分4个子阵模糊函数图

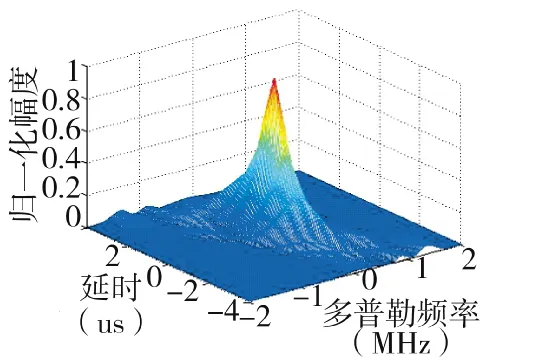
图12　重叠划分4个子阵模糊函数图

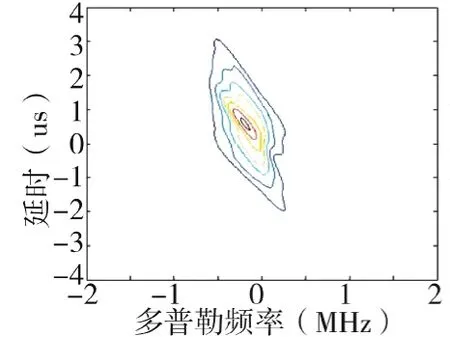
图13　均分4个子阵等高线图

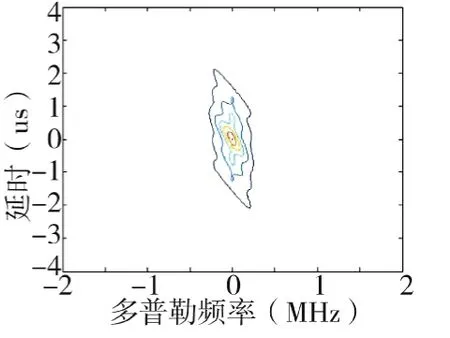
图14　重叠划分4个子阵等高线图

再取子阵数目K=8来讨论角度-距离分辨力变化的情况。

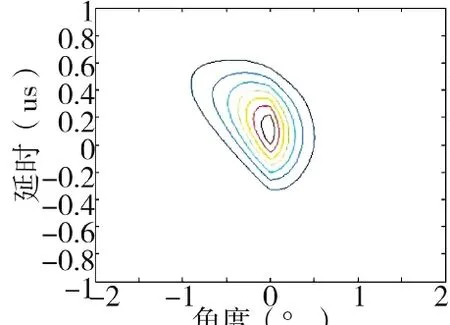
图15　均分8个子阵角度-时延等高线图

结论2：如上所示，总的阵元数不变，子阵数目恒定的情况下，采取均匀划分或者重叠划分的方式，每个子阵的阵元越多，多普勒分辨力有改善，距离、角度分辨力变化不大。

这是因为，均分或者重叠划分4个子阵，重叠划分时子阵包含的阵元数目较多，信号相参性相对好，进而多普勒分辨率较好，而距离分辨率由于信号总的带宽不变，角度分辨率由于接收孔径不变，均变化不大，8个子阵的情况与4个子阵的情况类似。

实验3，总阵元数目和子阵数目均一定的情况下，子阵的间距变化对分辨力的影响。

M=64，N=64，子阵数目K=4，均匀划分子阵，为了分析方便，发射子阵的间距取波长的整数倍，倍数分别为60、100、200、300。先考虑距离和多普勒分辨力的变化情况。

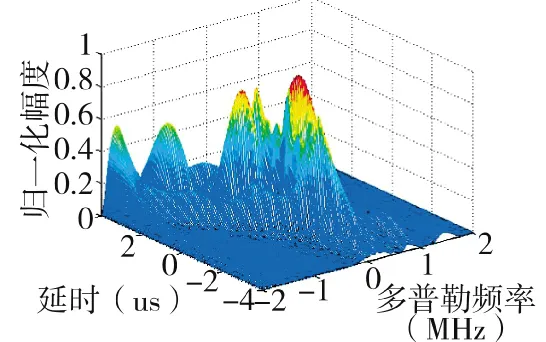
图17　间距60倍波长模糊函数图

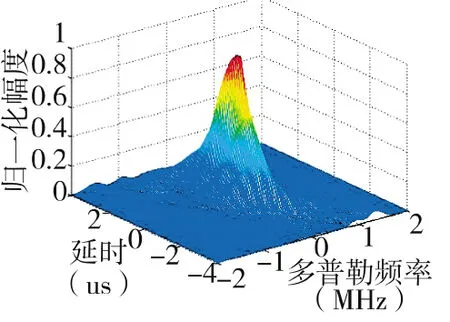
图18　间距100倍波长模糊函数图

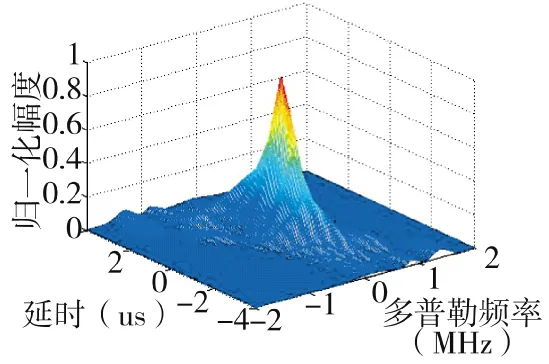
图19　间距200倍波长模糊函数图

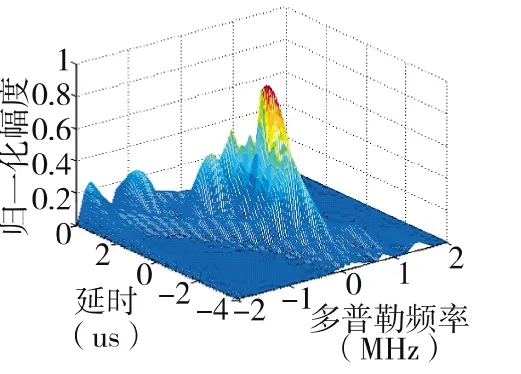
图20　间距300倍波长模糊函数图

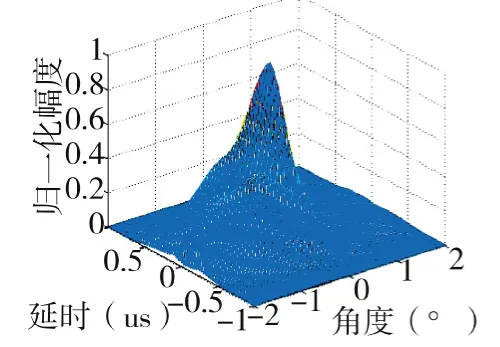
图21　间距60倍波长时延-角度模糊函数图

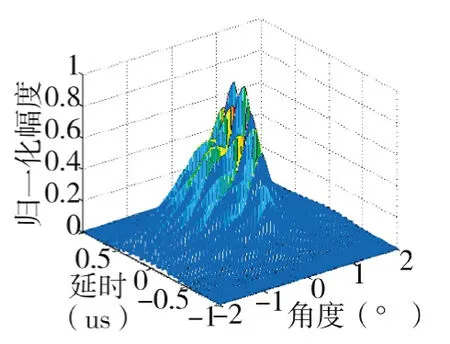
图22　间距100倍波长时延-角度模糊函数图

图23　间距200倍波长时延-角度模糊函数图

结论3：如上所示，总阵元数目和子阵数目均一定的情况下，均匀划分子阵的间距在100倍～200倍波长之间可以形成较为理想的距离-多普勒模糊函数。子阵的间距在60倍～200倍波长时，方位上的旁瓣会逐渐增强，方位分辨力会随着子阵间距变大而变差。

子阵间采用频率步进信号，可以有一定的栅瓣抑制效果。超出一定的范围难以维持这个效果。

4　结论

本文从相控阵MIMO雷达的信号模型，推导出了其广义模糊函数，将影响相控阵MIMO雷达分辨力的因素分为信号阵列因素，本文主要考虑子阵的结构和间距对分辨力的影响。分析和仿真实验表明：总阵元数一定的情况下①子阵数目增加，每个子阵包含的阵元数相应减少的情况下，对距离分辨力有所改善，多普勒分辨力和角度没有明显变化；②采取均匀划分或者重叠划分的方式，每个子阵的阵元越多，多普勒分辨力有改善，距离、角度分辨力变化不大；③均匀划分子阵的间距在100倍～200倍波长之间可以形成较为理想的图钉型距离-多普勒模糊函数。子阵的间距在60倍～200倍波长时，方位上的旁瓣会逐渐增强，方位分辨力会随着子阵间距变大而变差。本文的结论为相控阵MIMO雷达的子阵划分和布阵提供了理论依据。

［1］LI J，STOICA P.MIMO radar with colocated antennas［J］. IEEESignalProcessingMagazine，2007，24（5）：106-114.

［2］HAIMOVICH A M，BLUM R S，CIMINI L J.MIMO radar with widely separated antennas［J］.IEEE Signal Processing Magazine，2007，25（1）：116-129.

［3］BERGIN J，MCNEILS，FOMUNDAM L，etal.MIMO phased array for SMTI radar：IEEE Aerosp.Conf［C］//Montana：IEEE，2008：1-7.

［4］BROWNING JP，FUHRMANN DR，RANGASWAMY M.A hybrid MIMO phased-array concept for arbitrary spatial beampattern synthesis：IEEE Digital Signal Processing EducationWorkshop［C］//Marco Island：IEEE，2009：446-450.

［5］FUHRMANND，BROWNING P，RANGASWAMY M.Signal strategies for the hybrid MIMO phased-array radar［J］.IEEE J.Select.Topics SignalProcess，2010，4（1）：66-78.

［6］HASSANIEN A，VOROBYOV SA.Phased-MIMO radar：a tradeoff between phase-array and MIMO radars［J］.IEEE Trans.SignalProcess，2010，58（6）：3137-3151.

［7］陈伯孝，张守宏.稀布阵综合脉冲孔径雷达的四维模糊函数及其分辨率［J］.信号处理，1998，14（增刊）：33-37.

［8］FISHLER E，HAIMOVICH A，BLUM R，etal.MIMO radar：an idea whose time has come：IEEE Radar Conference［C］// Honolulu：IEEE，2004：71-78.

［9］MELVINW，HANCOCK R，RANGASWAMYM，etal.Adaptive distributed radar：Proceedings of the 2003 IEEE Radar Conference［C］//Bordeaux：IEEE，2003：71-78.

［10］BRUYERE D，GOODMAN N.Adaptive detection and diversity order inmultistatic radar［J］.IEEE Trans.Aerosp. Electron.Syst，2008，44（4）：1615-1623.

［11］KONGL，YANGM，ZHAOB.Adaptive detection for shared-spectrum multistatic radar in Gaussian clutte：IEEERadarConference［C］//Atlanta：IEEE，2012：0309-0313.

［12］SHTARKALEV B，MULGREW B.Multistatic single data set target detection in unknown coloured Gaussian interferenc：IEEERadarConference［C］//Ottawa：IEEE，2013：1-5.

［13］SAN ANTONIOG，FUHRMANND R，ROBEY FC.MIMO radarambiguity functions［J］.IEEESel.Topics Signal Process，2007，1（1）：167-177.

［14］CHEN C，VAIDYANATHAN P.Properties of the MIMO radar ambiguity function：IEEE ICASSP［C］//USA：IEEE，2008：1-5.

［15］戴喜增，许稼，彭应宁，等.MIMO-VSAR及其一种优化的阵列配置［J］.电子学报，2008，36（12）：2394-2399.

［16］戴喜增，许稼，彭应宁，等.FD-MIMO距离高分辨雷达及其旁瓣抑制［J］.电子与信息学报，2008，30（9）：2033-2037.

［17］杨明磊，陈伯孝，齐飞林，等.多载频MIMO雷达的模糊函数［J］.系统工程与电子技术，2009，31（1）：5-9.

［18］陈金立，顾红，苏卫民，等.基于接收分集的MIMO雷达性能分析［J］.火力与指挥控制，2010，35（5）：26-28.

［19］刘丛，黄建国，史文涛.MIMO阵列正交频分发射波形模糊函数分析［J］.计算机仿真，2010，27（10）：26-28.

［20］陈刚，顾红，苏卫民.分布式多入多出雷达相干处理二维分辨率分析［J］.电波科学学报，2012，27（2）：326-332.

［21］周伟，陈浩文，刘永祥，等.基于广义模糊函数的MIMO-SAR分辨特性分析［J］.国防科技大学学报，2013，35（6）：77-81.

［22］FUHRMANN D R，BROWNING JP，RANGASWAMY M. AmbiguityfunctionanalysisfortheHybridMIMO phased-array radar：IEEE Radar Conference［C］//Pasadena：IEEE，2009：1-6.

［23］WASEEM K，IJAZ M Q，KIRAN S.Ambiguity function of phased-MIMO radarwith colocated antennasand its properties［J］.IEEEGeoscience and Remote Sensing Letters，2014，11（7）：1220-1224.

［24］BOGOMIL S，BERNARD M.Effects of FDMA/TDMA orthogonality on the gaussian pulse train MIMO ambiguity function［J］.IEEESignalProcessing Letters，2015，22（2）：153-157.

［25］马晓岩，王党卫，杨军.现代雷达信号处理［M］.北京：国防工业出版社，2012：55-57.

［26］陈正中，李小波，梁浩，等.正交频分LFM信号的MIMO雷达的匹配滤波技术［J］.雷达科学与技术，2013，11 （2）：197-202.

Resolution Analysisof Phased-M IMO Radar Based on Subarray Configuration

WENXiao-qiao，TANXian-siWei，WANG Li-bao
（Air Force Early Warning Academy，Wuhan 430019，China）

It is very important for phased-multiple inputmultiple output（MIMO）radar systems to make sure how to partition the transmit array in order to satisfy the requirements of performance. Firstly，the generalized ambiguity function of the MIMO radar into Phased-MIMO radar is extended. Then，the influence of the subarray configuration on range，azimuth，and doppler resolutions are analysed，If the sum of transmitter is assured，the simulation results indicate that the more subarrays are，the better range resolutions is，the bigger subarrays are，the better doppler resolutions is.These conclusion are crucially guiding for subarray configuration.

phased-MIMO radar，generalized ambiguity function，resolution，orthogonal frequency division signal

TN957

A

1002-0640（2016）08-0041-06

2015-06-11

2015-08-07

国家自然科学基金资助项目（61201451）

文小乔（1982-），男，湖北公安人，讲师，硕士。研究方向：M IMO雷达信号处理、认知雷达技术。