取水监测优化布局技术研究

郝 震，蒋云钟，赵红莉，王海宁

（1. 兰州交通大学测绘与地理信息学院，甘肃 兰州 730000；2. 中国水利水电科学研究院，北京 100089）

取水监测优化布局技术研究

郝 震1，2，蒋云钟2，赵红莉2，王海宁2

（1. 兰州交通大学测绘与地理信息学院，甘肃 兰州 730000；2. 中国水利水电科学研究院，北京 100089）

我国自 2012 年开始实施国家水资源监控能力建设项目，依据取水许可证登记的取水许可量，对规模以上的 10 000 多户取用水进行在线监测，但对于规模以下的取用水户由于量多面广投资巨大而缺乏监测。针对规模以下的取用水监测布局进行优化技术研究，在遵循科学经济的前提下，构建基于抽样效应的复杂抽样样本量计算模型，进行样本分配方式的优化选择和误差估计，并以典型省份的工业用水为例进行取水监测优化布局技术应用验证。结果表明：采用分层抽样技术不仅可以有效减少取水监测点的布局数量，降低取水监测成本，还有利于得到更优化的取水总量推算结果，研究对于全国各省份开展取水监测优化布设工作具有重要参考价值。

取水监测；优化布局；抽样技术；取水总量预估

0　引言

取水监测是掌握区域取用水状况的重要基础，也是实行水资源开发利用控制红线管理的重要信息来源。2012 年始，水利部和财政部共同组织实施国家水资源监控能力建设项目，重点对河道外地表取水年许可取水量在 300 万m3以上和地下取水年许可取水量在 100 万m3以上的 10 000 多户规模以上的颁证取用水户进行在线监测［1］，基本可以监测全国年许可河道外取水总量的 70%，约占全国总用水量的1/3。但对于规模以下的数十万取用水户，由于量多面广投资巨大而缺乏监测。取水监测范围不完善，将会影响取水监测的效果，进而影响对全国取水总量信息的全面掌握程度。

通过分析全国取水许可台账数据可知，河道外年许可取水量 100 万m3以上与 100 万m3以下的取水用户基本呈现“一九”规律分布，即前者数量仅占全国总取水户数的 10%，但其许可取水量之和占全国总许可取水量的 90% 左右，而后者刚好相反。因此，国家水资源监控能力建设项目重点针对规模以上取用水进行监测是行之有效的，但对于未纳入项目监控范围的大量规模以下取用水也需要掌握取用水特点，以更全面掌握全国取水总量信息［2-4］。由于规模以下的用水户具有数量庞大的特点，要全面掌握这一取水区间的实际用水情况，需进行取水户取水量的监测，若全部进行监测，实现难度高且投资效益低。为此对规模以下的用水户进行抽样监测，研究重点是在科学经济的原则下对规模以下取水监测进行优化布局研究。

关于抽样方法及应用研究，部分学者已经开展了探索。金勇进在抽样技术中对分层抽样方法及方法选择进行了描述［5］；刘建平对分层抽样的分层层界划分进行了研究［6］；袁建文对分层随机、整群、二阶段等抽样样本量确定公式进行了推导，并给出了样本量经验判断参考［7］；张勇用实例对抽样样本量的多少进行了验证，得出样本并非越多越好的结论［8］。这些研究只是对抽样方法进行了研究，并没有应用在用水户与取水量的调查中。何小菊对工业行业供用水统计抽样方案进行了探讨，采用简单随机抽样方法确定抽样样本量，再根据以往统计调查方法确定样本分配数量，并对比了简单随机与分层 2 种抽样在工业行业中抽样结果的优劣，提出分区制定对全国工业行业样本量的指导意见。在现有的取水监测布局研究中，何小菊已经对全国各省工业行业取水监测布局技术进行了探讨，并对各省工业行业取水许可总量进行了聚类分析，将全国省份按取水许可总量分为 3 类，对每一类省份给出了合适的抽样样本经验值［9］。但此方法并没有准确地分析各省工业行业取水用户的取水特点，导致各省在实际监测选点过程中出现样本选取重点不明确的问题。因此需要具体分析用水户在各个许可取水量区间的分布特点，对样本选取重点进行分析，从而得到更加具体，目的更明确的取水监测布局优化方向。

为此在相关研究基础上，提出采用统计学的相关理论方法开展取水监测优化布局研究。具体来说，以全国取水许可台账数据为抓手，采用复杂抽样技术对规模以下的取水户进行抽样监测研究，即在遵循科学合理、经济可行的前提之下，研究取水监测抽样设计的思路和方法，并选取典型地区和行业进行实验验证，以期为推进实施国家水资源监控能力建设项目提供理论参考依据。

1　取水监测优化布局技术研究

取水监测优化布局的思路是，从整体用水量角度出发，以全国取水许可台账作为数据源，首先采用分层抽样方法调查全国取水户，较为真实地反映规模以下的取水户情况和各区间的取水许可量；其次考虑取水监测的抽样成本和精度，合理划分抽样区间，确定层数、各区间内的方差和离散程度，用于辅助进行抽样监测；再次构建基于抽样效应的复杂抽样方案样本量计算模型，进行样本分配方式选取和误差估计。该研究方法能够满足省级尺度下的样本选点与实际用水量预估，各省可以依据取水监测优化布局研究方法结合本省取水许可台账数据，按照一定步骤完成对取水户的样本量确定及各省实际用水量预估工作。

1.1分层抽样区间的划分

本研究采用累积平方根法作为分层抽样区间划分的方法，核心思想是将分层变量（例如 Xi）分布的累积平方根进行等分获得最优分层。该方法是由戴伦纽斯（Dalenius）与霍捷斯（Hodges）提出的，优点是合理地对调查目标进行分层，可以提高抽样效率。对全国取水许可台账数据进行筛选，提取出取水量 100 万m3以下的取水户作为抽样总体进行数据分析，对许可水量划分区间，分别统计各区间内取水户数量，对各区间内用水户数量 ƒ 进行开方处理，累加各区间用水户数量开方结果。

1.2分层抽样层数的确定

若分层抽样按自然层或单元类型划分，则层数是自然的；如运用累积平方根法进行分层，则会存在确定层数的问题。分析分层与简单随机 2 种抽样方式，分层抽样的精度要高于简单随机抽样。是否层数划分的越多，分层抽样得到的结果越好，需要分析涉及层数增加时估计量方差的下降速度。

首先考虑以目标量本身作为分层指标。以最简单的情形为例，Yi（研究整体的样本值）是区间 d 上的均匀分布，则总体方差，样本量为 n 的简单随机抽样估计量的方差为

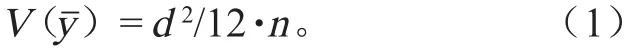
将总体分成大小相同的 L 层，并按比例分配样本量，即 Wh= 1/L，nh= n/L，则总体均值误差的无偏估计为

式中：Wh与 nh分别为第 h 层的层权与样本量个数；为 h 层的方差；为样本量为 n 的样本均值。由此可见，层数的增加确实能提高估计精度。

分层工作中，Yi本身未知，只能通过与 Yi高度相关的辅助指标 Xi进行计算。这时估计量的方差可以分为 2 部分，一部分与层数有关，另一部分与层数无关，用模型表示即 R2/L2+（1- R2），其中 R2是方差中受层数影响的部分，（1-R2）是不受层数影响的部分。因此，当层数增加到一定的时候，在精度上的收益将非常小。根据研究，除非 Y 与 X 的相关系数 p ＞ 0.95，层数一般以不超过 6 层为宜。

对比层数分别为 4，5，6 时划分的分层界限结果，当层数为 4 时，区间边界的划分与累积平方根对应结果出入较大，影响区间边界的确定，增加分层误差；层数为 6 时，分层区间边界划分过细，不仅增加了样本计算难度，增加了抽样成本，还对抽样结果的精度无较大影响。因此选定分层层数为 5，利用累积平方根结果与层数划分层界，取层数 5 与累积平方根结果 1 843.37，则应每间隔 1 843.37/5 = 368.67 分 1 层。由此得到的较为合理的分层为 100≥x＞35，35≥x＞15，15≥x＞5，5≥x＞1，1≥x＞0。

1.3复杂抽样方案样本量的计算方法

复杂方案的样本容量计算公式为 n = n*×deff，n* 为简单随机抽样的样本容量，deff 为设计效应，即相同样本量下复杂方案与简单随机样本下估计量方差的比率［5］。给定误差限和置信度的简单随机抽样样本量，则简单随机抽样的总体均值误差公式为

式中：uα/2为双侧百分位点，依据置信度求得。

依据累积平方根的方法将用水户分为 h 层，按Neyman 法则进行分配的分层抽样中，总体均值误差的一个无偏估计为如下形式：

式中：Wh为第 h 层的层权。

相同样本量下的简单随机抽样对总体均值估计量方差的一个无偏估计为如下形式：

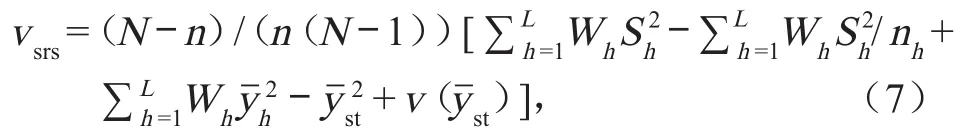
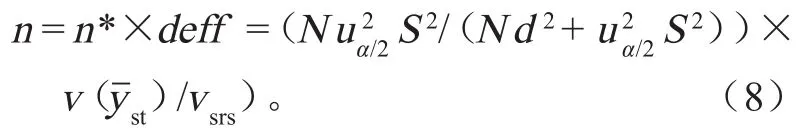
运用样本量确定方法处理全国取用水许可台账数据，可估算全国所需抽样的监测点个数，通过研究估算全国抽样监测点数量可以为各省选取监测样本点提供参考。在省级尺度上，各省可以依据该研究方法，结合本省各取水行业的取水特点，计算本省的抽样监测点个数。在不分取水行业的条件下，分别统计全国已划分取水量区间的用水户数量 n，层权 W，区间方差 S，均值 y，结果如表 1 所示。

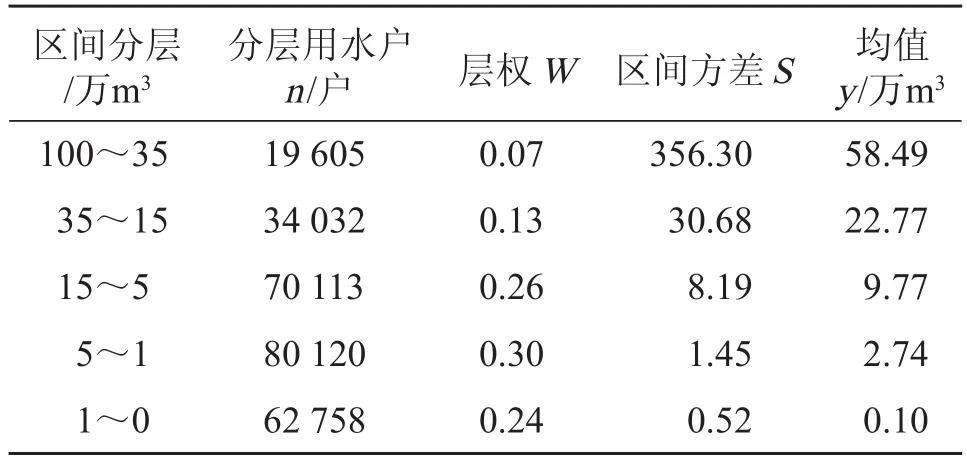
表1　分层区间信息统计表

取水台账数据百万以下用水户的取水量总方差为 262.93，要求在 95% 置信度下，相对误差 10% 以内的条件下，计算分层抽样总样本量，计算结果如表 2 所示。表 2 中的 n 即为与简单随机抽样相同精度和置信度条件下分层随机抽样的样本量。

表2　复杂抽样样本量计算结果统计表

1.4样本的分配方式与预估误差

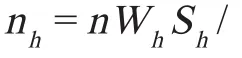
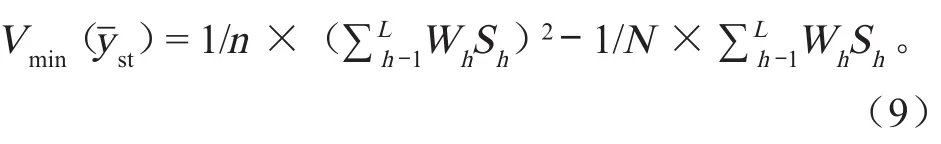
依据分层抽样样本预估总量 y 为

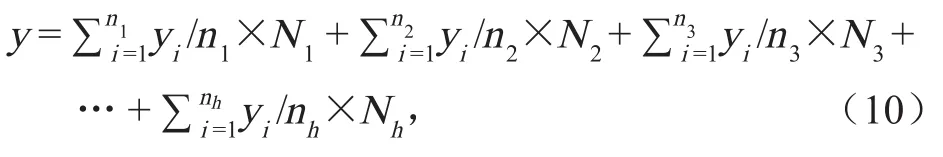
式中：Nx代表 x 层的用户总量；nx代表 x 层样本数量。

预估误差 p = y/Y×100%。

根据总样本量，按研究方法中的 2 种分配方法，同时将样本量进行分配，分配结果如表 3 所示。

表3 结果表明，2 种分配方式下，各层所分样本量差距较大，为验证 2 种不同分配方式在用水总量方面的预估精度，对 2 种方式分别进行了 10 次随机数检验，对比 2 种方式在用水总量预估问题中的适用性。同时在相同样本量情况下，得到简单随机抽样预估结果。汇总 3 个实验的预估总量与统计总量百分比结果，绘制成如图 1 所示的预估精度汇总图。从图 1 可以得出在相同样本量的条件下，随机实验 10 次，分层抽样的 2 种分配方式预估精度普遍要高于简单随机抽样结果。分层抽样 2 种分配方式的预估结果精度都在 98% 以上，这样的总量预估结果能满足实际项目的需求。需要说明的是由于采用的是随机数模拟预估结果，随机数是在取水许可证中的取水许可量上抽取得到的，与实际取水量无关。但 Neyman 分配的结果精度方差要小于按比例分配的结果，所以在本研究条件下选取 Neyman 分配方式更优。

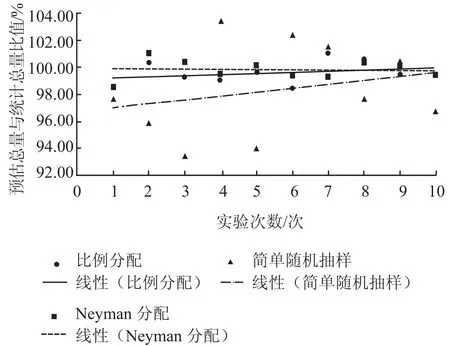
图1　预估精度汇总图

2　取水监测优化布局技术应用实例

2.1实验省份选取

我国各省份因地理位置不同，取用水结构也不尽相同，对我国各省份的工业行业用水情况进行聚类分析，在 SPSS（统计产品与服务解决方案）软件中输入取水台账数据中的全国各省份工业行业的用水户与取水量数据，对各省份工业用水情况进行聚类，结果如表 4 所示。

表4 中，第 1 类为高工业用水省份，第 2 类为较高工业用水省份，第 3 类为中等工业用水省份，第 4 类为低工业用水省份，前 2 类省份中主要为东部和南部省份。本研究提到的样本量确定方法适用于第 1 和 2 类省份，而第 3 和 4 类省份，工业用水户少，取水量低，运用分层抽样进行优化抽样结果不明显，为此实例分析选取第 1 和 2 类省份。

表4　聚类分析结果统计表

2.2实验验证

选取东部省 A 与南部省 B 工业用水作为实例进行抽样模拟。首先分别对 A 与 B 省按照样本量确定方法与分配方案进行样本量计算，得到样本量与分层分配方案；然后运用累积抽样的方法对每个抽样方案分别进行 250，500，…，3 000 次抽样模拟；最后对每个抽样方案的精度进行分析与对比。在给定相同绝对误差限与置信度的条件下，计算得出 A 省样本总量为 2 045 个，B 省样本总量为 1 722 个。根据分层抽样样本分配方式分配的样本量如表 5 和 6所示。

表5　A 省样本量确定与层间样本分配表

表6　B 省样本量确定与层间样本分配表

得到 2 省的样本层间分配量，即可预估台账数据中的许可总量，统计许可总量并与 2 省的预估总量进行对比，结果如图 2 和 3 所示。

分析 2 个精度对比图，可以得出在分省分行业尺度条件下，研究的样本量确定方法能够较快地计算出适宜的样本量个数。A 省样本量计算结果为2 045 个，结合图 2 中的简单随机与分层抽样 2 种分配方式折线分析，在样本量为 2 000 次时，分层Neyman 分配抽样精度已经明显高于简单随机抽样折线，Neyman 分配的抽样精度也要优于比例分配；B省样本量计算结果为 1 722 个，图 3 表明，3 条折线在样本量为 1 750 个时趋于稳定，虽然简单随机抽样折线的精度接近于比例分配折线，但简单随机抽样存在影响离散度的不稳定因素。由实例分析可以得出 Neyman 分配在相同样本量的情况下，精度要高于简单随机与分层比例分配样本量 2 种抽样方式，并且抽样精度稳定性较强的结论。

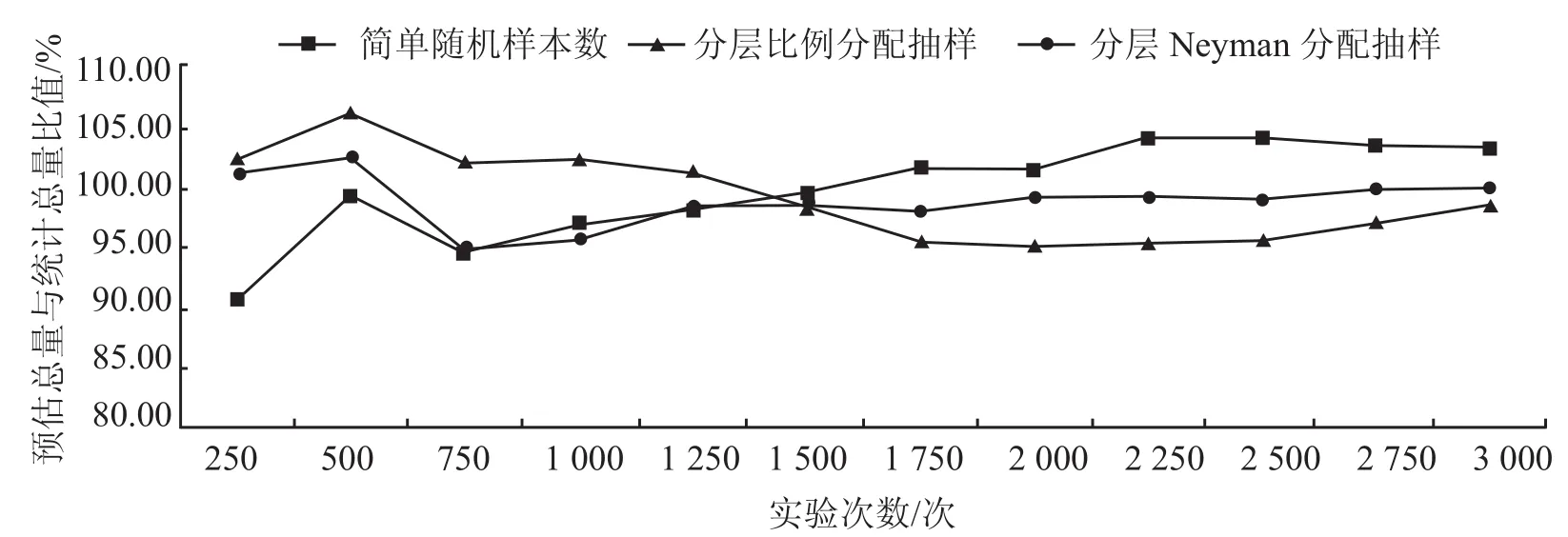
图2　A 省抽样精度对比图

图3　B 省抽样精度对比图

3　结语

通过对我国许可取水分布特点的分析，对规模以下取水监测布局方式进行了优化研究，提出了抽样监测方式，对通过样本监测数据推算取水总量进行了说明，并从实例的层面上对研究方法进行了验证。研究结果表明，该抽样方法能够起到优化样本量选择与总量推算结果的作用。本研究所选用的抽样方法不仅能够合理计算抽样样本量，而且能在实际分析中起到优化样本分配，减少抽样成本并提高预估精度的效果。该方法还可以运用到取用水监测的公共供水与其他用水行业的取水量预估中。但在农业取水量预估方向中，选取样本并不能充分考虑灌区种植结构与用水量之间的关系，所以此方法并不完全适用于农业样本量选取与取水总量预估，仍需统筹考虑该抽样方法与农业灌区取水特点预估农业取水总量。

［1］ 中华人民共和国水利部，财政部. 国家水资源监控能力建设项目实施方案（2012—2014 年）（水资源［2012］ 411 号）［A］. 北京：中华人民共和国水利部，2012: 1-23.

［2］ 蒋云钟，万毅. 水资源监控能力建设功能需求及实施策略［J］. 中国水利，2012 （7）: 26-30.

［3］ 金喜来，甘治国，陆旭. 国家水资源监控能力建设项目建设与管理［J］. 中国水利，2015 （11）: 24-25.

［4］ 蔡阳. 国家水资源监控能力建设项目及其进展［J］. 水利信息化，2013 （6）: 5-10.

［5］ 金勇进，蒋妍，李序颖. 抽样技术［M］. 北京：中国人民大学出版社，2002: 40-63.

［6］ 刘建平，方越峦. 分层抽样层界限确定方法研究［J］. 统计与决策，2012 （3）: 9-11.

［7］ 袁建文，李科研. 关于样本量计算方法的比较研究［J］. 统计与决策，2013 （1）: 22-25.

［8］ 张勇. 样本量并非“多多益善”——谈抽样调查中科学确定样本量［J］. 中国统计，2008 （5）: 45-47.

［9］ 何小菊. 工业行业供用水统计抽样方案的研究与探讨［D］.北京：中国人民大学，2013: 36-43.

Research on Technology of Water Monitoring Layout Optimization

HAO Zhen1，2，JIANG Yunzhong2， ZHAO Hongli2， WANG Haining2
（1.College of Geomatics of Lanzhou Jiaotong University， Lanzhou 730000， China；2. China Institute of Water Resources and Hydropower Research， Beijing 100089， China）

The national water resources monitoring capacity building project has been implemented since 2012 in our country. On the basis of the water intake permit scales which is registered， it has already monitored more than 10000 water users above the scales. There are more water intake users without water intake monitoring due to huge quantities and investment. Based on the no monitoring water layout optimization technology research， on the premise of following the science and economy， the article builds the complex sampling sample size calculation model based on the sampling effect， carries out allocation optimization and error estimate of mode of samples distribution selection，and using industrial water in typical provinces as an example for layout optimization technology applied for water monitoring. The results show that the stratified sampling technology can not only effectively reduce the number of layout of water monitoring， reduce costs of water monitoring， and get better prediction results also. The research has important reference value for the national each province to carry out the water monitoring optimization deployment.

water monitoring； optimized layout； sampling techniques； water consumption forecast

TU991.1

A

1674-9405（2016）04-0026-06

10.19364/j.1674-9405.2016.04.006

2016-04-13

郝 震（1991-），男，陕西西安人，硕士研究生，主要从事水文遥感方面的研究。