线阵干涉仪解模糊算法研究

田　冰

(西安电子科技大学 电子工程学院，陕西 西安 710071)



线阵干涉仪解模糊算法研究

田冰

(西安电子科技大学 电子工程学院，陕西 西安 710071)

针对线阵干涉仪在测向过程中由于相位周期性模糊导致的测向模糊问题，比较了长短基线法和统计相位方差法的不同特点。在不同信噪比条件下及不同短基线间距条件下，对两方法进行理论分析与仿真对比。结果表明，在低信噪比条件下统计相位方差法相对于长短基线法有较高的解模糊准确度和稳定度，对信号的适应能力强。而短间距的改变对统计相位方差法的测量误差影响大。

干涉仪；测向；解模糊；统计相位方差法

随着电子战[1]技术的不断发展，军事科技不断进步，无源定位技术得到了飞速发展[2-4]，其中一种应用较广泛的方法[2]是线阵干涉仪测向法，其具有测向精度高、灵敏度高、运行效率高和算法简单等优点[3]。线阵干涉仪测量过程中由于测量相位的周期性,会在计算相位角过程中产生整数倍周期模糊，这对测方位角有较大影响，故解模糊是干涉仪测向技术中的关键[4]。常用的解模糊算法很多，解模糊结果的准确度不仅和算法有关，也和环境器件等因素有关。本文重点仿真并讨论了常用的解模糊算法，即长短基线法[5]和统计相位方差法[6]。并且在不同信噪比[7]和不同基线间距情况下对两方法进行了对比。

1　长短基线法

长短基线法解模糊的核心思想就是通过短基线逐级求解上一级长基线的无模糊相位差。短基线可保证相位差无模糊，长基线能提高测量精度，以三路基线分析原理如图1所示。

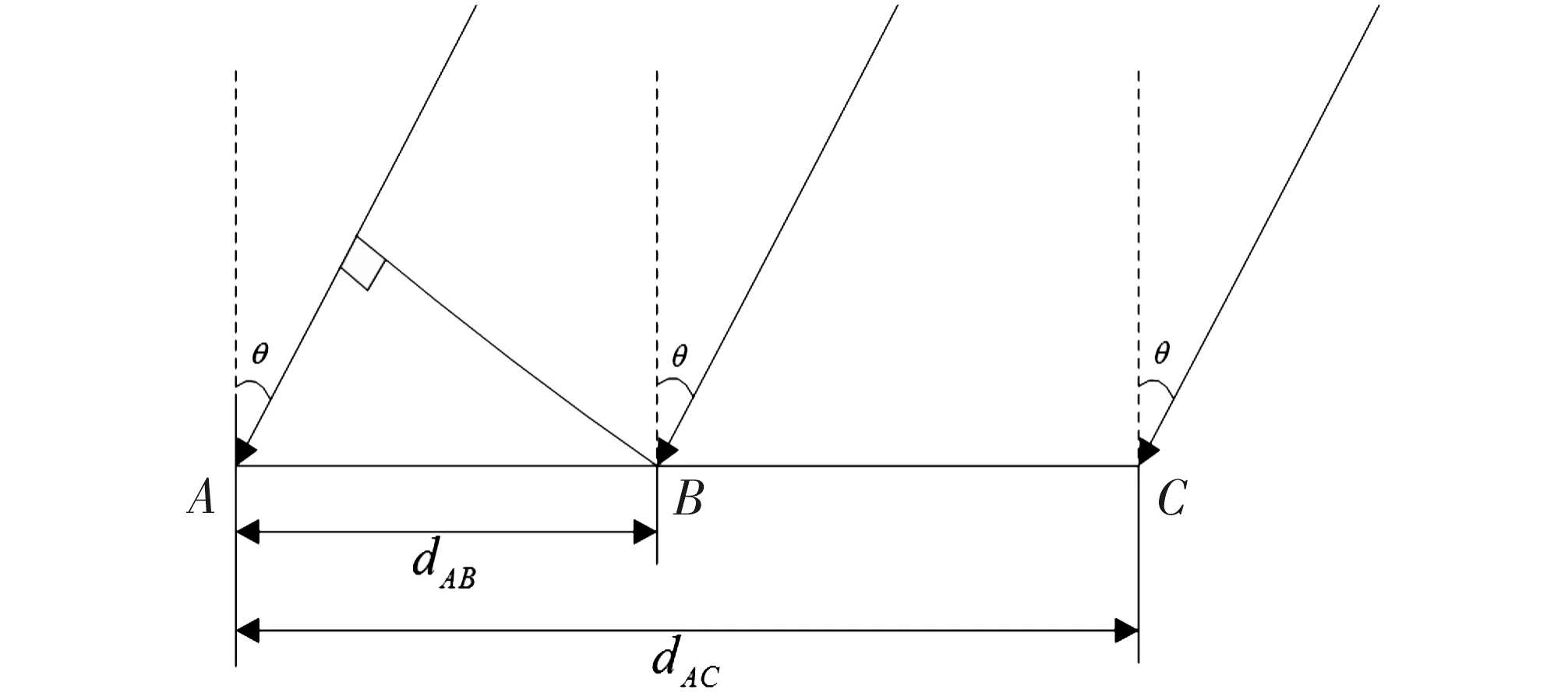
图1　解模糊原理图

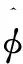
(1)

2　统计相位方差法

该方法首先求得最长基线的所有信号点所对应的角度，然后求出每条基线所对应的相位差，接着将求出的相位差和原来基线测量的原始相位差进行对比，可得到误差方差的最小点，这一点所对的相位差即为该基线无模糊相位差，其所对的相位即为真实相位。

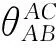
(2)

(3)

(4)

找出ξ(i)(i=1,2,…,N)中的最小值，即为最小均方误差，其对应的角度即为最长基线的真实无模糊相位差值。

3　解模糊方法仿真比较

长短基线法在进行相位计算时，是用短基线逐级计算长基线方位角，解模糊的过程中不能充分利用所有的基线相位差测量信息，且有可能将测得的相位误差逐级放大。统计相位方差法是通过最长基线计算其他基线相位差，可充分利用所有基线相位差的测量信息。

在Matlab环境下，采用同样的仿真条件对这两种解模糊方法进行仿真对比。统一输入条件为：(1)仿真信号为常规单载频信号；(2)频率400 MHz，采样率1 GHz，采样点数1 024；(3)入射角度为30°；(4)变信噪比条件下短基线间距为0.06 m，相邻基线比为6，信噪比测量范围从-10～30 dB，以0.4 dB为步进仿真值，每个信噪比仿真100次；(5)变短基线间距条件下信噪比为20 dB，相邻基线比为6，短基线间距测量范围0.01～0.5 m(此时半波长是0.375 m)，每个间距仿真100次。

3.1信噪比变化仿真对比

在不同的信噪比条件下，相位差的测量对比结果如图2所示。

图2　信噪比变化对解模糊影响

图2展示了当信噪比从-10～30 dB变化时，长短基线和统计相位方差解模糊算法的对比仿真情况。当从-10 dB增加到5 dB时，信噪比对两种解模糊方法的影响较大。当信噪比变小时，两种解模糊方法误差变大。在信噪比为-10 dB时，相位差真值为86.4°，统计相位方差解模糊得相位差为200°，而长短基线法的相位差约为1 000°。通过对图2分析可得到，在信噪比很低时，统计相位方差解模糊方法的误差比长短基线法小。

长短基线法由于是用短基线逐级计算长基线方位角，解模糊的过程中将测得的相位误差逐级放大。在信噪比较低时，短基线测得的相位角误差较大，由于误差的逐级累加而导致长基线误差过大。统计相位方差法是通过最长基线的测量角计算其他基线相位差，最长基线测得的相位差最准确，可避免误差的逐级累加，且统计相位方差法充分利用所有基线测量值参与解模糊，由此可避免噪声强度高而引起的测向误差。

3.2短基线间距变化仿真对比

在短基线间距变化的条件下，相位差测量对比结果如图3所示。

通过分析图3可知，当短基线间距在0.01 m左右时，两种解模糊方法误差均较大，但统计相位方差法比长短基线法的误差小很多。当短基线在0.01～0.03 m时，长短基线法误差依然较大，相位方差估计值和真值很近。当短基线长度为0.03～0.24 m时，两者的误差均较小，估计值与真值接近。当短基线长度>0.24 m时，长短基线法的误差不变，而统计相位方差法的误差增大。

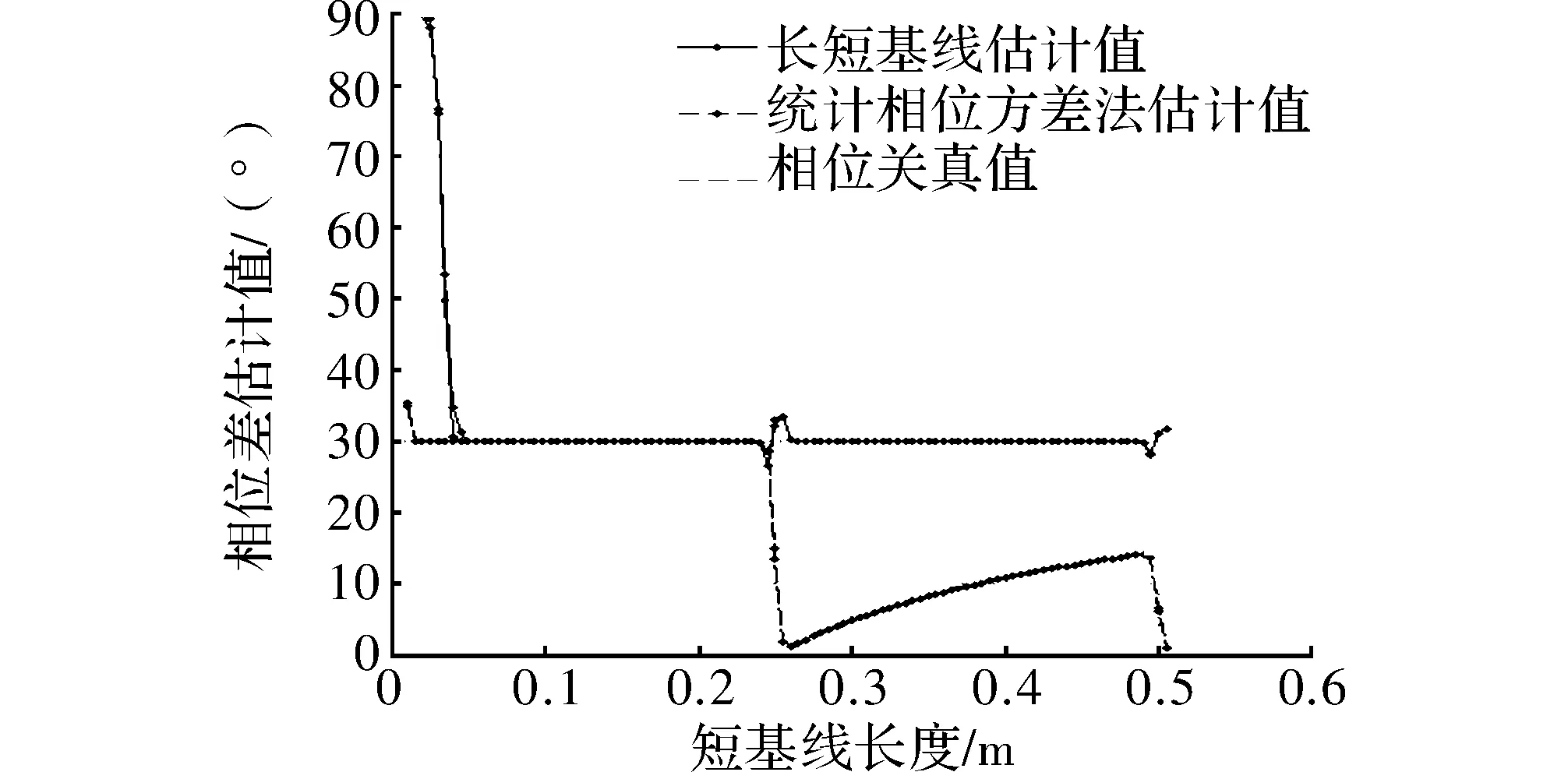
图3　基线间距变化对解模糊影响

长短基线法由于是逐级求解相位差，短基线间距变大带来的影响较低；统计相位方差法在解模糊的过程中充分利用了所有基线测量值，短基线间距变化带来的影响会反应到所有基线的测量值上，这样会将影响累加，最后影响统计相位方差法的测向精度。

4　结束语

长短基线法的计算方便简洁、步骤少、求解相位的速度快，但其缺点是解模糊时未充分利用所有的基线相位差测量信息，有可能将测得的相位误差逐级放大。短基线间距变化对长短基线法解模糊的效果影响较低，但对低信噪比的适应能力差。统计相位方差法对信噪比变换的适应能力强，充分利用了所有的基线相位差测量信息，解模糊的效果较好。但其对基线变化的适应能力差，且运算量较大，尤其是在基线个数多，雷达信号点数多的情况下运算量会大幅提高。在实际工程应用中要根据不同的需求选择解模糊方法。

[1]张永顺.雷达电子战原理[M].北京:国防工业出版社,2006.

[2]潘琳.干涉仪测向与相位差变化率定位技术[D].西安:西安电子科技大学,2009.

[3]谢东.干涉仪测向技术研究[D].成都:四川大学,2003.

[4]毛虎,杨建波,刘鹏.干涉仪测向技术现状与发展研究[J].电子信息对抗技术,2010,25(6):1-6

[5]赵国庆.雷达对抗原理[M].2版.西安:西安电子科技大学出版社,2012.

[6]任鹏,李建军,周彬,等.多基线干涉仪解模糊算法[J].电子信息对抗技术,2015,30(3):6-8.

[7]张智锋,乔强.低信噪比下相关干涉仪测向处理方法[J].舰船电子对抗,2009,32(12):103-106.

Offline Interferometer Defuzzification

TIAN Bing

(School of Electronic Engineering, Xidian University, Xi’an 710071, China)

A comparison is made between two commonly used defuzzification methods (baseline length and statistical phase variance) for linear interferometer DF where blur may result from cyclical phase ambiguity. Theoretical analysis and simulation are performed at different SNRs and short baseline spacings. The results show that at a low SNR the statistical phase variance method offers better defuzzification accuracy and stability, and signal adaptability than the baseline phase variance method; the change in short distance has great impact on the measurement errors by the statistical phase variance method.

interferometer; DOA; defuzzification; statistical phase variance

10.16180/j.cnki.issn1007-7820.2016.08.033

2015-11-19

田冰(1991-)，男，硕士研究生。研究方向：无源侦察-干涉仪测向。

TN953

A

1007-7820(2016)08-114-03