基于 FPGA 的水声信号数字下变频的实现

唐伟杰（中国船舶重工集团公司第七一五研究所，浙江　杭州 310012）

基于 FPGA 的水声信号数字下变频的实现

唐伟杰
（中国船舶重工集团公司第七一五研究所，浙江杭州 310012）

随着声呐信号处理技术的发展，其对系统的软、硬件资源要求越来越高。利用数字下变频技术，可极大地降低其信号处理资源要求。结合 Matlab，仿真研究整个下变频过程，验证分析水声信号数字下变频的正确性。在此基础上，应用 Verilog 语言移植算法到 FPGA 内部，在 Signaltap II 下观察过程变量及结果，并导入 Matlab 进行数据分析。该技术对于声呐信号处理具有实用价值，并已成功应用于某声呐设备。

声呐；水声信号；滤波；降采样；FPGA

0　引　言

在数字采集系统中，一方面希望信号采样时用尽可能高的采样率；另一方面在信号处理时又希望尽可能降低信号速率，以降低对信号处理器件的性能要求［1］。这两者看似矛盾的需求，在数字下变频技术的支持下，成为一个有机整体。在水声声呐系统的接收机中，也正不断借鉴其技术，对水声信号的数字下变频技术实现有实际应用价值。

1　基本原理

数字变频的概念是指把信号搬移到更高或者更低的载频上，可通过信号 x（t）与 1 个旋转向量相乘得到，即，其中 fc为载波频率。把基带信号搬移到该频点上就是上变频，将该信号从该频点搬移到基带则称为下变频。

1.1数字下变频

数字下变频器（DDC）主要由数控振荡器（NCO）、混频器、低通滤波器及抽取器等组成［2 - 3］。DDC 的核心部分是将 A/D 采样得到的信号与 DDC 中的数控振荡器（NCO）产生的本振信号混频，进行频谱搬移，得到零中频的基带复信号，分别为同相分量和正交分量。经过数字混频之后，此时信号的采样率仍然是ADC 采样频率，数据率可能较高，信号的带宽远小于采样频率，所以需要经过低通抽取滤波器降低信号采样率，完成了下变频的过程。DDC 的原理如图 1所示。

1.2数控振荡

数字控制振荡器（NCO）是产生一个给定频率信号的信号发生器，更确切的说是产生一个频率可变的正弦或余弦样本。

图 1　DDC 的原理框图Fig. 1　Schematic diagram of DDC

产生正弦或余弦信号样本最直接、最简便的方法是查表法［4］，即事先根据正弦或余弦波的各个相位计算好相应的值，并按相位角度作为地址存储各相位的正、余弦样本值。

1.3混频器

数字混频器是将原始采样信号与本振信号正、余弦量分别相乘，最终得到正交的信号［5］。自然界中物理可实现的信号都是实信号，其频谱具有共轭对称性。因此，对于一个实信号，只需正频或者负频部分就能完全加于描述。对于一个实的窄带信号：

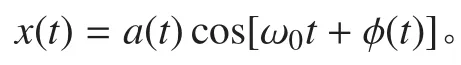
其解析信号可表示为：

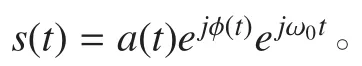
基带信号为解析信号的复包络，是复信号，既有正频分量又有复频分量。在数字信号处理中，常常采用数字混频正交变换来进行数字信号的正交分解，即将原始信号分别与正交本振信号和相乘，再通过低通滤波器实现。

1.4FIR 低通滤波

在数字下变频器中，关键的问题是数据抽取后的数字滤波。对于基带数据抽取，数字滤波器为低通滤波。数字滤波器的输入为，输出为，冲击响应为，有：

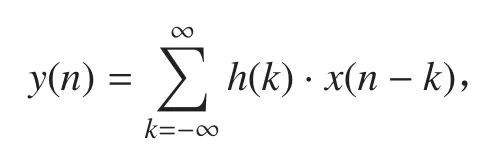
数字滤波器可以用，有限冲激响应（FIR）和无限冲击响应（IIR）滤波器 2 种形式［6］。FIR 滤波器是指冲激响应为有限个值的的数字滤波器，其频率响应为：

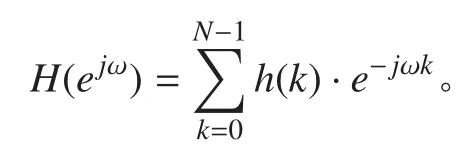
相比于 IIR 滤波器，FIR 滤波器具有线性相位、稳定性等特点，适于声呐中信号处理的要求，并且其设计相对成熟。常用的设计方法有窗函数设计法、频率采样设计法和等同纹波设计法等，其中窗函数设计法是最简单，也是最常用的设计方法。该方法是用一个FIR 滤波器的频率响应来逼近所要求的理想滤波器的频率响应：

常见的窗函数有矩形窗、三角窗、汉宁窗、布拉克曼和凯塞窗函数等。

1.5多速率信号抽取

在完成信号的基带搬移后，还需要降低数据率，以满足基带信号处理的要求，此为多速率信号处理过程要解决的问题。其最基本 2 个过程为抽取和内插，抽取就是降低数据率而内插为提高数据率［7］。

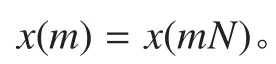
2　Matlab 功能仿真

上述各功能模块级联起来，形成一个下变频系统。在水声声呐系统中，信号频率较软件无线电中低很多，其高频声呐也只有千赫兹级，信号形式多为线性调频、单频等信号。

下变频中主要包括部分：混频和滤波。将输入信号与 NCO 产生的本振信号做乘法运算，输出运算结果，构成混频部分。而滤波部分是为滤除杂散的频率成分，得到预期信号。

2.1NCO 产生和混频器

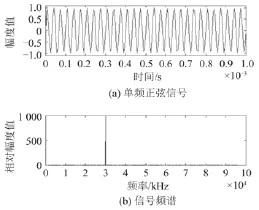
图 2　频率为 30 kHz 的正弦信号时频图Fig. 2　30 kHz Sine signal in time and frequency domain

NCO 本振信号频率为 24 kHz，采样率为 192 kHz，产生正交的正、余弦分量，与输入信号混频，进行频谱搬移。图 3 为正余弦分量信号时域波形，截取一定时间。图 4 为混频后的输出信号。

2.2FIR 滤波器

以汉宁窗函数作为 FIR 滤波器的滑动窗口，n = 50阶，混频后的数据通过 FIR 滤波器，得到的波形如 5图所示，可以看出其 I 和 Q 路信号的时域波形，并且分析得到频谱，符合理论计算。

2.3数据抽取

经数字 FIR 滤波滤除杂散频率，进一步以 6：1 抽取数据，以降低数据率，原采样率为 192 kHz，抽取后为32 kHz。在 Matlab 中，以该比例抽取数据，重组数据得到新的数据序列，如图 6 所示，可以看出其 I 和 Q路信号的时域波形，采样率明显降低，但其频谱成分不会改变。

图 3　本振信号 24 kHzFig. 3　24 kHz Sine and cosine signal

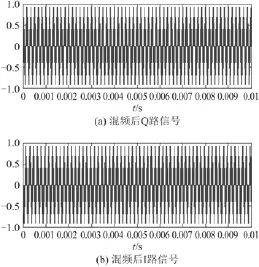
图 4　混频后的 I、Q 时域信号Fig. 4　I and Q singal after frequency mixing

图 5　FIR 滤波后的时频图Fig. 5　I and Q signal in time and frequency domain after FIR filter

3　下变频的 FPGA 实现

FPGA 芯片选择为 Altera 公司的 CycloneIII 的 EP3C120型号，芯片内部具有 119 k 的 LE 单元，288 个 18bit×18bit的乘法器，片内 RAM 有 3.88 kbits，系统的主时钟为50 MHz，应用 Verilog 语言编程 + IP 核的设计的设计方法。

图 6　数据抽取的时频信号图Fig. 6　I and Q signal in time and frequency domain after data decimation

3.1NCO 模块的实现

NCO 主要产生正交的正余弦分量，其实质是实现频率的合成，而直接数字频率合成（DDS）技术是一种全新的频率合成技术，具有频率分辨率高、转换速度快和相位连续等特点。在 EP3C120 的 IP 核库中，具有 DDS 模块，可以配置参数生成特定的输出信号。其模块如图 7 所示。

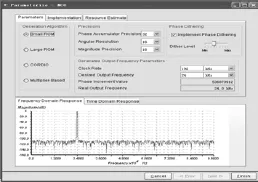
图 7　DDS 的配置参数示意图Fig. 7　DDS configuration diagram

其中 clk 为输入时钟 192 kHz，phi_inc_i 为参数值，决定输出信号的频率，字长为 16 bit。图 8 中dsine 和 dcosine 是在 signaltap II 中 DDS 的输出信号本振信号。

3.2混频器的实现

混频的实质是将中频信号的采样值与本振信号进行乘法运算，因此混频器可用乘法器代替。在EP3C120 中，内部有一定的乘法器资源，在 Quartus 编程设计时例化乘法器宏模块。

设 data_in1 为输入信号 30 kHz，作为乘法器的输入变量，dsine 为 24 kHz 的本振正弦信号，作为乘法器的另一变量。在 FPGA 内部嵌入式逻辑分析仪 signaltap中，各变量如图 9 所示，其中的 data_out4 即为乘法器的输出结果，把相应的变量值保存为 tbl 数据格式，导入 Matlab 中，分析其混频后变量 data_out4 的频谱，如图 10 所示。

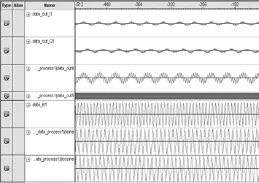
图 8　Signaltap 中 DDS 输出信号Fig. 8　DDS outputs in signaltap II

图 9　混频后的 signaltap 中的信号量Fig. 9　Signals in signaltap after multiplication

图 10　混频后的频谱图Fig. 10　The frequency spectrum after multiplication

3.3FIR 低通滤波的实现

在混频器完成频带的搬移之后，从频谱图 13 可看出存在着其他频率成分。Cyclone 系列 FPGA 支持 FIRII 型滤波器 IP 核，设置低通滤波为 50 阶，选择Hanning 窗函数，截止频率为 7 kHz。图 11 是经过 FIP滤波和数据抽取后相关信号量的示意图，其中 dataI 和dataQ 是滤波器的输出。图 12 是经滤波后的信号频谱示意图，比较图 10 和图 12，能很好地滤除带外的分量。

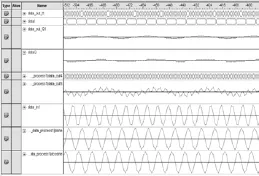
图 11　滤波及数据抽取后的信号量Fig. 11　Signals in signaltap after filter and decimation

图 12　滤波后的信号频谱图Fig. 12　The frequency spectrum after filter

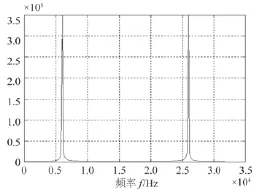
图 13　数据抽取后的频谱图Fig. 13　The frequency spectrum after data decimation

3.4数据的抽取

设计数据抽取器，以 6：1 的系数抽取，原始数据采样率为 192 kHz，抽取后数据率为 32 kHz，基带信号为 6 kHz，仍满足采样定理。在 FPGA 中，将数据信号进行同步时钟的 6 分频，然后利用该时钟去采样得到的新序列数据即为抽取后的信号。如图 11 所示，其中data_out_I1 和 data_out_Q1 为抽取前数据，dataI 和dataQ 为抽取后正交、同相分量。可以看出其波形的正确性。在 Matlab 中频谱分析如图 13 所示，分析其频谱为 6 kHz，与理论上的数字下变频仿真一致。

4　结　语

水声信号数字下变频的实现，实现了信号的基带频谱搬移、系统处理数据率的降低，因此大大降低了对信号处理机处理能力的要求。本文所设计的模块已经应用到某水声声纳设备的前置预处理分机中，假设原始信号频率为 30 kHz，采样率为 192 kHz，数据 16位，50 个通道，则数据率为 16 bit×50×192 kHz = 150 Mb/s，下变频后的基带信号频率为 6 kHz，采样率为 32 kHz，则数据率为 16 bit×50×32 kHz = 25 Mb/s，经整机联调测试，以及湖试等验证功能的正确性。

［1］曹李秋. 软件无线电数字下变频 FPGA 实现的研究［D］. 武汉：武汉理工大学，2006.

［2］高亚军. 基于 FPGA 的数字信号处理［M］. 北京：电子工业出版社，2012：121-130.

［3］陈东坡. 数字下变频电路的 FPGA 实现［D］. 西安：西安电子科技大学，2009.

［4］周俊峰，陈涛. 基于 FPGA 的直接数字频率合成器的设计和实现［J］. 电子技术应用，2002，28（8）：34-36.

［5］胡跃，张正鸿. 基于 FPGA 的数字正交混频变换算法的实现［J］. 国外电子测量技术，2007，26（5）：9-11，14.

［6］奥本海默 A V，谢费 R W，巴克 J R. 离散时间信号处理［M］.刘树棠，黄建国，译. 西安：西安交通大学出版社，2007：352-412.

［7］西瑞克斯（北京）通信设备有限公司. 无线通信的 MATLAB 和FPGA 实现［M］. 北京：人民邮电出版社，2009：90-97.

［8］胡广书. 数字信号处理理论、算法与实现第3版［M］. 北京：清华大学，2012：355-363.

The implementation of digtal down conversion of underwater acoustic signal with FPGA

TANG Wei-jie
（The 715 Research Institute of CSIC，Hangzhou 310012，China）

With the development of sonar signal process，more and more software or hardware resources are required. It can greatly reduced just use Digtal Down Conversion（DDC）. In the paper，simulation was done to study the DDC of Underwater Acoustic Signal in Matlab，and results were given and analyzed. Then the digtal signal processing was programmed by Verilog in FPGA. Variables and results were checked in Signaltap II and analyzed in Matlab. This technology have practical value to signal processing of Sonarand have been sucessed applied in the Sonar system.

sonar；underwater acoustic signal；filter；down sample；FPGA

U666.7

A

1672 - 7619（2016）08 - 0090 - 05

10.3404/j.issn.1672 - 7619.2016.08.019

2015 - 12 - 12；

2016 - 01 - 06

国家“863”计划 资助项目（2011AA09A107）

唐伟杰（1982 - ），男，硕士研究生，工程师，主要从事水声信号预处理。