基于粒子群算法的城市接驳公交网络优化调度方法

邢 雪

（1.吉林化工学院信息与控制工程学院，吉林吉林 132022；2.吉林大学交通学院，长春 130022）

基于粒子群算法的城市接驳公交网络优化调度方法

邢 雪1，2

（1.吉林化工学院信息与控制工程学院，吉林吉林 132022；2.吉林大学交通学院，长春 130022）

为提高公共交通分担能力和解决轨道交通与交通出行起讫点之间的公共交通接驳优化调度问题，提出了轨道与公交的接驳公交网络优化模型.模型主要考虑不同接驳站点在不同时间对轨道交通和交通出行起讫点之间的接驳需求建立多目标模型.分析选用粒子群算法对所建立的多目标优化模型进行分析求解，比较了在轨道接驳需求下多种车队规模的调度线路、时刻安排状况，得到轨道线路邻近区域内接驳网络的优化调度，当车队规模在定值时即可满足接驳轨道交通的换乘需求，优化调度使得平均满载率显著下降，另外，验证了接驳公交网络基于粒子群算法的优化调度可有效降低营运消耗.

接驳公交优化；多目标约束；粒子群算法；网络优化模型

随着城市规模的不断扩展，搭乘公共交通是城市中多数居民主要的出行方式，在规模较大的城市中，常规公交和轨道交通是城市公共交通架构的主体部分，接驳公交专线则以接驳轨道站点乘客为目的，兼顾其他公共交通线路功能.由于常规公交线路的主导优势（灵活方便、布设范围广），接驳公交可以充分利用轨道交通并合理完善存在的不足，填补我国轨道线网密度小的缺点，为轨道交通站点提供有效的集散.在接驳公交的研究方面，Chien等给出了与发车时刻相协调的接驳公交线网布设优化方法［1］；Martins和Pato在对接驳公交线路数量以及布设方式进行分析的基础上提出了一种线路布设寻优的算法［2］.2006年，研究学者对公交接驳线网进行优化分析，其中运用了蚁群分析方法和启发式遗传算法［3-4］，也有学者使用启发式遗传算法对接驳公交网络优化的N-P难问题进行求解［5］.国内对轨道交通与常规公交衔接的研究主要基于评价方法［6-10］.我国的交通规模与国外还存在差距，轨道交通网络还不够成熟［11］.因而，结合我国公交的特点来研究与轨道交通衔接的理论方法是十分必要的.本文主要研究城市轨道接驳公交的线网优化和线路合理调度，以轨道交通作为主要干线，常规公交作为主要接驳线路的合理公交线网，从而实现路网有效换乘.

我国的轨道交通还处于发展阶段，当轨道线路建成之后将打破之前正常运营的常规公交线路，这便需要对机动灵活的常规公交线网进行调整，从而保证轨道交通与交通出行起讫点之间接驳的高效性.

1 接驳公交网络优化模型构建

1.1接驳候选公交线路集合的确定

接驳公交线路是轨道投入运营后形成的一种复杂、特殊的公交线路，其主要作用:一是为满足轨道交通站点客流的需要；二是为其站点的客流集散提供更好的服务.根据接驳公交线路的特点及作用，其线路集合的原则为:接驳公交线网服务区域的每条接驳公交线路只单纯为一个特定的轨道交通站点服务，确定候选线路前将轨道交通站点设为中心，并得出为该站点提供接驳服务的其他接驳公交的候选站点集合.当接驳公交站点和轨道交通站点的间距比允许的最大可接受距离小的时候，就可确定接驳公交线路的候选集合.此时的候选线路集合的所有站点均小于接驳公交线路的最大允许长度.在给定轨道车站以及为其服务的公交站点集后，接驳公交的候选线路的候选集合确定过程如图1所示.

1.2接驳公交网络模型优化的目标

1）接驳公交最大化有效载客量

接驳公交网络在空间结构上的局限性决定了接驳公交网络不能对所有实际需求点提供服务.接驳公交线网的初衷是为出行者在轨道交通与交通出行起讫点之间提供接驳服务.而作为两者间的衔接网络，在接驳短途中不存在换乘行为，其服务均为直达方式，则接驳公交有效载客流量PF的最大化如下:

式中:S表示所有接驳公交需求点的集合；s表示接驳公交需求点（s属于S）；R表示所有接驳公交候选线路的集合；r表示候选的线路（r属于R）；qs，j表示从第j次接驳公交线网下车后，去往轨道车站s的接驳公交需求（s属于S）；Er，s表示接驳公交候选线路与接驳公交侯选站点通过关系；Gr表示接驳公交网络与接驳公交候选线路的关系，当接驳公交线路r被选入接驳公交网络时取值为1，否则为0，其中r属于R.

2）乘客时间消耗（乘客等车时间消耗、乘客乘车时间消耗）最小化

由于轨道交通具有规律性特征，可以定义接驳公交的班次运营时间为轨道交通运营班次到站时间加上接驳乘客的候车时间，从而保证轨道交通换乘到接驳公交的候车时间为最小.所以，接驳乘客从轨道交通站点到接驳公交站点的时间和乘车时间构成了本模型的时间消耗.模型中为统一假设，同一化所有接驳乘客的时间花费，且总班次运营时间与接驳乘客成本成正比关系，则接驳乘客的时间消耗为

乘客换乘等待时间消耗为

式中Zr，si，j表示乘客从第j次轨道下车，选择换乘接驳公交线路r的第i车次，此车次的目的地是接驳公交车站s时取值为1，否则为0.其中r属于R，s属于S.

乘客的乘车时间消耗为

式中dr，s表示在接驳公交线路r上接驳公交首站与接驳公交站点s之间的距离.

3）接驳公交网络的营运消耗最小化

公交营运就必然有相应的营运消耗，则根据之前的研究［12］可知，公交营运消耗与公交营运距离或者公交营运时间成比例关系.本模型选取营运消耗与营运时间的关系为

式中:fr表示接驳公交线路r的发车频率；lr表示接驳公交线路r的总长度；v表示接驳公交车辆平均的运行速度.

1.3接驳公交候选线路集合的生成算法目标函数为

模型约束条件为:

1）任何接驳公交车站最多服务于一条接驳公交线路.

2）接驳公交线路被选为接驳公交网络后，出行者才可以选择此线路.

3）当接驳线路r通过车站s时，从轨道车站出发到该接驳公交车站为目的的乘客方可选择线路r.

4）接驳线路r的发车时间间隔要介于最小发车间隔与最大发车间隔之间.

式中:hmin表示接驳公交所允许的最小发车间隔；hmax表示接驳公交所允许的最大发车间隔；tr，i表示候选线路r上的接驳公交第i次接驳公交车辆的发车时间；tj表示第j次轨道交通到达站点的时间.

5）接驳公交所需的车辆总数要在接驳公交供给的范围之内.

式中:Nr表示第r条接驳公交线路上公交车辆供给量；Nmax表示最大接驳公交供给限值.

6）接驳公交满载率

式中:pmin表示接驳公交所允许的最小满载率；pmax表示接驳公交所允许的最大满载率；qr，max表示接驳公交候选线路r断面最大客流量；c表示接驳公交车辆容量.

2 基于粒子群算法的模型求解

2.1粒子群优化算法

粒子群优化算法（PSO）［13］源于复杂适应系统（CAS），是从生物种群行为特性中得到启发并用于求解优化问题.用PSO模拟飞行过程，其中每个粒子所经历过的最好位置就是粒子本身找到的最优解.而生物群落整体所经历过的最好位置，就是目前整个群落找到的最优解.在实际流程中通过适应度值（fitness value）来评价粒子的优劣程度，群落中的粒子通过对上述2个最优值的评价不断自我更新，从而衍生出新一代群落.

实际上优化算法（如模拟退火算法、蚁群算法、遗传算法等）由于各自的适应性不同，优化模型时的选择也不同，如:模拟退火算法在初始的条件设置较高时，优化过程也相对较长；蚁群算法比较复杂，求解过程长，容易出现停滞的现象.遗传算法迭代过程是“生成+检测”的过程，后期的搜索速度缓慢，实现过程依赖设置的参数.与此相比，PSO在解决多目标优化问题上具有很大的优势.PSO优势搜索具有高效性，在过程中逐步调整，有利于在适应度下求最优解；另外，通用性较好，易与传统方法结合，并适合多种类型目标函数和约束条件的设置，可更好地改进自身的局限性.

2.2接驳网络优化的PSO优化求解流程

多个目标共同最优存在的可能性微乎其微，即唯一的全局最优解不存在.但在优化的过程中可能存在下述的解，即不针对全部目标函数进行最优化评判，而是在一定比例下保证多目标中一个或几个不至于劣化，求得解空间的非劣最优解.

接驳网络优化的PSO优化流程如下:

1）初始化粒子群

给定群体规模N，以所有候选接驳站点数目初始化粒子群，即随机选定每个粒子的位置Xi（描述为接驳线路下候选接驳站点经纬度坐标）、速度Vi（描述为接驳线路下的调度序列）.

2）初始化适应度参数

为粒子适应度、最佳适应度、最佳位置和粒子群中最佳粒子等参数设定初始值.

3）给定粒子的适应度度量方式

用目标函数给定每个粒子的适应度度量方式，应用惩罚函数来表示它的适应度

式中:参数θ1为惩罚因子（不满足可用车队大小限制）；参数θ2为惩罚因子（不满足线路长度限制）；参数θ3为惩罚因子（不满足满载率限制）；参数θ4为惩罚因子（不满足发车间隔限制）.

4）给定速度-位移模型操作算子

飞行经历操作以接驳线路下的调度序列为速度Vi，进而更新位置粒子位置，计算当前粒子适应度.

5）设定基于目标函数的粒子自身极值算子

如果当前粒子适应度好于当前粒子最佳适应度，则更新当前粒子最佳适应度并更新当前粒子最佳位置；如果当前粒子最佳适应度好于模型的最佳粒子适应度，则更新模型的最佳粒子适应度及位置.

6）判断是否满足中止条件

如满足中止条件则退出；否则返回步骤3）.

计算过程中如判断终止条件满足则终止，在此算法过程中有2种终止条件，只要其中一个满足即终止操作.

第1种终止条件:达到初始给定的运算代数，即t=T.

第2种终止条件:

式中:Z′（t）属于第t次迭代最佳个体的适应值；ε为无限小的正实数.

3 算例分析

长春轨道某站点附近公交站点的具体位置分布如图2所示，其中标识O点表示轨道交通站点，标识a～m则表示附近具有接驳需求的公交站点.将接驳公交站点或者接驳需求点标识为a～m，节点之间的距离用其路段附近的数字来表示（单位:km）. 图3中给出了所需接驳的客流总量，分别给出了轨道车辆到达站点时刻和不同需求点的总接驳量（由轨道站点下车直至各个需求点）.

式（13）中的车辆惩罚因子θ1、发车间隔惩罚因子θ4均取极大正数值；由于线路长度限制则惩罚因子θ2实际估算为0.相应线路r的满载率惩罚项θ3表示为

式中:pmin、pmax表示最小满载率和最大满载率，通过采集实际运营数据获得pmin、pmax，分别取值0.45、0.95；Pr表示线路r的满载率；μ表示惩罚因子，参数值取1 000.

实例中其他参数遵从以下设定:接驳公交车辆的平均速度为16 km/h；按常规取hmin为6 min，hmax为30 min；φ取基本单位值；多目标规划权重系数ε、k、λ（按接驳公交有效载客量、乘客时间消耗和接驳公交网络的营运消耗统计值的数学期望比例）取值分别为0.20、0.35、0.35.

优化比较轨道交通附近接驳公交线路（如表1所示），在实际运营下比较选取5种不同的车队规模的营运情况（线路时刻选取、可行线路最优分配），车辆的容量取值为60人/辆.在可用车队规模变化过程中，运营成本随车队规模正比变化，乘车成本随车队规模增加而降低，模型选取的具体参数如乘客成本、车队营运消耗等参数均参考文献［12］.

表1　轨道交通附近接驳公交线路Table 1 Feeder bus routes near the rail transit

经算法优化，比较不同时刻表及不同公交运力下的不同接驳线路公交满载率，结果表明:

1）由于接驳公交的载客量随接驳公交网络的线路组成和时刻表变化而改变，充分体现了接驳载客量相对于公交的弹性需求.

2）在弹性需求下，车队可用车数目偏小时（即供给可用车辆不足），可导致出现不同程度的接驳公交乘客状态的拥挤现象，公交运输能力的局促性会造成乘客焦虑.

3）当可用车队规模不断递增（线路组合随之不同）时，线路的时刻表相应变化，即车辆供给规模不同的条件下，应充分考虑线路和发车时刻的协调调度加以优化.

4）在车队规模不断递增，由不足到接驳充足的过程中，可供车辆数、优化调度线路及线路时刻变化如表2所示.线路的发车频率随可用车数目增多而减小，乘客等待时间也随可用车数目增多明显减小，平均满载率有显著改善，表现为下降趋势.

5）由于接驳公交承担的成本随运营车辆的数量正比变化，运营服务的水平也与之正比提升，相应吸引了更多乘客选择接驳公交，与此相对应的接驳需求量必然增多.在多车队模型下比较，当车队规模增加到一定量值（如表2中接驳车队可用车辆为11辆）之后，算法优化得到相应的乘客成本、接驳营运状态和接驳公交OD与可供车量为11辆没有大幅度变化，说明在接驳网络优化调度时，可通过算法优化出车队规模的某个定值，即可满足接驳轨道交通的换乘需求.

6）在多车队规模下优化迭代次数与优化选择后将接驳公交网络的营运消耗关系图进行比较，由于调度达到11辆即可满足接驳需求，因而只针对车队规模为5、7、9和11辆时的状态进行分析，如图4所示.图中（a）～（d）分别表示5、7、9和11辆时随优化迭代次数增加优化选择后接驳公交网络的营运消耗曲线，说明接驳公交网络基于粒子群算法的优化调度可有效降低营运消耗，分别平均降低24.14％，并在多目标控制下的解空间中优化得到非劣最优解.

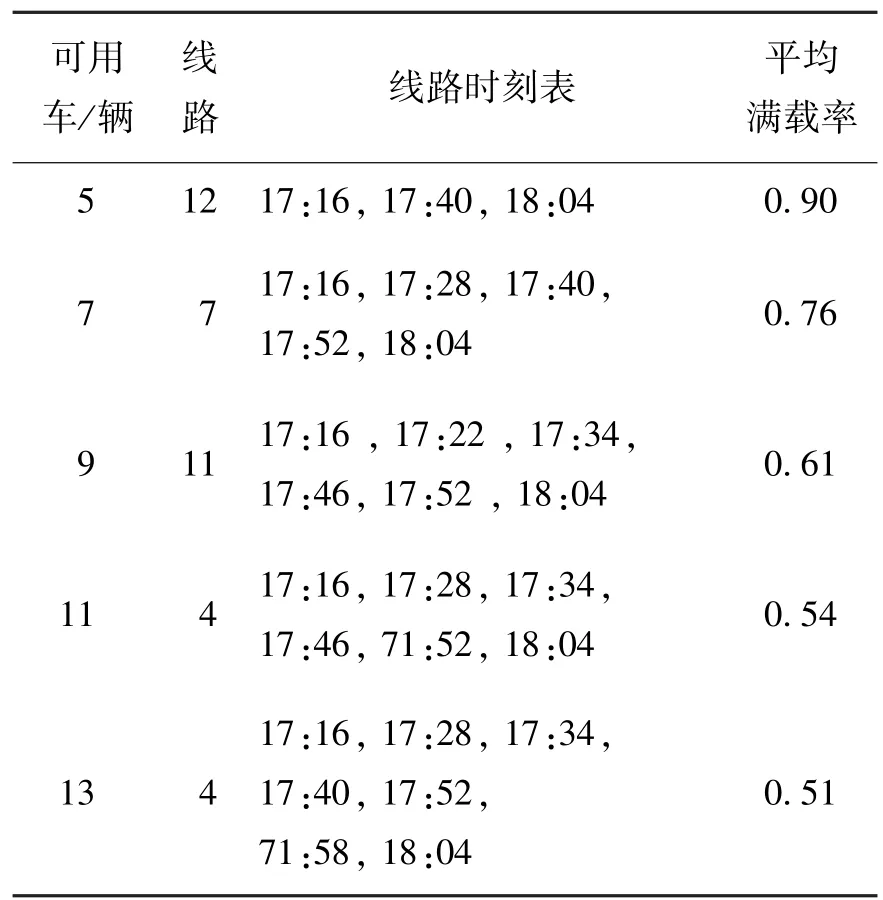
表2　不同车队规模下优化结果比较Table 2 Comparison of optimization results under different team

4 结论

1）针对解决轨道交通与城市接驳公交网络的优化调度问题，在轨道交通乘客密集时段接驳需求下，采用粒子群优化方法，以接驳公交有效载客量的最大化、乘客时间消耗（乘客等车时间消耗、乘客乘车时间消耗）最小化、接驳公交网络的营运消耗最小化为多目标进行了具体的算例分析.通过仿真结果，分析了在不同公交车队规模下调度的变化情况，比较了在接驳需求下多种车队规模的调度线路、时刻安排状况，得出了在接驳网络优化调度时，车队规模稳定在定值即可满足接驳轨道交通的换乘需求，并验证了粒子群算法的高效优化效果.

2）本文对轨道交通邻近的接驳公交优化调度模型进行了分析，模型对大规模路网具有一定适应性，而对实际路网的适应性还有待进一步研究.另一方面考虑到未来交通客运一体化的大趋势，对解决轨道公交一体化无缝换乘方面的研究还有待深入.

［1］CHIEN S，YANG Z W，HOU E.Genetic algorithm approach for transit route planning and design［J］.Journal of Transportation Engineering，2001，7:200-206.

［2］MARTINS C L，PATO M V.Search strategies for feeder bus net-work design problem［J］.European Journal of Operation Research，1998，106:425-450.

［3］CHOWDHURY M，CHIEN S.Dynamic vehicle dispatching at intermodal transfer station［C］∥Transportation Research Board Natl Research Council.Transit Planning，Intermodal Facilities，and Marketing.1753.Washington D.C:Transportation Research Record，2001:61-68.

［4］SHOAIB M D，CHIEN S I J.Optimization of transfer coordinationforintermodaltransitnetwork［C］∥Transportation Research Board Natl Research Council. Transit Planning，Intermodal Facilities，and Marketing. 1762.Washington D.C:Transportation Research Record，2001:89-94.

［5］KUAN S N，ONG H L，NG K M.Solving feeder bus network design problem by genetic algorithms and ant colonyoptimization［J］.AdvancesinEngineering Software，2006，37（6）:351-359.

［6］纪雪艳.城市轨道交通换乘站综合评价研究［D］.北京:北京交通大学，2009. JI X Y.Research on the comprehensive evaluation of urban rail transferstation［D］.Beijing:BeijingJiaotong University，2009.（in Chinese）

［7］王卫平.常规公交与城市轨道交通衔接理论方法与评价研究［D］.广州:华南理工大学，2011.WANG W P.The study on the transfer method and evaluation theory between conventional bus and rail transit ［D］.Guangzhou:South China University of Technology，2011.（in Chinese）

［8］丑洋.轨道交通与常规公交站点协调换乘评价研究［D］.西安:长安大学，2012. CHOU Y.Evaluation study on station transfer coordination of rail transit and conventional bus［D］.Xi'an:Changan University，2012.（in Chinese）

［9］胡启洲，常玉林.城市公交线网多目标优化的建模及其求解［J］.江苏大学学报（自然科学版），2003，24 （6）:88-90. HU Q Z，CHANG Y L.Model for multiple objective optimization about urban public traffic line network［J］. Journal of Jiangsu University（National Science Edition），2003，24（6）:88-90.（in Chinese）

［10］孙杨.城市轨道交通新线投入运营下常规公交线网优化调整方法研究［D］.北京:北京交通大学，2012. SUN Y.Methodology of bus network optimization and adjustment under the operation of urban new rail transit line［D］.Beijing:Beijing Jiaotong University，2012.（in Chinese）

［11］建设部.关于优先发展城市公共交通的意见［DB/ OL］.［2015-08-10］.http:∥www.cin.gov.cn/city/ other/2004031802.htm，2004.

［12］曹玮.城市轨道交通与接运公交换乘模型优化研究［D］.西安:长安大学，2013. CAO W.Study on the optimization model of shuttle between urban rail transit and feeder bus［D］.Xi'an: Changan University，2013.（in Chinese）

［13］张利彪，周春光，马铭，等.基于粒子群算法求解多目标优化问题［J］.计算机研究与发展，2004，41 （7）:1286-1291. ZHANG L B，ZHOU C G，MA M.Solutions of multiobjective optimization problems based on particle swarm optimization［J］.Journal of Computer Research and Development，2004，41（7）:1286-1291.（in Chinese）

（责任编辑 梁 洁）

Feeder Bus Network Optimization Scheduling Method Based on Particle Swarm Optimization

XING Xue1，2
（1.College of Information and Control Engineering，Jilin Institute of Chemical Technology，Jilin 132022，Jilin，China；2.College of Traffic，Jilin University，Changchun 130022，China）

A feeder bus optimization scheduling model was put forward to improve the public transport sharing ability and solve bus optimization scheduling problem between rail transit and transportation origin destination in regular public transport.Different transportation demands between rail transit stations and transportation origin destination stations in different times were mainly considerate in the model，and then a multi-objective programming model was established.The multi-objective optimization model by using particle swarm optimization was analyzed and the optimal results under different situations were compared.Results show that the fixed value of buses in the team of the network optimization scheduling can meet the requirements of passengers in adjacent areas.The average load ratio is reduced significantly by using optimal operation.The viability of cost reduction of the proposed optimization model is also demonstrated.

feeder bus optimization；multi-objective constraints；particle swarm optimization；network optimization model

U 491

A

0254-0037（2016）09-1385-07

10.11936/bjutxb2015110058

2015-11-18

国家科技支撑计划资助项目（2014BAG03B03）

邢 雪（1983—），女，博士研究生，主要从事智能交通运输系统方面的研究，E-mail:patricia_xx@126.com