一种基于图像集合的三维重建方法

北京航空航天大学计算机学院　林连庆　杨志刚

一种基于图像集合的三维重建方法

北京航空航天大学计算机学院林连庆杨志刚

设计并实现了一整套基于图像集合的三维重建技术。首先对输入的多幅图像提取特征点，然后将这些特征点进行匹配，接着迭代运行从运动恢复结构的优化算法，得到相机参数以及稀疏的空间点云信息，最后利用多视图立体重建方法得到稠密的空间点云模型，完成对目标的三维重建。实验结果表明，本文采用的方法不需要特定的设备，无需人工干预即可自动重建出正确的被观测目标的三维模型。

三维重建；特征点提取与匹配；从运动恢复结构SFM；多视图立体重建PMVS

1.引言

众所周知，在我们生活的现实世界中，周围环境和物体都是三维的客观存在，这是人类通过双眼获得的视觉信息。如何让机器像人一样感知、分析、理解、记忆以及再现外界的三维场景，是计算机视觉［1］研究的热点课题之一，即通过运用计算机和数字传感设备来模拟人类视觉功能，获取被观测目标的三维几何信息，这个过程就是三维重建。

基于计算机视觉的光学三维重建方法可以分为主动式和被动式两大类［2］。主动法需要人为对目标场景施加特定的照射光源，根据光束模式和物体表面的反射特性，利用光学原理及相关特性获取待重建目标高精度的三维信息，主要包括结构光和激光扫描等方法。由于需要比较复杂且造价高昂的专用设备，不适合室外大型场景，使得其应用受到限制。被动法只利用在自然光照条件下拍摄的图像，就可恢复出相机的运动和场景的结构，具有简单易行、成本低廉、适应性强、灵活度高等特点，近年来越来越受到研究重视。随着数码相机、摄像机、手机等硬件成像设备的普及，人们可以随时随地拍摄得到想要的图片，再利用基于图像的三维重建技术，直接根据这些图片恢复物体的三维几何结构，甚至构建出非常逼真的三维模型，在日常的生产生活中具有广泛的应用价值跟前景。

2.三维重建的原理和流程

基于图像的三维重建是摄像机成像过程的逆过程，主要原理基于光学中的针孔成像模型，即：三维世界空间的点与二维成像平面上的投影点满足中心射影的数学模型，如公式（1）所示，

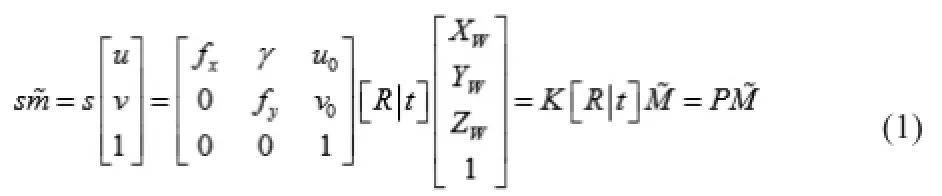
本文基于图像集合进行三维重建的具体流程如图1所示。主要步骤为特征提取与匹配、稀疏3D重建和稠密3D重建，本文将在后续内容进行详细介绍。

3.特征提取与匹配

本文采用SIFT特征描述子结合Harris算法来进行特征点提取，在SIFT特征点的基础上加入了物体的角点特征，二者取长补短，使得重建结果在细节上更加突出，更加接近真实物体。

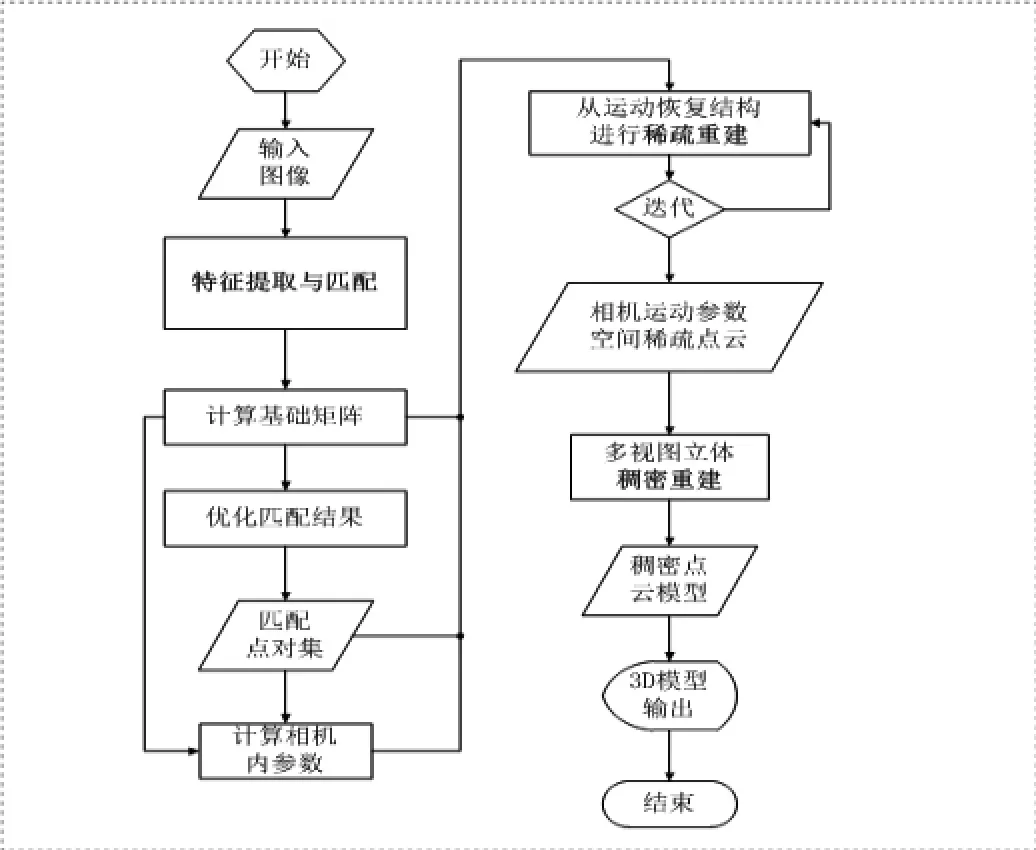
图1　基于图像集合的三维重建流程图

3.1SIFT算法

SIFT算法通过建立图像的多尺度空间，在不同尺度下检测到同一个特征点，确定特征点位置的同时确定其所在尺度，以达到尺度抗缩放的目的，剔出一些对比度较低的点以及边缘响应点，并提取旋转不变特征描述子以达到抗仿射变换的目的。主要计算步骤如下：1）尺度空间极值检测；2）关键点的定位；3）确定关键点的方向；4）生成特征点描述子。

由于SIFT特征描述子是一个128维的向量，可以采用基于欧式距离的最近邻匹配算法（Nearest Neighbor-NN）完成粗匹配，其过程是：对图像I1中的每个特征向量a，在图像I2中利用kd-tree进行搜索，查找I2所有特征点中与a对应的最近邻特征向量b以及次近邻特征向量b’，如果最近邻除以次近邻的距离比值小于某个给定的比例阈值，即，则b为a的匹配，否则认为a在I2中没有匹配。实验中T的取值为0.6。

3.2Harris算法

Harris角点提取是一种基于图像灰度梯度的检测方法，由于自相关函数描述了局部图像灰度的变化程度，将自相关函数的近似Hessian矩阵作为Harris算子，表达式如下：

Harris角点探测器的响应函数为：

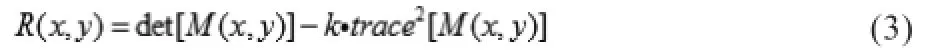
最后以每个特征点为中心，选取大小为（2n-1）×（2n-1）的灰度窗口称为特征点的邻域窗（实验中n=7），利用归一化互相关匹配算法（Normalized Cross Correlation， NCC）完成角点的初始匹配，设m1、m2分别为图像I1和I2中待匹配的两个角点，本文采用的相似度计算公式如下：

公式中，I（x，y）代表图像I在像素（x，y）处的灰度值，为邻域窗内的灰度平均值。

3.3基于RANSAC算法优化匹配

优化过程利用基础矩阵计算特征点到对应极线的垂直距离作为约束（小于1.5个像素），将只有一个方向或者两个方向都不满足约束关系的匹配，视为虚假匹配，予以剔除。求解基础矩阵采用的是改进的8点法［3］。本文基于RANSAC算法实现对基础矩阵的鲁棒估计，通过对外点（outlier）加以限制，从数据中找到内点（inlier），根据最大内点数和最小误差方差，选择最优的参数模型。

为了提高计算效率，本文采用改进的RANSAC算法：在对每个模型参数检验前，先随机抽取少量的数据对模型进行预检验，如果预检验通过，则继续在全部数据中进行模型评估，如果没有通过预检验，则放弃后面的评估过程。

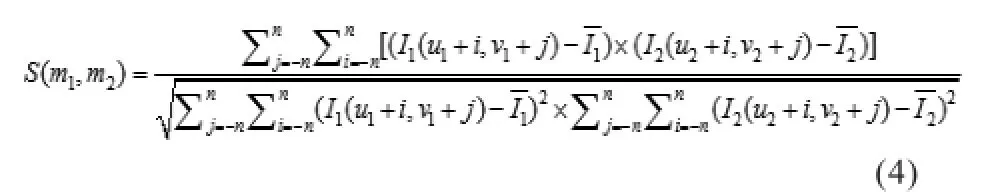
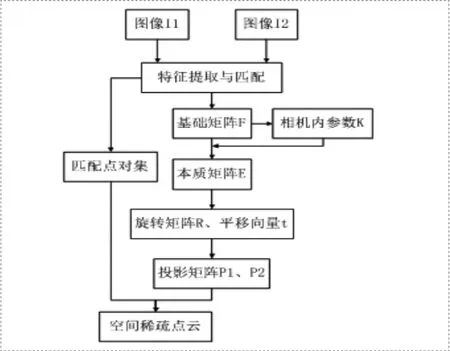
图2　两幅图像间三维重建流程图

4.稀疏3D重建

本文采用从运动恢复结构（Structure From Motion， SFM）［4］的方法基于图像集合重建目标的三维模型。SFM方法从两幅图像的匹配和重建开始，通过迭代逐渐增加新的图像，直至重建整个图像集合。通过两幅图像进行三维重建的大体步骤如下：在获得两幅图像间的匹配点对后，根据基本矩阵F求解Kruppa方程［5］，得到摄像机内参数K；同时根据基本矩阵计算本质矩阵E，对本质矩阵进行SVD分解得到摄像机的运动参数［6］——旋转矩阵R和平移向量t；然后由内外参数得到投影矩阵P；最后按照公式（1），由每对匹配点联立方程，求解出空间离散点在相差一个尺度因子下的三维坐标，生成空间稀疏3D点云。流程图如图2所示。

SFM将前两幅图像的重建结果作为一个初始结构，利用光束法平差［7］对其进行优化，然后在此基础上每次从图像序列中选择一副新的图像加入此结构，重复如下的迭代过程：

1）在新增图像中找到已存在于当前结构的特征点，根据其与前面已重建三维点的对应关系，采用RANSAC算法求出新增图像的投影矩阵；

2）根据计算出的投影矩阵对新增图像进行重投影，去除误差过大的特征点；

3）重建新增图像与前一幅图像的匹配点对中未被重建的特征点对；

4）对现有的结构进行更新；

5）通过光束法平差优化，同时对重建结果的三维结构和相机参数提供整体最优解。

5.稠密3D重建

为了得到更加真实、准确的目标重建模型，本文在稀疏重建的基础上，采用基于面片的PMVS（Patch-based Multi-view Stereo）准稠密算法［8］，该算法利用区域增长原理，输出具有方向的小矩形面片密集集合，由此产生稠密的三维点云模型。PMVS算法主要包括匹配-扩展-过滤三个步骤：

1）匹配。首先进行初始特征匹配，本文利用前面稀疏重建生成的结构作为潜在面片的初始值建立面片模型，通过光照一致性约束进行优化，得到一系列稀疏面片以及对应的图像区域，以此作为种子；

2）扩展。利用相邻面片具有相似的法向和位置的特性，扩展初始匹配到已经存在面片的邻近空挡区域，并进行优化更新，得到比较稠密的面片序列；

3）过滤。利用视觉一致性约束构建滤波器，去除位于观察物体实际表面之前或之后的错误匹配。

本文实验通过迭代将上述扩展和过滤步重复执行3次，并在扩散过程中加入几何空间约束，即同时考虑到四周相邻面片对于扩展面片的影响，沿着NCC增大的方向进行匹配传播。由于通过前面算法得到的初始种子匹配点对比较稳定和可靠，并加入了上述对PMVS算法的改进，使得用较少的图像序列即可生成鲁棒、精确的几何估计，得到高稠密的三维点云模型，实现对目标的三维重建。

6.实验结果

实验使用iPhone6（焦距长度4.15mm）手机围绕实验的人体头部雕塑拍摄了20幅图像，其中一幅如图3（a）所示，图像像素为2448 ×2448，通过自标定实际算得相机的焦距为2669.368像素。采用C++ 与MATLAB混合编程对上述算法进行实现，实验结果如下：图3（b）为SFM重建出的3D稀疏点云，共计得到5174个稀疏点；图3（c）为利用改进的PMVS算法重建出的稠密3D点云，共计1409503个稠密点；图3（d）为根据稠密3D点云重建的三角网格曲面模型。

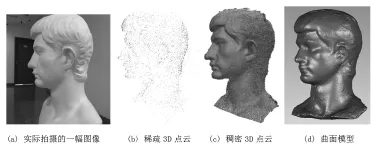
图3　头部雕塑模型重建实例

7.结束语

本文设计并实现了一整套基于图像集合的三维重建技术，通过对输入的多幅图像进行特征点提取、匹配和优化，根据计算出的基础矩阵，迭代运行从运动恢复结构的优化算法，得到相机参数以及稀疏的空间点云信息，最后利用多视图立体重建方法得到稠密的空间点云模型，完成了对目标的三维重建。实验结果表明，本文采用的方法不需要特定的设备，无需人工干预即可自动重建出正确的被观测目标的三维模型。后续还要对算法进行相关改进，例如增加图像预处理、输入更多先验信息、加入鲁棒性策略等等，进一步减低算法的计算开销，同时减轻误差累积效应，使重建结果更加完整逼真。

［1］马颂德，张正友.计算机视觉——计算理论与算法基础［M］.北京：科学出版社，1998.

［2］Maxime Lhuillier，Long Quan.A Quasi-Dense Approach to Surface Reconstruction from Uncalibrated Images.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005.

［3］Richard I.Hartley.In defense of the8-point Algorithm. IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19（ 6）：580～593.

［4］Goesele M，Curless B，Seitz S M.Multi-View Stereo Revisited［C］. CVPR，New York，NY，2006.

［5］Lourakis M I A，Deriche R.Camera Self-Calibration Using the Kruppa Equations and the SVD of the Fundamental Matrix： The Case of Varying Intrinsic Parameters［R］.INRIA Tech Report，RR-3911，2000.

［6］Sonka M，Hlavac V，Boyle R.Image Processing，Analysis and Machine Vision（2nd Edition）［M］.New York：Thomson Press，2002：460-469.

［7］B.Triggs，P.McLauchlan，R.Hartley，et al.Bundle adjustment- a modern synthesis［J］.Vision algorithms： theory and practice，2000，1883： 298-372.

［8］Y.Furukawa，J.Ponce.Accurate， dense，and robust multiview stereopsis［J］.IEEE Transactions on PatternAnalysis and Machine Intelligen ce，2010，32（8）：1362-1376

林连庆（1985－），女，硕士研究生，现就读于北京航空航天大学计算机学院，研究方向：计算机图形学、图像处理。