超音速弹丸低伸弹道的近似解析解

刘　鹏，王雨时，闻　泉，张志彪

(南京理工大学机械工程学院，江苏 南京　210094)



超音速弹丸低伸弹道的近似解析解

刘鹏，王雨时，闻泉，张志彪

(南京理工大学机械工程学院，江苏 南京210094)

针对引信和弹药试验用超音速弹丸低伸弹道诸元求解过程较为复杂的问题，利用超音速段空气阻力定律有理式函数经验公式求解弹丸低伸弹道质心运动方程组，提出了超音速弹丸低伸弹道诸元中速度与时间的解析函数式。该解析式编程简单，应用方便。实例表明，所得到的超音速弹丸低伸弹道诸元近似解析解公式具有较高的求解精度。

外弹道学；数学模型；经验公式；低伸弹道；外弹道近似解；弹道预估

0　引言

弹药和引信产品研制与生产验收试验以及部队训练试验，涉及的多是低伸弹道问题。虽然计算机及其应用技术已经很普及，但要解算弹丸外弹道，涉及的不但有常微分方程组的数值求解问题，还需要有较为系统的外弹道学知识，而这对非弹道学专业的人员是有一定难度的。

为了寻求便于应用的弹道学解算方法，人们多年来一直在进行探索和研究。这包括计算机普及前诞生的低伸弹道的西亚切近似分析解法(需查西亚切辅助函数表)，也包括计算机普及后的各种近似解析公式。如文献[1]以反坦克火炮为背景，以研究直射程和直射角为主，应用级数展开原理给出了低伸弹道诸元的公式，但计算复杂，应用繁琐；文献[2]利用西亚切阻力定律在初速大于300 m/s情况下的简化表达式，给出了反坦克武器直射距离的计算公式。文献[3]以步兵近战武器弹道为背景，利用低速(小于250 m/s)情况下的平方阻力定律，推导出了低速低伸弹道的任意点诸元求解公式。文献[4]和[5]对此结果作了进一步归纳整理。文献[6]和[7]所用理论和公式与文献[3]的相同。文献[8]以火控计算机为应用背景，针对航炮空中射击弹道，应用最小二乘法将3≥Ma≥1.5的弹丸空气阻力定律曲线处理成了直线，以直接解析法取代传统表解法解算航空炮弹2 000 m以内的外弹道，得出航炮射击诸元。文献[9]利用超高速情况下(大于1 270 m/s)的平方阻力定律，给出了超高速弹丸低伸弹道方程的近似解析解，即速度降与阻力特性之间的关系式。文献[10]借助最小二乘法回归得到的中高速段(400～1400 m/s和630～960 m/s)阻力函数经验公式，给出了中高速段低伸弹道的近似解析解，即飞行时间与速度、飞行距离的解析关系式，但其误差较大。在超出其速度范围之外时，最大相对误差达20%。

本文利用超音速(4≥Ma≥1)弹丸空气阻力定律有理式经验公式，对弹丸低伸弹道近似求解，得到较高精度的弹丸速度和飞行距离解析表达式。

1　对应1943年阻力定律的弹道方程近似解析解

经典外弹道学给出的弹丸质心运动微分方程组[11]为：

(1)

式(1)中，v为弹丸速度，m/s；c为弹道系数，m2/kg；H(y)为空气重度函数，无量纲；F(v,cs)为阻力函数，N/m2；g为重力加速度，m/s2；θ为弹道倾角，(°)；t为发射时记起的时间，s；cs为当地声速，m/s；x为弹丸飞行水平距离，m；y为弹丸飞行高度，m。

对于低伸弹道，可以忽略射角、高度和重力加速度的影响，即θ=θ0≈0，y≈0，H(y)=H(0)=1，从而简化上述的弹丸质心运动微分方程。式(1)中的第一个方程可以简化为：

(2)

对于一个特定的弹丸c是一定的。再将H(y)看作常数，记中间变量p=4.737×10-4cH(y)，p的计量单位为m-1，则式(2)可简化为：

(3)

记马赫数M=v/cs，则式(3)变为：

(4)

代入文献[12]给出的1943年空气阻力定律在1≤M≤4范围内的近似解析函数式

(5)

后作分离变量处理，得

(6)

令q=1/M，则式(6)变为：

即

(7)

利用MATLAB软件解式(7)可得：

11.260q+10.564arctan(2.3330q-3.8846)+

7.2870ln(q2-3.3302q+2.9562)=cspt+A

(8)

式中，A为由初始条件t=0、v=v0(初速)确定的常数。

将q=1/M、M=v/cs代入，得到弹丸速度v与时间t的解析函数式

(9)

该式为超越方程，难以求其反函数，可用数值迭代法求解。

2　数值迭代算法的应用

对于海拔高度为0的低伸弹道而言，H(y)=1，则p=4.737×10-4c。另cs取地面标准值341.2m/s，弹丸初速v0和弹道系数c已知。将q=q初=1/M0=cs/v0=341.2/v0，t=t0=0代入式(8)中即可求得A。

把方程等价变换为：

q=f(q)

只要f(q)在q的值域内连续，且|f′(q)|<1，那么它的根可由：

q1=f(q0)

q2=f(q1)

⋮

qn+1=f(qn)

来接近。令

q=[-10.564arctan(2.3330q-3.8846)-

7.2870ln(q2-3.3302q+2.9562)+

cspt+A]/11.260

(10)

则有

又因为1≤M≤4，则0.25≤q≤1。利用MATALB可求得|f′(q)|在0.25≤q≤1范围内的极值为0.7746<1，则式(10)的迭代过程是收敛的，可以用于外弹道计算。迭代格式为：

qi+1=[-10.564arctan(2.3330qi-3.884 6)-

7.287 0ln(qi2-3.330 2qi+2.956 2)+

cspt+A]/11.260

(11)

对应的v=cs/qn(qn为q的逼近值)。

为了进一步估算出对应的水平位移x，可近似取：

(12)

式中,xt为对应t时刻的水平距离；Δt为时间步长；n=t/Δt；vj为第j个Δt时刻的速度。

3　对应西亚切阻力定律解析式的弹道方程近似解析解

西亚切阻力定律虽已有解析式[11]但却不便于用于弹道方程近似解析解。利用上述方法对文献[12]给出的在1≤M≤4范围内的西亚切阻力定律经验公式

做相同处理。得：

0.016 866lnM+0.016 464/M-

0.455 27ln(M-0.748 79)=cspt+A

(13)

将M=v/cs代入，得到弹丸速度v与时间t的解析函数式为：

0.016 866ln(v/cs)+0.016 464/(v/cs)-

0.455 27ln[(v/cs)-0.748 79]=cspt+A

(14)

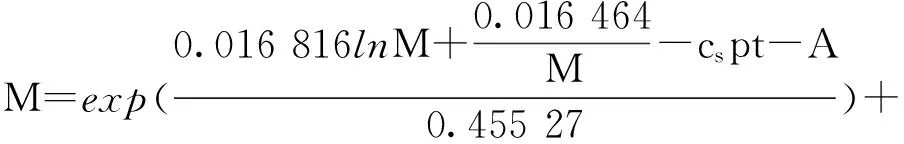
0.748 79,

则

再令式(12)等式左边为：

Φ(M)=0.016 866lnM+0.016 464/M-

0.455 27ln(M-0.748 79)

则

因为1≤M≤4，所以Φ′(M)<0，则Φ(M)在1≤M≤4范围内单调递减，-0.5093≤1≤Φ(M)≤0.6454，对应可知-0.5093≤csat+A≤0.6454。故

利用MATALB软件求得当1≤M≤4时|f′(M)|<0.031<1，则式(13)的迭代过程是收敛的，可以用于外弹道计算。其迭代格式为：

(15)

对应的v=csMn(Mn为M的逼近值)。

与对应1943年阻力定律的弹道方程近似解析解相比，对应西亚切阻力定律的弹道方程近似解析解形式比较简单。

4　验证算例

以25mm口径舰炮榴弹为例，对式(11)和式(12)的准确性进行验证。迭代时取q0=1/M0=cs/v0。查文献[13]知该榴弹初速v0=890m/s、弹重m=0.282kg、弹形系数i43=1.3，计算结果与射表所载[10]数值对比如表1所列。

以23mm口径航炮榴弹为例，对式(15)的准确性进行验证。查文献[13]知该榴弹初速v0=720m/s、弹重m=0.174kg、弹形系数ic=0.66，有效射程不小于1 000m。取射角θ0=1.5°。再利用式(1)对该枪弹进行数值求解，比较结果如表2所列。

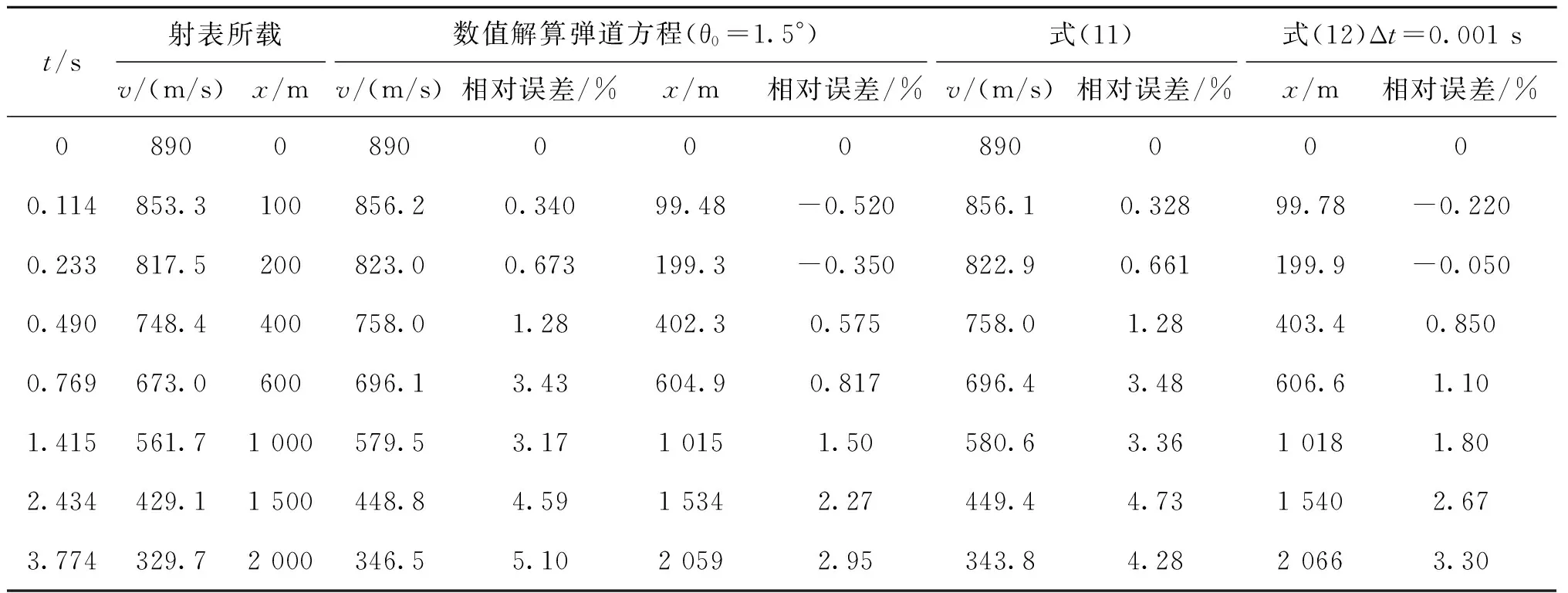
表1　25 mm口径舰炮榴弹外弹道近似解及数值解与射表所载外弹道诸元对比

表2　23 mm航炮榴弹外弹道近似解与数值解对比

由表2可以看出，利用式(12)进行近似解析求解得到的弹丸速度与采用微分方程数值解所得结果差异很小，相对误差在0.103%以内。而在计算弹丸水平位移时，时间步长Δt取值越小，水平距离准确度越高。

由图1可以看出，在超音速范围内时，无论射角大小，弹丸速度近似解析解与数值解相差都很小。在亚音速范围内，速度相对误差随着速度的减小逐渐增大，且射角越大，相对误差越大。4 s以内，式(11)的近似解析解与60°射角时数值解结果最大相对误差为2.61%。12 s以后，式(11)给出的结果出现不稳定现象，其原因是此时已超出了式(11)适用范围(M≥1)。

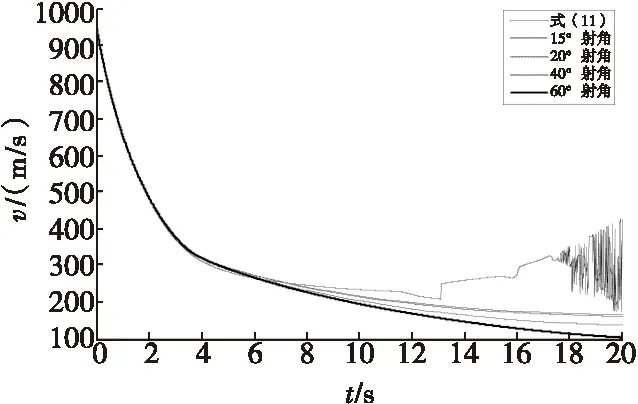
图1　14.5 mm口径四管高射机枪穿燃弹外弹道式(11)近似解析解与不同射角条件下的数值解对比Fig.1　Comparison of four tube 14.5 mm caliber antiaircraft API cartridge ballistic approximate analytical solution of equation (11) and numerical solution under the condition of different jet Angle

由图2可以看出，105 mm坦克炮榴弹的速度近似解析解在超音速段与数值解相差很小，预报弹丸速度的最大相对误差为6.74%。而60 s以后，式(11)给出的结果出现不稳定现象，其原因也是此时已超出了式(11)适用范围(M≥1)。

式(12)的物理意义是计算弹丸的飞行路程。如图3和图4所示，当射角在20°以下时，式(12)的误差较小。而当射角在20°以上时，弹丸的水平位移与路程的差异将随着射角的增大而显著增大，因而式(12)误差较大。

图2　105 mm口径坦克炮榴弹外弹道式(11)近似解析解与不同射角数值解对比Fig.2　Comparison of 105 mm caliber tank gun cartridge ballistic approximate analytical solution of equation (11) and numerical solution under the condition of different jet Angle

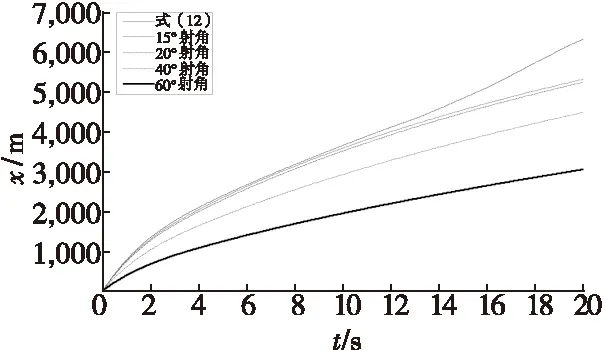
图3　14.5 mm口径四管高射机枪穿燃弹外弹道水平距离近似解与不同射角条件下数值解对比Fig.3　Comparison of four tube 14.5 mm caliber antiaircraft API cartridge ballistic approximate analytical solution of horizontal distance and numerical solution under the condition of different jet Angle

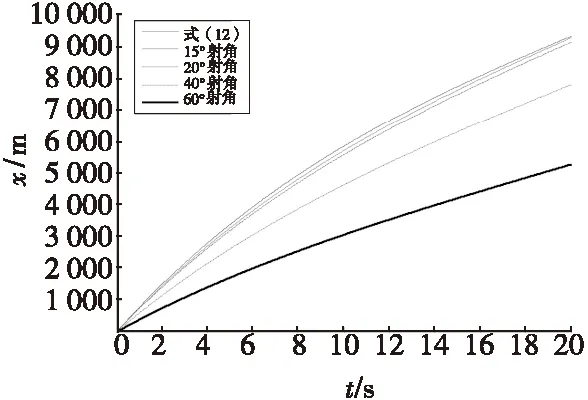
图4　105 mm口径坦克炮榴弹外弹道水平距离近似解与不同射角数值解对比Fig.4　Comparison of 105 mm caliber tank gun cartridge ballistic approximate analytical solution of horizontal distance and numerical solution under the condition of different jet Angle

5　结论

利用弹丸超音速段空气阻力有理式经验公式分析得到的低伸弹道近似解析解，其估算结果与数值解算的结果误差很小。该表达式是低伸弹道的一种数学解法，不需要对外弹道微分方程组进行数值求解，编程简单，应用方便，可用于预估超音速弹丸低伸弹道参数。

[1]杨志远. 火炮直射程和直射角——并导低伸弹道计算公式[J]. 弹箭技术研究，1973(1)：67-84.

[2]林永生.反坦克炮弹外弹道的近似解法[J].弹箭技术研究，1973(1)：85-93.

[3]王连敏. 低速低伸弹道解法[J]. 兵工学报，1981(1)：11-18.

[4]艾西安.枪榴弹[M].北京：国防工业出版社，1986：144-148.

[5]艾西安，孙晓棕，谢乐平，等. 步兵近战武器论证参考[M].北京：国防工业出版社，1986： 96-98.

[6]杨光. 防暴弹低伸弹道实用解法[J]. 武警技术学院学报，1995(2)：38-44.

[7]高义旗，郭三学，周铭，等. 非致命防暴弹外弹道仿真.[J].计算机仿真，2013(8)：10-13.

[8]吴象东. 航空射击弹道的直接解析式求解方法[J].火控技术，1985(1)：35-44.

[9]王雨时, 焦志刚, 于世杰.超速脱壳穿甲弹与阻力特性间的解析关系式[J].山西兵工学报，1994(1)：1-3.

[10]王雨时, 焦志刚, 于世杰. 低伸弹道方程近似解析解[J].山西兵工学报，1994(2)：14-19.

[11]浦发，芮筱亭.外弹道学(修订本)[M].北京：国防工业出版社，1989.

[12]刘鹏，王雨时，闻泉，等. 弹丸阻力定律超音速段有理式经验公式[J]. 弹箭与制导学报，2016(2)：122-124.

[13]侯正礼, 郁作民. 引信手册(第二册)[M]. 北京：兵器工业部三局，1984.

Approximate Analytical Expression of Supersonic Projectile Low Trajectory

LIU Peng, WANG Yushi, WEN Quan, ZHANG Zhibiao

(College of Mechanical Engineering , NUST, Nanjing 210094, China)

For the problem of low trajectory parameters of supersonic projectile for fuze and ammunition test solution was complicated, rational empirical formulas for air resistance law of projectile at supersonic section was uesed to solve mass center motion equations of low trajectory, a analytic function of speed and time of low trajectory for supersonic projectile was present. The analytic function was simple to program and convenient to use. Examples showed that approximate analytic expression of low trajectory for supersonic projectile had higher accuracy.

external ballistics; mathematical model; empirical formula; low trajector; ballistic approximate solution; ballistic forecast

2015-11-03

江苏省自然科学基金青年基金项目资助(BK20140786)

刘鹏(1991—)，男，湖南长沙人，硕士研究生，研究方向：引信及弹药技术。E-mail:skig906@163.com。

TJ012.3

A

1008-1194(2016)04-0042-05