基于失效机理的引信微结构可靠性分析方法

涂宏茂，娄文忠，王辅辅，刘芳怡

(1.中国兵器科学研究院，北京　100089；2.东北大学机械工程与自动化学院，辽宁 沈阳　110819；3. 北京理工大学机电学院，北京　100081)



基于失效机理的引信微结构可靠性分析方法

涂宏茂1,2，娄文忠3，王辅辅3，刘芳怡3

(1.中国兵器科学研究院，北京100089；2.东北大学机械工程与自动化学院，辽宁 沈阳110819；3. 北京理工大学机电学院，北京100081)

针对引信微结构设计分析中仍缺乏有效的可靠性评估方法的问题，结合结构可靠度计算原理，给出基于失效机理的引信微结构可靠性分析方法。该方法以微结构失效模式和失效机理分析为基础，建立表征微结构失效的数学模型，并以此为基础，进行微结构可靠性模型建立，以及可靠度和灵敏度的量化分析。同时，针对可靠度分析程序对CAE软件的调用需求，提出了通用的可靠性分析程序对CAE软件的集成模式，并以ANSYS为例给出了相应的可靠性分析流程。最后，以MEMS安全系统用微弹簧的可靠性分析为例，证明该方法在量化评估微结构可靠性水平方面的可行性和实用性。

引信可靠性；结构可靠度；失效机理分析；失效机理建模；可靠性灵敏度

0　引言

与微电子器件不同，MEMS器件不仅包含电子元件还包含机械元件，并且这些机械元件(如引信用的MEMS悬臂梁、弹簧等，结构特征尺寸在1 μm 至1 mm范围内，后续统称为引信微结构)之间常具有相对的运动或相互的表面作用。在微观尺度下，这些微结构的力学特性发生了很大变化，结构失效模式更多样、失效机理更复杂。例如，在冲击作用下微悬臂梁常发生粘附失效包括S形和弓形两类变形失效形式[1]，采用一般意义上的悬臂梁力学模型难以描述该失效问题。那么，相应的微结构可靠性设计分析需要充分考虑MEMS的特点，更关注结构在微观尺寸下的失效原因和机理，并以此开展可靠性的分析和预计[2]。同时， 由于仿真分析方法能够有

效地预测结构性能，可以在设计早期改进结构设计，其越来越多地应用于引信微结构的设计分析[3-4]。若能在可靠性设计分析中，充分集成已有的仿真分析方法和工具手段，将有助于提高微结构可靠性设计分析的效率，对于预测产品的可靠性并提出具有针对性的改进建议，具有重要作用。

因此，本文以引信微结构为研究对象，从失效机理的层面，给出量化的微结构可靠性分析方法与流程，并以ANSYS为例证明如何结合仿真方法进行可靠性分析。

1　基本问题描述

根据结构可靠度理论，微结构失效概率模型为

(1)

(2)

由式(1)和式(2)可以看出，若已知微结构失效事件(g(x)<0的事件)的统计数据，则可以获取微结构失效的概率，这就是所谓的基于统计的微结构可靠度方法。但是，这一方法的问题在于无法获知微结构失效的原因和规律，无法判别随机变量向量x对微结构的作用情况。如果微结构失效概率预计结果不满足要求，那么基于统计的分析方法难以提出有针对性的改进措施。相反，如果能够进行微结构失效原因和机理的分析，获得微结构的功能函数g(x)表达式，并进行微结构可靠性的分析。那么不仅可以获得微结构失效或安全的概率信息，还可以确定随机变量向量x对结构的影响情况，进而能够给出有效的微结构可靠性设计改进建议。这一方法就是所谓基于失效机理的微结构可靠性分析方法，它的基本流程如图1所示。可以看出，基于失效机理的微结构可靠性分析有两个主要的问题需要解决：一是功能函数g(x)的建立与简化，涉及失效原因和机理分析、失效判据确定等；二是失效概率模型或可靠度模型的求解，包括失效概率或可靠度的计算和可靠性灵敏度的分析等。

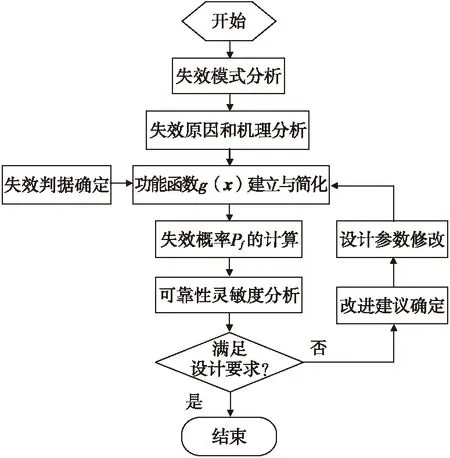
图1　基于失效机理的微结构可靠性分析流程Fig.1　Reliability analysis procedure of micro-structure based on failure mechanism

2　失效机理分析与建模

2.1引信微结构失效机理分析

在MEMS引信系统设计分析中，常用的微结构包括微型弹簧、微型悬臂梁(包括一端固定和两端固定两种)、微型铰链、微型齿轮、微型反射层，以及其他一些微型薄板、壳结构等[5-6]。这些结构的失效模式与机理与相应的宏观结构差别比较大，结合文献[2]和文献[7]，可以归纳出其常见的失效模式与机理，如表1所示。

表1　微结构常见失效模式与机理

在微结构失效机理分析方面，国内外很多专家学者主要从外部载荷、材料特性等方面入手，做了很多的研究工作。如Walraven[8]依据MEMS结构不同的作用特点(是否具有相对运动、是否相互摩擦或冲击等)进行了分类，并针对每种类型给出了失效原因和机理的分析。Tanner等人[9]分析振动、冲击和湿度环境对微机械系统的影响，结合试验结果确定主要的失效模式与失效机理；Shea[10]分析了真空、辐射、温度冲击环境下的MEMS结构失效机理，给出相应的可靠性改进措施；Pomeroy等人[11]采用光谱分析设备开展了MEMS结构动态应力测试方法研究，并基于此进行可靠性的分析；Jadaan等人[12]基于威布尔分布研究MEMS脆性材料性质，并用于预测材料在寿命期内的行为特性。

总的来说，在进行微结构失效机理分析时，一方面常采用试验方法进行MEMS材料特性、微结构应力或应变响应等的测定，另一方面常借助仿真方法进行微结构运动学、动力学特性的分析，或者采用二者相结合的方法，确定影响微结构性能和可靠性的主要因素。

2.2引信微结构失效机理建模

为了进行微结构的量化可靠性分析，需要在失效机理分析的基础上，结合失效判据，建立相应的数学模型，为后续的可靠性分析提供输入。在结构可靠性分析中，常采用如式(1)所示功能函数g(x)表征结构失效，因此，失效机理的建模的目的就是获得功能函数的表达式。

功能函数g(x)可以改写为：

g(x)=S(x)-s(x)

(3)

式(3)中，S(x)为广义强度，可以是微结构材料强度、允许最大变形量、允许最大应力值等；s(x)为广义应力，可以是微结构应力响应、应变响应等；二者都可以是随机变量向量x的函数。

由式(3)可以看出，功能函数g(x)可以是显式的解析表达式，也可能是隐式函数，尤其当s(x)是通过有限元程序等获得的应力或应变响应时，g(x)将为具有较强非线性的隐式函数，这将会增加后续可靠性分析的复杂程度。尤其是在单次有限元计算时间较长的情况下，相应的可靠性分析成本将急剧增加。为解决这一问题，可以采用近似模型替代s(x)，从而使功能函数g(x)显式化，便于后续的可靠性分析。近似模型又称为响应面模型，是在获得多组输入变量向量x和对应输出s(x)的样本数据的情况下，采用简单函数近似表征输入输出样本点数据关系。一般情况下，s(x)近似模型可以写为：

s(x)=fT(x)b+ε

(4)式(4)中，fT(x)=(f1(x),…,fp(x))T，fi(x)通常为选定的多项式函数，i=1,…,p；b=(b1,…,bp)T为相应的待定参数，在已知多组样本数据情况下，可以采用最小二乘法等确定这些参数值；ε为随机误差。

常用的近似模型建立方法有曲线拟合法和插值法两类，其中曲线拟合法包括最小二乘法、正交多项式法等，插值法包括Kriging法、Lagrange插值法、样条插值法等。不难看出，为建立近似模型的需要获取输入输出样本数据，这就需要进行多组输入x样本数据下对应的输出s(x)计算，若采用有限元法获取应力或应变响应，则仍需要多次调用有限元程序进行计算。但是，相对于不采用近似模型的可靠性分析来说，这已大大降低了有限元调用次数，同时，显式化的功能函数也将有效降低梯度计算的难度，便于采用一次二阶矩法等进行快速的可靠性分析。

3　引信微结构可靠性分析

引信微结构可靠性分析的目的，一是获得结构可靠度，用于评价结构设计是否满足指标要求；二是结构可靠性灵敏度分析，用于确定影响结构可靠性的主要因素。下面结合引信微结构的特点和结构可靠性分析理论，介绍引信微结构可靠度计算和灵敏度分析的基本方法。

3.1结构可靠度计算原理

依据概率理论，假设随机变量向量x的联合概率密度函数为fx(x)，式(1)所示的概率模型可转化为如式(5)所示的积分形式：

(5)

可以看出，结构失效概率和结构可靠度分别等于fx(x)在失效域g(x)<0和安全域g(x)>0内的积分。可以采用蒙特卡洛法或有关的改进方法(重要抽样法等)进行式(5)的计算，即通过抽样计算，统计落入失效域的样本数量，进而得到失效概率或可靠度。但该方法的计算次数相对较多，更多的工程应用则采用FORM(First Order Reliability Methods, 包括一次二阶矩法及其改进方法)和SORM(Second Order Reliability Methods, 包括二次二阶矩法及其改进方法)。

在实际应用中，采用FORM或SORM进行失效概率或可靠度计算时，常常需要解决两方面的问题：一是确定多个随机变量的联合概率密度函数；二是降低积分边界g(x)=0的非线性程度。针对第一个问题，可以将随机变量向量由原始空间(X-空间)转换至标准正态空间(U-空间)[13]，相应的式(5)可以修改为：

(6)

式(6)中，G(u)和φu(u)分别为功能函数g(x)和概率密度函数fx(x)在U-空间的表达式，其中φu(u)为标准正态分布概率密度函数。关于X-空间、U-空间的定义，以及有关的转换关系可以参考文献[13]。针对第二个问题，通过基于MPP(Most Probable Point，最可能失效点)泰勒展开方法，将功能函数转化为线性函数或二次函数，式(7)给出了FORM中线性化的功能函数表达式

G(u)≈G(u*)+G(u*)(u-u*)T

(7)

式(7)中，u*为U-空间中的MPP；G(u*)为G(u)在MPP处的梯度。

图2、图3分别给出了两个随机变量情况下，X-空间的概率积分，以及U-空间内基于FORM的概率积分的示意图。

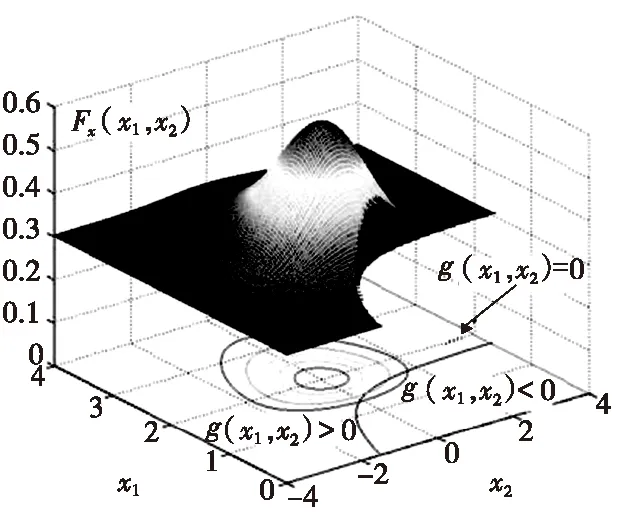
图2　X-空间概率积分示意图Fig.2　Probability integration in X-space

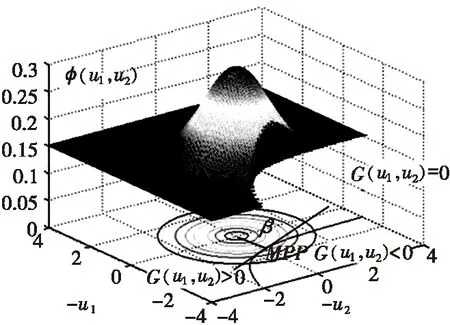
图3　基于FORM的概率积分示意图Fig.3　Probability integration based on FORM in U-space

对比图2和图3可以看出，概率密度函数转换至U-空间后，它的等高线为一组同心圆，这是概率密度函数“规则化”的体现，这将简化积分运算。同时，可以证明图2中的同心圆圆心至MPP的距离β等于Φ-1(R)[13-14]，即有

(8)

β又称为可靠度指数，它与可靠度直接的对应关系。关于FORM、SORM，以及有关的改进方法的基本原理和计算流程可以参考文献[13]、文献[14]，或有关的标准，这里不再赘述。

3.2基于CAE的可靠度计算方法

在引信微结构的分析中，常采用CAE工具(如ANSYS、COMSOL Multiphysics等)进行应力、应变分析，为确定可靠性薄弱环节提供依据。同时，在可靠度计算中将需要多次调用CAE工具，评估不同输入情况下的性能响应。因此，有必要在可靠性分析程序中实现对CAE工具的集成，满足可靠性分析中对CAE的多次调用需求。

在可靠性分析中集成CAE工具需要着重解决三个问题：一是修改CAE输入文件的变量值；二是以批处理方式(Batch Mode)调用CAE进行求解；三是获取CAE计算结果。图4给出了通用的可靠性分析程序与CAE集成模式，其中，可靠性分析主程序需要读入CAE输入文件，并修改有关的变量值，获得更新后的输入文件；用批处理命令调用CAE工具进行求解，并监测求解状态；在求解完毕后，读入CAE结果文件，获取求解结果。

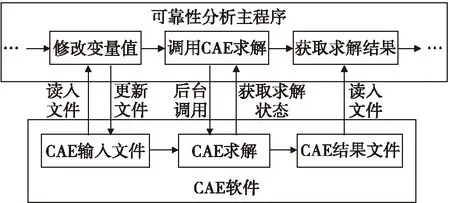
图4　通用的可靠性分析程序与CAE集成模式Fig.4　General CAE integration mode for reliability analysis procedure

下面以ANSYS为例给出了基于CAE的FORM计算流程，如图5所示。其中，u*初始值一般对应于X-空间的均值点。关于ANSYS的输入输出文件格式，以及调用命令等内容，可以参考ANSYS的帮助文档。

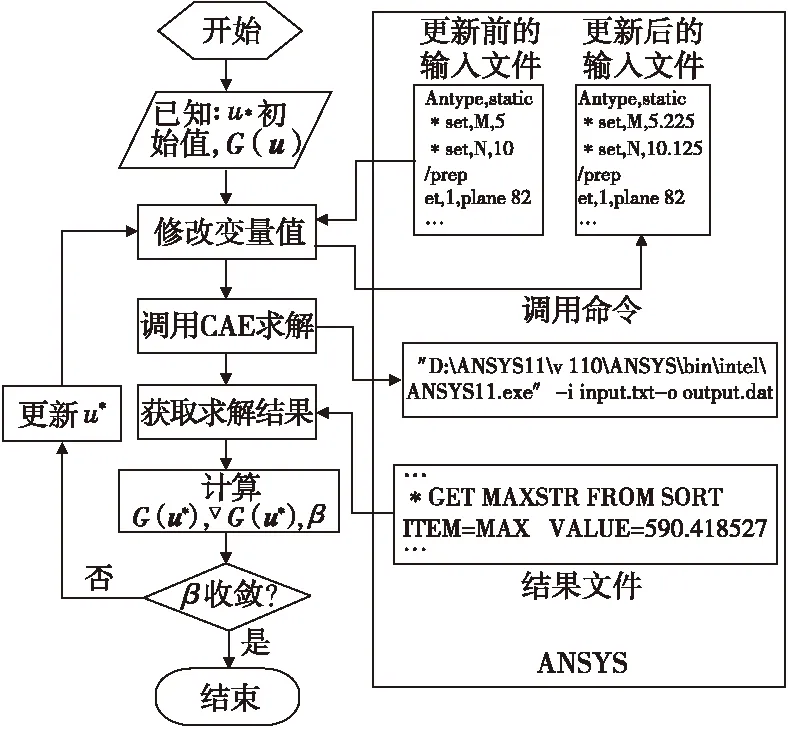
图5　基于CAE的FORM计算流程Fig.5　FORM procedure based on CAE

3.3可靠性灵敏度分析方法

可靠性灵敏度分析主要用于对各随机变量重要性程度的横向对比。在U-空间内，重要性灵敏度定义为：

(9)

式(9)中，L为随机变量相关系数矩阵经过Cholesky分解后的下三角矩阵。在X-空间内，重要性灵敏度为：

(10)式(10)中，σi为第i个随机变量的标准差或等效标准差(非正态分布的情况)，i=1,…,n，有n个随机变量；diag(σi)是n×n矩阵，对角线的元素为σi，其他元素为0。

式(9)和式(10)只是可靠性灵敏度在不同变量空间的表达式，二者本质上是一样的。同时，可以看出，可靠性灵敏度不仅考虑了随机变量之间的相关性，还可以考虑了随机变量的离散性，因此，它区别于确定性意义上的灵敏度，又称为概率灵敏度。

在实际应用中，如果采用FORM或SORM方法进行可靠度计算，那么可靠性灵敏度可以直接获得；如果采用蒙特卡罗及有关的改进方法，那么需要进行数据样本的处理，才可以获得灵敏度信息，具体的可以参考文献[15]。另外，如果要获得失效概率或可靠度关于随机变量的灵敏度，则可以通过可靠度/失效概率与可靠度指数的函数关系，利用复合函数求导获得。

4　示例

MEMS安全系统如图6(a)所示，其核心的MEMS器件(平面W型微弹簧)结构如图6(b)所示，弹簧节数n=8，厚度w=150 μm，使用UV-LIGA工艺制备，材料为Ni。在外部冲击载荷下，弹簧易出现断裂失效问题，针对这一问题，考虑各类随机因素的影响，进行相应的可靠性分析。取冲击载荷峰值为F=40 mN，持续时间12 ms，材料屈服强度为σ=1.05 GPa，弹性模量E=210 GPa泊松比υ=0.31，涉及的随机变量分布类型及其参数如表2所示。

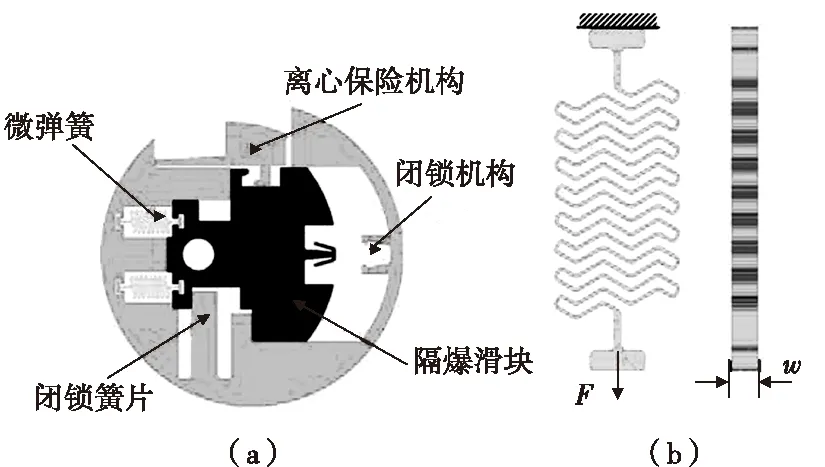
图6　MEMS安全系统用平面W型微弹簧示意图Fig.6　Schematic diagram of plane W micro-spring

变量分布类型均值标准差w/μm正态分布15015F/mN正态分布404σ/GPa正态分布1.050.12

1)失效机理机理分析与建模

微弹簧在冲击载荷作用下发生断裂破坏，失效的主要原因是最大冲击应力大于材料屈服极限。因此，可以获得表征微弹簧失效的功能函数

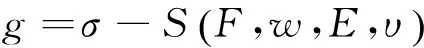
(11)

式(11)中，S(F,w,E,υ)为微弹簧在冲击载荷作用下的最大响应应力，此处取为节点Von Mises应力,它是利用ANSYS计算得到的；泊松比υ为常数。

2)可靠性建模

由式(10)可知，当g>0时，微弹簧是安全的；当g<0，微弹簧是危险的；极限状态为g=0。微弹簧的可靠度为g>0的概率，对应的可靠度模型为：

(12)

3)可靠性分析

依据图4所示的方法集成ANSYS，进行式(12)的求解，可以获得微弹簧的可靠度R=0.972 5 (可靠度指数β=1.919 5)，迭代次数为7次,有限元计算次数为29次，计算时间约为31 min。灵敏度结果如图7所示。

可以看出，材料屈服强度σ和厚度w与微弹簧的可靠度指数呈正比，而载荷F则与之呈反比；σ的影响比尺寸w和F都大些。

另外，需要指出的是，由于本算例调用ANSYS进行有限元计算，且单次计算耗时约为1min，故无法采用Monte-Carlo直接进行结果的验证(若抽样次数为105次，则需要耗时约105min)。因此，在实际计算中，主要从以下两方面来保证算例的计算精度：一是通过不含有限元计算的解析算例验证可靠度灵敏度计算方法的正确性，另一方面是通过试算确保ANSYS调用接口和调用流程的正确性。

5　结论

本文结合结构可靠度计算原理，给出了基于失效机理的引信微结构可靠度和灵敏度计算方法。该方法在微结构失效模式和失效机理分析的基础上，建立表征微结构失效的数学模型，进而开展微结构可靠性模型建立，以及可靠度和灵敏度的量化分析。结合可靠度分析程序对CAE软件调用的实际需求，提出了通用的可靠性分析程序与CAE集成的基本模式，以ANSYS为例给出了基于CAE的一次可靠度(FORM)计算流程。对MEMS安全系统用微弹簧开展可靠性分析，结果表明，该方法能够给出量化的可靠度与灵敏度信息，在量化评估微结构可靠性水平方面具有可行性和实用性。

[1]王佩瑶, 唐洁影, 余存江, 等.MEMS微悬臂梁在冲击下的粘附失效预测[J]. 传感技术学报, 2006, 19(5): 1602-1605.

[2]WMerlijnvanSpengen.MEMSreliabilityfromafailuremechanismsperspective[J].MicroelectronicsReliability, 2003(43): 1049-1060.

[3]景华, 牛兰杰, 宋永强. 小口径榴弹引信微机电安全系统设计与仿真方法[J]. 弹箭与制导学报, 2010, 30(2): 129-132.

[4]程玄玄, 聂伟荣, 李艳桥，等. 引信MEMS保险机构剪断式后坐卡销[J]. 弹箭与制导学报, 2011, 31(6): 102-104.

[5]LafontanX,PressecqF,BeasdoinF,etal.TheadventofMEMSinspace[J].MicroelectronicsReliability, 2003(43):1061-1083.

[6]MarcelWPruessner,ToddTKing,DanielPKelly,etal.MechanicalpropertymeasurementofInP-basedMEMSforopticalcommunications[J].SensorandActuatorsA, 2003(5): 190-200.

[7]BhushanB.SpringerHandbookofNanotechnology[M].NewYork：Springer, 2007.

[8]WalravenJ.FuturechallengesforMEMSfailureanalysis[C]//ProceedingsInternationalTestConference(ITC’03).US:LTC, 2003： 850-855.

[9]TannerD,WalravenJ,IrwinM，etal.Theeffectofhumidityonthereliabilityofasurfacemicromachinedmicroengine[J].Proceedingsofthe37thAnnualIEEEInternationalReliabilityPhysicsSymposium(IRPS’99).SanDiego,Cailf,USA, 1999: 189-197.

[10]SheaH.ReliabilityofMEMSforspaceapplications[J].ProceedingsoftheSPIE, 2006：305-311.

[11]PomeroyJ,GkotsisP,ZhuM,etal.DynamicoperationalstressmeasurementofMEMSusingtime-resolvedRamanspectroscopy[J].JournalofMicroelectromechanicalSystems, 2008, 17(6): 1315-1321.

[12]JadaanO,NemethN,BagdahnJ,etal.ProbabilisticWeibullbehaviorandmechanicalpropertiesofMEMSbrittlematerials[J].JournalofMaterialsscience, 2003, 38(20): 4087-4113.

[13]秦权, 林道锦, 梅刚. 结构可靠度随机有限元-理论及工程应用[M]. 北京：清华大学出版社, 2006： 161-178.

[14]李良巧.机械可靠性设计与分析[M].北京：国防工业出版社，1998.

[15]WuYT,MohantyS.Variablescreeningandrankingusingsampling-basedsensitivitymeasures[J].ReliabilityEngineeringandSystemSafety, 2006, 91(6): 634-647.

Fuze Micro-structure Reliability Analysis Based on Failure Mechanism

TU Hongmao1,2, LOU Wenzhong3, WANG Fufu3, LIU Fangyi3

(1. Ordnance Science and Research Academy of China, Beijing 100089, China；2. College of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China；3. School of Mechanical-electronic Engineering, Beijing Institute of Technology, Beijing 100081, China)

In order to quantitatively evaluate the reliability of the fuze micro-structure in design stage, a reliability analysis method based on the structural reliability calculation principles and the failure mechanisms was proposed. in this paper. Based on this model, reliability model was obtained and used for further reliability and sensitivity calculations. To facilitate the use of CAE software in the reliability program, which gave the general CAE integration mode for structural reliability analysis. The detail procedure of the structural reliability analysis based on ANSYS was depicted. A reliability analysis example of micro-spring in fuze safety mechanism demonstrated the feasibility and practicality of the method for fuze micro-structure reliability problems.

fuze reliability; structural reliability; failure mechanism analysis; modeling; probabilistic sensitivity

2016-02-25

国防技术基础项目(Z092014B001)

涂宏茂(1981—)，男，福建泉州人，博士研究生，副研究员，研究方向：MEMS可靠性。E-mail:bjthm@126.com。

TB114.3

A

1008-1194(2016)04-0009-06