一种全自动相机标定系统的设计

王逊扬, 金　锋

(1. 沈阳大学 信息工程学院, 辽宁 沈阳　110044;2. 北京经纬信息技术公司, 北京　100081)



一种全自动相机标定系统的设计

王逊扬1,2, 金锋1

(1. 沈阳大学 信息工程学院, 辽宁 沈阳110044;2. 北京经纬信息技术公司, 北京100081)

提出了一种基于最小凸包理论的棋盘格角点自动提取算法,结合张正友的经典标定模型,设计一种全自动相机标定系统.实验表明,该系统在复杂的光照和背景条件下,具有很好的标定精度和可靠性.

相机标定; 凸包理论; 角点提取; 自动标定

相机标定作为视觉测量的首要任务,标定结果的准确性和可靠性对后续的研究工作起到至关重要的作用.目前,应用比较广泛的相机标定方法包括了三种类型:传统相机标定方法、相机自标定方法和基于主动视觉系统的标定方法[1].传统标定方法具有鲁棒性和精度高的优点,其中,以张正友提出的柔性桌面标定法[2]为典型代表.张正友标定算法精度适中、计算量小且操作简单、灵活而得到广泛的推崇.Bouguet等人设计了一种MATLAB标定工具箱方法[3],利用张正友的算法进行参数的计算,但该工具箱的自动化程度不高,需要人工界定标定板的顶点,而且需要对多幅图像进行处理,导致整个标定过程十分耗时.本文提出了一种新的基于最小凸包理论的棋盘格特征点自动提取算法,利用张正友标定模型进行参数的自动计算,并以文本形式输出,操作简单高效,且标定精度与MATLAB标定工具箱结果相当.

1　张正友标定模型

1.1相机参数的初始估计

假定将模板平面放置在世界坐标系Z=0的平面上,则相机成像模型为:

(1)

式中,(u,v)为像素坐标系一点,(X,Y,Z)空间三维点.

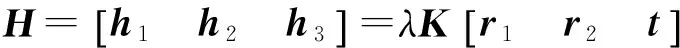
(2)

由于内参矩阵中包含5个未知参数,故当拍摄的图像数目大于等于3时,就可以线性唯一求解出内参.令

(3)

(4)

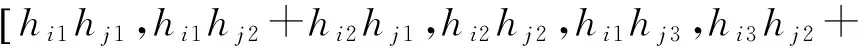
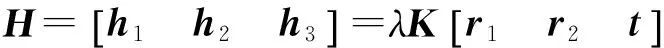
理想状况下,像素坐标与空间点坐标通过相机参数投影在像素坐标系中的点是同一个点,但实际情况会有偏差,为了使相机参数更加精准,利用下面的投影误差最小化函数[4]迭代求精.

(5)

式中,m表示像素坐标系下的坐标,m(K,Ri,ti,Mj)表示空间M点经过初始估计的相机参数投影到像素坐标系下的坐标.

2　棋盘格网格交点特征提取

2.1棋盘格四极点的自动识别

棋盘格的四极点就是棋盘格四个顶角处的角点.棋盘格四极点的识别对于角点的排序起到至关重要的作用.

(1) 最小凸包定义.最小凸包:包含一个平面有限点集S的最小凸区域(区域内任意两点的连线总在区域内)称为S的最小凸包.由定义可知,最小凸包包含S中所有的点,且凸包顶点必属于S,凸包的面积应是包含点集S区域中最小的一个[5].由全部点得到有限点集S,而线段组成的凸多边形即点集S最小凸包.

(2) 求取最小凸包.①起始点确定.确定最小凸包时,必须找到最小凸包内其中一点定义成计算过程起始点.这一点的选择往往以横坐标、纵坐标极值点进行处理,本文将纵坐标最小点定义成起始点,记为P0.②顶点排序.如果点集中最小凸包具备N (N≥3)个顶点,以P0作为起点结合一定规律进行排序,最终辨认出最小凸包剩下(N -1)个顶点数量,同时标注成(P1,P2,…,PN-1).本文中的顶点排序规律为:将P0点和其余点进行连接,得出ov轴至其他连线逆时针转角,把最小转角θ1min对应的点标记为P1;接着让P1点和其他点进行连接,得出P0P1至其他连线逆时针转角,把最小转角θ2min对应的点标记为P2;按照这样的规侓,第k (2≤k≤N)个顶点Pk能够符合Pk-2Pk-1和Pk-1Pk逆时针转角θkmin最小的规律;该过程反复循环,直到通过θNmin得到的定点和起点P0重合,图1为该过程的结果图.

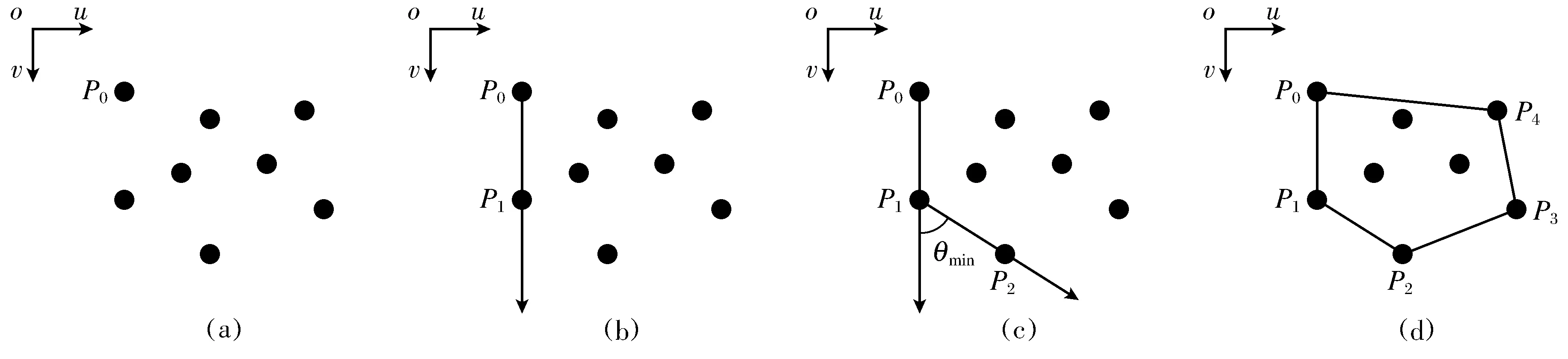
图1　最小凸包生成过程Fig.1　Generation processing of the minimum convex hull

(3) 求棋盘格四极点.如图2所示,通过最小凸包算法可以得到图像角点集中最小凸包数据,利用这种模式能够准确获得棋盘格中最小凸包顶点,同时棋盘格最小凸包内四个顶点即为对应的四极点.

图2　最小凸包序列形成Fig.2　The sequence of minimum convex hull

棋盘格图像角点集最小凸包的获取是棋盘格四极点可以有效识别的关键.以下模式中结合棋盘格四极点相关特征可以完成对它的最终识别.一般而言,棋盘格最小凸包内四个顶点即为对应的四极点.一般情况下,角点集中两个角点的直线距离最大的两组角点就是棋盘格四极点.棋盘格角点集最小凸包顶点为(P0,P1,…,Pk,…,PN-1),将每个顶点与其他顶点相连,计算出两两顶点间的直线距离,进行比较得出距离最大的两组顶点(四个顶点)即为候选极点,记作(A,B,C,D).结果图3所示.

图3　棋盘格四极点Fig.3　Four poles of checkerboard

2.2角点自动排序

通过棋盘四极格点对矩阵H进行处理,利用单应性矩阵可以将角点对应空间坐标变换为角点图像坐标,这一模式可以实现角点在空间坐标系和图像坐标系的相互转变,对角点进行排序.

(1) 单应性矩阵H的计算.棋盘格角点图像像素坐标(u,v)和空间坐标(Xw,Yw)两者符合一定的变换联系:

(6)

变换矩阵H又可以称作单应性矩阵,确定h33=1,H中存在8个未知参数.因事先得到了棋盘格角点空间坐标,如果计算出单应性矩阵H,则能够获得棋盘格所有角点图像像素坐标,图像点、空间点两者也将能够得到有效匹配.很显然,若想使棋盘格角点得到有效的排序,必须尽快获得单应性矩阵H.由于单应性矩阵H中存在8个未知数,则必须通过4个角点对应的图像与空间坐标方可得到H.如果摄像机不存在畸变,已知棋盘格内部任意4个角点坐标均能获得H;但摄像机是存在畸变的,利用棋盘格的四极点计算所得单应性矩阵H就更适合于整幅棋盘格图像.

将已求出的四个极点坐标的的空间坐标设为(0,0)、(0,1)、(1,1)、(1,0),而四个极点坐标已知(u1,v1)、(u2,v2)、(u3,v3)、(u4,v4),则上式变化为:

(7)

H即求出.

(2) 角点排序.开始阶段设置棋盘格行列两方向上的的角点数量为mr与mc,因上一操作中确定两极点空间距离是1,由此可得行方向上角点间的空间距离为1/(mr-1),列方向上角点间的空间距离为1/(mc-1)(实际中通常把棋盘格设为正方形,即有1/(mr-1)=1/(mc-1)).棋盘格各角点的空间坐标可如下计算:

(8)

其中i=(0,1,…,mr-1),j=(0,1,…,mc-1)分别为各角点在棋盘格中的行列号.

将H和(Xiw,Yjw,1)代入式(6),获取相关图像坐标(ui,vi),至此,形成角点图像坐标(ui,vi)和空间坐标(Xiw,Yjw,1)两者的对应关系,最终实现角点排序.

2.3角点的精确定位

为了完成相机的精确标定,必须将角点定位到亚像素级.故此,把像素级角点坐标(ui,vi)确定成初始点,为方便起见,利用灰度梯度法[6].如图4所示,在邻域内的角点,可分为两类.在边缘处点Pk与非边缘处点Pj,Q点代表着亚像素级角点所处位置.Pk灰度梯度方位与QPk垂直,由于Pj灰度梯度为0,那么Q点邻域内的点P其灰度梯度全部和QP垂直,即

(9)

式中,Pi为Q邻域内的任意一点,为Pi点的灰度梯度向量.因现实中的图像受到噪音等条件的干扰,式(9)通常不等于0,加入误差值εi进行处理,则存在式(10):

(10)

以像素级角点为中心取一窗口,计算误差和

(11)

可以通过计算S最小的点的方式获得亚像素Q点位置.将像素级角点Q0作为初始值,完成迭代优化,便能够获取准确的亚像素角点Q.

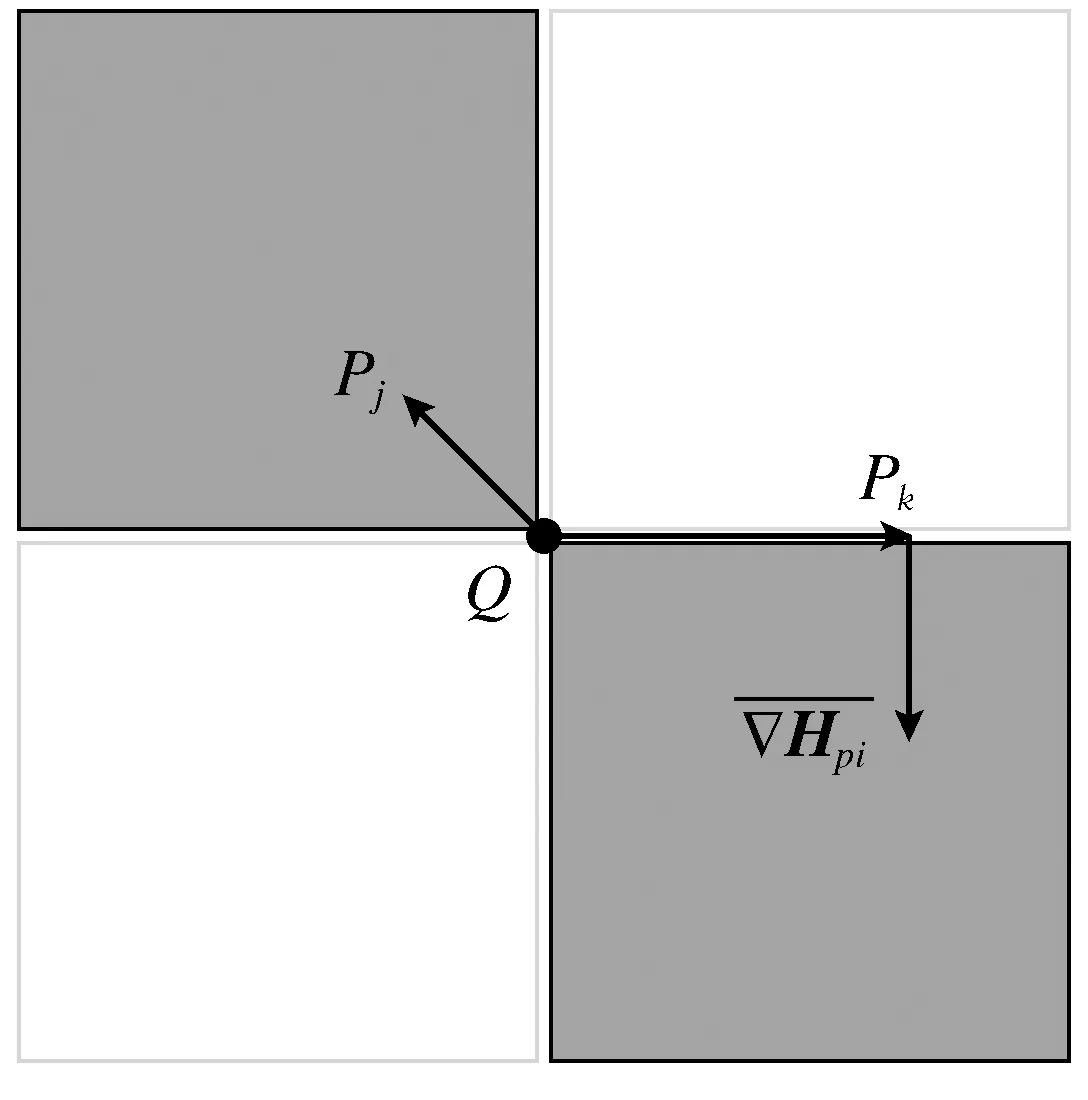
图4　棋盘格角点与灰度梯度Fig.4　Checkerboard corners and gray gradient

3　实验与结果分析

实验采用Basler工业相机,计算机配置为AMD FX-6300处理器,主频3.5 GHz,内存8GB,操作系统为Windows 8.1 64位专业版.按照文献[3]中建议,选择位置和角度适中,在光线较暗、背景复杂的环境下拍摄的12幅图像作为标定图像,如图5所示,图像分辨率为640×480.利用Microsoft Visual Studio 2010软件,在VC++ 2010和OpenCV2.4.8环境下编写了标定工具箱软件,将本文的的角点提取算法结合张正友经典标定法编入进行系统实现,与文献[3]中的Matlab标定工具箱方法的结果进行对比,结果对比见表1.

图5　标定图像Fig.5　The images used as calibration 表1　实验结果对比表 Table 1　Correlation table of experimental results

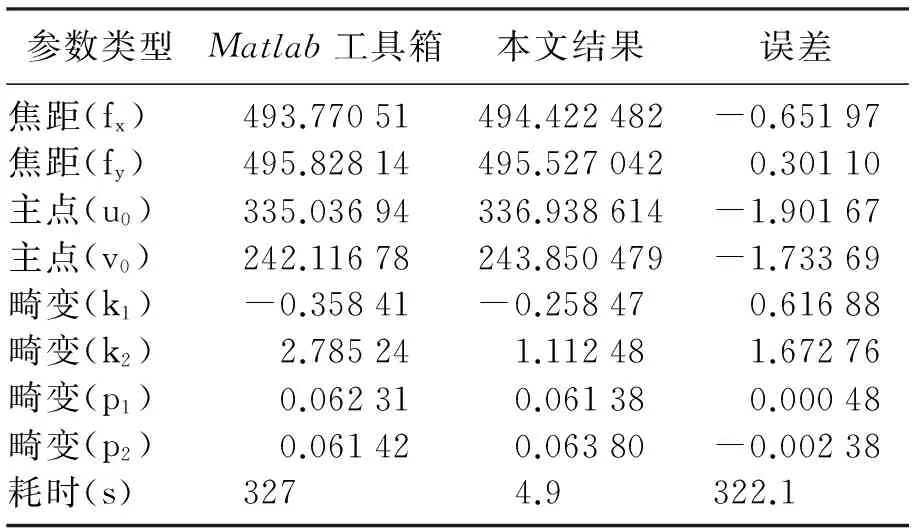
参数类型Matlab工具箱本文结果误差焦距(fx)493.77051494.422482-0.65197焦距(fy)495.82814495.5270420.30110主点(u0)335.03694336.938614-1.90167主点(v0)242.11678243.850479-1.73369畸变(k1)-0.35841-0.258470.61688畸变(k2)2.785241.112481.67276畸变(p1)0.062310.061380.00048畸变(p2)0.061420.06380-0.00238耗时(s)3274.9322.1

结合表1不难发现,通过本文的方法所得标定结果和Matlab工具箱获取的结果精度相当,但是本文的方法耗时明显小于Matlab工具箱,大大提高了标定效率.实验证明,本文方法适用范围很广, 图6在光线较暗、背景复杂的环境下,应用本文的方法,均能快速准确的检测棋盘格角点.

图6　复杂环境下的角点提取结果Fig.6　The results of corners extraction under complex environment

4　结　　论

本文以棋盘格角点提取为切入点,与张正友的标定算法相结合,最终实现了相机的全自动标定.实验结果显示了本文所设计的标定系统在不同场景和光照条件下,同样能自动、准确和快速的完成实验.本系统除了在标定前输入棋盘格数和尺寸,整个标定过程无需人工干预,自动显示标定结果,并按照标准格式导出,适合各个层次的计算机视觉研究者.

[1] 邱茂林,马颂德,李毅. 计算机视觉中摄像机定标综述[J]. 自动化学报, 2000,26(1):43-55.

(QIU M L ,MA S D,LI Y. Overview of camera calibration for computer vision[J]. Acta Automatica Sinica, 2000,26(1):43-55.)

[2] ZHANGZ Y. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000,22(11):1330-1334.

[3] BOUGUET J Y. Camera calibration toolbox for MATLAB[J]. High Speed Vision System & Object Tracking, 2010.

[4] STRICKLAND R N,CHANDLER D W. Reconstruction of an axisymmetric image from its blurred and noisy projection[J]. Applied Optics, 1991,30(14):2585-2588.

[5] 刘人午,杨德宏,李燕,等. 一种改进的最小凸包生成算法[J]. 大地测量与地球动力学, 2011,31(3):130-133.

(LIU R W,YANG D H,LI Y,et al. An improved algorithm for producing minimum convex hull[J]. Journal of Geodesy and Geodynamics, 2011,31(3):130-133.)

[6] 刘涛,陈国柱,李元宗. 亚像素角点定位提高相机标定精度[J]. 机械工程与自动化, 2007(4):28-30.

(LIU T,CHEN G D,LI Y Z. Using subpixel corner detection to improve calibration precision[J]. Mechanical Engineering & Automation, 2007(4):28-30.)

【责任编辑: 肖景魁】

Design of Fully Automatic Camera Calibration System

WangXunyang1,2,JinFeng1

(1. College of Information Engineering, Shenyang University, Shenyang 110044, China; 2. Beijng Jingwei Information Technology Corporation, Beijng 100081, China)

An automatic corners extraction calibration method, combined with Zhang’s classic calibration algorithm, is proposed based on minimum convex hull theory. A fully automatic camera calibration system is designed. Experimental results show that the method has a good calibration accuracy and reliability under the complex lighting and background conditions.

camera calibration; convex hull theory; corners extraction; automatic calibration

2015-12-03

王逊扬(1989-),男,辽宁沈阳人,沈阳大学硕士研究生.

2095-5456(2016)04-0311-04

TP 391

A