Uniform Blow-up Behavior for Degenerate and Singular Parabolic Equations

LIU Bing-chen，ZHANG Chang-cheng

（College of Science，China University of Petroleum，Qingdao 266580，China）



Uniform Blow-up Behavior for Degenerate and Singular Parabolic Equations

LIU Bing-chen，ZHANG Chang-cheng

（College of Science，China University of Petroleum，Qingdao 266580，China）

This paper deals with the degenerate and singular parabolic equations coupled via nonlinear nonlocal reactions，subject to zero-Dirichlet boundary conditions.After giving the existence and uniqueness of local classical nonnegative solutions，we show critical blowup exponents for the solutions of the system.Moreover，uniform blow-up behaviors near the blow-up time are obtained for simultaneous blow-up solutions，divided into four subcases.

egenerate and singular parabolic equations；critical blow-up exponents；uniform blow-up behavior

2000 MR Subject Classification：35K67，35K65，35K61，35B33，35B40

Article ID：1002—0462（2016）02—0125—14

Chin.Quart.J.of Math.

2016，31（2）：125—138

§1.Introduction

In the paper，we study the degenerate and singular parabolic equations coupled via nonlinear nonlocal sources，taken of the formswhere constants a，m，n，p，q，pi，qi＞0（i=1,2），α,β∈［0,2）；u0（x）,v0（x）∈C2+γ（［0,a］）with some constant γ∈（0,1）are nonnegative and nontrivial，satisfying the compatibility conditions on the boundary；T denotes the maximal existence time of system（1.1）.The parabolic equations in system（1.1）are degenerate and singular，since the coefficients of ux，uxxand vx，vxxmay tend to 0 or∞as x tends to 0，which describe the conduction of heat related to the geometric shape of a body（see［1］and references cited there）.

For the scalar problem of（1.1），Chen，Liu and Xie［2］studied the following problem

and obtained the uniqueness and existence of local classical solutions.Under some conditions，the global existence and blow-up criteria of the solutions are discussed.Moreover，the blowup sets are almost the whole［0,a］.For the coupled problem of（1.2），Peng，Yang and Xie［3］considered the following nonlinear parabolic system

where α,β∈［0,2）.Firstly，they obtained the uniqueness and existence of classical nonnegative solutions.Secondly，they proved that，if m＜1，p＜1，nq≤（1-m）（1-p）and α,β∈［0,2），then all solutions remain global.On the contrary，if one of the conditions m＞1，p＞1，nq＞（1-m）（1-p）holds，then the solutions blow up for sufficiently large initial data and remain global for sufficiently small initial data.They also proved the blow-up set and uniform blow-up rates.

Recently，Zhou and Mu［4］considered the parabolic equations，involving moving sources，

where α,β∈［0,2）；x0（t）：R+→（0,a）is H¨older continuous.They proved that，if m＞1 or p＞1 or nq＞（m-1）（p-1），the classical solutions blow up for large initial data and are global for small initial data.Conversely，for m＜1，p＜1 and nq＜（m-1）（p-1），all solutions are global.Moreover，under the assumption α=β∈（0,1），（xαu00（x））0≤M1，（xαv00（x））0≤M2for x∈（0,a），the blow-up set，simultaneous blow-up phenomena and their sharp blow-up rates are discussed.

For α=β=0，the parabolic systems have been extensively studied.The authors refer the interested readers to［5-19］and the papers cited there for the local，localized and nonlocal parabolic systems with respect to blow-up criteria，rates，profiles and even boundary layers estimates，etc.

The nonlinear nonlocal sources in（1.1）are much more complicated than the ones of（1.3）and（1.4）in［3-4］，which arouse more difficulties.Motivated by the works［2-4］，we care about the critical blow-up exponent and uniform blow-up behavior near the blow-up time，including blow-up profiles and blow-up set of system（1.1）.

This paper is arranged as follows：in the next section，we show the existence and uniqueness of local classical solutions also with the comparison principle.At Section 3，we show the critical blow-up exponents for blow-up and global solutions.The simultaneous blow-up criteria of solutions and their uniform blow-up behaviors are determined at the last section.

§2.Local Existence and Comparison Principle

In this section，we begin with a comparison principle of the following type，which can be obtained by using the standard procedures in［20］.

Proposition 2.1Let（Φ（x,t）,Ψ（x,t））∈（C（［0,a］×［0,T））TC2,1（（0,a）×（0,T）））2.If

where fi（t），i=1,2,3,4 are some continuous nonnegative functions in［0,T），then Φ（x,t）≥0 and Ψ（x,t）≥0 for（x,t）∈［0,a］×（0,T）.

The following definitions are about super-solutions and sub-solutions of system（1.1）.

Definition 2.1A pair of nonnegative functions（¯u（x,t）,¯v（x,t））is called a super-solution of system（1.1），if（¯u（x,t）,¯v（x,t））∈（C（［0,a］×［0,T））TC2,1（（0,a）×（0,T）））2and satisfies Similarly，（uu（x,t）,uv（x,t））∈（C（［0,a］×［0,T））TC2,1（（0,a）×（0,T）））2is called a sub-solution of（1.1）if it satisfies all the reversed inequalities in（2.1）.

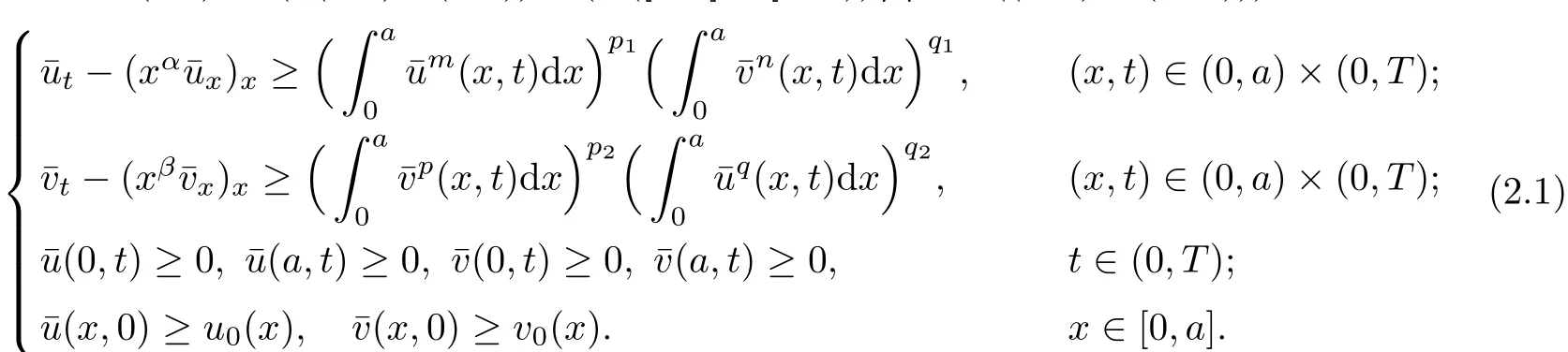
By using the similar procedures in［3，21］and combining the comparison principle of Proposition 2.1，we show the existence and uniqueness of local classical nonnegative solutions of（1.1）without proofs.

Theorem 2.1Let T be the supremum over t0for which there is a unique nonnegative solution（u（x,t）,v（x,t））∈（C（［0,a］×［0,t0））TC2,1（（0,a）×（0,t0）））2of（1.1）.Then system（1.1）has a unique nonnegative solution（u（x,t）,v（x,t））∈（C（［0,a］×［0,T））TC2,1（（0,a）×（0,T）））2. If T＜+∞，then

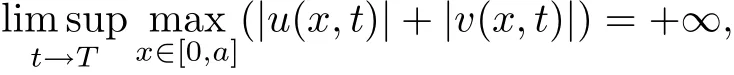
that is，（u,v）blows up in finite time.

§3.Critical Blow-up Exponents

In this section，we consider the global existence and blow-up phenomena of the solution for（1.1）.

Theorem 3.1If mp1＜1,pp2＜1 and nq1qq2≤（1-mp1）（1-pp2）,（3.1）then all solutions of system（1.1）exist globally.

ProofIntroduce the two eigenvalue problems

By another transformation y（x）=φ（z）with，（3.2）becomes

where b=a2-α2.It can be found that（3.4）is a Bessel equation whose general solutions are given by

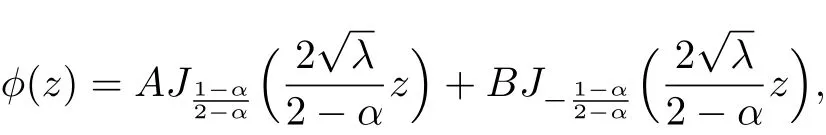
where A and B are arbitrary constants，andanddenote the Bessel functions of the first kind of orders，respectively.Let λ1be the first root ofBy Mclachlan［22］，it is positive.It is obvious that λ1is the first eigenvalue of problem（3.2）；also we can easily obtain the corresponding eigenfunction

which is positive for x∈（0,a），where k1＞0 is arbitrary.So we can choose ϕ1（x）such that.Denotethen C1＞0，d1＞0. Analogously，we consider the eigenvalue problem（3.3）.By using the same method as above， letµ1be the first root of.By Mclachlan（3.3），it is positive.It is obvious that µ1is the first eigenvalue of problem（3.3）.Similarly，we can easily obtain the corresponding eigenfunction

which is positive for x∈（0,a），where k2＞0 is arbitrary.So we can choose ψ1（x）such that.Denoteand，then C2＞0，d2＞0. By using（3.1），we have

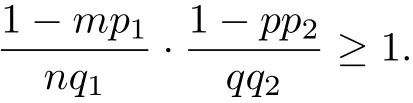
Thus we can choose two constants r1,r2＞1 such that

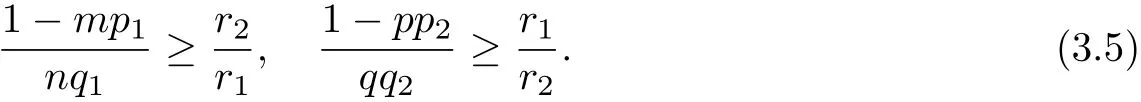
Let s（t）be the unique solution of the ODE problem

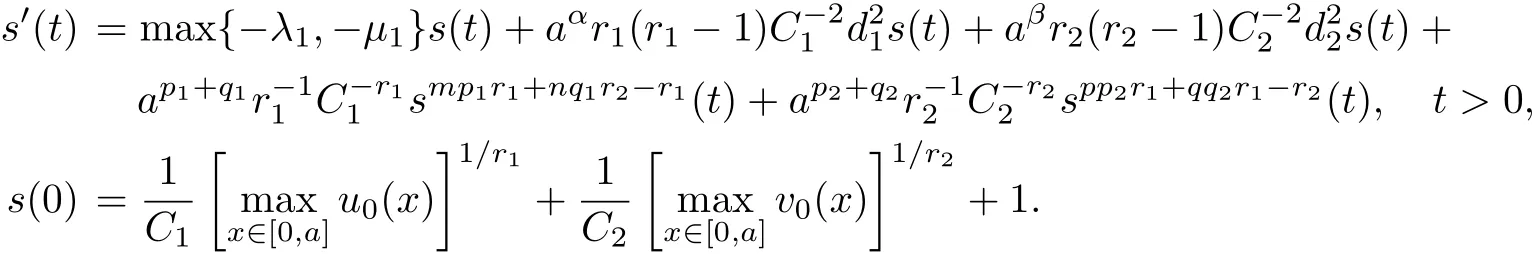
By（3.8），we know that mp1r1+nq1r2-r1+1≤1，pp2r2+qq2r1-r2+1≤1.Hence s（t）exists globally.

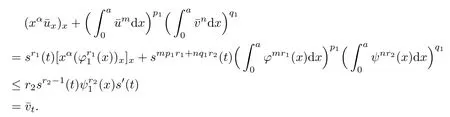
It can be seen that

and

Then we get（¯u,¯v）≥（u,v）by the comparison principle.Hence（u,v）exists globally.

Theorem 3.2If one of the following conditions holds，

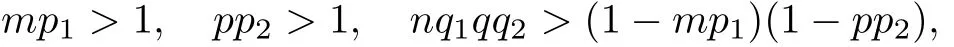
then the solution of problem（1.1）exists globally for small initial data and blows up in finite time for large initial data，respectively.

ProofGlobal existence case.

The proof can be finished by using the procedure in［23］.We prove the case mp1＞1 for completeness.Let

be the unique solutions of the following elliptic problems

respectively.A direct computation yields that there exist positive constants C3and C4such that

Noticing mp1＞1 and pp2＞1，it is easy to verify that there exist two positive constants b1and b2such that

b1＞ap1+q1［b1（1+C3）］mp1［b2（1+C4）］nq1,b2＞ap2+q2［b1（1+C3）］qq2［b2（1+C4）］pp2. Define

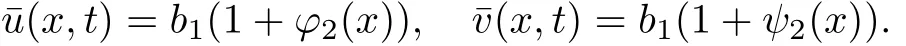
Then we have

By the comparison principle，we obtain that（u,v）≤（¯u,¯v）provided that u0（x）≤aϕ2（x），v0（x）≤aψ2（x）.Therefore，（u,v）remains global.

Blow-up case.

Let λ1，λ2be the first eigenvalues of the eigenvalue problems（3.2）and（3.3），respectively，and ϕ1（x）＞0，ψ1（x）＞0 be the corresponding eigenfunctions，respectively，normalized by.Assume mp1＞1.

Since qq2＞0，we can choose r3，r4∈（0,1）such that pp2r4+qq2r3-r4＞0，mp1r3+ nq1r4-r3＞0.Set γ=min｛pp2r4+qq2r3-r4+1,mp1r3+nq1r4-r3+1｝，then γ＞1.

Let s（t）be the unique solution of the following ODE problem

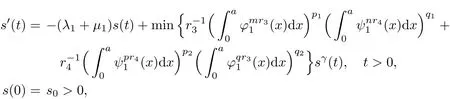
then s（t）blows up in finite time with large s0.

Similarly，we obtain

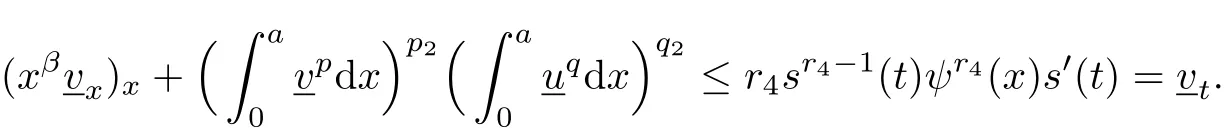
By the comparison principle，we getand hence（u,v）blows up.For the case of pp2＞1，the proof is similar.

Assume 0＜mp1≤1，0＜pp2≤1 and nq1qq2＞（1-mp1）（1-pp2）.

Noticing nq1＞0，qq2＞0，there exist two positive constants r5，r6such that

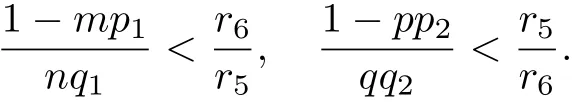
Let γ：=min｛r5mp1+r6nq1-r5+1,r6pp2+r5qq2-r6+1｝.Then γ＞1.Set=）are defined above.The left arguments are the same as those of the case for mp1＞1.

§4.Uniform Blow-up Behavior

In this section，we deal with the uniform blow-up behavior including blow-up set and uniform blow-up profiles.We denote by T∗the blow-up time of（u（x,t）,v（x,t））.Assume α=β∈［0,1）.

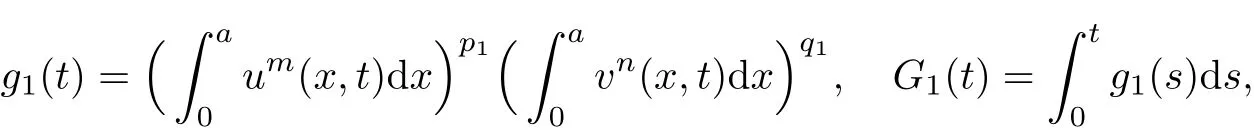
and we use the notation w1（t）～w2（t），t→T fo.In order to prove the uniform blow-up behavior，we need the following assumptions in the sequel.

（H）（xαu0x（x））x≤M1,（xαv0x（x））x≤M2in（0,a）for some constants M1,M2＞0.

We introduce three lemmas at first.

Lemma 4.1The solution（u（x,t）,v（x,t））of system（1.1）satisfies（xαux（x））x≤M1，（xαvx（x））x≤M2for（x,t）∈（0,a）×（0,T∗）.

ProofSet w1（x,t）=（xαux（x,t））x-M1，w2（x,t）=（xαvx（x,t））x-M2.After computation，we have

w1t（x,t）-（xαw1x（x,t））x=0,w2t（x,t）-（xαw2x（x,t））x=0,（x,t）∈（0,a）×（0,T∗）. Since w1（x,0）=（xαux（x,0））x-M1≤0 in（0,a）and

By the maximum principle，w1（x,t）≤0 in（0,a）×（0,T∗）.That is to say，（xαux（x））x≤M1in（0,a）×（0,T∗）.Similarly，we have（xαvx（x））x≤M2in（0,a）×（0,T∗）.

The following two lemmas can be obtained by［12，3］.We show the results without proofs.

Lemma 4.2Let（u（x,t）,v（x,t））be a blow-up solution of system（1.1）and assume that u and v blow up simultaneously at time T∗＜+∞.Then

Lemma 4.3Assume u and v blow up simultaneously at T∗＜+∞.Then

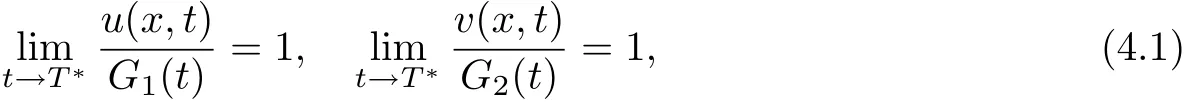
uniformly on［c,d］⊂（0,a）.Especially，if u（or v）blows up alone，then

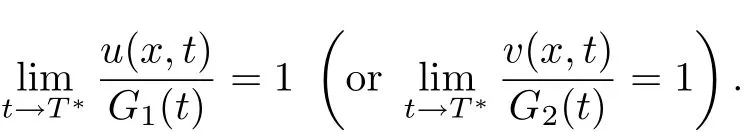
Accordingly，we have the blow-up set results.

Theorem 4.1Assume the solution（u,v）of（1.1）blows up in finite time.Then the blow-up set is the whole domain.

In fact，after integrating the differential equation in（1.1）over（0,t），we have

Obviously，（u,v）blows up almost everywhere in（0,a）by lemmas 4.2 and 4.3.

Now，we give some exponent regions for the existence of simultaneous blow-up phenomena.

Theorem 4.2Let（u,v）be the solution of system（1.1）.If qq2≥mp1-1＞0 and nq1≥pp2-1＞0，then simultaneous blow-up occurs for large initial data.

ProofBy using Lemma 4.3，we know that if u（or v）blows up at the time T∗，then u～G1（t）（or v～G2（t））.We assume that u blows up at the time T∗，while v is bounded.Then

and hence we have G1（t）～c（T∗-t）for some constant c＞0.By using（1.1），we have

Due to qq2≥mp1-1＞0，one can find that G2（t）blows up at the time T∗.According to Theorem 4.1 in［6］，we knowa contradiction.So u and v blow up simultaneously for large initial data.

Till now，we determine the uniform blow-up profile of system（1.1）under the condition of simultaneous blow-up.

Theorem 4.3Let（u,v）be a simultaneous blow-up solution of system（1.1）.

（i）If qq2＞mp1-1＞0 and nq1＞pp2-1＞0，then

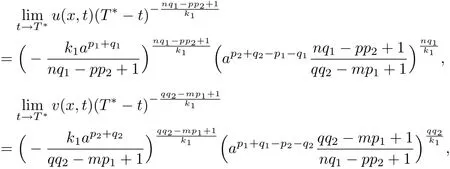
uniformly on any compact subsets of（0,a），with k1：=（pp2-1）（mp1-1）-nq1qq2；（ii）If qq2＞mp1-1＞0 and nq1=pp2-1＞0，then

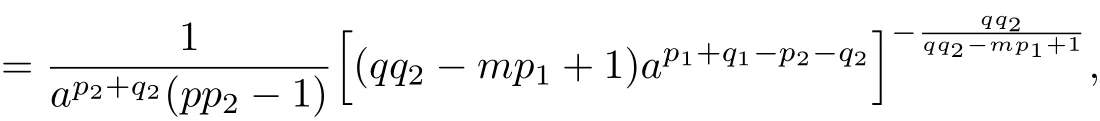
uniformly on any compact subsets of（0,a）；

（iii）If qq2=mp1-1＞0 and nq1＞pp2-1＞0，then

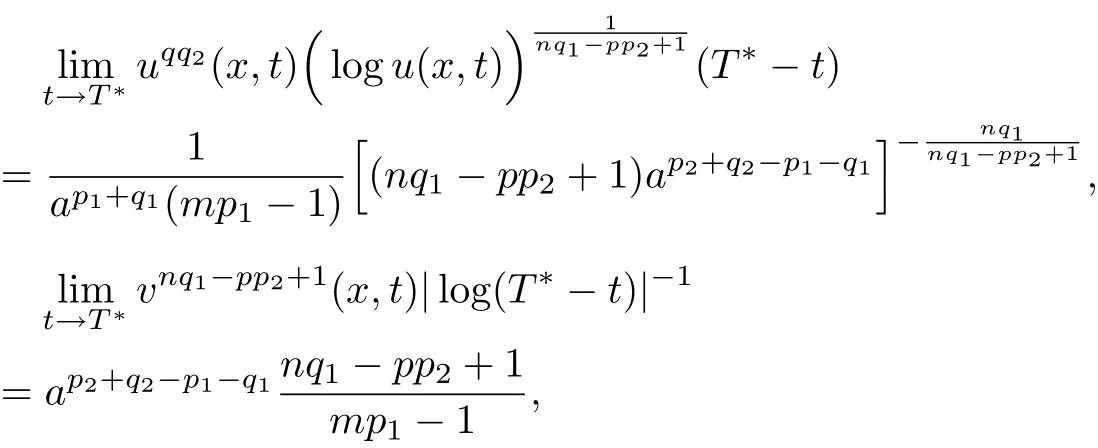
uniformly on any compact subsets of（0,a）；

（iv）If qq2=mp1-1＞0 and nq1=pp2-1＞0，then

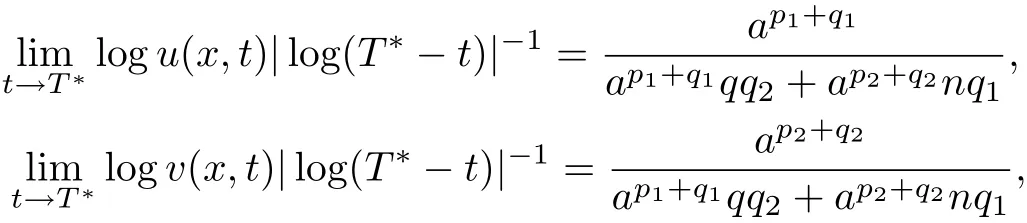
uniformly on any compact subsets of（0,a）. ProofFrom Lemma 4.3，we obtain

and

for some constant C＞0，x∈（0,a），as t is sufficiently close to T∗.

By Lebesgue's dominated convergence theorem，we have

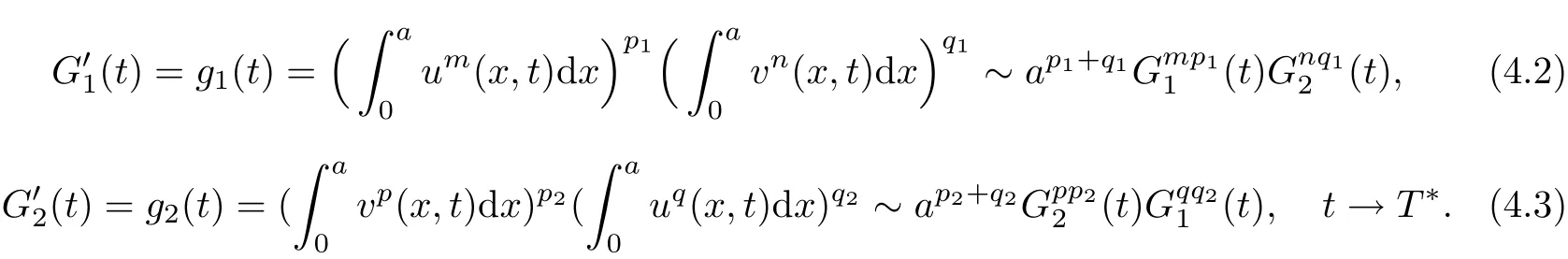
Combining（4.2）～（4.3），we obtain

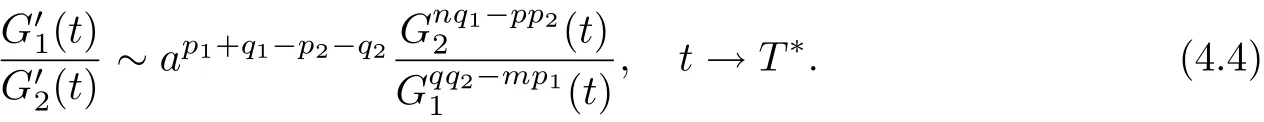
（i）In this case，from（4.4），we have

By（4.2）～（4.6），we obtain

Integrating（4.7）and（4.8）over（t,T∗）yields

We obtain our conclusion by using（4.1）and k1=-nq1qq2+（pp2-1）（mp1-1）.（ii）In this case，from（4.4），we yield

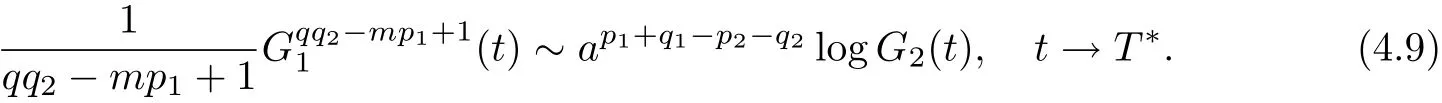
Combining（4.3）and（4.9），we obtain

Integrating（4.10）over（t,T∗），we have

Since pp2＞1，the integrais convergent and

Noticing

we have

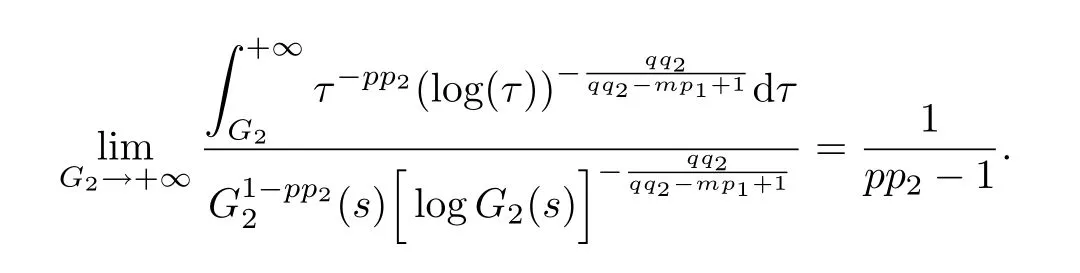
Thus

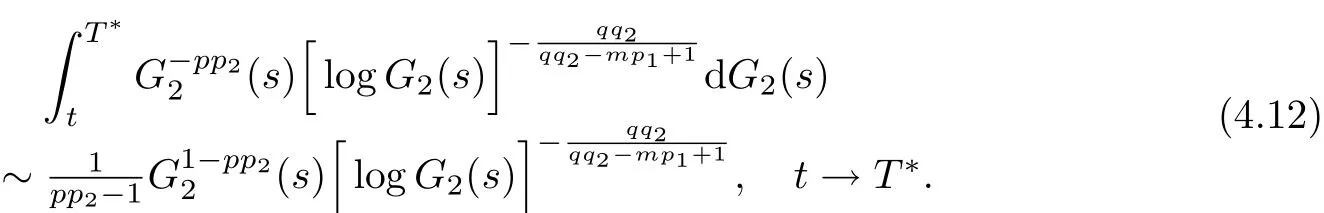
By（4.11）and（4.12），we obtain

From the fact that v（x,t）～G2（t）as t→T∗uniformly on any compact subsets of（0,a），we obtain logv～logG2as t→T∗uniformly on any compact subsets of（0,a）.Therefore，

that is，

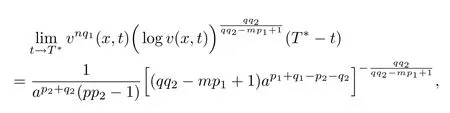
uniformly on any compact subsets of（0,a）by nq1=pp2-1＞0. Combining（4.9）and（4.13），we have

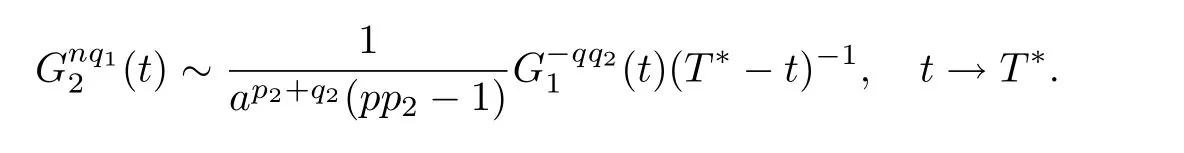
Thus，we have

Integrating（4.14）over（t,T∗），we obtain

We complete our proof by using（4.1）and nq1=pp2-1＞0.（iii）The proof of this case is similar to（ii），so we omit it.（iv）In this case，from（4.4），we yield

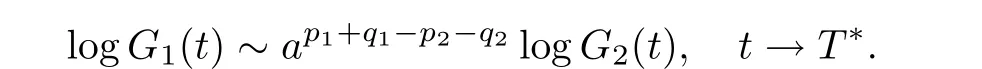
Integrating（4.2）and（4.3）over（t,T∗），we have

Thus we obtain

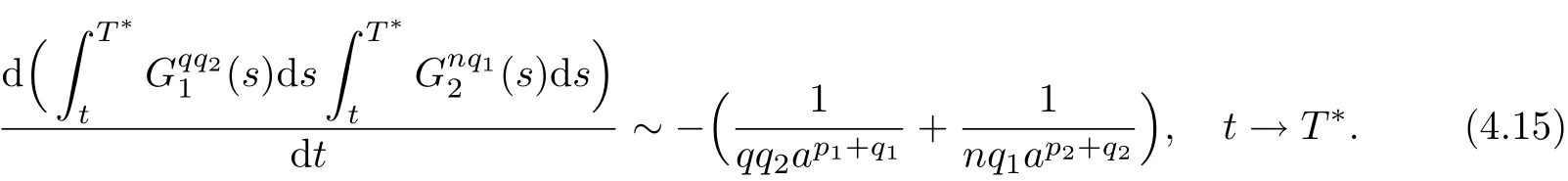
Noticing

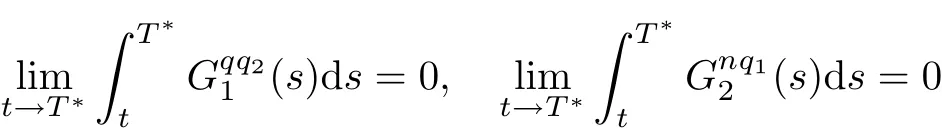
and integrating（4.15）over（t,T∗），we obtain

that is，

Combining this with（4.2）～（4.3）and noticing qq2=mp1-1，nq1=pp2-1，we obtain

Therefore，we obtain

We complete our proof by using（4.1）.

AcknowledgementThe authors would like to express their thanks to the Editors and the Reviewers for their helpful suggestions to improve this paper.

［References］

［1］CHAN Chiu-yeung，CHEN Ching-shyang.A numerical method for semilinear singular parabolic quenching problem［J］.Quart Appl Math，1989，47：45-57.

［2］CHEN You-peng，LIU Qi-lin，XIE Chun-hong.The blow-up properties for a degenerate semilinear parabolic equation with nonlocal source［J］.Appl Math J Chinese Univ，2002，17B：413-424.

［3］PENG Cong-ming，YANG Zuo-dong，XIE Bao-li.Global existence and blow-up for the degenerate and singular nonlinear parabolic system with a nonlocal source［J］.Nonlinear Analysis，2010，72：2474-2487.

［4］ZHOU Jun，MU Chun-lai.Global existence and blow-up for weakly coupled degenerate and singular parabolic equations with localized source［J］.Z Angew Math Phys，2011，62：47-66.

［5］FRIEDMAN A，MCLEOD B.Blow-up of positive solutions of semilinear heat equations［J］.Indiana Univ Math J，1985，34：425-447.

［6］GIGA Y，KOHN R V.Asymptotically self-similar blow-up of semilinear heat equations［J］.Comm Pure Appl Math，1985，38：297-319.

［7］LI Feng-jie，LIU Bing-chen，ZHENG Si-ning.Optimal conditions of non-simultaneous blow-up and uniform blow-up profiles in localized parabolic equations［J］.Nonlinear Anal，2010，72：867-875.

［8］CUI Gao-zhong，GAO Yan-ling，GUO Cong-zhou.Blow-up for a class of degenerate reaction-diffusion equation with nonlocal source［J］.Chin Quart J of Math，2010，25（3）：352-359.

［9］SAMARSKII A A，GALATIONOV V A，KURDYNUMOV A P.Blow-up in Quasilinear Parabolic Equations［M］.Berlin：Walter de Gruyter，1995.

［10］GALATIONOV V A，LEVINE H A.A general approach to critical Fujita exponents in nonlinear parabolic problems［J］.Nonlinear Anal，1998，34：1005-1027.

［11］LI Fu-cai，HUANG Shu-xiang，XIE Chun-hang.Global existence and blow-up of solutions to a nonlocal reaction-diffusion system［J］.Discrete Contin Dyn Syst，2003，9：1519-1532.

［12］SOUPLER P.Uniform blow-up profile and boundary behavior for diffusion equations with nonlocal nonlinear source［J］.J Differential Equations，1999，153：374-406.

［13］BEBERNES J，BRESSAN A，LACEY A.Total blow-up versus single point blow up［J］.J Differential Equations，1988，73：30-44.

［14］SOUPLET P.Blow-up in nonlocal reaction-diffusion equations［J］.SIAM J Math Anal，1998，29：1301-1334.［15］WANG Ming-xin，WANG Yuan-ming.Properties of positive solutions for non-local reaction-diffusion problems［J］.Math Methods Appl Sci，1996，19：1141-1156.

［16］GUO Jong-sheng，HU Bei.The profile near quenching time for the solution of a singular semilinear heat equation［J］.Proc Edinb Math Soc，1997，40：437-456.

［17］LI Hui-ling，WANG Ming-xin.Uniform blow-up profiles and boundary layer for a parabolic system with localized nonlinear reaction terms［J］.Sci China，2005，48A：185-197.

［18］LI Hui-ling，WANG Ming-xin.Blow-up properties for parabolic systems with localized nonlinear sources［J］. Appl Math Letters，2004，17：771-778.

［19］LI Hui-ling，WANG Ming-xin.Properties of blow-up solutions to a parabolic system with nonlinear localized terms［J］.Discrete Contin Dyn Syst，2005，13：683-700.

［20］PAO Chia-ven.Nonlinear Parabolic and Elliptic Equations［M］.New York：Plenum，1992.

［21］CHADAM J，PEIRCE A，YIN Hong-ming.The blowup property of solutions to some diffusion equation with localized nonlinear reactions［J］.J Math Anal Appl，1992，169：313-328.

［22］MCLACHLAN N W.Bessel Functions for Engineers［M］.London：Clarendon Press，Oxford University Press，1955.

［23］WANG Ming-xin.Global existence and finite time blow-up for a reaction-diffusion system［J］.Z Angew Math Phys，2000，51：160-167.

O175.26Document code：A

date：2014-03-27

Supported by the National Natural Science Foundation of China（11201483）；Supported by the Natural Science Foundation of Shandong Province；Supported by the Fundamental Research Funds for the Central Universities

Biography：LIU Bing-chen（1976-），male，native of Weifang，Shandong，an associate professor of China University of Petroleum，Ph.D.，engages in partial differential equations.