Vertex-distinguishing IE-total Colorings of Complete Bipartite Graphs K8,n

SHI Jin，CHEN Xiang-en

（College of Mathematics and Statistics，Northwest Normal University，Lanzhou 730070，China）



Vertex-distinguishing IE-total Colorings of Complete Bipartite Graphs K8,n

SHI Jin，CHEN Xiang-en

（College of Mathematics and Statistics，Northwest Normal University，Lanzhou 730070，China）

Let G be a simple graph.An IE-total coloring f of G is a coloring of the vertices and edges of G so that no two adjacent vertices receive the same color.For each vertex x of G，let C（x）be the set of colors of vertex x and edges incident to x under f.For an IE-total coloring f of G using k colors，if C（u）/=C（v）for any two different vertices u and v of G，then f is called a k-vertex-distinguishing IE-total-coloring of G or a k-VDIET coloring of G for short.The minimum number of colors required for a VDIET coloring of G is denoted by Xievt（G）and is called vertex-distinguishing IE-total chromatic number or the VDIET chromatic number of G for short.The VDIET colorings of complete bipartite graphs K8,nare discussed in this paper.Particularly，the VDIET chromatic number of K8,nare obtained.

complete bipartite graphs；IE-total coloring；vertex-distinguishing IE-total coloring；vertex-distinguishing IE-total chromatic number

2000 MR Subject Classification：05C15

Article ID：1002—0462（2016）02—0147—08

Chin.Quart.J.of Math.

2016，31（2）：147—154

§1.Introduction

The vertex distinguishing proper total colorings of graphs are introduced and studied in［1］.After studying the vertex distinguishing proper total colorings of complete graph，complete bipartite graph，star，wheel，fan，path and cycle，a conjecture was proposed in［1］：let µ（G）=min

For a total coloring（proper or not）f of G and each vertex x of G，let C（x）be the set（not multiset）of colors of vertex x and edges incident to x under f.Supposeis the complementary set of C（x）in the set of all colors we use in coloring f.

If f is a proper total coloring of graph G using k colors and for any u，v∈V（G），u/=v，we have C（u）/=C（v），then f is called a k-vertex-distinguishing total-coloring or a k-VDTC.The number min｛k：G has a k-VDTC｝is called the vertex-distinguishing total chromatic number of a graph G and is denoted by Χvt（G）.

In the following we consider a kind of not necessarily proper total coloring which is vertex distinguishing.An IE-total coloring f of a graph G is an assignment of colors to the vertices and edges of G such that no two adjacent vertices receive the same color.If f is an IE-total coloring of graph G using k colors and for any u，v∈V（G），u/=v，we have C（u）/=C（v），then f is called a k-vertex-distinguishing IE-total-coloring or a k-VDIET coloring.The number min｛k：G has a k-VDIET coloring｝is called the vertex-distinguishing IE-total chromatic number of a graph G（VDIET chromatic number of G briefly）and is denoted by

For a graph G，let nidenote the number of vertices of degree i，δ≤i≤∆.Let ξ（G）= min

In［2］，the VDIET colorings of complete bipartite graphs were discussed and by using the basic results in［2］we obtained easily VDIET chromatic numbers of complete graphs Km,n（m＜n）for m=1,2,···,7.The VDIET chromatic numbers of K4,nand K5,nare also obtained in［3］and［4］respectively without relying on the basic results in［2］.In this paper we will consider the VDIET colorings of complete bipartite graphs K8,n.

For other notations and terminologies we can refer to［3］.

§2.Preliminaries

For a complete bipartite graph Km,n（1≤m＜n），ξ（Km,n）is the minimum positive integer l such that

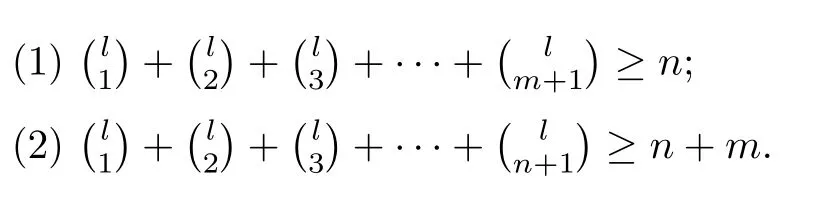
The following Lemma 1，Lemma 2 and Lemma 3 have been proved in［2］. Lemma 1［2］Let m≥1，n＞2m+2-m-2.Then Χievt（Km,n）=k when

Lemma 2［2］

Lemma 3［2］Let s be the minimum positive integer such that 2s-1≥3m.When 2r-2m-1＜n≤2r+1-2m-1，we have，where r=m+1,m,m-1 andr≥s.

Conjecture 4［2］For a simple graph G，if its（proper vertex coloring）chromatic number Χ（G）≤4，then we have

§3.Main Results

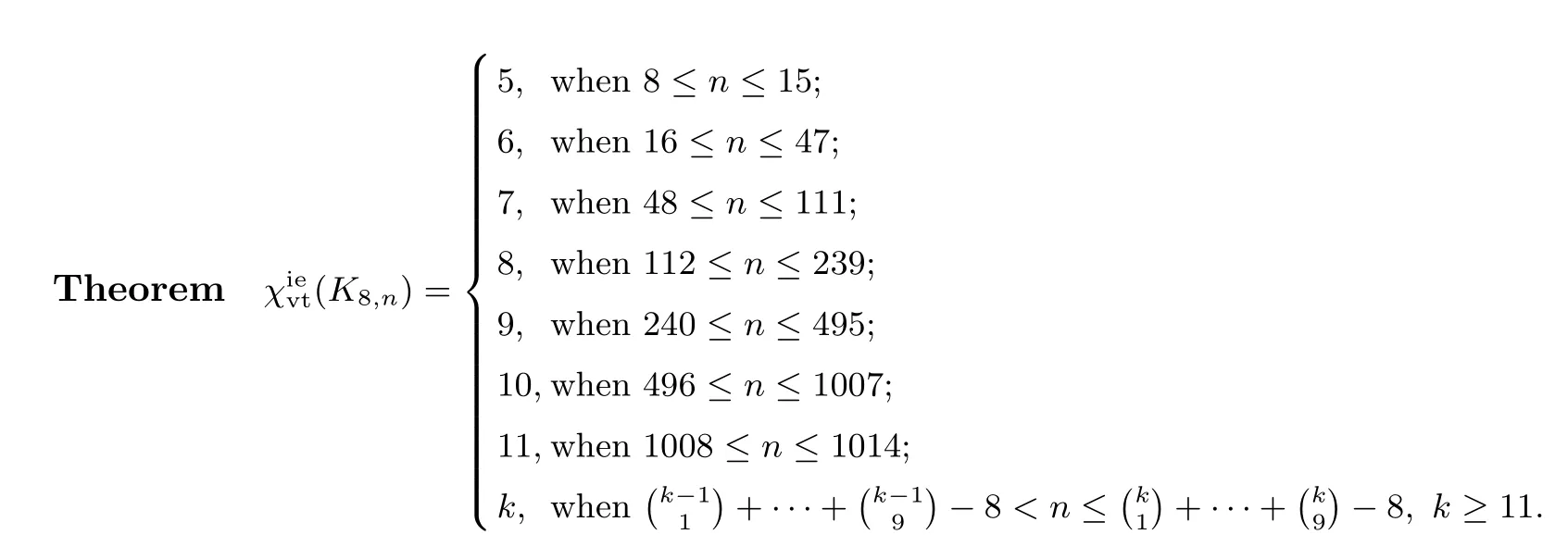
ProofBy Lemma 1，Lemma 2 and Lemma 3 we know that the theorem is valid in each case when n≥112.Now we consider the case 8≤n≤111.

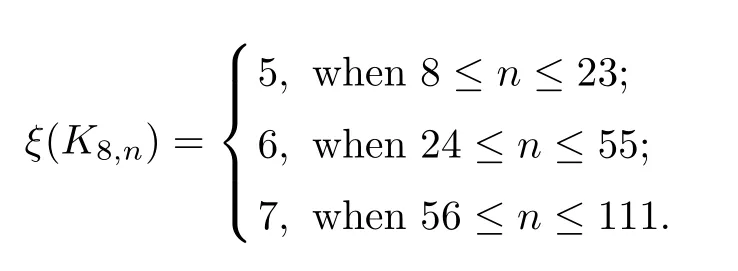
Let V（K8,n）=｛u1,u2,···,u8,v1,v2,···,vn｝and E（K8,n）=｛uivj：1≤i≤8,1≤j≤n｝.

We will prove K8,ndoes not have a 5-VDIET coloring when 16≤n≤23.If not，suppose g is a 5-VDIET coloring of K8,n（16≤n≤23）using colors 1，2，3，4，5.First we give four claims as follows.

Claim 1|C（ui）|≥2，i=1,2,3,···,8.

ProofSuppose the claim is not true，without loss of generality，we assume C（u1）=｛1｝，then 1∈C（vj）,j=1,2,···,n（16≤n≤23）.Thusare not available for any vertex and at most one of them is an empty set.Thus there are at most 25-1-（n-1）≤16 nonempty subsets of｛1,2,3,4,5｝which can become the color sets of vertices u1,u2,···,u8,v1,v2,···,vn.These subsets can not distinguish n+8（16≤n≤23）vertices，this is a contradiction.

Claim 2|C（vj）|≥2，j=1,2,3,···,n,16≤n≤23.

ProofSuppose the claim is not true，without loss of generality，we assume C（v1）=｛1｝，then 1∈C（ui）,i=1,2,···,8.Thusare not available for any vertex and at most one of them is an empty set.Then there are at most 25-1-（8-1）-1=23 nonempty subsets of｛1,2,3,4,5｝which can become the color sets of vertices u1,u2,···,u8,v1,v2,···,vn.These subsets can not distinguish n+8（16≤n≤23）vertices，this is a contradiction.

Claim 3C（u1）TC（u2）T···TC（u8）=∅.

Proof Suppose the claim is not true，without loss of generality，we assume 1∈C（ui），i=1,2,···,8.Then｛1｝,are not available for any vertex and at most one of them is an empty set.Thus there are at most 25-1-8=23 nonempty subsets of｛1,2,3,4,5｝which can become the color sets of vertices u1,u2,···,u8,v1,v2,···,vn.These subsets can not distinguish n+8（16≤n≤23）vertices，this is a contradiction.

ProofSuppose the claim is not true，without loss of generality，we assume 1∈C（vj），j=1,2,···,n.Then｛1｝,）are not available for any vertex and at most one of them is an empty set.Thus there are at most 25-1-n≤15（16≤n≤23）nonempty subsets of｛1,2,3,4,5｝which can become the color sets of vertices u1,u2,···,u8,v1,v2,···,vn. These subsets can not distinguish n+8（16≤n≤23）vertices，this is a contradiction.

By above claims，five 1-subsets of｛1,2,3,4,5｝are not available for any vertex.The remaining 26 nonempty subsets of｛1,2,3,4,5｝can not distinguish n+8 vertices when 19≤n≤23，this is a contradiction.So we consider n=16,17,18 in the following.

Let t=|｛g（u1）,g（u2）,···,g（u8）｝|，without loss of generality，we assume that｛g（u1）,g（u2）, ···,g（u8）｝=｛1,2,···,t｝，by Claim 3 and Claim 4，we know that t=2 or t=3.

Case 1t=2，｛g（u1）,g（u2）,···,g（u8）｝=｛1,2｝.

Of course｛1,2｝/∈｛C（v1）,C（v2）,···,C（vn）｝.If｛1,2｝∈｛C（u1）,C（u2）,···,C（u8）｝，then 1∈C（vj），j=1,2,···,n，or 2∈C（vj），j=1,2,···,n.Thus｛3,5｝，｛3,4｝，｛4,5｝，｛3,4,5｝are not the color sets of any vertex.So there are at most 25-1-5-4=22 nonempty subsets of｛1,2,3,4,5｝can become the color sets of vertices u1,u2,···,u8,v1,v2,···,vn，but the 22 subsets can not distinguish n+8（n=16,17,18）vertices.This is a contradiction.So｛1,2｝is not available for any vertex.

If|C（ui）|≥3，i=1,2,···,8，thenare not available for any vertex and at most one of them is an empty set.So there are at most 25-1-7-1=23 nonempty subsets can be the color sets of vertices u1,u2,···,u8,v1,v2,···,vn.This is a contradiction because 23 subsets can not distinguish n+8（n=16,17,18）vertices.

Thus there exists a vertex ui0with|C（ui0）|=2.Since｛1,2｝is not available for any vertex，without loss of generality，we assume C（ui0）=｛1,4｝，then 1∈C（vj），j=1,2,···,n，or 4∈C（vj），j=1,2,···,n.Then｛3,5｝is not available for any vertex.So there are at most 25-1-5-1-1=24 nonempty subsets can be the color sets of vertices u1,u2,···,u8,v1,v2,···,vn. This is a contradiction because 24 subsets can not distinguish n+8（n=17,18）vertices.

Then we consider the case n=16.In this case，the remaining 24 subsets must be all used if K8,nhas a 5-VDIET coloring.Since C（ui）TC（vj）/=∅，each one of the remaining 24 subsets which have no common element with some C（ui）is in｛C（u1）,C（u2）,···,C（u8）｝.Since｛1,2｝is not available for any vertex，we have assumed C（ui0）=｛1,4｝，thus｛2,3,5｝，｛2,5｝，｛2,3｝belong to｛C（u1）,C（u2）,···,C（u8）｝.From｛2,5｝is in｛C（u1）,C（u2）,···,C（u8）｝，we knowthat｛1,3,4｝，｛1,3｝，｛3,4｝belongto｛C（u1）,C（u2）,···,C（u8）｝.Similarly，we can obtain that｛1,4,5｝，｛1,5｝，｛4,5｝，｛2,4,5｝，｛1,2,5｝，｛2,3,4｝，｛1,2,3｝，｛2,4｝belong to｛C（u1）,C（u2）,···, C（u8）｝.As｛g（u1）,g（u2）,···,g（u8）｝=｛1,2｝，we know that｛3,4｝，｛4,5｝are not available for any vertex，Then there are 13 subsets in｛C（u1）,C（u2）,···,C（u8）｝and the left subsets are not enough to color vj，1≤j≤n.This is a contradiction.

Case 2t=3，｛g（u1）,g（u2）,···,g（u8）｝=｛1,2,3｝.Then｛g（v1）,g（v2）,···,g（vn）｝=｛4,5｝.Similarly，｛4,5｝is not available for any vertex.

Similar to Case 1，we know that there exists a vertex vj0with|C（vj0）|=2.Since｛4,5｝is not available for any vertex，without loss of generality，we assume C（vj0）=｛1,4｝，then 1∈C（ui）or 4∈C（ui），i=1,2,···,8.Then｛2,3｝is not available for any vertex.So there are at most 25-1-5-1-1=24 nonempty subsets can be the color sets of vertices u1,u2,···,u8,v1,v2,···,vn.This is a contradiction because 24 subsets can not distinguish n+8（n=17,18）vertices.

Then we consider the case n=16.In this case，the remaining 24 subsets must be all used if K8,nhas a 5-VDIET coloring.Since｛4,5｝is not available for any vertex，We have assumed C（vj0）=｛1,4｝，thus｛2,3,5｝，｛2,5｝，｛3,5｝belong to｛C（v1）,C（v2）,···,C（vn）｝. From｛3,5｝is in｛C（v1）,C（v2）,···,C（vn）｝，we know that｛1,2,4｝，｛1,2｝，｛2,4｝belong to｛C（v1）,C（v2）,···,C（vn）｝.But from｛g（v1）,g（v2）,···,g（vn）｝=｛4,5｝，we know that｛1,2｝can not belong to｛C（v1）,C（v1）,···,C（vn）｝.This is a contradiction.

Thus we have proved that K8,ndo not have a 5-VDIET coloring（16≤n≤23）.

We will prove K8,ndoes not have a 6-VDIET coloring（48≤n≤55）in the following.

Suppose K8,nhas a 6-VDIET coloring（48≤n≤55）.Similar toTclaims T1-4 wTe can obtain that.As six 1-subsets can not become color sets of any vertex，the remaining 57 nonempty subsets of｛1,2,3,4,5,6｝can not distinguish n+8 vertices when 50≤n≤55，this is a contradiction.So we consider n=48,49 in the following.Suppose|｛g（u1）,g（u2）,···,g（u8）｝|=t.

Since|C（ui）|≥2，|C（vj）|≥2，we know that 2≤t≤6-2，then t=2 or t=3 or t=4.

Case 1t=2，we may assume｛g（u1）,g（u2）,···,g（u8）｝=｛1,2｝，of course｛1,2｝/∈｛C（v1）,C（v2）,···,C（vn）｝.If｛1,2｝∈｛C（u1）,C（u2）,···,C（u8）｝，then 1∈C（vj）or 2∈C（vj）. Thus｛3,4｝，｛3,5｝，｛3,6｝，｛4,5｝，｛4,6｝，｛5,6｝，｛3,4,5｝，｛3,4,6｝，｛3,5,6｝，｛4,5,6｝，｛3,4,5,6｝are not available for any vertex.So there are at most 26-1-6-11=46 nonempty subsets can become color sets of u1,u2,···,u8,v1,v2,···,vn.This is a contradiction because 46 subsets can not distinguishing n+8（n=48,49）vertices，thus｛1,2｝is not available for any vertex.

If|C（ui）|≥4，i=1,2,···,8，thenare not available for any vertex and at most one of them is an empty set.Thus there are at most 26-1-7-1=55 nonempty subsets left and the 55 subsets can not distinguishing n+8（n=48,49）vertices.This is a contradiction.

If|C（ui）|≥3，i=1,2,···,8，there exists a vertex ui0with|C（ui0）|=3，without loss ofgenerality，we assume C（ui0）=｛1,3,4｝，then 1∈C（vj）or 3∈C（vj）or 4∈C（vj），｛5,6｝is not available for any vertex.So there are at most 26-1-6-1-1=55 nonempty subsets which can become color sets.But 55 subsets can not distinguishing n+8（n=48,49）vertices. So this is a contradiction.

Note that|C（ui）|≥2，i=1,2,···,8，therefore there exists a vertex ui0such that|C（ui0）|= 2，as｛1,2｝is not available for any vertex，we may assume that C（ui0）=｛1,3｝，then 1∈C（vj）or 3∈C（vj），j=1,2,···,n，thus｛4,5｝，｛4,6｝，｛5,6｝，｛4,5,6｝can not be color sets of any vertex.So there are at most 26-1-6-4-1=52 nonempty subsets available.This is a contradiction because 52 subsets can not distinguishing n+8（n=48,49）vertices.

Case 2t=3，we may assume｛g（u1）,g（u2）,···,g（u8）｝=｛1,2,3｝，as C（v1）TC（v2）T··· TC（vn）=∅，then|｛g（v1）,g（v2）,···,g（vn｝|≥2，thus|｛g（v1）,g（v2）,···,g（vn）｝|=2 or 3.

（a）When|｛g（v1）,g（v2）,···,g（vn）｝|=2，we may assume｛g（v1）,g（v2）,···,g（vn）｝=｛4,5｝.

If|C（vj）|≥4，j=1,2,···,n，are not available for any vertex. So there are at most 26-1-（n-1）≤16（n=48,49）nonempty subsets available.It is a contradiction.

If|C（vj）|≥3，j=1,2,···,n，there exists a vertex vj0with|C（vj0）|=3，without loss of generality，we assume C（vj0）=｛3,4,6｝，then 3∈C（ui）or 4∈C（ui）or 6∈C（ui），we can

get that the three 2-subsets of）are not available for any vertex.So there are at most 26-1-6-3=54 nonempty subsets.This is a contradiction because 54 subsets can not distinguishing n+8（n=48,49）vertices.

Thus from|C（vj）|≥2，j=1,2,···,n，we know that there exists a vertex vj0such that |C（vj0）|=2，thenat most contain one of color 4 and color 5. There exists three 2-subsets and a 3-subset of C（vj0）do not contain color 4 or color 5.The 4 subsets above are not available for any vertex.So there are at most 26-1-6-4=53 nonempty subsets available.This is a contradiction because 53 subsets can not distinguishing n+8（n=48,49）vertices.

（b）When|｛g（v1）,g（v2）,···,g（vn）｝|=3，then｛g（v1）,g（v2）,···,g（vn）｝=｛4,5,6｝.Similarly we can get that｛4,5,6｝is not available for any vertex.

Similar to（a），we know that there exists a vertex vj0such that|C（vj0）|=2.

（i）If the C（vj0）is a 2-subset of｛4,5,6｝，without loss of generality，we assume C（vj0）=｛4,5｝，then｛1,2｝，｛2,3｝，｛1,3｝are not available for any vertex.Therefore there are at most 26-1-6-3=54 nonempty subsets available.This is a contradiction because 54 subsets can not distinguishing n+8（n=48,49）vertices.

（ii）If the C（vj0）which|C（vj0）|=2 is not a 2-subset of｛4,5,6｝，from every 2-subset of｛4,5,6｝is not available for any vertex，then｛4,5｝，｛4,6｝，｛5,6｝are not color sets of any vertex. So there are at most 26-1-6-3=54 nonempty subsets available.This is a contradiction because 54 subsets can not distinguishing n+8（n=48,49）vertices.

Case 3t=4，we may assume｛g（u1）,g（u2）,···,g（u8）｝=｛1,2,3,4｝，since|｛g（v1）,g（v2）,···,g（vn）｝|≥2，we know that|｛g（v1）,g（v2）,···,g（vn）｝|=2.Then｛g（v1）,g（v2）,···,g（vn）｝=｛5,6｝.

Similar to（a）of case 2，we know that there exists a vertex vj0such that|C（vj0）|=2.

When C（vj0）T｛5,6｝=｛5,6｝，thus C（vj0）=｛5,6｝.Since the six 2-subsets of｛1,2,3,4｝are not available for any vertex.So there are at most 26-1-6-6=51 nonempty subsets available.This is a contradiction because 51 subsets can not distinguishing n+8（n=48,49）vertices.

Thus we have proved K8,ndoes not have a 6-VDIET coloring when 48≤n≤55.

In the following，we will give a 5-VDIET coloring（8≤n≤15），6-VDIET coloring（16≤n≤47）and 7-VDIET coloring（48≤n≤111）of K8,n.

（1）5-VDIET coloring（8≤n≤15）of K8,n.

Let u1,u2,···,u8receive color 5.D（ui）=｛1,2,3,4,5｝｛i｝（i=1,2,3,4），D（u5）=｛1,2,5｝，D（u6）=｛1,3,5｝，D（u7）=｛1,4,5｝，D（u8）=｛1,2,3,4,5｝.Let D（vj）be the j-th term of S1. Then suppose S1=（｛1,5｝,｛2,5｝,｛3,5｝,｛4,5｝,｛1,2｝,｛1,3｝,｛1,4｝,｛1,2,3｝,｛1,2,4｝,｛1,3,4｝,｛2,3,4｝,｛2,3,5｝,｛2,4,5｝,｛3,4,5｝,｛1,2,3,4｝）.

Let vjreceive color j and uivjreceive color 5，j=1,2,3,4.For D（vj）=｛a,b｝，5≤j≤n，a＜b，we assign b to uivjif b∈D（ui），assign a to vjand its remaining incident edges.For D（vj）=｛a,b,c｝，a＜b＜c，we assign a to vj，b to uivjif b∈D（ui），c to uivjif b/∈D（ui）.For D（vj）=｛1,2,3,4｝we assign 1 to vj，2 to uivjif 2∈D（ui），3 to uivjif 2/∈D（ui），4 to uivjif 3/∈D（ui），5 to uivjif 4/∈D（ui）when i=1,2,3,4，we assign 2 to u5vj，3 to u6vj，4 to u7vj，1 to u8vj，i.e.，j=15，let u1v15,u2v15,···,u8v15receive colors 2，3，2，2，2，3，4，1 respectively. From the coloring process we know that C（ui）=D（ui），1≤i≤8，C（vj）=D（vj），1≤j≤n. Thus the above coloring is a 5-VDIET coloring of K8,n，8≤n≤15.

（2）6-VDIET coloring（16≤n≤47）of K8,n.

Let u1,u2,···,u8receive color 6.D（ui）=｛1,2,3,4,5,6｝｛i｝，i=1,2,3,4,5，D（u6）=｛1,2,3,6｝，D（u7）=｛1,2,4,6｝，D（u8）=｛1,2,3,4,5,6｝.Arrange all 47 subsets of｛1,2,3,4,5,6｝except for∅，｛1｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛4,5｝，｛3,5｝，｛2,3,4,5,6｝，｛1,3,4,5,6｝，｛1,2,4,5,6｝，｛1,2,3,5,6｝，｛1,2,3,4,6｝，｛1,2,3,4,5,6｝，｛1,2,3,6｝，｛1,2,4,6｝into a sequence S2such that the first 5 terms are｛1,6｝，｛2,6｝，｛3,6｝，｛4,6｝，｛5,6｝respectively.

Let vjreceive color j，j=1,2,3,4,5.Let uivjreceive color 6，j=1,2,3,4,5.For D（vj）=｛a,b｝，6≤j≤n，a＜b，we assign the color min［｛a,b｝TD（ui）］to uivjand a to vj.For D（vj）=｛a,b,c｝，a＜b＜c，we assign a to vj，min［D（ui）T｛a,b,c｝］to uivjwhen i=1,2,3,4,5 and max［D（ui）T｛a,b,c｝］to uivjwhen i=6,7,8.For D（vj）=｛a,b,c,d｝，a＜b＜c＜d，we assign a to vjand min［D（ui）T｛a,b,c,d｝］to uivjwhen i=1,2,3,4,5 and max［D（ui）T｛a,b,c,d｝］touivjwhen i=6,7,8.For D（vj）=｛1,2,3,4,5｝，we assign 1 to vjand let u1vj,u2vj,···,uivjreceive colors 2，3，2，2，2，3，4，5 respectively.

Then C（ui）=D（ui），1≤i≤8，C（vj）=D（vj），1≤j≤n with respect to the above coloring.Thus the above coloring is a 6-VDIET coloring of K8,n，16≤n≤47.

（3）7-VDIET（48≤n≤111）of K8,n.

Let u1,u2,···,u8receive color 7.D（ui）=｛1,2,3,4,5,6,7｝｛i｝，i=1,2,3,4,5,6，D（u7）=｛1,2,3,4,5,6,7｝，D（u8）=｛1,2,3,4,7｝.Arrange all 111 subsets of｛1,2,3,4,5,6,7｝except for∅，｛1｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7｝，｛5,6｝，｛2,3,4,5,6,7｝，｛1,3,4,5,6,7｝，｛1,2,4,5,6,7｝，｛1,2,3,5,6,7｝，｛1,2,3,4,6,7｝，｛1,2,3,4,5,7｝，｛1,2,3,4,7｝，｛1,2,3,4,5,6,7｝into a sequence S3such that the first 5 terms are｛1,7｝，｛2,7｝，｛3,7｝，｛4,7｝，｛5,7｝，｛6,7｝respectively.

Let vjreceive color j，j=1,2,3,4,5,6.Let uivjreceive color 7，j=1,2,3,4,5,6.For D（vj）=｛a,b｝，7≤j≤n，a＜b，we assign the color min［｛a,b｝TD（ui）］to uivjand a to vj.For D（vj）=｛a,b,c｝，a＜b＜c，we assign a to vj，min［D（ui）TD（vj）］to uivjwhen i=1,2,3,4,5,6，and max［D（ui）T｛a,b,c｝］to uivjwhen i=7,8.For D（vj）=｛a,b,c,d｝，a＜b＜c＜d，we assign a to vjand min［D（ui）T｛a,b,c,d｝］to uivjwhen i=1,2,3,4,5,6，and max［D（ui）T｛a,b,c,d｝］to uivjwhen i=7,8.For D（vj）=｛a,b,c,d,e｝，a＜b＜c＜d＜e，we assign a to vj，b to uivjif b∈D（ui），c to uivjif b/∈D（ui），d to uivjif c/∈D（ui），e to uivjif d/∈D（ui），a to its remaining incident edges if e/∈D（ui）.For D（vj）=｛1,2,3,4,5,6｝，we assign 1 to vjand let u1vj,u2vj,···,u8vjreceive colors 2，3，4，5，6，3，4 and 5 respectively.

From the coloring process we know that C（ui）=D（ui），1≤i≤8，C（vj）=D（vj），1≤j≤n with respect to the above coloring.Thus the above coloring is a 7-VDIET coloring of K8,n，48≤n≤111.

The above Theorem illustrates that the Conjecture 4 is true for K8,n.

［References］

［1］ZHANG Zhong-fu，QIU Peng-xiang，LI Jing-wen，et al.Vertex distinguishing total colorings of graphs［J］. Ars Combinatoria，2008，87：33-45.

［2］CHEN Xiang-en，GAO Yu-ping，YAO Bing.Vertex-distinguishing IE-total colorings of complete bipartite graphs Km,n（m＜n）［J］.Discussiones Mathematicae Graph Theory，2013，33：289-306.

［3］CHEN Xiang-en，XIN Xiao-qing，HE Wen-yu.Remarks on vertex-distinguishing IE-total coloring of complete bipartite graphs K4,nand Kn,n［J］.Journal of Mathematical Research with Applications，2012，32（2）：157-166.

［4］HE Wen-yu，CHEN Xiang-en.Vertex distinguishing IE-total chromatic numbers of complete bipartite graph K5,n［J］.Journal of Shandong University，2009，44（2）：91-96.

［5］BONDY J A，MURTY U S R.Graph Theory［M］.London：Springer，2008.

O157.5Document code：A

date：2014-04-07

Supported by the National Natural Science Foundation of China（61163037，61163054，11261046，61363060）

Biographies：SHI Jin（1990-），female，native of Tianshui，Gansu，a graduate student of Northwest Normal University，engages in graph theory with applications；CHEN Xiang-en（1965-），male，native of Tianshui，Gansu，a professor of Northwest Normal University，M.S.D.，engages in graph theory with applications.